homework 3 writing linear equations applications & linear regression answers

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons

Margin Size

• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

12.3: The Regression Equation

• Last updated
• Save as PDF
• Page ID 23495

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)

( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

\( \newcommand{\Span}{\mathrm{span}}\)

\( \newcommand{\id}{\mathrm{id}}\)

\( \newcommand{\kernel}{\mathrm{null}\,}\)

\( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\)

\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\)

\( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)

\( \newcommand{\vectorA}[1]{\vec{#1}}      % arrow\)

\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}}      % arrow\)

\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vectorC}[1]{\textbf{#1}} \)

\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)

\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)

\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)

Data rarely fit a straight line exactly. Usually, you must be satisfied with rough predictions. Typically, you have a set of data whose scatter plot appears to "fit" a straight line. This is called a Line of Best Fit or Least-Squares Line.

COLLABORATIVE EXERCISE

If you know a person's pinky (smallest) finger length, do you think you could predict that person's height? Collect data from your class (pinky finger length, in inches). The independent variable, \(x\), is pinky finger length and the dependent variable, \(y\), is height. For each set of data, plot the points on graph paper. Make your graph big enough and use a ruler . Then "by eye" draw a line that appears to "fit" the data. For your line, pick two convenient points and use them to find the slope of the line. Find the \(y\)-intercept of the line by extending your line so it crosses the \(y\)-axis. Using the slopes and the \(y\)-intercepts, write your equation of "best fit." Do you think everyone will have the same equation? Why or why not? According to your equation, what is the predicted height for a pinky length of 2.5 inches?

Example \(\PageIndex{1}\)

A random sample of 11 statistics students produced the following data, where \(x\) is the third exam score out of 80, and \(y\) is the final exam score out of 200. Can you predict the final exam score of a random student if you know the third exam score?

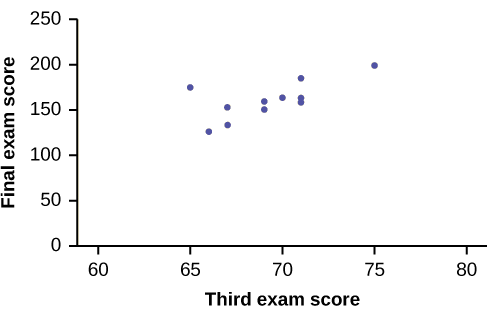
Exercise \(\PageIndex{1}\)

SCUBA divers have maximum dive times they cannot exceed when going to different depths. The data in Table show different depths with the maximum dive times in minutes. Use your calculator to find the least squares regression line and predict the maximum dive time for 110 feet.

\(\hat{y} = 127.24 – 1.11x\)

At 110 feet, a diver could dive for only five minutes.

The third exam score, \(x\), is the independent variable and the final exam score, \(y\), is the dependent variable. We will plot a regression line that best "fits" the data. If each of you were to fit a line "by eye," you would draw different lines. We can use what is called a least-squares regression line to obtain the best fit line.

Consider the following diagram. Each point of data is of the the form (\(x, y\)) and each point of the line of best fit using least-squares linear regression has the form (\(x, \hat{y}\)).

The \(\hat{y}\) is read " \(y\) hat" and is the estimated value of \(y\). It is the value of \(y\) obtained using the regression line. It is not generally equal to \(y\) from data.

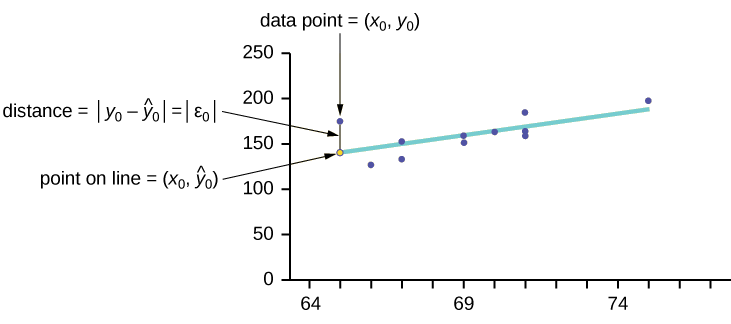
The term \(y_{0} – \hat{y}_{0} = \varepsilon_{0}\) is called the "error" or residual. It is not an error in the sense of a mistake. The absolute value of a residual measures the vertical distance between the actual value of \(y\) and the estimated value of \(y\). In other words, it measures the vertical distance between the actual data point and the predicted point on the line.

If the observed data point lies above the line, the residual is positive, and the line underestimates the actual data value for \(y\). If the observed data point lies below the line, the residual is negative, and the line overestimates that actual data value for \(y\).

In the diagram in Figure, \(y_{0} – \hat{y}_{0} = \varepsilon_{0}\) is the residual for the point shown. Here the point lies above the line and the residual is positive.

\(\varepsilon =\) the Greek letter epsilon

For each data point, you can calculate the residuals or errors, \(y_{i} - \hat{y}_{i} = \varepsilon_{i}\) for \(i = 1, 2, 3, ..., 11\).

Each \(|\varepsilon|\) is a vertical distance.

For the example about the third exam scores and the final exam scores for the 11 statistics students, there are 11 data points. Therefore, there are 11 \(\varepsilon\) values. If you square each \(\varepsilon\) and add, you get

\[(\varepsilon_{1})^{2} + (\varepsilon_{2})^{2} + \dotso + (\varepsilon_{11})^{2} = \sum^{11}_{i = 1} \varepsilon^{2} \label{SSE}\]

Equation\ref{SSE} is called the Sum of Squared Errors (SSE) .

Using calculus, you can determine the values of \(a\) and \(b\) that make the SSE a minimum. When you make the SSE a minimum, you have determined the points that are on the line of best fit. It turns out that the line of best fit has the equation:

\[\hat{y} = a + bx\]

• \(a = \bar{y} - b\bar{x}\) and
• \(b = \dfrac{\sum(x - \bar{x})(y - \bar{y})}{\sum(x - \bar{x})^{2}}\).

The sample means of the \(x\) values and the \(x\) values are \(\bar{x}\) and \(\bar{y}\), respectively. The best fit line always passes through the point \((\bar{x}, \bar{y})\).

The slope \(b\) can be written as \(b = r\left(\dfrac{s_{y}}{s_{x}}\right)\) where \(s_{y} =\) the standard deviation of the \(y\) values and \(s_{x} =\) the standard deviation of the \(x\) values. \(r\) is the correlation coefficient, which is discussed in the next section.

Least Square Criteria for Best Fit

The process of fitting the best-fit line is called linear regression . The idea behind finding the best-fit line is based on the assumption that the data are scattered about a straight line. The criteria for the best fit line is that the sum of the squared errors (SSE) is minimized, that is, made as small as possible. Any other line you might choose would have a higher SSE than the best fit line. This best fit line is called the least-squares regression line .

Computer spreadsheets, statistical software, and many calculators can quickly calculate the best-fit line and create the graphs. The calculations tend to be tedious if done by hand. Instructions to use the TI-83, TI-83+, and TI-84+ calculators to find the best-fit line and create a scatterplot are shown at the end of this section.

THIRD EXAM vs FINAL EXAM EXAMPLE:

The graph of the line of best fit for the third-exam/final-exam example is as follows:

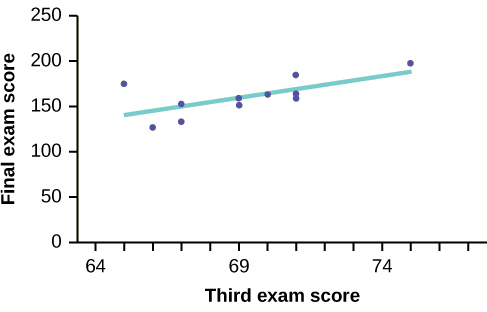
The least squares regression line (best-fit line) for the third-exam/final-exam example has the equation:

\[\hat{y} = -173.51 + 4.83x\]

Remember, it is always important to plot a scatter diagram first. If the scatter plot indicates that there is a linear relationship between the variables, then it is reasonable to use a best fit line to make predictions for \(y\) given \(x\) within the domain of \(x\)-values in the sample data, but not necessarily for x -values outside that domain. You could use the line to predict the final exam score for a student who earned a grade of 73 on the third exam. You should NOT use the line to predict the final exam score for a student who earned a grade of 50 on the third exam, because 50 is not within the domain of the \(x\)-values in the sample data, which are between 65 and 75.

Understanding Slope

The slope of the line, \(b\), describes how changes in the variables are related. It is important to interpret the slope of the line in the context of the situation represented by the data. You should be able to write a sentence interpreting the slope in plain English.

INTERPRETATION OF THE SLOPE: The slope of the best-fit line tells us how the dependent variable (\(y\)) changes for every one unit increase in the independent (\(x\)) variable, on average.

THIRD EXAM vs FINAL EXAM EXAMPLE

Slope: The slope of the line is \(b = 4.83\).

Interpretation: For a one-point increase in the score on the third exam, the final exam score increases by 4.83 points, on average.

USING THE TI-83, 83+, 84, 84+ CALCULATOR

Using the Linear Regression T Test: LinRegTTest

• In the STAT list editor, enter the \(X\) data in list L1 and the Y data in list L2, paired so that the corresponding (\(x,y\)) values are next to each other in the lists. (If a particular pair of values is repeated, enter it as many times as it appears in the data.)
• On the STAT TESTS menu, scroll down with the cursor to select the LinRegTTest. (Be careful to select LinRegTTest, as some calculators may also have a different item called LinRegTInt.)
• On the LinRegTTest input screen enter: Xlist: L1 ; Ylist: L2 ; Freq: 1
• On the next line, at the prompt \(\beta\) or \(\rho\), highlight "\(\neq 0\)" and press ENTER
• Leave the line for "RegEq:" blank
• Highlight Calculate and press ENTER.

The output screen contains a lot of information. For now we will focus on a few items from the output, and will return later to the other items.

The second line says \(y = a + bx\). Scroll down to find the values \(a = -173.513\), and \(b = 4.8273\); the equation of the best fit line is \(\hat{y} = -173.51 + 4.83x\)

The two items at the bottom are \(r_{2} = 0.43969\) and \(r = 0.663\). For now, just note where to find these values; we will discuss them in the next two sections.

Graphing the Scatterplot and Regression Line

• We are assuming your \(X\) data is already entered in list L1 and your \(Y\) data is in list L2
• Press 2nd STATPLOT ENTER to use Plot 1
• On the input screen for PLOT 1, highlight On , and press ENTER
• For TYPE: highlight the very first icon which is the scatterplot and press ENTER
• Indicate Xlist: L1 and Ylist: L2
• For Mark: it does not matter which symbol you highlight.
• Press the ZOOM key and then the number 9 (for menu item "ZoomStat") ; the calculator will fit the window to the data
• To graph the best-fit line, press the "\(Y =\)" key and type the equation \(-173.5 + 4.83X\) into equation Y1. (The \(X\) key is immediately left of the STAT key). Press ZOOM 9 again to graph it.
• Optional: If you want to change the viewing window, press the WINDOW key. Enter your desired window using Xmin, Xmax, Ymin, Ymax

Another way to graph the line after you create a scatter plot is to use LinRegTTest.

• Make sure you have done the scatter plot. Check it on your screen.
• Go to LinRegTTest and enter the lists.
• At RegEq: press VARS and arrow over to Y-VARS. Press 1 for 1:Function. Press 1 for 1:Y1. Then arrow down to Calculate and do the calculation for the line of best fit.
• Press \(Y = (\text{you will see the regression equation})\).
• Press GRAPH. The line will be drawn."

The Correlation Coefficient \(r\)

Besides looking at the scatter plot and seeing that a line seems reasonable, how can you tell if the line is a good predictor? Use the correlation coefficient as another indicator (besides the scatterplot) of the strength of the relationship between \(x\) and \(y\). The correlation coefficient, \(r\) , developed by Karl Pearson in the early 1900s, is numerical and provides a measure of strength and direction of the linear association between the independent variable \(x\) and the dependent variable \(y\).

The correlation coefficient is calculated as

\[r = \dfrac{n \sum(xy) - \left(\sum x\right)\left(\sum y\right)}{\sqrt{\left[n \sum x^{2} - \left(\sum x\right)^{2}\right] \left[n \sum y^{2} - \left(\sum y\right)^{2}\right]}}\]

where \(n =\) the number of data points.

If you suspect a linear relationship between \(x\) and \(y\), then \(r\) can measure how strong the linear relationship is.

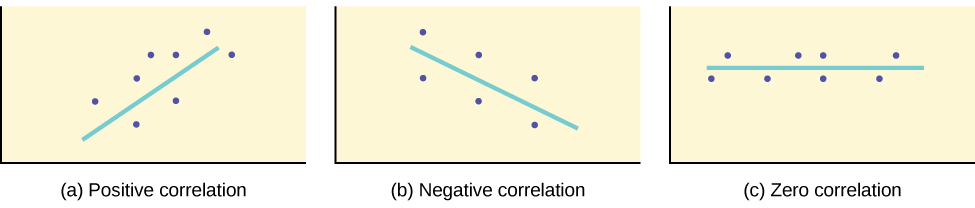
What the VALUE of \(r\) tells us:

• The value of \(r\) is always between –1 and +1: –1 ≤ r ≤ 1.
• The size of the correlation \(r\) indicates the strength of the linear relationship between \(x\) and \(y\). Values of \(r\) close to –1 or to +1 indicate a stronger linear relationship between \(x\) and \(y\).
• If \(r = 0\) there is absolutely no linear relationship between \(x\) and \(y\) (no linear correlation) .
• If \(r = 1\), there is perfect positive correlation. If \(r = -1\), there is perfect negative correlation. In both these cases, all of the original data points lie on a straight line. Of course,in the real world, this will not generally happen.

What the SIGN of \(r\) tells us:

• A positive value of \(r\) means that when \(x\) increases, \(y\) tends to increase and when \(x\) decreases, \(y\) tends to decrease (positive correlation) .
• A negative value of \(r\) means that when \(x\) increases, \(y\) tends to decrease and when \(x\) decreases, \(y\) tends to increase (negative correlation) .
• The sign of \(r\) is the same as the sign of the slope, \(b\), of the best-fit line.

Strong correlation does not suggest that \(x\) causes \(y\) or \(y\) causes \(x\). We say "correlation does not imply causation."

The formula for \(r\) looks formidable. However, computer spreadsheets, statistical software, and many calculators can quickly calculate \(r\). The correlation coefficient \(r\) is the bottom item in the output screens for the LinRegTTest on the TI-83, TI-83+, or TI-84+ calculator (see previous section for instructions).

The Coefficient of Determination

The variable \(r^{2}\) is called the coefficient of determination and is the square of the correlation coefficient, but is usually stated as a percent, rather than in decimal form. It has an interpretation in the context of the data:

• \(r^{2}\), when expressed as a percent, represents the percent of variation in the dependent (predicted) variable \(y\) that can be explained by variation in the independent (explanatory) variable \(x\) using the regression (best-fit) line.
• \(1 - r^{2}\), when expressed as a percentage, represents the percent of variation in \(y\) that is NOT explained by variation in \(x\) using the regression line. This can be seen as the scattering of the observed data points about the regression line.

Consider the third exam/final exam example introduced in the previous section

• The line of best fit is: \(\hat{y} = -173.51 + 4.83x\)
• The correlation coefficient is \(r = 0.6631\)
• The coefficient of determination is \(r^{2} = 0.6631^{2} = 0.4397\)
• Interpretation of \(r^{2}\) in the context of this example:
• Approximately 44% of the variation (0.4397 is approximately 0.44) in the final-exam grades can be explained by the variation in the grades on the third exam, using the best-fit regression line.
• Therefore, approximately 56% of the variation (\(1 - 0.44 = 0.56\)) in the final exam grades can NOT be explained by the variation in the grades on the third exam, using the best-fit regression line. (This is seen as the scattering of the points about the line.)

A regression line, or a line of best fit, can be drawn on a scatter plot and used to predict outcomes for the \(x\) and \(y\) variables in a given data set or sample data. There are several ways to find a regression line, but usually the least-squares regression line is used because it creates a uniform line. Residuals, also called “errors,” measure the distance from the actual value of \(y\) and the estimated value of \(y\). The Sum of Squared Errors, when set to its minimum, calculates the points on the line of best fit. Regression lines can be used to predict values within the given set of data, but should not be used to make predictions for values outside the set of data.

The correlation coefficient \(r\) measures the strength of the linear association between \(x\) and \(y\). The variable \(r\) has to be between –1 and +1. When \(r\) is positive, the \(x\) and \(y\) will tend to increase and decrease together. When \(r\) is negative, \(x\) will increase and \(y\) will decrease, or the opposite, \(x\) will decrease and \(y\) will increase. The coefficient of determination \(r^{2}\), is equal to the square of the correlation coefficient. When expressed as a percent, \(r^{2}\) represents the percent of variation in the dependent variable \(y\) that can be explained by variation in the independent variable \(x\) using the regression line.

\[r = \dfrac{n \sum xy - \left(\sum x\right) \left(\sum y\right)}{\sqrt{\left[n \sum x^{2} - \left(\sum x\right)^{2}\right] \left[n \sum y^{2} - \left(\sum y\right)^{2}\right]}}\]

Unit 2: Linear Functions

Answer keys, lf1: i can write a linear equation from a situation or pattern.

LF1 Writing Linear Equations

Independent and Dependent Variables

Linear Intro

Writing equations, extra resources.

LF1 Skill Sheets

LF2: I use a linear equation to answer a question about a situation.

LF2 Using Linear Equations

Using equations.

LF2 Skill Sheets

LF3: I can write a linear equation from a table.

LF3 Equations from Tables

LF3 Skill Sheets

LF4: I can solve for "b."

LF4 Solving for "b"

Solving for "b".

LF4 Skill Sheets

LF5: I can write a linear equation from a graph.

LF5 Equations from Graphs

Horizontal and Vertical Lines

Equation from graph.

LF5 Skill Sheets

LF6: I can write a linear equation from two points.

LF6 Slope Formula

LF6 Skill Sheets

LF7: I can graph a line written in slope-intercept form: y=mx+b.

LF7 Graphing Lines

Graphing lines.

LF7 Skill Sheets

LF8: I can write and graph a line written in point-slope form: (y - y1) = m(x - x2).

LF8 Point-Slope Form

Point-slope form.

LF8 Skill Sheets

LF9: I can graph a line written in Standard Form: Ax + By = C.

LF9 Standard Form

Standard form, word problems.

All three forms

Google Slides Graphing Practice

LF9 Skill Sheets

LF10: I can transform equations between all three forms.

LF10 Transforming Between Forms

Transforming forms.

LF10 Skill Sheets

Previous Assessments (2018/2019)

Want to create or adapt books like this? Learn more about how Pressbooks supports open publishing practices.

Chapter 3: Graphing

3.4 Graphing Linear Equations

There are two common procedures that are used to draw the line represented by a linear equation. The first one is called the slope-intercept method and involves using the slope and intercept given in the equation.

If the equation is given in the form [latex]y = mx + b[/latex], then [latex]m[/latex] gives the rise over run value and the value [latex]b[/latex] gives the point where the line crosses the [latex]y[/latex]-axis, also known as the [latex]y[/latex]-intercept.

Example 3.4.1

Given the following equations, identify the slope and the [latex]y[/latex]-intercept.

• [latex]\begin{array}{lll} y = 2x - 3\hspace{0.14in} & \text{Slope }(m)=2\hspace{0.1in}&y\text{-intercept } (b)=-3 \end{array}[/latex]
• [latex]\begin{array}{lll} y = \dfrac{1}{2}x - 1\hspace{0.08in} & \text{Slope }(m)=\dfrac{1}{2}\hspace{0.1in}&y\text{-intercept } (b)=-1 \end{array}[/latex]
• [latex]\begin{array}{lll} y = -3x + 4 & \text{Slope }(m)=-3 &y\text{-intercept } (b)=4 \end{array}[/latex]
• [latex]\begin{array}{lll} y = \dfrac{2}{3}x\hspace{0.34in} & \text{Slope }(m)=\dfrac{2}{3}\hspace{0.1in} &y\text{-intercept } (b)=0 \end{array}[/latex]

When graphing a linear equation using the slope-intercept method, start by using the value given for the [latex]y[/latex]-intercept. After this point is marked, then identify other points using the slope.

This is shown in the following example.

Example 3.4.2

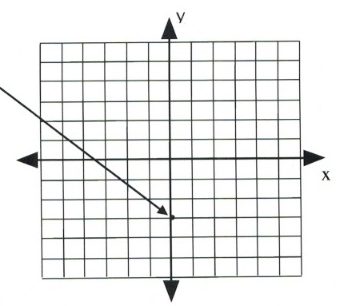
Graph the equation [latex]y = 2x - 3[/latex].

First, place a dot on the [latex]y[/latex]-intercept, [latex]y = -3[/latex], which is placed on the coordinate [latex](0, -3).[/latex]

Now, place the next dot using the slope of 2.

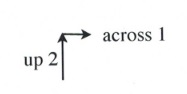
A slope of 2 means that the line rises 2 for every 1 across.

Simply, [latex]m = 2[/latex] is the same as [latex]m = \dfrac{2}{1}[/latex], where [latex]\Delta y = 2[/latex] and [latex]\Delta x = 1[/latex].

Placing these points on the graph becomes a simple counting exercise, which is done as follows:

Once several dots have been drawn, draw a line through them, like so:

Note that dots can also be drawn in the reverse of what has been drawn here.

Slope is 2 when rise over run is [latex]\dfrac{2}{1}[/latex] or [latex]\dfrac{-2}{-1}[/latex], which would be drawn as follows:

Example 3.4.3

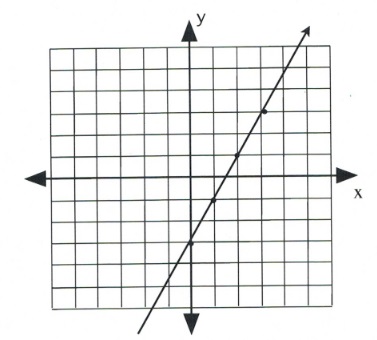
Graph the equation [latex]y = \dfrac{2}{3}x[/latex].

First, place a dot on the [latex]y[/latex]-intercept, [latex](0, 0)[/latex].

Now, place the dots according to the slope, [latex]\dfrac{2}{3}[/latex].

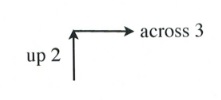
This will generate the following set of dots on the graph. All that remains is to draw a line through the dots.

The second method of drawing lines represented by linear equations and functions is to identify the two intercepts of the linear equation. Specifically, find [latex]x[/latex] when [latex]y = 0[/latex] and find [latex]y[/latex] when [latex]x = 0[/latex].

Example 3.4.4

Graph the equation [latex]2x + y = 6[/latex].

To find the first coordinate, choose [latex]x = 0[/latex].

This yields:

[latex]\begin{array}{lllll} 2(0)&+&y&=&6 \\ &&y&=&6 \end{array}[/latex]

Coordinate is [latex](0, 6)[/latex].

Now choose [latex]y = 0[/latex].

[latex]\begin{array}{llrll} 2x&+&0&=&6 \\ &&2x&=&6 \\ &&x&=&\frac{6}{2} \text{ or } 3 \end{array}[/latex]

Coordinate is [latex](3, 0)[/latex].

Draw these coordinates on the graph and draw a line through them.

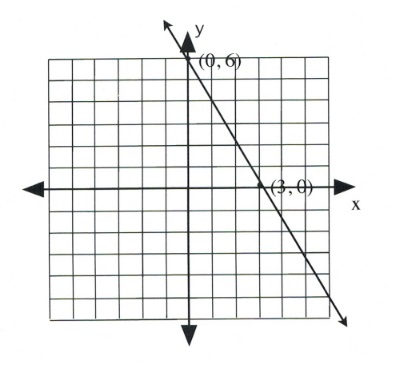
Example 3.4.5

Graph the equation [latex]x + 2y = 4[/latex].

[latex]\begin{array}{llrll} (0)&+&2y&=&4 \\ &&y&=&\frac{4}{2} \text{ or } 2 \end{array}[/latex]

Coordinate is [latex](0, 2)[/latex].

[latex]\begin{array}{llrll} x&+&2(0)&=&4 \\ &&x&=&4 \end{array}[/latex]

Coordinate is [latex](4, 0)[/latex].

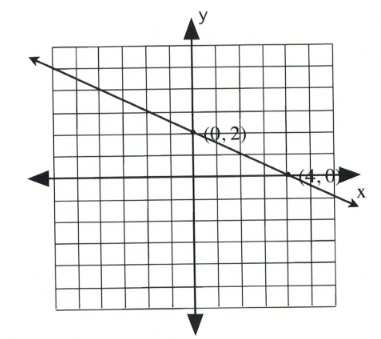
Example 3.4.6

Graph the equation [latex]2x + y = 0[/latex].

[latex]\begin{array}{llrll} 2(0)&+&y&=&0 \\ &&y&=&0 \end{array}[/latex]

Coordinate is [latex](0, 0)[/latex].

Since the intercept is [latex](0, 0)[/latex], finding the other intercept yields the same coordinate. In this case, choose any value of convenience.

Choose [latex]x = 2[/latex].

[latex]\begin{array}{rlrlr} 2(2)&+&y&=&0 \\ 4&+&y&=&0 \\ -4&&&&-4 \\ \hline &&y&=&-4 \end{array}[/latex]

Coordinate is [latex](2, -4)[/latex].

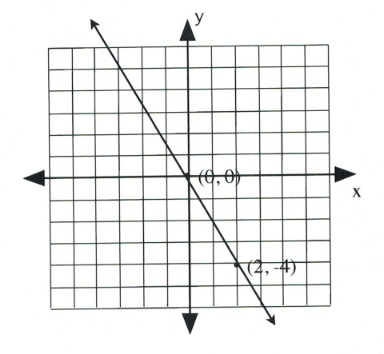
For questions 1 to 10, sketch each linear equation using the slope-intercept method.

• [latex]y = -\dfrac{1}{4}x - 3[/latex]
• [latex]y = \dfrac{3}{2}x - 1[/latex]
• [latex]y = -\dfrac{5}{4}x - 4[/latex]
• [latex]y = -\dfrac{3}{5}x + 1[/latex]
• [latex]y = -\dfrac{4}{3}x + 2[/latex]
• [latex]y = \dfrac{5}{3}x + 4[/latex]
• [latex]y = \dfrac{3}{2}x - 5[/latex]
• [latex]y = -\dfrac{2}{3}x - 2[/latex]
• [latex]y = -\dfrac{4}{5}x - 3[/latex]
• [latex]y = \dfrac{1}{2}x[/latex]

For questions 11 to 20, sketch each linear equation using the [latex]x\text{-}[/latex] and [latex]y[/latex]-intercepts.

• [latex]x + 4y = -4[/latex]
• [latex]2x - y = 2[/latex]
• [latex]2x + y = 4[/latex]
• [latex]3x + 4y = 12[/latex]
• [latex]4x + 3y = -12[/latex]
• [latex]x + y = -5[/latex]
• [latex]3x + 2y = 6[/latex]
• [latex]x - y = -2[/latex]
• [latex]4x - y = -4[/latex]

For questions 21 to 28, sketch each linear equation using any method.

• [latex]y = -\dfrac{1}{2}x + 3[/latex]
• [latex]y = 2x - 1[/latex]
• [latex]y = -\dfrac{5}{4}x[/latex]
• [latex]y = -3x + 2[/latex]
• [latex]y = -\dfrac{3}{2}x + 1[/latex]
• [latex]y = \dfrac{1}{3}x - 3[/latex]
• [latex]y = \dfrac{3}{2}x + 2[/latex]
• [latex]y = 2x - 2[/latex]

For questions 29 to 40, reduce and sketch each linear equation using any method.

• [latex]y + 3 = -\dfrac{4}{5}x + 3[/latex]
• [latex]y - 4 = \dfrac{1}{2}x[/latex]
• [latex]x + 5y = -3 + 2y[/latex]
• [latex]3x - y = 4 + x - 2y[/latex]
• [latex]4x + 3y = 5 (x + y)[/latex]
• [latex]3x + 4y = 12 - 2y[/latex]
• [latex]2x - y = 2 - y \text{ (tricky)}[/latex]
• [latex]7x + 3y = 2(2x + 2y) + 6[/latex]
• [latex]x + y = -2x + 3[/latex]
• [latex]3x + 4y = 3y + 6[/latex]
• [latex]2(x + y) = -3(x + y) + 5[/latex]
• [latex]9x - y = 4x + 5[/latex]

Answer Key 3.4

Intermediate Algebra Copyright © 2020 by Terrance Berg is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License , except where otherwise noted.

Share This Book

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons

Margin Size

• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

2.4: Graphing Linear Equations- Answers to the Homework Exercises

• Last updated
• Save as PDF
• Page ID 45036

• Darlene Diaz
• Santiago Canyon College via ASCCC Open Educational Resources Initiative

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)

( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

\( \newcommand{\Span}{\mathrm{span}}\)

\( \newcommand{\id}{\mathrm{id}}\)

\( \newcommand{\kernel}{\mathrm{null}\,}\)

\( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\)

\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\)

\( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)

\( \newcommand{\vectorA}[1]{\vec{#1}}      % arrow\)

\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}}      % arrow\)

\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vectorC}[1]{\textbf{#1}} \)

\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)

\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)

\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)

Graphing and Slope

• \(\frac{1}{3}\)
• \(\frac{4}{3}\)
• \(\frac{1}{2}\)
• \(-\frac{1}{3}\)
• \(\frac{16}{7}\)
• \(-\frac{7}{17}\)
• \(\frac{1}{16}\)
• \(\frac{24}{11}\)
• \(x=\frac{23}{6}\)
• \(y=-\frac{29}{6}\)

Equations of Lines

• \(y=-\frac{3}{4}x-1\)
• \(y = −6x + 4\)
• \(y = − \frac{1}{4} x + 3\)
• \(y = \frac{1}{3} x + 3\)
• \(y = −3x + 5\)
• \(y = − \frac{1}{10} x − \frac{37}{10}\)
• \(y = \frac{7x}{3} − 8\)
• \(y = −4x + 3\)
• \(y = \frac{1}{10} x − \frac{3}{10}\)
• \(y = − \frac{4}{7} x + 4\)
• \(y=\frac{5}{2}x\)

• \(y − (−5) = 9(x − (−1))\)
• \(y − (−2) = −3(x − 0)\)
• \(y − (−3) = \frac{1}{5} (x − (−5))\)
• \(y − 2 = 0(x − 1)\)
• \(y − (−2) = −2(x − 2)\)
• \(y − 1 = 4(x − (−1))\)
• \(y − (−4) = − \frac{2}{3} (x − (−1))\)
• \(y = − \frac{3}{5} x + 2\)
• \(y = − \frac{3}{2} x + 4\)
• \(y = x − 4\)
• \(y = − \frac{1}{2} x\)
• \(y = − \frac{2}{3} x − \frac{10}{3}\)
• \(y = − \frac{5}{2} x − 5\)
• \(y = −3\)
• \(y − 3 = −2(x + 4)\)
• \(y + 2 = \frac{3}{2} (x + 4)\)
• \(y + 3 = − \frac{8}{7} (x − 3)\)
• \(y − 5 = − \frac{1}{8} (x + 4)\)
• \(y + 4 = −(x + 1)\)
• \(y = − \frac{8}{7} x − \frac{5}{7}\)
• \(y = −x + 2\)
• \(y = − \frac{1}{10} x − \frac{3}{2}\)
• \(y=\frac{1}{3}x+1\)

Parallel and Perpendicular Lines

• \(m_{||} = 2\)
• \(m_{||} = 1\)
• \(m_{||} = − \frac{2}{3}\)
• \(m_{||} = \frac{6}{5}\)
• \(m_{⊥} = 0\)
• \(m_{⊥} = −3\)
• \(m_{⊥} = 2\)
• \(m_{⊥} = − \frac{1}{3}\)
• \(y − 4 = \frac{9}{2} (x − 3)\)
• \(y − 3 = \frac{7}{5} (x − 2)\)
• \(y + 5 = −(x − 1)\)
• \(y − 2 = \frac{1}{5} (x − 5)\)
• \(y − 2 = − \frac{1}{4} (x − 4)\)
• \(y + 2 = −3(x − 2)\)
• \(y = −2x + 5\)
• \(y = − \frac{4}{3} x − 3\)
• \(y = − \frac{1}{2} x − 3\)
• \(y = − \frac{1}{2} x − 2\)
• \(y = x − 1\)
• \(y=-2x+5\)

Linear Functions and Systems (Algebra 2 - Unit 2) | All Things Algebra®

• Google Apps™

What educators are saying

Also included in.

Description

This Linear Functions and Systems Unit Bundle includes guided notes, homework assignments, two quizzes, a study guide and a unit test that cover the following topics:

• Domain and Range of a Relation

• Relations vs. Functions

• Evaluating Functions

• Linear Equations: Standard Form vs. Slope-Intercept Form

• Graphing by Slope-Intercept Form

• Graphing by x- and y-intercepts

• Vertical and Horizontal Lines

• Parallel vs. Perpendicular Lines

• Writing Linear Equations: Given Point and Slope or Two Points

• Linear Equation Applications

• Linear Regression

• Solving Systems of Equations by Graphing, Substitution, and Elimination

• Systems of Equations Applications

• Solving Systems with Three Variables

• Graphing Linear Inequalities

• Graphing Systems of Linear Inequalities

• Linear Inequalities & Systems of Inequalities Applications

• Linear Programming

ADDITIONAL COMPONENTS INCLUDED:

(1) Links to Instructional Videos: Links to videos of each lesson in the unit are included. Videos were created by fellow teachers for their students using the guided notes and shared in March 2020 when schools closed with no notice.  Please watch through first before sharing with your students. Many teachers still use these in emergency substitute situations. (2) Editable Assessments: Editable versions of each quiz and the unit test are included. PowerPoint is required to edit these files. Individual problems can be changed to create multiple versions of the assessment. The layout of the assessment itself is not editable. If your Equation Editor is incompatible with mine (I use MathType), simply delete my equation and insert your own.

(3) Google Slides Version of the PDF: The second page of the Video links document contains a link to a Google Slides version of the PDF. Each page is set to the background in Google Slides. There are no text boxes;  this is the PDF in Google Slides.  I am unable to do text boxes at this time but hope this saves you a step if you wish to use it in Slides instead! 

This resource is included in the following bundle(s):

Algebra 2 Curriculum

More Algebra 2 Units:

Unit 1 – Equations and Inequalities

Unit 3 – Parent Functions and Transformations

Unit 4 – Quadratic Equations and Complex Numbers

Unit 5 – Polynomial Functions

Unit 6 – Radical Functions

Unit 7 – Exponential and Logarithmic Functions

Unit 8 – Rational Functions

Unit 9 – Conic Sections

Unit 10 – Sequences and Series

Unit 11 – Probability and Statistics

Unit 12 – Trigonometry

LICENSING TERMS: This purchase includes a license for one teacher only for personal use in their classroom. Licenses are non-transferable , meaning they can not be passed from one teacher to another. No part of this resource is to be shared with colleagues or used by an entire grade level, school, or district without purchasing the proper number of licenses. If you are a coach, principal, or district interested in transferable licenses to accommodate yearly staff changes, please contact me for a quote at [email protected].

COPYRIGHT TERMS: This resource may not be uploaded to the internet in any form, including classroom/personal websites or network drives, unless the site is password protected and can only be accessed by students.

© All Things Algebra (Gina Wilson), 2012-present

Questions & Answers

All things algebra.

• We're hiring
• Help & FAQ
• Privacy policy
• Student privacy
• Terms of service
• Tell us what you think

What if I’m unsatisfied with an essay your paper service delivers?

Customer Reviews

Finished Papers

Write My Essay Service Helps You Succeed!

Being a legit essay service requires giving customers a personalized approach and quality assistance. We take pride in our flexible pricing system which allows you to get a personalized piece for cheap and in time for your deadlines. Moreover, we adhere to your specific requirements and craft your work from scratch. No plagiarized content ever exits our professional writing service as we care. about our reputation. Want to receive good grades hassle-free and still have free time? Just shoot us a "help me with essay" request and we'll get straight to work.

260 King Street, San Francisco

Updated Courtyard facing Unit at the Beacon! This newly remodeled…

1035 Natoma Street, San Francisco

This exquisite Edwardian single-family house has a 1344 Sqft main…

Leave a Reply Cancel reply

Your email address will not be published. Required fields are marked *

Save my name, email, and website in this browser for the next time I comment.

Finished Papers

Will I get caught if I buy an essay?

The most popular question from clients and people on the forums is how not to get caught up in the fact that you bought an essay, and did not write it yourself. Students are very afraid that they will be exposed and expelled from the university or they will simply lose their money, because they will have to redo the work themselves.

If you've chosen a good online research and essay writing service, then you don't have to worry. The writers from the firm conduct their own exploratory research, add scientific facts and back it up with the personal knowledge. None of them copy information from the Internet or steal ready-made articles. Even if this is not enough for the client, he can personally go to the anti-plagiarism website and check the finished document. Of course, the staff of the sites themselves carry out such checks, but no one can forbid you to make sure of the uniqueness of the article for yourself.

Thanks to the privacy policy on web platforms, no one will disclose your personal data and transfer to third parties. You are completely safe from start to finish.

• Article Sample
• Terms & Conditions
• Privacy Policy