9 6 problem solving geometric probability answers

Geometric Probability

Geometric probability is the visual representation of probability. Many of the probabilities are continuous and for these probabilities, it is easy to represent as a geometric probability. The area of the geometric figure is used to compute the probabilities. The geometric probability is the probable area divided by the entire area.

Let us learn more about geometric probability and the representation of geometric probability with the help of examples, FAQs.

What Is Geometric Probability?

Geometric probability is the representation of probability geometrically. The probabilities which are non-discrete or are continuous are represented across a number line or across a two-dimensional plane. The experiment having numerous probability outcomes are often represented as a geometric probability.

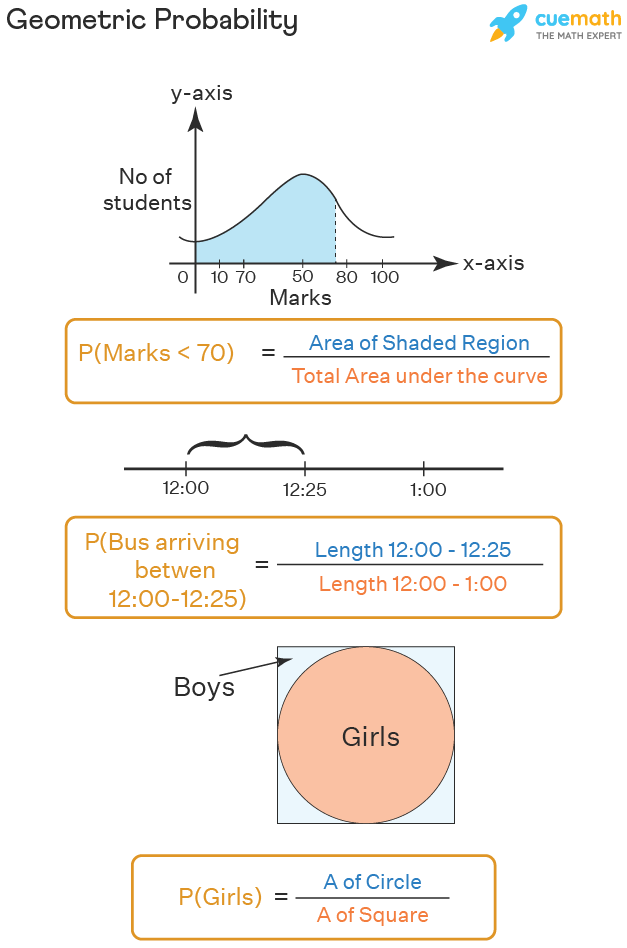
Probability is the mathematical way of calculating how likely a particular event may happen. Probability values always lie between 0 and 1,and sometimes they are also expressed as a percentage. The geometric probability is the representation of the probability as a form of a geometric figure such that the happening of an event is shaded as part of the area of the entire figure. We can assume geometric probability as a dartboard and the probability of hitting a particular area of the dartboard.

For calculation of geometric probability, we are only required to know the expected area where we want to hit with reference to the total area. Geometric probability is obtained by dividing the expected area by the total area.

Geometric Probability = Probable Area/Total Area

Geometric probability is also used to sometimes represent the different outcome probabilities at the same time. A few quick examples of geometric probability are as follows.

• The probability of the arrival of a train across a time period is a continuous probability, which can be represented as a geometric probability.
• In a class, the probability of a number of students gaining 65% or more marks can be represented as a geometric probability. This can be represented as a normal distribution, and the probability region can be shaded.
• Among a group of people, 30% drink tea, 40% drink coffee, and the remaining 30% drink soft drinks. This can be represented as a shaded region in a pi diagram.
• The probability of incidence of covid-19 among the population can be graphically represented as a geometric probability.

Representation of Geometric Probability

The geometric probabilities can be represented in a single dimension, two-dimensions, or n-dimensions, and can be represented as an area of the shaded probable region, with reference to the area of the entire region.

Number Line: The continuous probabilities are marked as a point on the number lines, and the length of the line from the starting point divided by the entire length of the line gives the probability answer.

Two Dimensional Plane: The geometric probability can be represented in the two-dimensional graph as a normal curve, as a pi diagram, or any other geometric shape. For the representation of the probability of a single event we use the normal curve, and represent the probability as the part of the area of the normal curve. And for representing multiple probabilities we use a Pi diagram or any other diagram. Further, we can represent geometric probability in higher dimensions also.

Percentage Format: Geometri probability is numerically represented as a percentage. The percentage value represents the happening of the event or the area of the geometric figure. 100% refers to the entire shaded image and it means the sure happening of the event. A 50% is represented as a half-shaded region and is equal to half of the chances of happening of an event.

☛ Related Topics

• Discrete Probability Distribution
• Probability Theory
• Events in Probability
• Theoretical Probability
• Probability Distribution
• Probability Tree Diagram

Examples on Geometric Probability

Example 1: Find the geometric probability of selecting a girl from a class, if the girls of the class are represented by a circle of radius 3.5 cms, and the entire class of students is represented by a larger square of side 8 cms.

Given that the girls represent the circle if radius 3.5cms, and the entire class of students represent a square of side 8 cms.

Area of the circle = πr 2 = 22/7 × 3.5 × 3.5 = 38.5

Area of the square = s 2 = 8 × 8 = 64

Probability of selecting the girl = Area of Circle/Area of Square

Probability of selecting the girl = 38.5/64

Therefore the probability of selecting the girl from the class of students is 38.5/64.

Example 2: Find the geometric probability of the number of students who can speak English, if the people are represented s sectors in a circle, and the English-speaking people represent a sector of 120°.

The number of people who speak English is represented by a sector of angle 120°, and the total number of students of the class are represented by the entire circle, which is an angle of 360°.

Probability of people speaking English = Area of sector/Area of circle = Angle of the sector/Complete angle

Probability of people speaking English = 120°/360° = 1/3

Therefore the probability of people speaking English language is 1/3.

go to slide go to slide

Book a Free Trial Class

Practice Questions on Geometric Probability

Faqs on geometric probability, what is geometric probability in maths.

Geometric probability is the geometric or visual representation of probability in one, two or n-dimensional framework. The experiment having numerous probability outcomes are often represented as a geometric probability. For calculation of geometric probability, we are only required to know the expected area where we want to hit with reference to the total area. Geometric probability is obtained by dividing the expected area by the total area.

Where Do We Use Geometric Probability?

The geometric probabilities are used if the range of probabilities is huge and it is difficult to represent it with a simple value. The geometric quantities of length, area, angle are used to express the probabilities of events.

What Are The Formulas Of Geometric Probability?

The formula of geometric probability is the expected area divided by the total area. We have Geometric Probability = Probable Area/Total Area . Also sometimes in place of area, we can also use the length, angle, or any other geometric quantity.

What Are The Examples Of Geometric Probability?

The examples of geometric probability include events that have a range of probabilities such as the probability of arrival of a bus across a time period. Also simple probabilities with multiple events can be represented as a geometric probability. If a party has people drinking tea, coffee, soft drink, milkshake, water, soda lime, then the probabilities can be easily represented using geometric probability.

What Is The Difference Between Geometric Probability And Discrete Probability?

The geometric probability is different from discrete probability, as the discrete probability has countable events which can be easily computed. The probabilities having continuous probabilities cannot be easily calculated and here we can use geometric probability. Probabilities involving dice, playing cards, coins are all simple examples of discrete probability, but probabilities involving student with a performance range, probabilities with time range can be represented using geometric probability.

Reset password New user? Sign up

Existing user? Log in

Geometric Probability

Already have an account? Log in here.

Recommended Course

Applied probability.

A framework for understanding the world around us, from sports to science.

• Sharky Kesa
• Mahindra Jain
• A Former Brilliant Member
• Samarpit Swain

Geometric probability is a tool to deal with the problem of infinite outcomes by measuring the number of outcomes geometrically, in terms of length, area, or volume. In basic probability, we usually encounter problems that are "discrete" (e.g. the outcome of a dice roll; see probability by outcomes for more). However, some of the most interesting problems involve "continuous" variables (e.g., the arrival time of your bus).

Dealing with continuous variables can be tricky, but geometric probability provides a useful approach by allowing us to transform probability problems into geometry problems. If this sounds surprising, take a look at the following problem:

Your bus is coming at a random time between 12 pm and 1 pm. If you show up at 12:30 pm, how likely are you to catch the bus?

Intuitively, the answer seems to be \(\frac{1} {2} \). We can show this geometrically by considering a point chosen randomly on a 1-dimensional number line: the length of the number line between 12:30 pm and 1 pm is equal to the length from 12 pm to 12:30 pm.

While this example is fairly straightforward, many complicated problems can be solved simply by using geometric probability. On this page, we will start with 1D examples, which are the simplest and easy to understand and then work our way up to 2D, 3D, and higher dimensions.

Introduction

1-dimensional geometric probability, 2-dimensional geometric probability, 3-dimensional geometric probability, applications, extra challenges.

One of the main ideas in probability is to count the number of equally likely "desired" outcomes, and then divide that by the number of equally likely total outcomes:

\[ P(X) = \frac{\mbox{desired outcomes}}{\mbox{total outcomes}} .\]

However, when a variable is continuous , it becomes impossible to "count" the outcomes in the traditional sense. For example, if \(X\) is a random real number between 0 and 1, it could be \(0.2\) or \(0.53\) or \(0.434662565465465\) or even something irrational like \(\frac{\pi}{4}.\) It is clear that there are infinite outcomes if we count in the traditional sense.

Let's look more at the situation where \(X\) is a random real number, as mentioned in the Introduction section.

\(X\) is a random real number between 0 and 3. What is the probability \(X\) is closer to 0 than it is to 1? Since there are infinitely many possible outcomes for the value of \(X,\) we will take the equally likely outcomes as random points along the number line from 0 to 3. It’s easy to see that \(X\) will be closer to 0 than it is to 1 if \(X<0.5.\) Probability line Now, we can use the measures (lengths, in this 1D case) of our possible outcomes and apply the usual probability formula. Here, \[P(X\text{ is closer to 0 than to 1}) = \frac{\mbox{length of segment where }0<X<0.5}{\mbox{length of segment where }0<X<3} = \frac{0.5}{3} = \frac{1}{6} \approx 17\%.\ _\square\]

To reiterate, the core idea in one-dimensional (1D) geometric probability is translating a probability question into a geometry problem on a number line, where we measure outcomes with length . To make sure you've got this concept down, try this problem related to rounding errors:

A number is uniformly chosen from \( [0.15, 0.25] \). It was rounded to two decimal places and then to one decimal place. The probability that the final value is \( 0.2 \) is \( X \% \). What is \(X?\)

Assumption: Use rounding "half away from zero". That is, if the number is equally far from the two closest numbers, choose the one away from zero. For example, 2.5 is equally far from 2 and 3, so round 2.5 to 3.

The reason as to why this works is a more advanced topic, which deals with the idea of measure theory . Measure theory gives a rigorous framework for probability theory, including probabilities on finite sets. Measure theory is also the key idea behind integration in calculus, and can be used to find integrals of functions that seem non-integrable using “standard” methods. These two ideas are not unrelated, as at a fundamental level, probability theory is just a special case of integration.

We will do a few more examples on working with geometric probabilities in higher dimensions to get a better feel for how to work with the concept. It is often helpful to use a figure to help with understanding and solving these types of problems.

Many probability problems include more than one variable, so 1D geometric probability won't be enough. For problems with two variables, it is often helpful to transform them into 2D geometric probability questions, where the outcomes are measured by area :

\[P(X) = \dfrac{\text{area of desired outcomes}}{\text{area of total outcomes}}.\]

This is most easily understood when the problem at hand is explicitly a 2D geometry problem:

A dart is thrown at a circular dartboard such that it will land randomly over the area of the dartboard. What is the probability that it lands closer to the center than to the edge? The set of outcomes are all of the points on the dartboard, which make up an area of \(\pi r^2\) where \(r\) is the radius of the circle. The points that are closer to the center than to the edge are those that lie within the circle of radius \(\frac{r}{2}\) around the center, so the area of the "success" outcomes is \(\pi \left(\frac{r}{2}\right)^2 = \frac{\pi r^2}{4}.\) Thus, \[P(\text{closer to center than edge}) = \dfrac{\text{area of desired outcomes}}{\text{area of total outcomes}} = \frac{\frac{\pi r^2}{4}}{\pi r^2} = \frac{1}{4} = 25\%.\ _\square\]

A square \( S \) has side length 30. A standard 20-sided die is rolled, and a square \( T \) is constructed inside \( S \) with side length equal to the roll. Then, a dart is thrown and lands randomly somewhere inside square \( S \). What is the probability that the dart also lands inside square \( T ?\) Suppose the die rolls \( i \). Then the probability that the dart will land inside square \( T \) is the ratio of the area of square \( T \) to the area of square \( S \). This is \( \frac{i^2}{900} \). For each \( i \), the probability that the die will roll \( i \) is \( \frac{1}{20}, \) so the probability that the dart lands inside \( T \) will be \[ \sum\limits_{i=1}^{20} \frac{1}{20}\cdot \frac{i^2}{900} = \frac{1}{20} \cdot \frac{20 \times 21 \times 41}{900 \times 6} = \frac{287}{1800} . \ _\square\]

The difficulty associated with geometric probability usually comes from one of two areas: the first is finding a good way to model the problem geometrically, and the second is in trying to determine the areas/volumes of particular regions in order to calculate the relative probabilities. As in finite probability, it is sometimes simpler to find the probability of the complement.

To make sure you've got down the basic ideas of 2D geometric probability, try this similar question. Note that many 2D geometry problems, such as the one below, use the ideas of composite figures. If you are not familiar with that concept, you may want to take a look at composite figures first.

The dartboard above is made up of three concentric circles with radii \(1, 3,\) and \(5.\) Assuming that a dart thrown will land randomly on the dartboard, what is the probability that it lands in the green region?

However, one of the most powerful uses of geometric probability is applying it to problems that are not inherently geometric. Identifying when and how to use geometric probability is never obvious, but a good sign is that you are dealing with probabilities in a situation with continuous variables. Let's take a look at a modified example of the bus problem mentioned at the beginning of this wiki.

Both the bus and you get to the bus stop at random times between 12 pm and 1 pm. When the bus arrives, it waits for 5 minutes before leaving. When you arrive, you wait for 20 minutes before leaving if the bus doesn't come. What is the probability that you catch the bus? We have two continuous variables here: \(b,\) the time in minutes past 12 pm that the bus arrives, and \(y,\) the time in minutes past 12 pm that you arrive. Since there are 2 independent variables, we will convert this into a 2-dimensional geometry problem. Specifically, we can think of the set of all outcomes as the points in a square: Then, we need to determine the region of "success"; that is, the points where we catch the bus. Since the bus will wait for 5 minutes, you need to arrive within 5 minutes of the bus' arrival, or \(y \le b+5:\) However, you only wait for 20 minutes, so you can't arrive more than 20 minutes before the bus, so \(y \ge b-20:\) Combining our two conditions, we have a region of success as shown below: Now, we just need to find the area of this success region. A simple method is to find the area of the non-success region, and then subtract that from the total area: Thus, the probability of catching the bus is \[P(\text{catching the bus}) = \dfrac{\text{area of desired outcomes}}{\text{area of total outcomes}} = \frac{60^2 - \frac{55^2}{2}-\frac{40^2}{2}}{60^2} = \frac{103}{288} \approx 36\%.\ _\square\]

Now that we have changed our problem into a geometric one, we can easily answer other questions about the situation such as the following:

1) What is the probability that the bus does not have to wait for you? 2) What is the probability that you had to wait less than 10 minutes, given that you were able to catch the bus? 3) What is the probability that the bus came and went before you, given that you were not able to board the bus?

To practice these ideas, let's try a similar question:

Dave and Kathy both arrive at Pizza Palace at two random times between 10:00 p.m. and midnight. They agree to wait exactly 15 minutes for each other to arrive before leaving. What is the probability that Dave and Kathy see each other?

If the probability is \( \frac ab\) for coprime positive integers, give the answer as \(a+b\).

You have many chocolate bars of unit length and start breaking each of them into 3 pieces by randomly choosing two points on the bar. What are the average lengths of the shortest, medium, and longest pieces?

If the product of these averages can be expressed as \( \frac pq\), where \(p\) and \(q\) are coprime positive integers, give your answer as \(p+ q\).

At this point, you can probably guess where this is headed! 3D geometric probability is when we are dealing with 3 continuous variables, and we measure the volume of the various outcomes; that is,

\[P(X) = \dfrac{\text{volume of desired outcomes}}{\text{volume of total outcomes}}.\]

To get started, let's look at an example which is analogous to the first problem we solved in the 2D geometric probability section.

An atom is inside a sphere and it is equally likely to be anywhere within the sphere. What is the probability that it lands closer to the center of the sphere than the outside? The set of outcomes are all of the points in the sphere, which make up a volume of \(\frac{4\pi}{3} r^3\) where \(r\) is the radius of the sphere. The points that are closer to the center than to the edge are those that lie within the sphere of radius \(\frac{r}{2}\) around the center, so the volume of the "success" outcomes is \(\frac{4\pi}{3} \left(\frac{r}{2}\right)^3 = \frac{\pi}{6}r^3.\) Thus, \[P(\text{closer to center than outside}) = \dfrac{\text{volume of desired outcomes}}{\text{volume of total outcomes}} = \frac{\frac{\pi}{6}r^3}{\frac{4\pi}{3} r^3} = \frac{1}{8} = 12.5\%.\ _\square\]

Of course, not all problems will be so explicitly geometric in nature. As usual, one of the signs that we might want to apply geometric probability is that we are dealing with continuous variables. Let's see how we can approach the following example:

Alex, Bob, and Charlie each randomly pick a real number between 0 and 1. What is the probability that the sum of the squares of their numbers does not exceed 1? First, if we let their 3 numbers be \(x,\) \(y,\) and \(z,\) it is easy to see that the outcomes can be represented as points within a unit cube \(\big(\)the cube that encloses the region \(x,y,z \in [0,1]\big),\) which has volume \(1^3 = 1.\) Then, the region where the sum of the squares of their numbers does not exceed 1 is given by \(x^2+y^2+z^2 \le 1,\) which (without restriction) is the sphere of radius 1 centered around the origin \((0,0,0).\) However, since \(x,y,z\ge 0,\) exactly \(\left(\frac{1}{2}\right)^3 = \frac{1}{8}\) of this sphere (one "octant") lies within the unit cube of possible outcomes. Hence, the volume of this "success" region is \(\frac{1}{8} \cdot \left(\frac{4\pi}{3} \cdot 1^3\right) = \frac{\pi}{6}.\) Thus, \[P(\text{sum of squares does not exceed 1}) = \dfrac{\text{volume of desired outcomes}}{\text{volume of total outcomes}} = \frac{\frac{\pi}{6}}{1} = \frac{\pi}{6} = 52\%.\ _\square\]

If 3 real numbers are chosen randomly and uniformly from \([0,1],\) what is the probability that the square of one of the numbers will be greater than the sum of the squares of the other two numbers?

In addition to being a useful mathematical problem-solving tool, geometric probability can also be applied in other scientific fields. Let's start with an example from mechanics, using the ideas of velocity and acceleration .

We are playing shuffleboard on the table below, where the lengths of the regions are labelled below (in meters). You push the puck with initial velocity \(v,\) where \(v\) is randomly chosen between 5 and 15 meters/second. Since the table is rough, the puck decelerates at a constant rate of 5 m/s\(^2.\) What is the probability that you slide the puck off of the table? (You may assume that the puck is negligibly small.) In this problem, we have only one variable--the initial speed of the puck--so this is going to be a 1-dimensional geometry problem. Recall the kinematics formula \( v_{f} ^{2} = v_{i}^{2} + 2 a s \). The final speed \(v_ {f }\) is zero because the puck comes to a rest. The initial speed \( v_{i} = v\). The distance traveled \(s\) will decide how many points we get. After plugging in the values, we get \[s = \frac{ v^{ 2 } }{ 10 }, \] so \(s>8+4+2+1=15\) occurs when \(v>\sqrt{150}.\) If we think of \(v\) as being a point on a number line between 5 and 15, then we can find our probability as \[\frac{15-\sqrt{150}}{15-5} \approx 28\%.\ _\square\]

Awesome! Who would have expected that geometric probability would allow us to solve a physics problem? Let's check out a few more examples.

A block performs simple harmonic motion with time period \(T\) and maximum speed \(v\). The speed of the block is measured at a random time. What is the probability that the measured speed is more than \(\frac v2?\) Let's plot the block's position (light gray) and velocity (gray). As we are interested in relative values, the specific vertical scaling of the plot is not important. Green time intervals represent times at which we would do a positive measure, where the measured speed, or absolute value of velocity, would exceed \(\frac v2\). These intervals are \(\left(k \pi + \frac{\pi}6, k \pi + 5 \cdot \frac{\pi}6\right)\) for any whole number \(k\), since the start of the first green interval from the vertical axis is at time \(t\) for which \(-\sin{t} = -\frac12\), so \(t = \frac{\pi}6\). Since the motion is periodic and the measure can take place at any time with equal probability, we can argue that the probability of a positive measure is \[\frac{N \times 2 \left(5\cdot \frac{\pi}6 -\frac{\pi}6\right)}{N \times 2\pi} = \frac{2}{3},\] where the system makes \(N\) periods. \(_\square\)

Johannes Kepler worked out that all planets revolve around the sun in elliptical orbits with the sun at one focus. He also deduced that planets revolve around the sun with constant areal velocity. Let's model a small star system in which a planet revolves around the star in an elliptical orbit. It has semi-major axis \(a\) and semi-minor axis \(b\). During one revolution, the minimum speed of the planet is \(u\) and the maximum speed is \(v\). In a complete revolution, an instant of time is randomly and uniformly chosen. What is the probability that the distance between the planet and the star at that instant is more than \(b?\) Kepler observed that planets don't orbit the sun at a uniform speed, but rather move faster when they are closer to the sun and more slowly when they are farther away. He specifically determined that the orbital speed of a planet is such that the line drawn from the sun to the planet sweeps out equal areas in equal intervals of time. This means that the time the planet spends at distant positions is proportional to the area the line sweeps at those positions. Our probability is then \[ \mathbb{P}\big[(\text{measured distance}) > b\big] = \frac{(\text{time spent at distance}) > b}{(\text{time period})} = \frac{A}{A_0} = \frac{A}{\pi \, a \, b}, \] where \(A_0\) is the area of the ellipse and \(A\) is the unknown area that the sun-planet radius vector sweeps out while the planet is far away. The problem then reduces to finding this area: Let's draw the orbit in Cartesian coordinates with \(x\) and \(y\) in units of semi-axis \(a\). Let axis ratio \(\mu =\frac ba\), with \(\mu = 0.6\) in the picture above. The sun is at the left focus \(S\) with coordinates \(\big(-\sqrt{a^2 - b^2}, 0\big).\) Draw a circle with radius \(b\) that is centered at the sun, and find an intersection with the ellipse at point \(P\) with coordinates \(\left( -a \, \sqrt{\frac{a - b}{a + b}}, \sqrt{\frac{2 \, b^3}{a + b}} \right).\) This follows by writing down the equations of the ellipse and circle, respectively: \[\begin{align} \left(\frac{x}{a}\right)^2 + \left(\frac{y}{b}\right)^2 &= 1 \\ (x + c)^2 + y^2 &= b^2 \end{align} \] with \(c = \sqrt{a^2 - b^2}\), and by finding point \(P\) at which the curves meet. We will naturally divide the calculation of the area by integrating the upper branch of the ellipse from the \(x\)-coordinate of \(P\), and by adding the area of triangle \(P S Q\). The picture indicates area division by different shades of green: \[ \begin{align} A &= 2 \times \Bigg( \frac{1}{2} \cdot \left(c - a \, \sqrt{\frac{a - b}{a + b}}\right) \cdot \sqrt{\frac{2 \, b^3}{a + b}} + b \, \int_{x_1}^{x_2} \sqrt{1 - \left(\frac{x}{a}\right)^2} \, dx \Bigg)\\ &= \frac{1}{2} + \frac{1}{\pi} \cdot \left( \sqrt{2 \, \mu \, (1 - \mu)} + \arcsin{\sqrt{\frac{1 - \mu}{1 + \mu}}} \right). \end{align} \] We integrated from \( x_1 = -a \, \sqrt{\frac{a - b}{a + b}} \) to \( x_2 = a \). Below is the plot of the resulting probability in terms of axis ratio \(\mu\). With \(\mu = 0.6\) the probability of finding the planet farther than \(b\) is about 89%. \(_\square\) With the eccentricity of the orbit close to zero, the ellipse is heavily prolonged and the chance of finding the planet in the vicinity of the sun is small, because i) the major part of the orbit is farther from sun, and ii) when the planet does approach the sun, its speed is large, and hence its visitation time is short. On the other hand, when the eccentricity is close to one, the ellipse is close to a circle and the orbital velocity of the planet is approximately constant, which means that the planet spends about half the time at distances less than \(b\), and half the time farther away. This can be seen in the animation below where the axis ratio \( \mu \) oscillates between \(0.2\) and \(0.99\). Caveat: Imagine the ideal case \( b = a \) of a perfect circle. If a planet orbits its sun at a constant distance \( b,\) we surely could never measure its distance at more than \( b \). But the result above suggests the chance should be even. How would you explain this?

There are many great problems in geometric probability. If you'd like some extra challenges, check out these problems. If you'd like to contribute to this wiki, you can add a solution to one of the examples!

Two numbers are chosen randomly and uniformly from \([-a, a]\). What is the probability that the absolute value of the smaller number is greater than two times the absolute value of the larger number? Does the final answer depend on the value of \(a?\) Let \(X\) and \(Y\) represent the two random numbers. Chances of \(X\) being smaller than \(Y\) are even, so we can focus on the case \(X < Y\). Our probability is then \[ \mathbb{P} \big( |X| > 2 \cdot |Y| \big) = \frac{a^2}{2} : \frac{(2 a)^2}{2} = \frac{1}{4}. \] The probability expression involves two absolute values, so it splits to four cases, depending on the signs of the variates: i) \( (X < 0) \land (Y > 0)\) ii) \( (X < 0) \land (Y < 0)\) iii) \( (X > 0) \land (Y > 0)\) iv) \( (X > 0) \land (Y < 0)\). Solutions of the last two, together with the starting assumption, are empty sets. The union of the solutions of the first two cases is shaded in the picture below. Mind that we divided by half of the area of the square \(2 \cdot a^2\), since we started by reducing the probability space to the region above the line \(X = Y\). Note also that the answer doesn't involve \(a\), so that it would stay the same as long as we picked the two variates from some common interval. \(_\square\)

Two points are randomly and uniformly selected on the circumference of a circle. The center of the circle and the two points are joined together. What is the probability that we obtain each of the following? \(\begin{array}{rrl} &\text{i)} &\text{a line segment} \\ &\text{ii)} &\text{an acute-angled triangle} \\ &\text{iii)} &\text{a right-angled triangle} \\ &\text{iv)} &\text{an obtuse-angled triangle} \end{array}\) We may suppose that the two points \(A\) and \(B\) are selected independently so we can, without loss of generality, select and place \(B\) relatively to \(A\). i) Answer: \(0\). Why? Line segment would occur if \(B\) was placed at exact angle \(\pi\) to \(A\). But a continuous variable has zero chance of taking a specific value (what is the width of a point?). ii) Answer: \(\frac{1}{2}\). Why? Triangle would be acute if \(B\) was placed at some angle in the interval \(\big[-\frac{\pi}{2}, \frac{\pi}{2}\big]\). Values \(-\frac{\pi}{2}\) and \(\frac{\pi}{2}\) (such triangle would be right-angled ) and \(0\) ( degenerate ) should be excluded, yet again, some specific discrete values don't change the probability. iii) Answer: \(0\). Why? See above. iv) Answer: \(\frac{1}{2}\). Why? Triangle can be either acute or obtuse, with even chances. \(_\square\)

Two points are randomly and uniformly selected from the interior of a circle. The center of the circle and the two points are joined together. What is the probability that we obtain each of the following? \(\begin{array}{rrl} &\text{i)} &\text{a line segment} \\ &\text{ii)} &\text{an acute-angled triangle} \\ &\text{iii)} &\text{a right-angled triangle} \\ &\text{iv)} &\text{an obtuse-angled triangle} \end{array}\)

Two points are chosen randomly and uniformly along a stick of length \(1.\) The stick is cut at those points to form \(3\) pieces. What is the probability that these pieces can form a triangle?

Two real numbers \(a\) and \(b\) are randomly chosen from the range \((0,1).\) The probability that \(\frac{a}{b}\) rounded to the nearest integer is odd is equal to \(P.\) What is \(\lfloor1000P\rfloor?\)

Large tablecloth has parallel vertical lines unit apart. Thin wooden stick of length \( \frac{3}{2} \) is twirled and tossed on the table. If \(P\) is the chance that the stick crosses two lines when it lands and comes to rest, how much is \(10^{10} \times P\), rounded to nearest whole number?

How large is the table exactly? Assume infinite expanse, infinitely thin lines, etc. The picture below depicts some sticks that are colored by the number of crossings.

Master concepts like these

Learn more in our Applied Probability course, built by experts for you.

Problem Loading...

Note Loading...

Set Loading...

Geometric Probabilities Distributions Examples

The geometric probability distribution is used in situations where we need to find the probability \( P(X = x) \) that the \(x\)th trial is the first success to occur in a repeated set of trials. The random variable \( X \) associated with a geometric probability distribution is discrete and therefore the geometric distribution is discrete.

Geometric Probability Formula

If the trials are 1) independent 2) each trial have only two possible mutually exclusive outcomes: success or failure 3) the probability of a success at each trial is \( p \) and is constant 4) the probability of a failure at each trial is \( 1 - p \) (probability of complement) and is constant We have a geometric probability distribution and the probability \( P(X = x) \) that the the \( x\)th trial is a success is given by \[ P(X = x) = (1 -p)^{x-1} p \quad \text{, for} \quad x = 1, 2, 3, ...\] Explanation of the formula In order to have a first success at the \( x\)th trial, the first \( x - 1\) trials must be failures each occurring with a probability \( 1 - p\). The probability of having \( x - 1 \) successive failures is given by product rule \[ (1 - p) \times (1-p) \times (1-p) ... = (1-p)^{x-1}\] The \( x\)th trial must be a success occurring with a probability \[ p \] We then use the product rule to write the formula: \( P(X = x) = (1 -p)^{x-1} p \) given above. The mean of the geometric distribution is \( \mu = \dfrac{1}{p} \) The variance of the geometric distribution is \( \sigma^2 = \dfrac{1-p}{p^2} \) The standard deviation of the geometric distribution is \( \sigma = \sqrt{\dfrac{1-p}{p^2}} \)

Geometric Distribution Examples with Detailed Solutions

Example 2 In a large population of adults, 45% have a post secondary degree. If people are selected at random from this population, a) what is the probability that the third person selected is the first one that has a post secondary degree? b) what is the probability that the first person with a post secondary degree is randomly selected on or before the 4th selection? Solution to Example 2 a) Let "having post secondary degree" be a "success". If a person from this population is selected at random, the probability of "having post secondary degree" is \( p = 45\% = 0.45 \) and "not having post secondary degree" (failure) is \( 1 - p = 1 - 0.45 = 0.55 \) Selecting a person from a large population is a trial and these trials may be assumed to be independent. This is a geometric probability problem. Hence \( P(X = 3) = (1-0.45)^2 (0.45) = 0.1361 \). b) On or before the 4th is selected means either the first, second, third or fourth person. The probability may be written as \( P(X \le 4) = P(X = 1) + P(X = 2) + P(X = 3) + P(X = 4) \) Substitute by the formula \( P(X = x) = (1 - 0.45)^{x-1} 0.45 \) to write \( P(X \le 4) = (1 - 0.45)^{1-1} 0.45 + (1 - 0.45)^{2-1} 0.45 + (1 - 0.45)^{3-1} 0.45 + (1 - 0.45)^{4-1} 0.45 = 0.9085 \)

Sums of the terms of a Geometric sequence

As seen above, the geometric probability distribution is given by \[ P(X = x) = (1 -p)^{x-1} p \] Express \( P(X = x) \) for \( x = 1, 2, ...., n .. \) to obtain \( P(X = 1) = p , \quad P(X = 2) = (1 -p) p , \quad P(X = 3) = (1 -p)^{2} p .... \quad P(X = n) = (1 -p)^{n-1} p \) We note that the above are the terms of a geometric sequence hence the name of geometric probability distribution . We need to find a formula for the finite and infinite sums of a the terms of a geometric sequence which will be used to answer the questions in the examples below and write closed form formulas that are easy to use. The finite sum \( S \) of the terms of a geometric sequence with first term \( a _1 \) and \( n\)th term \( a_n = a_1 r^{n-1} \) and common ratio \( r \) is given by \( S = \sum\limits_{x=1}^{n} a_1 r^{x-1} = a_1 + a_1 r + a_1 r^2 + ... a_1 r^{n-1} \) Multiply the left and right hand terms to obtain \( S r = a_1 r + a_1 r^2 + a_1 r^3 + ... a_1 r^n \) Subtract \( S r \) from \( S \) \( S - S r = (a_1 + a_1 r + a_1 r^2 + ... a_1 r^{n-1}) - (a_1 r + a_1 r^2 + a_1 r^3 + ... a_1 r^n) \) Simplify \( S - S r = a_1 - a_1 r^n \) Factor \( S \) out on the left side \( S (1 - r) = a_1 - a_1 r^n \) Solve for the sum \( S \) to find the formula \[ S = \sum\limits_{x=1}^{n} a_1 r^{x-1} = \dfrac{a_1(1 - r^n)}{1-r} \; , \; r \ne 1 \] For \( r \lt 1 \) and the sum is infinite, we have \[ S = \sum\limits_{x=1}^{\infty} a_1 r^{x-1} = \dfrac{a_1}{1-r} \]

Example 3 The trials of a probability experiment satisfy the conditions for a geometric distribution with a probability of success \( p \), find the probability that a) a success occurs on or before the nth trial. b) a success occurs before the nth trial. c) a success occurs on or after the nth trial. d) a success occurs after the nth trial. Solution to Example 3 a) \( P(X \le n) = \sum\limits_{x=1}^{n} P(X = x) = \sum\limits_{x=1}^{n} (1-p)^{x-1} p \) The above is a finite sum of a geometric sequence with the first term \( a_1 = p \) and the nth term \( a_n = (1-p)^{n-1} p \) and the common ratio \( 1 - p \). Hence \( P(X \le n) = \dfrac{p(1 - (1-p)^n)}{1-(1-p)} = 1 - (1-p)^n \) b) \( P(X \lt n) = \sum\limits_{x=1}^{n-1} P(X = x) = \sum\limits_{x=1}^{n-1} (1-p)^{x-1} p \) The above is a finite sum of a geometric sequence with the first term \( a_1 = p \) and the common ratio \( 1 - p \). Hence \( P(X \lt n) = \dfrac{p(1 - (1-p)^{n-1})}{1-(1-p)} = 1 - (1-p)^{n-1} \) c) Using the probability of the complement \( P(X \ge n) = 1 - P(X \lt n) = 1 - (1 - (1-p)^{n-1}) = (1-p)^{n-1} \) d) Using the probability of the complement \( P(X \gt n) = 1 - P(X \le n) = 1 - (1 - (1-p)^n) = (1-p)^n \)

Example 4 A company makes tools such that 99% of these tools are not defective. Tools are selected at random and tested, a) what is the probability that the second selected tool is the first to be non defective? b) what is the probability that the first non defective tool is randomly selected on or before the second selection? c) what is the probability that the first non defective tool is randomly selected after the 10th selection? Solution to Example 4 a) Let "a non defective tool" be a "success" with \( p = 99\% = 0.99 \). \( P(X = 2) = (1-0.99)^{2-1} (0.99) = 0.0099 \). b) On or before the second selection means: \( P(X \le 2)\) Substitute \( n \) by \( 2 \) and \( p \) by \( 0.99 \) in the formula \( P(X \le n) = 1 - (1-p)^n \) obtained in example 3 above. \( P(X \le 2) = 1 - (1-0.99)^2 = 0.9999 \)

More References and links

If you're seeing this message, it means we're having trouble loading external resources on our website.

If you're behind a web filter, please make sure that the domains *.kastatic.org and *.kasandbox.org are unblocked.

To log in and use all the features of Khan Academy, please enable JavaScript in your browser.

AP®︎/College Statistics

Course: ap®︎/college statistics   >   unit 8.

• Geometric random variables introduction
• Binomial vs. geometric random variables
• Geometric distribution mean and standard deviation
• Geometric distributions

Probability for a geometric random variable

• Geometric probability
• Cumulative geometric probability (greater than a value)
• Cumulative geometric probability (less than a value)
• TI-84 geometpdf and geometcdf functions
• Cumulative geometric probability
• Proof of expected value of geometric random variable

Want to join the conversation?

• Upvote Button navigates to signup page
• Downvote Button navigates to signup page
• Flag Button navigates to signup page

Video transcript

• Notes & Study Guides
• Textbook Answers
• Exam Prep Videos
• Login to your account or Register for free
• Notes & Study Guides
• Math / Holt California Geometry 1 / Chapter 9-6

Holt California Geometry 1st Edition solutions

Author: Rinehart, Winston Holt Publisher: HOLT, RINEHART AND WINSTON ISBN: 9780030923456 Buy the book

We have answers for this textbook’s questions Check out the solutions to this books Chapter Problems

Chapter 9 problems, chapter: 9 problem: 1, chapter: 9 problem: 2, chapter: 9 problem: 3, chapter: 9 problem: 4, chapter: 9 problem: 5, chapter: 9 problem: 6, chapter: 9 problem: 7, chapter: 9 problem: 8, chapter: 9 problem: 9, chapter: 9 problem: 10, chapter: 9 problem: 11, chapter: 9 problem: 12, chapter: 9 problem: 13, chapter: 9 problem: 14, chapter: 9 problem: 15, chapter: 9 problem: 16, chapter: 9 problem: 17, chapter: 9 problem: 18, chapter: 9 problem: 19, chapter: 9 problem: 20, chapter: 9 problem: 21, chapter: 9 problem: 22, chapter: 9 problem: 23, chapter: 9 problem: 24, chapter: 9 problem: 25, chapter: 9 problem: 26, chapter: 9 problem: 27, chapter: 9 problem: 28, chapter: 9 problem: 29, chapter: 9 problem: 30, chapter: 9 problem: 31, chapter: 9 problem: 32, chapter: 9 problem: 33, chapter: 9 problem: 34, chapter: 9 problem: 35, chapter: 9 problem: 36, chapter: 9 problem: 37, chapter: 9 problem: 38, chapter: 9 problem: 39, chapter: 9 problem: 40, chapter: 9 problem: 41, chapter: 9 problem: 42, chapter: 9 problem: 43, chapter: 9 problem: 44, chapter: 9 problem: 45, chapter: 9 problem: 46, chapter: 9 problem: 47, chapter: 9 problem: 48, chapter: 9 problem: 49, chapter: 9 problem: 50, chapter: 9 problem: 51, chapter: 9 problem: 52, chapter: 9 problem: 53, chapter: 9 problem: 54, chapter: 9 problem: 55, chapter: 9 problem: 56, chapter: 9 problem: 57, watch the video answers for this chapter.

Login or Sign up for access to all of our study tools and educational content!

Forgot password? Register Now

Sign up for access to all content on our site!

Or login if you already have an account

Reset password

If you have an active account we’ll send you an e-mail for password recovery

Or login if you have your password back

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons

Margin Size

• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

9.3: Geometric Sequences

• Last updated
• Save as PDF
• Page ID 143892

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)

( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

\( \newcommand{\Span}{\mathrm{span}}\)

\( \newcommand{\id}{\mathrm{id}}\)

\( \newcommand{\kernel}{\mathrm{null}\,}\)

\( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\)

\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\)

\( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)

\( \newcommand{\vectorA}[1]{\vec{#1}}      % arrow\)

\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}}      % arrow\)

\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vectorC}[1]{\textbf{#1}} \)

\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)

\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)

\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)

Learning Objectives

• Find the common ratio for a geometric sequence.
• List the terms of a geometric sequence.
• Use a recursive formula for a geometric sequence.
• Use an explicit formula for a geometric sequence.

Many jobs offer an annual cost-of-living increase to keep salaries consistent with inflation. Suppose, for example, a recent college graduate finds a position as a sales manager earning an annual salary of \($26,000\). He is promised a \(2\%\) cost of living increase each year. His annual salary in any given year can be found by multiplying his salary from the previous year by \(102\%\). His salary will be \($26,520\) after one year; \($27,050.40\) after two years; \($27,591.41\) after three years; and so on. When a salary increases by a constant rate each year, the salary grows by a constant factor. In this section, we will review sequences that grow in this way.

Finding Common Ratios

The yearly salary values described form a geometric sequence because they change by a constant factor each year. Each term of a geometric sequence increases or decreases by a constant factor called the common ratio . The sequence below is an example of a geometric sequence because each term increases by a constant factor of 6. Multiplying any term of the sequence by the common ratio 6 generates the subsequent term.

Definition: GEOMETRIC SEQUENCE

A geometric sequence is one in which any term divided by the previous term is a constant. This constant is called the common ratio of the sequence. The common ratio can be found by dividing any term in the sequence by the previous term. If \(a_1\) is the initial term of a geometric sequence and \(r\) is the common ratio, the sequence will be

\[\{a_1, a_1r,a_1r^2,a_1r^3,...\} .\]

How to: Given a set of numbers, determine if they represent a geometric sequence.

• Divide each term by the previous term.
• Compare the quotients. If they are the same, a common ratio exists and the sequence is geometric.

Example \(\PageIndex{1}\): Finding Common Ratios

Is the sequence geometric? If so, find the common ratio.

• \(1\), \(2\), \(4\), \(8\), \(16\),...
• \(48\), \(12\), \(4\), \(2\),...

Divide each term by the previous term to determine whether a common ratio exists.

The sequence is geometric because there is a common ratio. The common ratio is \(2\).

The sequence is not geometric because there is not a common ratio.

The graph of each sequence is shown in Figure \(\PageIndex{1}\). It seems from the graphs that both (a) and (b) appear have the form of the graph of an exponential function in this viewing window. However, we know that (a) is geometric and so this interpretation holds, but (b) is not.

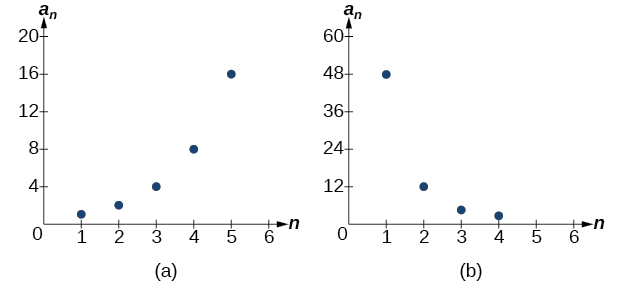
Figure \(\PageIndex{1}\)

If you are told that a sequence is geometric, do you have to divide every term by the previous term to find the common ratio?

No. If you know that the sequence is geometric, you can choose any one term in the sequence and divide it by the previous term to find the common ratio.

Exercise \(\PageIndex{1A}\)

\(5\), \(10\), \(15\), \(20\),...

The sequence is not geometric because \(\dfrac{10}{5}≠\dfrac{15}{10}\)

Exercise \(\PageIndex{1B}\)

\(100\), \(20\), \(4\), \(\dfrac{4}{5}\),...

The sequence is geometric. The common ratio is \(\dfrac{1}{5}\)

Writing Terms of Geometric Sequences

Now that we can identify a geometric sequence, we will learn how to find the terms of a geometric sequence if we are given the first term and the common ratio. The terms of a geometric sequence can be found by beginning with the first term and multiplying by the common ratio repeatedly. For instance, if the first term of a geometric sequence is \(a_1=−2\) and the common ratio is \(r=4\), we can find subsequent terms by multiplying \(−2⋅4\) to get \(−8\) then multiplying the result \(−8⋅4\) to get \(−32\) and so on.

\[\begin{align*} a_1 &= −2 \\ a_2 &= (−2⋅4)=−8 \\ a_3 &= (−8⋅4)=−32 \\ a_4 &= (−32⋅4)=128 \end{align*}\]

The first four terms are \(\{–2, –8, –32, –128\}\).

How to: Given the first term and the common factor, find the first four terms of a geometric sequence.

• Multiply the initial term, \(a_1\), by the common ratio to find the next term, \(a_2\).
• Repeat the process, using \(a_n=a_2\) to find \(a_3\) and then use \(a_3\) to find \(a_4\), until all four terms have been identified.
• Write the terms separated by commons within brackets.

Example \(\PageIndex{2}\): Writing the Terms of a Geometric Sequence

List the first four terms of the geometric sequence with \(a_1=5\) and \(r=–2\).

Multiply \(a_1\) by \(−2\) to find \(a_2\). Repeat the process, using \(a_2\) to find \(a_3\), and so on.

\[\begin{align*} a_1 &= 5 \\ a_2 &= −2a_1=−10 \\ a_3 &= −2a_2=20 \\ a_4 &= −2a_3=−40 \end{align*}\]

The first four terms are \(\{5,–10,20,–40\}\).

Exercise \(\PageIndex{2}\)

List the first five terms of the geometric sequence with \(a_1=18\) and \(r=\dfrac{1}{3}\).

\(\left \{18, 6, 2, \dfrac{2}{3}, \dfrac{2}{9} \right \} \)

Using Recursive Formulas for Geometric Sequences

A recursive formula allows us to find any term of a geometric sequence by using the previous term. Each term is the product of the common ratio and the previous term. For example, suppose the common ratio is \(9\). Then each term is nine times the previous term. As with any recursive formula, the initial term must be given.

Note: RECURSIVE FORMULA FOR A GEOMETRIC SEQUENCE

The recursive formula for a geometric sequence with common ratio r and first term \(a_1\) is

\[a_n=ra_{n−1},\;\;\; n≥2\]

How to: Given the first several terms of a geometric sequence, write its recursive formula.

• State the initial term.
• Find the common ratio by dividing any term by the preceding term.
• Substitute the common ratio into the recursive formula for a geometric sequence.

Example \(\PageIndex{3}\): Using Recursive Formulas for Geometric Sequences

Write a recursive formula for the following geometric sequence.

\(\{6, 9, 13.5, 20.25, ...\} \nonumber\)

The first term is given as \(6\). The common ratio can be found by dividing the second term by the first term.

\(r=\dfrac{9}{6}=1.5 \nonumber\)

Substitute the common ratio into the recursive formula for geometric sequences and define \(a_1\).

\[\begin{align*} a_n &= ra_{n−1} \\ a_n &= 1.5a_{n−1} \text{ for }n≥2 \\ a_1 &= 6 \end{align*}\]

The sequence of data points follows an exponential pattern. The common ratio is also the base of an exponential function as shown in Figure \(\PageIndex{2}\).

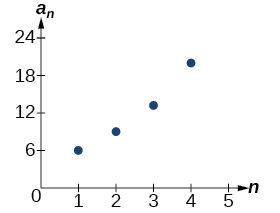
Figure \(\PageIndex{2}\)

Do we have to divide the second term by the first term to find the common ratio?

No. We can divide any term in the sequence by the previous term. It is, however, most common to divide the second term by the first term because it is often the easiest method of finding the common ratio.

Exercise \(\PageIndex{3}\)

\(\{2, \frac{4}{3}, \frac{8}{9}, \frac{16}{27}, ...\}\)

\(\begin{align*}a_1 &= 2 \\ a_n &= \dfrac{2}{3}a_{n−1} \text{ for }n≥2 \end{align*}\)

Using Explicit Formulas for Geometric Sequences

Because a geometric sequence is an exponential function whose domain is the set of positive integers, and the common ratio is the base of the function, we can write explicit formulas that allow us to find particular terms.

\[a_n=a_1r^{n−1}\]

Let’s take a look at the sequence \(\{18, 36, 72, 144, 288, ...\}\). This is a geometric sequence with a common ratio of \(2\) and an exponential function with a base of \(2\). An explicit formula for this sequence is

\(a_n=18·2^{n−1}\)

The graph of the sequence is shown in Figure \(\PageIndex{3}\).

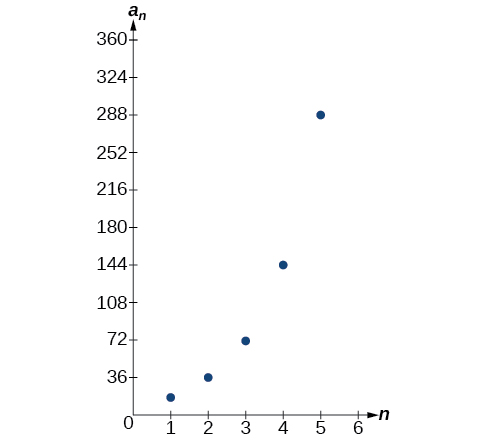
Figure \(\PageIndex{3}\)

Note: EXPLICIT FORMULA FOR A GEOMETRIC SEQUENCE

The \(n^{th}\) term of a geometric sequence is given by the explicit formula :

Example \(\PageIndex{4}\): Writing Terms of Geometric Sequences Using the Explicit Formula

Given a geometric sequence with \(a_1=3\) and \(a_4=24\), find \(a_2\).

The sequence can be written in terms of the initial term and the common ratio \(r\).

\(3\), \(3r\), \(3r^2\), \(3r^3\),...

Find the common ratio using the given fourth term.

\[\begin{align*} a_n&=a_1r^{n-1} \\ a_4&=3r^3 \qquad \text{Write the fourth term of sequence in terms of }\alpha_1 \text{ and } r \\ 24&=3r^3 \qquad \text{Substitute }24 \text{ for }a_4 \\ 8&=r^3 \qquad \text{Divide} \\ r&=2 \qquad \text{Solve for the common ratio} \end{align*}\]

Find the second term by multiplying the first term by the common ratio.

\[\begin{align*} a_2 &= 2 \\ a_1 &= 2(3) \\ & = 6 \end{align*}\]

The common ratio is multiplied by the first term once to find the second term, twice to find the third term, three times to find the fourth term, and so on. The tenth term could be found by multiplying the first term by the common ratio nine times or by multiplying by the common ratio raised to the ninth power.

Exercise \(\PageIndex{4}\)

Given a geometric sequence with \(a_2=4\) and \(2a_3=32\), find \(a_6\).

\(a_6=16,384\)

Example \(\PageIndex{5}\): Writing an Explicit Formula for the n th Term of a Geometric Sequence

Write an explicit formula for the nth term of the following geometric sequence.

\(\{2, 10, 50, 250, ...\}\)

The first term is \(2\). The common ratio can be found by dividing the second term by the first term.

\(\dfrac{10}{2}=5\)

The common ratio is \(5\). Substitute the common ratio and the first term of the sequence into the formula.

\[\begin{align*}a_n &= a_1r^{(n−1)} \\ a_n &= 2⋅5^{n−1} \end{align*}\]

The graph of this sequence in Figure \(\PageIndex{4}\) shows an exponential pattern.

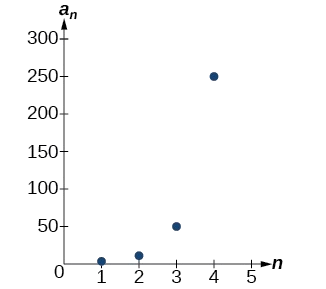
Figure \(\PageIndex{4}\)

Exercise \(\PageIndex{5}\)

Write an explicit formula for the following geometric sequence.

\(\{–1, 3, –9, 27, ...\}\)

\(a_n=−{(−3)}^{n−1}\)

Solving Application Problems with Geometric Sequences

In real-world scenarios involving arithmetic sequences, we may need to use an initial term of \(a_0\) instead of \(a_1\). In these problems, we can alter the explicit formula slightly by using the following formula:

\(a_n=a_0r^n\)

Example \(\PageIndex{6}\): Solving Application Problems with Geometric Sequences

In 2013, the number of students in a small school is \(284\). It is estimated that the student population will increase by \(4\%\) each year.

• Write a formula for the student population.
• Estimate the student population in 2020.

Let \(P\) be the student population and \(n\) be the number of years after 2013. Using the explicit formula for a geometric sequence we get

\(P_n =284⋅{1.04}^n\)

\(2020−2013=7\)

We are looking for the population after \(7\) years. We can substitute \(7\) for \(n\) to estimate the population in 2020.

\(P_7=284⋅{1.04}^7≈374\)

The student population will be about \(374\) in 2020.

Exercise \(\PageIndex{6}\)

A business starts a new website. Initially the number of hits is \(293\) due to the curiosity factor. The business estimates the number of hits will increase by \(2.6%\) per week.

• Write a formula for the number of hits.
• Estimate the number of hits in \(5\) weeks.

\(P_n = 293⋅1.026a^n\)

The number of hits will be about \(333\).

Access these online resources for additional instruction and practice with geometric sequences.

• Geometric Sequences
• Determine the Type of Sequence
• Find the Formula for a Sequence

Key Equations

Key concepts.

• A geometric sequence is a sequence in which the ratio between any two consecutive terms is a constant.
• The constant ratio between two consecutive terms is called the common ratio.
• The common ratio can be found by dividing any term in the sequence by the previous term. See Example \(\PageIndex{1}\).
• The terms of a geometric sequence can be found by beginning with the first term and multiplying by the common ratio repeatedly. See Example \(\PageIndex{2}\) and Example \(\PageIndex{4}\).
• A recursive formula for a geometric sequence with common ratio \(r\) is given by \(a_n=ra_{n–1}\) for \(n≥2\).
• As with any recursive formula, the initial term of the sequence must be given. See Example \(\PageIndex{3}\).
• An explicit formula for a geometric sequence with common ratio \(r\) is given by \(a_n=a_1r^{n–1}\). See Example \(\PageIndex{5}\).
• In application problems, we sometimes alter the explicit formula slightly to \(a_n=a_0r^n\). See Example \(\PageIndex{6}\).

Number Line

• A\:fair\:coin\:is\:tossed\:four\:times\:what\:is\:the\:probability\:of\:obtaining\:at\:least\:three\:heads
• What\:is\:the\:probability\:of\:rolling\:2\:standard\:dice\:which\:sum\:to\:11
• One\:card\:is\:selected\:at\:random\:from\:a\:deck\:of\:cards.\:Determine\:the\:probability\:that\:the\:card\:selected\:is\:a\:9?

probability-problems-calculator

• High School Math Solutions – Inequalities Calculator, Exponential Inequalities Last post, we talked about how to solve logarithmic inequalities. This post, we will learn how to solve exponential...

Please add a message.

Message received. Thanks for the feedback.

Geometry and Probability

Related Topics: More Probability Lessons

In these lessons, we will learn how to solve probability problems that may involve geometry and the area of geometrical shapes.

ABCD is a square. M is the midpoint of BC and N is the midpoint of CD . A point is selected at random in the square. Calculate the probability that it lies in the triangle MCN .

Let 2 x be the length of the square.

Area of square = 2 x × 2 x = 4 x 2

The figure shows a circle with centre O and radius 8 cm. Ð* BOD* = 72˚. The radius of the smaller circle is 4 cm. A point is selected at random inside the larger circle BCDE .

Calculate the probability that the point lies a) inside the sector BODC . b) inside the smaller circle c) neither in the sector BODC nor in the smaller circle.

c) Probability that the point does not lie in sector BODC or the smaller circle

Geometric Probability with Area Example 1: A circle with radius 2 lies inside a square with side length 6. A dart lands randomly inside the square. What is the probability the dart lands inside the circle? Give the exact probability and the probability as a percent rounded to the nearest tenth. Example 2: A point is chosen at random on the given figure. What is the probability that the point is in the yellow region? Example 3: A square is inscribed in a circle. What is the probability that a point chosen inside the circle will be inside the square? Example 4: A circle is inscribed in a equilateral triangle. What is the probability that a point chosen at random inside the triangle will be insode the circle?

Using Area to find Probability Example: A circle is inscribed in a square. Point Q in the square is chosen at random. What is the probability that Q lies in the shaded region?

Geometric Probability and Areas of Sectors Geometric Probability is probability that involves geometric measures (typically length or area) Example: Find the area of the indicated sector. Then find the probability of spinning the color indicated if the diameter is 12 cm.

Study Guide Area Probability Problem 1 Example: Find the probability that a point randomly selected from the figure will land in the shaded area.

Study Guide Area Probability Problem 2 Example: Find the probability that a point randomly selected from the figure will land in the shaded area.

Geometric Probability

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.

PRACTICE PROBLEMS ON PROBABILITY FOR GRADE 9

Problem 1 :

You are walking along a street. If you just choose a stranger crossing you, what is the probability that his next birthday will fall on a Sunday?

Number of days S =  {Monday, Tuesday, Wednesday, Thursday, Friday, Saturday, Sunday}

n(S)  =  7

Let "A" be the event of being birthday on Sunday.

n(A)  =  1

P(A)  =  n(A)/n(S)

P(A)  =  1/7

Problem 2 :

What is the probability of drawing a King or a Queen or a Jack from a deck of cards?

Total number of cards n(S)  =  52

Let "A" be the event of getting king or queen or jack card.

n(A)  =  4 + 4 + 4  =  12

P(A)  =  12/52

p(A)  =  3/13

Problem 3 :

What is the probability of throwing an even number with a single standard dice of six faces?

Sample space  =  {1, 2, 3, 4, 5, 6}

n(S)  =  6

Let "A" be the event of getting even number.

A =  {2, 4, 6}

n(A)  =  3

P(A)  =  n(A)/n(S) 

=  3/6  =  1/2

Problem 4 :

There are 24 balls in a pot. If 3 of them are Red, 5 of them are Blue and the remaining are Green then, what is the probability of picking out (i) a Blue ball, (ii) a Red ball and (iii) a Green ball?

Number of balls n(S)  = 24

Let "A", "B" and "C" be the events of getting red, blue and green balls respectively.

n(A)  =  3, n(B)  =  5, n(C)  =  24 - (5 + 3)  =  16

(i)  p(A)  =  n(A)/n(S)

P(A)  =  3/24

P(A)  =  1/8

(ii)  p(B)  =  n(B)/n(S)

P(B)  =  5/24

(iii)  p(C)  =  n(C)/n(S)

P(C)  =  16/24

P(C)  =  2/3

Problem 5 :

When two coins are tossed, what is the probability that two heads are obtained?

Outcomes of tossing two coins

S  =  { HH, TT, HT, TH}

n(S)  =  4

Let "A" be the event of getting 2 heads.

P(A)  =  n(A)/n(S)  

P(A)  =  1/4

Apart from the stuff given above, if you need any other stuff in math, please use our google custom search here.

Kindly mail your feedback to   [email protected]

We always appreciate your feedback.

© All rights reserved. onlinemath4all.com

• Sat Math Practice
• SAT Math Worksheets
• PEMDAS Rule
• BODMAS rule
• GEMDAS Order of Operations
• Math Calculators
• Transformations of Functions
• Order of rotational symmetry
• Lines of symmetry
• Compound Angles
• Quantitative Aptitude Tricks
• Trigonometric ratio table
• Word Problems
• Times Table Shortcuts
• 10th CBSE solution
• PSAT Math Preparation
• Privacy Policy
• Laws of Exponents

Recent Articles

How to Convert Between Polar and Rectangular Coordinates

May 31, 24 08:11 PM

How to Convert Between Polar and Rectangular Equations

May 31, 24 08:05 PM

SAT Math Videos (Part 2 - No Calculator)

May 25, 24 05:35 AM

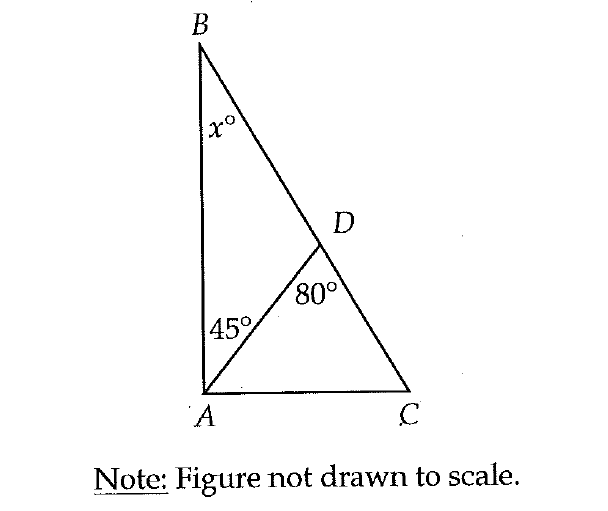
Calculate the price

Minimum Price

PenMyPaper offers you with affordable ‘write me an essay service’

We try our best to keep the prices for my essay writing as low as possible so that it does not end up burning a hole in your pocket. The prices are based on the requirements of the placed order like word count, the number of pages, type of academic content, and many more. At the same time, you can be eligible for some attractive discounts on the overall writing service and get to write with us seamlessly. Be it any kind of academic work and from any domain, our writers will get it done exclusively for you with the greatest efficiency possible.

Is my essay writer skilled enough for my draft?

Customer Reviews

What is the best custom essay writing service?

In the modern world, there is no problem finding a person who will write an essay for a student tired of studying. But you must understand that individuals do not guarantee you the quality of work and good writing. They can steal your money at any time and disappear from sight.

The best service of professional essay writing companies is that the staff give you guarantees that you will receive the text at the specified time at a reasonable cost. You have the right to make the necessary adjustments and monitor the progress of the task at all levels.

Clients are not forced to pay for work immediately; money is transferred to a bank card only after receiving a document.

The services guarantee the uniqueness of scientific work, because the employees have special education and are well versed in the topics of work. They do not need to turn to third-party sites for help. All files are checked for plagiarism so that your professors cannot make claims. Nobody divulges personal information and cooperation between the customer and the contractor remains secret.