High Impact Tutoring Built By Math Experts
Personalized standards-aligned one-on-one math tutoring for schools and districts
Free ready-to-use math resources
Hundreds of free math resources created by experienced math teachers to save time, build engagement and accelerate growth


20 Effective Math Strategies To Approach Problem-Solving
Katie Keeton
Math strategies for problem-solving help students use a range of approaches to solve many different types of problems. It involves identifying the problem and carrying out a plan of action to find the answer to mathematical problems.
Problem-solving skills are essential to math in the general classroom and real-life. They require logical reasoning and critical thinking skills. Students must be equipped with strategies to help them find solutions to problems.
This article explores mathematical problem solving strategies, logical reasoning and critical thinking skills to help learners with solving math word problems independently in real-life situations.
What are problem-solving strategies?
Problem-solving strategies in math are methods students can use to figure out solutions to math problems. Some problem-solving strategies:
- Draw a model
- Use different approaches
- Check the inverse to make sure the answer is correct
Students need to have a toolkit of math problem-solving strategies at their disposal to provide different ways to approach math problems. This makes it easier to find solutions and understand math better.
Strategies can help guide students to the solution when it is difficult ot know when to start.

The ultimate guide to problem solving techniques
Download these ready-to-go problem solving techniques that every student should know. Includes printable tasks for students including challenges, short explanations for teachers with questioning prompts.
20 Math Strategies For Problem-Solving
Different problem-solving math strategies are required for different parts of the problem. It is unlikely that students will use the same strategy to understand and solve the problem.
Here are 20 strategies to help students develop their problem-solving skills.
Strategies to understand the problem
Strategies that help students understand the problem before solving it helps ensure they understand:
- The context
- What the key information is
- How to form a plan to solve it
Following these steps leads students to the correct solution and makes the math word problem easier .
Here are five strategies to help students understand the content of the problem and identify key information.
1. Read the problem aloud
Read a word problem aloud to help understand it. Hearing the words engages auditory processing. This can make it easier to process and comprehend the context of the situation.
2. Highlight keywords
When keywords are highlighted in a word problem, it helps the student focus on the essential information needed to solve it. Some important keywords help determine which operation is needed. For example, if the word problem asks how many are left, the problem likely requires subtraction. Ensure students highlight the keywords carefully and do not highlight every number or keyword. There is likely irrelevant information in the word problem.
3. Summarize the information
Read the problem aloud, highlight the key information and then summarize the information. Students can do this in their heads or write down a quick summary. Summaries should include only the important information and be in simple terms that help contextualize the problem.
4. Determine the unknown
A common problem that students have when solving a word problem is misunderstanding what they are solving. Determine what the unknown information is before finding the answer. Often, a word problem contains a question where you can find the unknown information you need to solve. For example, in the question ‘How many apples are left?’ students need to find the number of apples left over.
5. Make a plan
Once students understand the context of the word problem, have dentified the important information and determined the unknown, they can make a plan to solve it. The plan will depend on the type of problem. Some problems involve more than one step to solve them as some require more than one answer. Encourage students to make a list of each step they need to take to solve the problem before getting started.
Strategies for solving the problem
1. draw a model or diagram.
Students may find it useful to draw a model, picture, diagram, or other visual aid to help with the problem solving process. It can help to visualize the problem to understand the relationships between the numbers in the problem. In turn, this helps students see the solution.

Similarly, you could draw a model to represent the objects in the problem:

2. Act it out
This particular strategy is applicable at any grade level but is especially helpful in math investigation in elementary school . It involves a physical demonstration or students acting out the problem using movements, concrete resources and math manipulatives . When students act out a problem, they can visualize and contectualize the word problem in another way and secure an understanding of the math concepts. The examples below show how 1st-grade students could “act out” an addition and subtraction problem:
| The problem | How to act out the problem |
| Gia has 6 apples. Jordan has 3 apples. How many apples do they have altogether? | Two students use counters to represent the apples. One student has 6 counters and the other student takes 3. Then, they can combine their “apples” and count the total. |
| Michael has 7 pencils. He gives 2 pencils to Sarah. How many pencils does Michael have now? | One student (“Michael”) holds 7 pencils, the other (“Sarah”) holds 2 pencils. The student playing Michael gives 2 pencils to the student playing Sarah. Then the students count how many pencils Michael is left holding. |
3. Work backwards
Working backwards is a popular problem-solving strategy. It involves starting with a possible solution and deciding what steps to take to arrive at that solution. This strategy can be particularly helpful when students solve math word problems involving multiple steps. They can start at the end and think carefully about each step taken as opposed to jumping to the end of the problem and missing steps in between.
For example,

To solve this problem working backwards, start with the final condition, which is Sam’s grandmother’s age (71) and work backwards to find Sam’s age. Subtract 20 from the grandmother’s age, which is 71. Then, divide the result by 3 to get Sam’s age. 71 – 20 = 51 51 ÷ 3 = 17 Sam is 17 years old.
4. Write a number sentence
When faced with a word problem, encourage students to write a number sentence based on the information. This helps translate the information in the word problem into a math equation or expression, which is more easily solved. It is important to fully understand the context of the word problem and what students need to solve before writing an equation to represent it.
5. Use a formula
Specific formulas help solve many math problems. For example, if a problem asks students to find the area of a rug, they would use the area formula (area = length × width) to solve. Make sure students know the important mathematical formulas they will need in tests and real-life. It can help to display these around the classroom or, for those who need more support, on students’ desks.
Strategies for checking the solution
Once the problem is solved using an appropriate strategy, it is equally important to check the solution to ensure it is correct and makes sense.
There are many strategies to check the solution. The strategy for a specific problem is dependent on the problem type and math content involved.
Here are five strategies to help students check their solutions.
1. Use the Inverse Operation
For simpler problems, a quick and easy problem solving strategy is to use the inverse operation. For example, if the operation to solve a word problem is 56 ÷ 8 = 7 students can check the answer is correct by multiplying 8 × 7. As good practice, encourage students to use the inverse operation routinely to check their work.
2. Estimate to check for reasonableness
Once students reach an answer, they can use estimation or rounding to see if the answer is reasonable. Round each number in the equation to a number that’s close and easy to work with, usually a multiple of ten. For example, if the question was 216 ÷ 18 and the quotient was 12, students might round 216 to 200 and round 18 to 20. Then use mental math to solve 200 ÷ 20, which is 10. When the estimate is clear the two numbers are close. This means your answer is reasonable.
3. Plug-In Method
This method is particularly useful for algebraic equations. Specifically when working with variables. To use the plug-in method, students solve the problem as asked and arrive at an answer. They can then plug the answer into the original equation to see if it works. If it does, the answer is correct.

If students use the equation 20m+80=300 to solve this problem and find that m = 11, they can plug that value back into the equation to see if it is correct. 20m + 80 = 300 20 (11) + 80 = 300 220 + 80 = 300 300 = 300 ✓
4. Peer Review
Peer review is a great tool to use at any grade level as it promotes critical thinking and collaboration between students. The reviewers can look at the problem from a different view as they check to see if the problem was solved correctly. Problem solvers receive immediate feedback and the opportunity to discuss their thinking with their peers. This strategy is effective with mixed-ability partners or similar-ability partners. In mixed-ability groups, the partner with stronger skills provides guidance and support to the partner with weaker skills, while reinforcing their own understanding of the content and communication skills. If partners have comparable ability levels and problem-solving skills, they may find that they approach problems differently or have unique insights to offer each other about the problem-solving process.
5. Use a Calculator
A calculator can be introduced at any grade level but may be best for older students who already have a foundational understanding of basic math operations. Provide students with a calculator to allow them to check their solutions independently, accurately, and quickly. Since calculators are so readily available on smartphones and tablets, they allow students to develop practical skills that apply to real-world situations.
Step-by-step problem-solving processes for your classroom
In his book, How to Solve It , published in 1945, mathematician George Polya introduced a 4-step process to solve problems.
Polya’s 4 steps include:
- Understand the problem
- Devise a plan
- Carry out the plan
Today, in the style of George Polya, many problem-solving strategies use various acronyms and steps to help students recall.
Many teachers create posters and anchor charts of their chosen process to display in their classrooms. They can be implemented in any elementary, middle school or high school classroom.
Here are 5 problem-solving strategies to introduce to students and use in the classroom.

How Third Space Learning improves problem-solving
Resources .
Third Space Learning offers a free resource library is filled with hundreds of high-quality resources. A team of experienced math experts carefully created each resource to develop students mental arithmetic, problem solving and critical thinking.
Explore the range of problem solving resources for 2nd to 8th grade students.
One-on-one tutoring
Third Space Learning offers one-on-one math tutoring to help students improve their math skills. Highly qualified tutors deliver high-quality lessons aligned to state standards.
Former teachers and math experts write all of Third Space Learning’s tutoring lessons. Expertly designed lessons follow a “my turn, follow me, your turn” pedagogy to help students move from guided instruction and problem-solving to independent practice.
Throughout each lesson, tutors ask higher-level thinking questions to promote critical thinking and ensure students are developing a deep understanding of the content and problem-solving skills.

Problem-solving
Educators can use many different strategies to teach problem-solving and help students develop and carry out a plan when solving math problems. Incorporate these math strategies into any math program and use them with a variety of math concepts, from whole numbers and fractions to algebra.
Teaching students how to choose and implement problem-solving strategies helps them develop mathematical reasoning skills and critical thinking they can apply to real-life problem-solving.
READ MORE :
- 8 Common Core math examples
- Tier 3 Interventions: A School Leaders Guide
- Tier 2 Interventions: A School Leaders Guide
- Tier 1 Interventions: A School Leaders Guide
There are many different strategies for problem-solving; Here are 5 problem-solving strategies: • draw a model • act it out • work backwards • write a number sentence • use a formula
Here are 10 strategies for problem-solving: • Read the problem aloud • Highlight keywords • Summarize the information • Determine the unknown • Make a plan • Draw a model • Act it out • Work backwards • Write a number sentence • Use a formula
1. Understand the problem 2. Devise a plan 3. Carry out the plan 4. Look back
Some strategies you can use to solve challenging math problems are: breaking the problem into smaller parts, using diagrams or models, applying logical reasoning, and trying different approaches.
Related articles

Why Student Centered Learning Is Important: A Guide For Educators

13 Effective Learning Strategies: A Guide to Using them in your Math Classroom

Differentiated Instruction: 9 Differentiated Curriculum And Instruction Strategies For Teachers

5 Math Mastery Strategies To Incorporate Into Your 4th and 5th Grade Classrooms
Ultimate Guide to Metacognition [FREE]
Looking for a summary on metacognition in relation to math teaching and learning?
Check out this guide featuring practical examples, tips and strategies to successfully embed metacognition across your school to accelerate math growth.
Privacy Overview
Problem Solving: Simplify the Problem

| Add to Folder | |
|---|---|
| creative writing | |
| children's book | |
| activities | |
| classroom tools | |
| language arts and writing | |
| vocabulary |
What Is It?
Simplifying a mathematics problem is a strategy that often is used along with other problem-solving strategies. When a problem is too complex to solve in one step, it often helps to divide it into simpler problems and solve each one separately. Creating a simpler problem from a more complex one may involve rewording the problem; using smaller, simpler numbers; or using a more familiar scenario to understand the problem and find the solution. For example, consider the problem:
A soccer team won 24 of 36 games in the first season. If the team had the same ratio of wins to games in the second season, and they won 16 games, how many games did they play in the second season?
The answer can be found by simplifying the ratio of 24:36 to 2:3, and then cross-multiplying to find the total number of games in the second season, 24 games.
Why Is It Important?
This is a problem-solving strategy that can be used with difficult concepts such as manipulating ratios or fractions. If a problem is confusing, the numbers can be rounded, or simpler numbers can be used to help make a plan to solve it.
How Can You Make It Happen?
Introduce a problem to students that is complex and might be easier to solve if it were simplified. For example:
On your way to visit a friend, you leave your house at 2:45 P.M. and travel 1 3/4 miles to the train, 12 1/2 miles on the train, and 3/4 mile to your friend's house from the train station. If you get there at 4:15 P.M., how many miles per hour did you travel?
Understand the Problem
Demonstrate that the first step is understanding the problem. This involves identifying the key pieces of information needed to find the answer. Students may need to read the problem several times and/or put the problem into their own words.
I know I left at a certain time, arrived at a certain time, and traveled a certain distance. I need to find how many miles per hour I traveled.
Choose a Strategy
For this problem, it might be helpful for students to use simpler numbers to learn the steps they need to follow to solve it. Have students change the problem to:
I left the house 1:00, traveled 12 miles, and arrived at 4:00. How many miles per hour did I travel?
Solve the Problem
First, have students solve the problem using the simpler numbers.
I left the house 1:00, traveled 12 miles, and arrived at 4:00. How many miles per hour did I travel? I traveled 12 miles. It took 3 hours. To find the miles per hour, I divide 12 by 3 to get 4 miles per hour.
Next, have them write down the steps they used to solve the problem.
Find the distance traveled.
Find the time spent.
Divide to find the miles per hour.
Then, have them use the actual numbers from the problem and follow the same steps.
Find the distance traveled. 1 3/4 + 12 1/2 + 3/4 = 15 miles
Find the time spent. The time from 2:45 to 4:15 is 1 hour and 30 minutes, or 1 1/2 hours.
Divide to find the miles per hour. 15 divided by 1 1/2 = 10 miles per hour
In This Article:
Featured high school resources.

Related Resources

About the author

TeacherVision Editorial Staff
The TeacherVision editorial team is comprised of teachers, experts, and content professionals dedicated to bringing you the most accurate and relevant information in the teaching space.


Think back to the first problem in this chapter, the ABC Problem . What did you do to solve it? Even if you did not figure it out completely by yourself, you probably worked towards a solution and figured out some things that did not work.
Unlike exercises, there is never a simple recipe for solving a problem. You can get better and better at solving problems, both by building up your background knowledge and by simply practicing. As you solve more problems (and learn how other people solved them), you learn strategies and techniques that can be useful. But no single strategy works every time.
Pólya’s How to Solve It
George Pólya was a great champion in the field of teaching effective problem solving skills. He was born in Hungary in 1887, received his Ph.D. at the University of Budapest, and was a professor at Stanford University (among other universities). He wrote many mathematical papers along with three books, most famously, “How to Solve it.” Pólya died at the age 98 in 1985. [1]
In 1945, Pólya published the short book How to Solve It , which gave a four-step method for solving mathematical problems:
- Understand the problem.
- Devise a plan.
- Carry out the plan.
- Looking back.
This is all well and good, but how do you actually do these steps?!?! Steps 1. and 2. are particularly mysterious! How do you “make a plan?” That is where you need some tools in your toolbox, and some experience to draw upon.
Much has been written since 1945 to explain these steps in more detail, but the truth is that they are more art than science. This is where math becomes a creative endeavor (and where it becomes so much fun). We will articulate some useful problem solving strategies, but no such list will ever be complete. This is really just a start to help you on your way. The best way to become a skilled problem solver is to learn the background material well, and then to solve a lot of problems!
We have already seen one problem solving strategy, which we call “Wishful Thinking.” Do not be afraid to change the problem! Ask yourself “what if” questions:
- What if the picture was different?
- What if the numbers were simpler?
- What if I just made up some numbers?
You need to be sure to go back to the original problem at the end, but wishful thinking can be a powerful strategy for getting started.
This brings us to the most important problem solving strategy of all:
Problem Solving Strategy 2 (Try Something!). If you are really trying to solve a problem, the whole point is that you do not know what to do right out of the starting gate. You need to just try something! Put pencil to paper (or stylus to screen or chalk to board or whatever!) and try something. This is often an important step in understanding the problem; just mess around with it a bit to understand the situation and figure out what is going on.
And equally important: If what you tried first does not work, try something else! Play around with the problem until you have a feel for what is going on.
Problem 2 (Payback)
Last week, Alex borrowed money from several of his friends. He finally got paid at work, so he brought cash to school to pay back his debts. First he saw Brianna, and he gave her 1/4 of the money he had brought to school. Then Alex saw Chris and gave him 1/3 of what he had left after paying Brianna. Finally, Alex saw David and gave him 1/2 of what he had remaining. Who got the most money from Alex?
Think/Pair/Share
After you have worked on the problem on your own for a while, talk through your ideas with a partner (even if you have not solved it). What did you try? What did you figure out about the problem?
This problem lends itself to two particular strategies. Did you try either of these as you worked on the problem? If not, read about the strategy and then try it out before watching the solution.
Problem Solving Strategy 3 (Draw a Picture). Some problems are obviously about a geometric situation, and it is clear you want to draw a picture and mark down all of the given information before you try to solve it. But even for a problem that is not geometric, like this one, thinking visually can help! Can you represent something in the situation by a picture?
Draw a square to represent all of Alex’s money. Then shade 1/4 of the square — that’s what he gave away to Brianna. How can the picture help you finish the problem?
After you have worked on the problem yourself using this strategy (or if you are completely stuck), you can watch someone else’s solution.
Problem Solving Strategy 4 (Make Up Numbers). Part of what makes this problem difficult is that it is about money, but there are no numbers given. That means the numbers must not be important. So just make them up!
You can work forwards: Assume Alex had some specific amount of money when he showed up at school, say $100. Then figure out how much he gives to each person. Or you can work backwards: suppose he has some specific amount left at the end, like $10. Since he gave Chris half of what he had left, that means he had $20 before running into Chris. Now, work backwards and figure out how much each person got.
Watch the solution only after you tried this strategy for yourself.
If you use the “Make Up Numbers” strategy, it is really important to remember what the original problem was asking! You do not want to answer something like “Everyone got $10.” That is not true in the original problem; that is an artifact of the numbers you made up. So after you work everything out, be sure to re-read the problem and answer what was asked!
Problem 3 (Squares on a Chess Board)
How many squares, of any possible size, are on a 8 × 8 chess board? (The answer is not 64… It’s a lot bigger!)
Remember Pólya’s first step is to understand the problem. If you are not sure what is being asked, or why the answer is not just 64, be sure to ask someone!
Think / Pair / Share
After you have worked on the problem on your own for a while, talk through your ideas with a partner (even if you have not solved it). What did you try? What did you figure out about the problem, even if you have not solved it completely?
It is clear that you want to draw a picture for this problem, but even with the picture it can be hard to know if you have found the correct answer. The numbers get big, and it can be hard to keep track of your work. Your goal at the end is to be absolutely positive that you found the right answer. You should never ask the teacher, “Is this right?” Instead, you should declare, “Here’s my answer, and here is why I know it is correct!”
Problem Solving Strategy 5 (Try a Simpler Problem). Pólya suggested this strategy: “If you can’t solve a problem, then there is an easier problem you can solve: find it.” He also said: “If you cannot solve the proposed problem, try to solve first some related problem. Could you imagine a more accessible related problem?” In this case, an 8 × 8 chess board is pretty big. Can you solve the problem for smaller boards? Like 1 × 1? 2 × 2? 3 × 3?
Of course the ultimate goal is to solve the original problem. But working with smaller boards might give you some insight and help you devise your plan (that is Pólya’s step (2)).
Problem Solving Strategy 6 (Work Systematically). If you are working on simpler problems, it is useful to keep track of what you have figured out and what changes as the problem gets more complicated.
For example, in this problem you might keep track of how many 1 × 1 squares are on each board, how many 2 × 2 squares on are each board, how many 3 × 3 squares are on each board, and so on. You could keep track of the information in a table:
| 1 | 0 | 0 | 0 | ||
| 4 | 1 | 0 | 0 | ||
| 9 | 4 | 1 | 0 | ||
Problem Solving Strategy 7 (Use Manipulatives to Help You Investigate). Sometimes even drawing a picture may not be enough to help you investigate a problem. Having actual materials that you move around can sometimes help a lot!
For example, in this problem it can be difficult to keep track of which squares you have already counted. You might want to cut out 1 × 1 squares, 2 × 2 squares, 3 × 3 squares, and so on. You can actually move the smaller squares across the chess board in a systematic way, making sure that you count everything once and do not count anything twice.
Problem Solving Strategy 8 (Look for and Explain Patterns). Sometimes the numbers in a problem are so big, there is no way you will actually count everything up by hand. For example, if the problem in this section were about a 100 × 100 chess board, you would not want to go through counting all the squares by hand! It would be much more appealing to find a pattern in the smaller boards and then extend that pattern to solve the problem for a 100 × 100 chess board just with a calculation.
If you have not done so already, extend the table above all the way to an 8 × 8 chess board, filling in all the rows and columns. Use your table to find the total number of squares in an 8 × 8 chess board. Then:
- Describe all of the patterns you see in the table.
- Can you explain and justify any of the patterns you see? How can you be sure they will continue?
- What calculation would you do to find the total number of squares on a 100 × 100 chess board?
(We will come back to this question soon. So if you are not sure right now how to explain and justify the patterns you found, that is OK.)
Problem 4 (Broken Clock)
This clock has been broken into three pieces. If you add the numbers in each piece, the sums are consecutive numbers. ( Consecutive numbers are whole numbers that appear one after the other, such as 1, 2, 3, 4 or 13, 14, 15.)
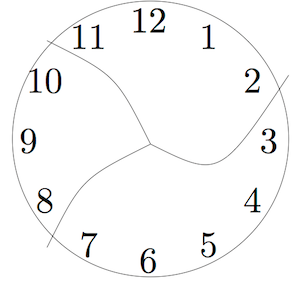
Can you break another clock into a different number of pieces so that the sums are consecutive numbers? Assume that each piece has at least two numbers and that no number is damaged (e.g. 12 isn’t split into two digits 1 and 2.)
Remember that your first step is to understand the problem. Work out what is going on here. What are the sums of the numbers on each piece? Are they consecutive?
After you have worked on the problem on your own for a while, talk through your ideas with a partner (even if you have not solved it). What did you try? What progress have you made?
Problem Solving Strategy 9 (Find the Math, Remove the Context). Sometimes the problem has a lot of details in it that are unimportant, or at least unimportant for getting started. The goal is to find the underlying math problem, then come back to the original question and see if you can solve it using the math.
In this case, worrying about the clock and exactly how the pieces break is less important than worrying about finding consecutive numbers that sum to the correct total. Ask yourself:
- What is the sum of all the numbers on the clock’s face?
- Can I find two consecutive numbers that give the correct sum? Or four consecutive numbers? Or some other amount?
- How do I know when I am done? When should I stop looking?
Of course, solving the question about consecutive numbers is not the same as solving the original problem. You have to go back and see if the clock can actually break apart so that each piece gives you one of those consecutive numbers. Maybe you can solve the math problem, but it does not translate into solving the clock problem.
Problem Solving Strategy 10 (Check Your Assumptions). When solving problems, it is easy to limit your thinking by adding extra assumptions that are not in the problem. Be sure you ask yourself: Am I constraining my thinking too much?
In the clock problem, because the first solution has the clock broken radially (all three pieces meet at the center, so it looks like slicing a pie), many people assume that is how the clock must break. But the problem does not require the clock to break radially. It might break into pieces like this:
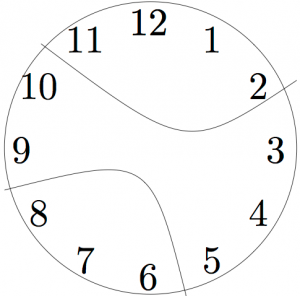
Were you assuming the clock would break in a specific way? Try to solve the problem now, if you have not already.
- Image of Pólya by Thane Plambeck from Palo Alto, California (Flickr) [CC BY 2.0 (http://creativecommons.org/licenses/by/2.0)], via Wikimedia Commons ↵
Mathematics for Elementary Teachers Copyright © 2018 by Michelle Manes is licensed under a Creative Commons Attribution-ShareAlike 4.0 International License , except where otherwise noted.
Share This Book
My Learning Springboard
School Planning | Academic Tutoring | Test Preparation
A Multidisciplinary Educational Consulting Firm
More results...
Problem-Solving Strategies
January 26, 2021 Brad Hoffman Leave a Comment

Certainly, many students find that it is possible to solve a given word problem with minimal consideration of how to approach it. People have varying degrees of “math sense.” Some find most math problems mysterious. Some, however, can very easily see what to do to find solutions; it almost seems obvious to them. But even for students with strong “math sense,” there come those situations when they don’t intuitively know what to do. For all learners, the recognition of specific problem-solving strategies to solve math problems is useful. Thinking about our own thinking (aka metacognition) is important in developing flexibility so that we can see more than one way to solve a particular problem. Math journaling supports this thinking and development.
Below you will find a list of some very useful problem-solving strategies . One thing that is particularly beneficial about this set of strategies is that they are, in fact, universal. In other words, they will work regardless of the math program a student might be using. Whether it’s Singapore Math or Everyday Math or something else entirely , these problem-solving strategies can provide a clear path toward solutions. Interestingly, they can even extend to problem-solving outside the area of math! Becoming familiar with them and comfortable using them can be a big help to students as they wend their way through problems, be they less or more complex.
10 Problem-Solving Strategies
- Make a model/Act out
- Draw a diagram or picture
- Look for a pattern
- Make an organized list
- Make a table
- Guess & Check
- Make it simpler
- Work backwards
- Use logical reasoning
Here are some examples of problems and how to use these strategies.
“How many complete turns does the hour hand on a clock make in one day?”
From the list of problem-solving strategies above, “make a model or act it out” is an excellent choice for this problem. A student could use a model or a real analog clock and turn the hands and count. Distinguishing between the minute and the hour hand and recognizing that the clock only shows 12 of the 24 hours in a day lets the student see that the hour hand makes two complete turns. A physical clock that a student can actually turn provides an important concrete experience that may prove helpful for finding the solution.
“Using each of the digits 0, 1, 2, 3, 4 only once, make a two-digit number times a three-digit number multiplication problem with the greatest product.”
Students can “ draw a diagram or picture” of an “empty” multiplication problem with a box for each digit. Consider which two digits give the largest product and put them in the highest place value spots. Then, if it’s not immediately evident to the student, use one of the other problem-solving strategies — “ guess and check” — to place the remaining digits in the remaining spots. Check by multiplying the results to identify which is actually the largest (e.g. Is it 430 x 21 or 320 x 41?)
“How many even numbers are there between 201 and 351?”
In this instance, “ look for a pattern” would be especially helpful from the list of problem-solving strategies. Either write all numbers from 201 through 351 and notice the pattern that there are 5 in every set of 10 numbers (e.g. 201-210), and then count how many sets of 10 numbers there are and multiply that by 5, or simply write one set of 10 numbers and identify the 5 in 10 pattern without writing out all of them. Either way is valid.
“You have two noses and three hats. How many different nose-hat disguises can you wear?”
For this problem, “ make an organized list ” from the problem-solving strategies listed above works well. The list will start with Hat A and match with each nose (2), then Hat B with each nose (2), then Hat C with each nose (2). This gives a total of 6 disguises.
“How many numbers between 10 and 30 give a remainder of 2 when divided by 3?” You could “ make a table” to find the solution.
| Number | Divided by 3 | Remainder | 2? |
| 11 | 3 | 2 | yes |
| 12 | 4 | 0 | no |
| 13 | 4 | 1 | no |
| 14 | 4 | 2 | yes |
| etc. |
As the Table continues, a pattern becomes evident (“ look for a pattern ” — overlapping strategy!) in which every third number gives a remainder of 2. Count them for a solution.
“If 25 Glinks equal a Glonk, and 15 Glonks equal a Glooie, how many Glinks equal 2 Glooies?”
Please, “ make it simpler”! That strategy is an especially good choice from the list of problem solving-strategies. Let’s look at a simpler, but similar, problem. It’s simpler because the numbers are smaller, and you could even draw a picture to prove it’s correct.
If 3 Glinks equal a Glonk. And 2 Glonks equal a Glooie. How many Glinks equal a Glooie? Multiply 3×2, which equals 6.
So, if 6 Glinks equal a Glooie, then how many Glinks equal 2 Glooies? Multiply 6×2, which equals 12. So, 12 Glinks equal 2 Glooies.
Now with the larger numbers:
If 25 Glinks equal a Glonk. And 15 Glonks equal a Glooie. How many Glinks equal a Glooie? Multiply 15×25, which equals 750. So, 750 Glinks equal a Glooie.
Then, how many Glinks equal 2 Glooies? Multiply 750×2, which equals 1500. So, there are 1500 Glinks in 2 Glooies.
It’s the same process, with bigger numbers! Much simpler!
“If I add 10 to my age and double it, I am 90. How old am I?”
From the list of problem-solving strategies, this problem begs for the student to “ work backwards”. Simply un-double the 90 and subtract ten. 90 divided by 2 = 45 and 45-10=35. Voilà! The answer is 35 years old! Then reverse again to confirm that the answer is correct.
“Arrange these digits and symbols to make a true number sentence (equation.) 3,1,4,9,+,/,= (Note: the forward slash [/] signifies “divided by”.)
“ Use logical reasoning ” to realize that any order is possible, but a larger number needs to be divided by a smaller number with no remainder (9/3=3) Then 3+1=4, so the sentence 9/3+1=4 is the solution.
For the problems that seem absolutely impossible to solve, your best option is to “ brainstorm” , and that’s on the above list of problem-solving strategies! Try various ideas; work with a partner; explore to see what might work; try everything you can think of! It’s amazing how good ideas will sometimes just pop into one’s head!
As a student works with these problem-solving strategies, it becomes clear that they often overlap (as in the “ draw a picture” / “guess and check” example above, problem #2). Or a student becomes especially attached to a few particular strategies that often work well. Some problems seem to be especially suitable for a particular strategy, while others can be approached from several directions. Having the flexibility to move from one strategy to another helps avoid the serious “I’m STUCK!” situation. Also, using more than one strategy on the same problem allows students to check solutions more efficiently before moving on. Again, however, THINKING about how we are THINKING is very beneficial in developing skills in this area. We call this metacognition .
Solving word problems can be fun, like being a detective who has unusual insight. There are solutions! Enjoy finding them! And make effective use of problem-solving strategies!
By Jean Snyder and Brad Hoffman , Elementary Math Specialists

Leave a Reply Cancel reply
Your email address will not be published. Required fields are marked *
Notify me of follow-up comments by email.
Notify me of new posts by email.
Company Overview
School Planning
Private Tutoring
Test Preparation
- PRINT TO PLAY
- DIGITAL GAMES

Problem-Solving Strategies
October 16, 2019
There are many different ways to solve a math problem, and equipping students with problem-solving strategies is just as important as teaching computation and algorithms. Problem-solving strategies help students visualize the problem or present the given information in a way that can lead them to the solution. Solving word problems using strategies works great as a number talks activity and helps to revise many skills.
Problem-solving strategies
1. create a diagram/picture, 2. guess and check., 3. make a table or a list., 4. logical reasoning., 5. find a pattern, 6. work backward, 1. create a diagram/draw a picture.
Creating a diagram helps students visualize the problem and reach the solution. A diagram can be a picture with labels, or a representation of the problem with objects that can be manipulated. Role-playing and acting out the problem like a story can help get to the solution.
Alice spent 3/4 of her babysitting money on comic books. She is left with $6. How much money did she make from babysitting?
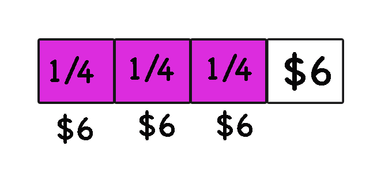
2. Guess and check
Teach students the same strategy research mathematicians use.
With this strategy, students solve problems by making a reasonable guess depending on the information given. Then they check to see if the answer is correct and they improve it accordingly. By repeating this process, a student can arrive at a correct answer that has been checked. It is recommended that the students keep a record of their guesses by making a chart, a table or a list. This is a flexible strategy that works for many types of problems. When students are stuck, guessing and checking helps them start and explore the problem. However, there is a trap. Exactly because it is such a simple strategy to use, some students find it difficult to consider other strategies. As problems get more complicated, other strategies become more important and more effective.
Find two numbers that have sum 11 and product 24.
Try/guess 5 and 6 the product is 30 too high
adjust to 4 and 7 with product 28 still high
adjust again 3 and 8 product 24
3. Make a table or a list
Carefully organize the information on a table or list according to the problem information. It might be a table of numbers, a table with ticks and crosses to solve a logic problem or a list of possible answers. Seeing the given information sorted out on a table or a list will help find patterns and lead to the correct solution.
To make sure you are listing all the information correctly read the problem carefully.
Find the common factors of 24, 30 and 18

Logical reasoning is the process of using logical, systemic steps to arrive at a conclusion based on given facts and mathematic principles. Read and understand the problem. Then find the information that helps you start solving the problem. Continue with each piece of information and write possible answers.
Thomas, Helen, Bill, and Mary have cats that are black, brown, white, or gray. The cats’ names are Buddy, Lucky, Fifi, and Moo. Buddy is brown. Thoma’s cat, Lucky, is not gray. Helen’s cat is white but is not named Moo. The gray cat belongs to Bill. Which cat belongs to each student, and what is its color?
A table or list is useful in solving logic problems.
| Thomas | Lucky | Not gray, the cat is black |
| Helen | Not Moo, not Buddy, not Lucky so Fifi | White |
| Bill | Moo | Gray |
| Mary | Buddy | Brown |
Since Lucky is not gray it can be black or brown. However, Buddy is brown so Lucky has to be black.
Buddy is brown so it cannot be Helen’s cat. Helen’s cat cannot be Moo, Buddy or Lucky, so it is Fifi.
Therefore, Moo is Bill’s cat and Buddy is Mary’s cat.
5. Find a pattern.
Finding a pattern is a strategy in which students look for patterns in the given information in order to solve the problem. When the problem consists of data like numbers or events that are repeated then it can be solved using the “find a pattern” problem-solving strategy. Data can be organized in a table or a list to reveal the pattern and help discover the “rule” of the pattern.
The “rule” can then be used to find the answer to the question and complete the table/list.
Shannon’s Pizzeria made 5 pizzas on Sunday, 10 pizzas on Monday, 20 pizzas on Tuesday, and 40 pizzas on Wednesday. If this pattern continues, how many pizzas will the pizzeria make on Saturday?
| Sunday | 5 |
| Monday | 10 |
| Tuesday | 20 |
| Wednesday | 40 |
| Thursday | |
| Friday | |
| Saturday |
6. Working backward
Problems that can be solved with this strategy are the ones that list a series of events or a sequence of steps .
In this strategy, the students must start with the solution and work back to the beginning. Each operation must be reversed to get back to the beginning. So if working forwards requires addition, when students work backward they will need to subtract. And if they multiply working forwards, they must divide when working backward.
Mom bought a box of candy. Mary took 5 of them, Nick took 4 of them and 31 were given out on Halloween night. The next morning they found 8 pieces of candy in the box. How many candy pieces were in the box when mom bought it.
For this problem, we know that the final number of candy was 8, so if we work backward to “put back” the candy that was taken from the box we can reach the number of candy pieces that were in the box, to begin with.
The candy was taken away so we will normally subtract them. However, to get back to the original number of candy we need to work backward and do the opposite, which is to add them.
8 candy pieces were left + the 31 given out + plus the ones Mary took + the ones Nick took
8+31+5+4= 48 Answer: The box came with 48 pieces of candy.
Selecting the best strategy for a problem comes with practice and often problems will require the use of more than one strategies.
Print and digital activities
I have created a collection of print and digital activity cards and worksheets with word problems (print and google slides) to solve using the strategies above. The collection includes 70 problems (5 challenge ones) and their solution s and explanations.
sample below

How to use the activity cards
Allow the students to use manipulatives to solve the problems. (counters, shapes, lego blocks, Cuisenaire blocks, base 10 blocks, clocks) They can use manipulatives to create a picture and visualize the problem. They can use counters for the guess and check strategy. Discuss which strategy/strategies are better for solving each problem. Discuss the different ways. Use the activities as warm-ups, number talks, initiate discussions, group work, challenge, escape rooms, and more.
Ask your students to write their own problems using the problems in this resource, and more, as examples. Start with a simple type. Students learn a lot when trying to compose a problem. They can share the problem with their partner or the whole class. Make a collection of problems to share with another class.
For the google slides the students can use text boxes to explain their thinking with words, add shapes and lines to create diagrams, and add (insert) tables and diagrams.
Many of the problems can be solved faster by using algebraic expressions. However, since I created this resource for grades 4 and up I chose to show simple conceptual ways of solving the problems using the strategies above. You can suggest different ways of solving the problems based on the grade level.
Find the free and premium versions of the resource below. The premium version includes 70 problems (challenge problems included) and their solutions
There are 2 versions of the resource
70 google slides with explanations + 70 printable task cards
70 google slides with explanations + 11 worksheets
You might also like
Multiplying fractions/mixed numbers/simplifying
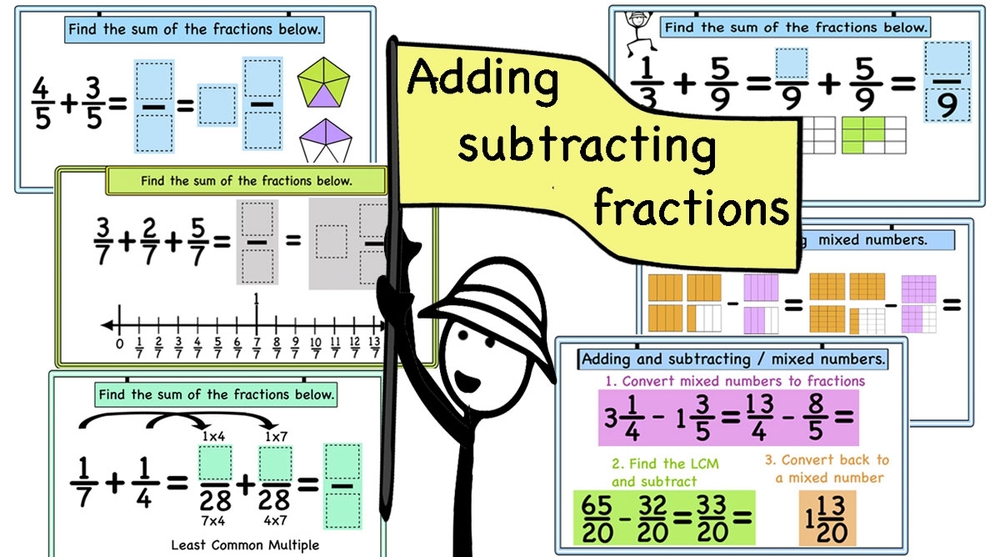
Adding and subtracting fractions
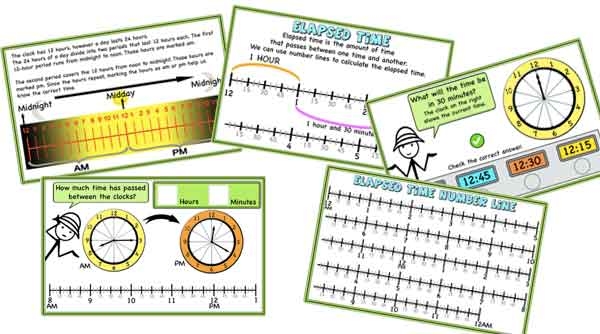
AM/PM, 24-hour clock, Elapsed Time – ideas, games, and activities
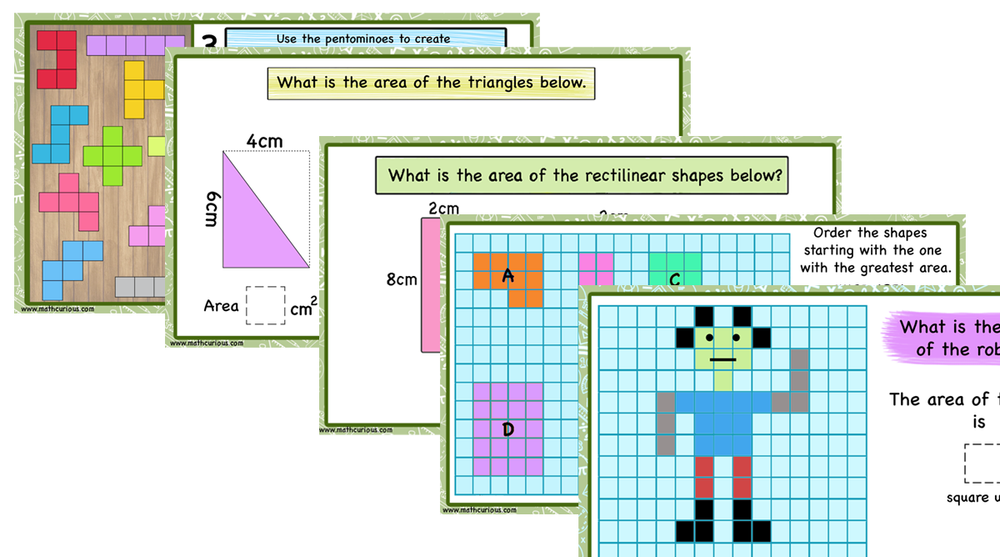
Teaching area, ideas, games, print, and digital activities
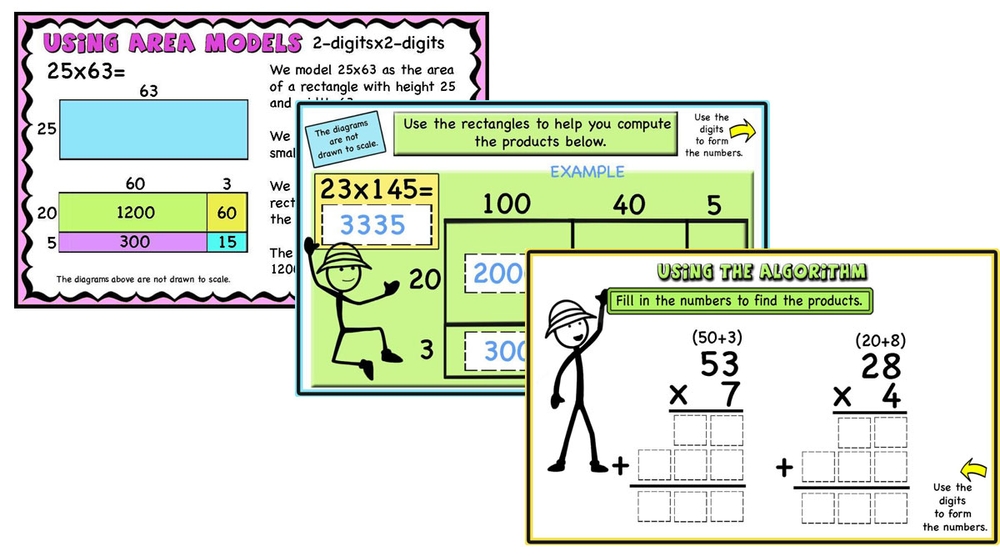
Multi-Digit Multiplication, Area model, Partial Products algorithm, Puzzles, Word problems
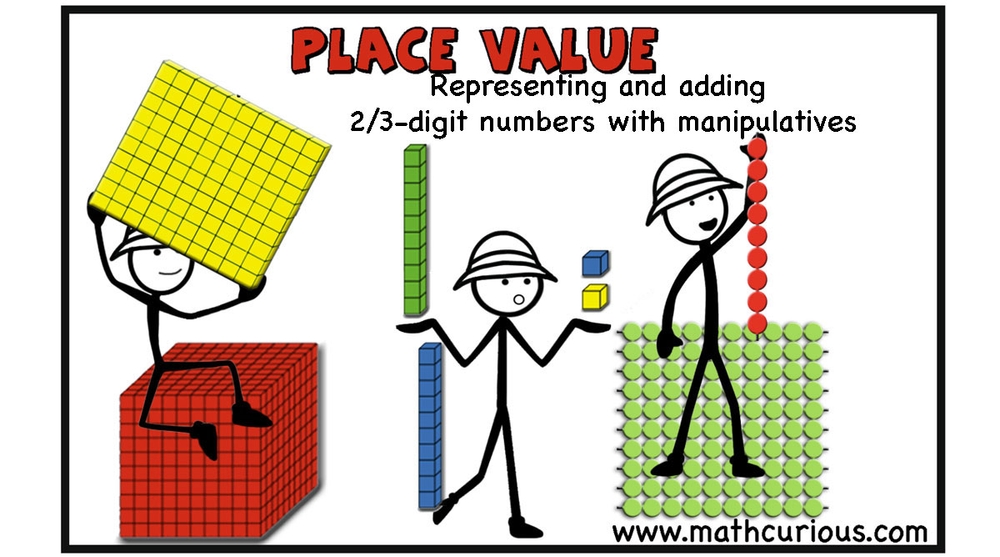
Place Value – Representing and adding 2/3 digit numbers with manipulatives

Multiplication Mission – arrays, properties, multiples, factors, division
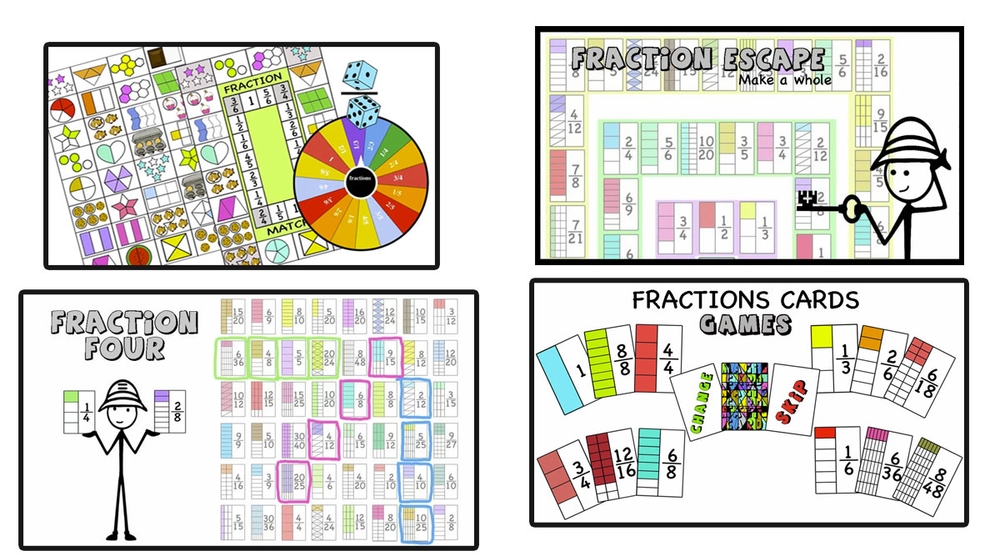
Fractions Games and activities – Equivalence, make 1, compare, add, subtract, like, unlike
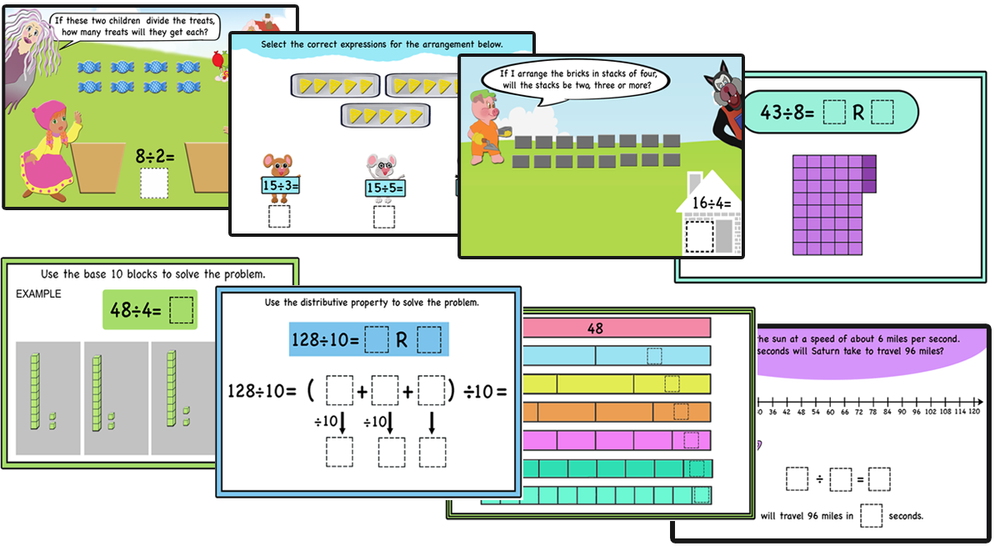
Diving into Division -Teaching division conceptually

Expressions with arrays
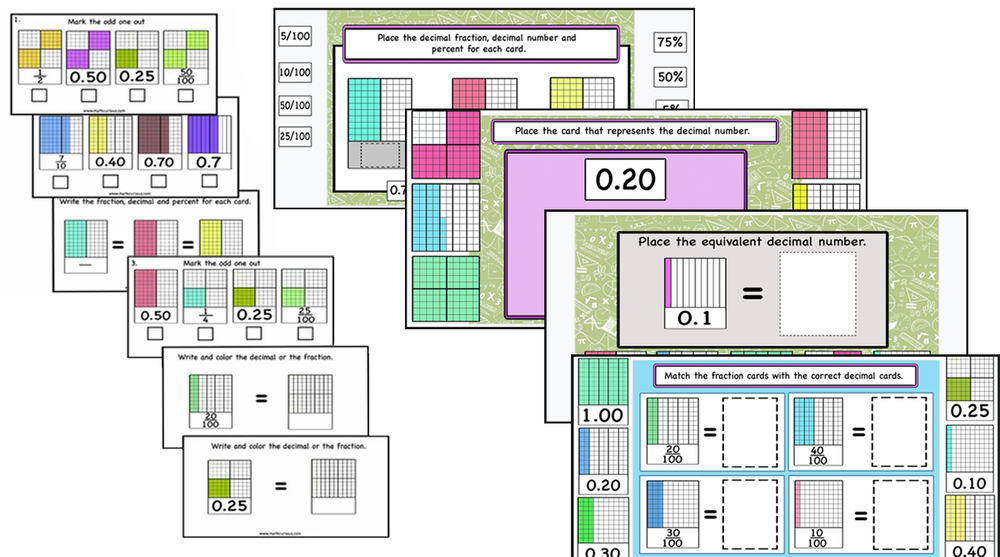
Decimals, Decimal fractions, Percentages – print and digital
Solving Word Problems- Math talks-Strategies, Ideas and Activities-print and digital
Check out our best selling card games now available at amazon.com and amazon.ca.

Chicken Escape
A multiplayer card game that makes mental math practice fun! Chicken Escape is a fast-paced multiplayer card game. While playing…

Dragon Times – A math Adventure card game
Dragon Times is an educational fantasy card game that aims to motivate children to practice multiplication and division facts while…
Appendix A: Applications
Using a problem-solving strategy to solve number problems, learning outcomes.
- Apply the general problem-solving strategy to number problems
- Identify how many numbers you are solving for given a number problem
- Solve consecutive integer problems
Now we will translate and solve number problems. In number problems, you are given some clues about one or more numbers, and you use these clues to build an equation. Number problems don’t usually arise on an everyday basis, but they provide a good introduction to practicing the Problem-Solving Strategy. Remember to look for clue words such as difference , of , and and .
The difference of a number and six is [latex]13[/latex]. Find the number.
| Step 1. the problem. Do you understand all the words? | |
| Step 2. what you are looking for. | the number |
| Step 3. Choose a variable to represent the number. | Let [latex]n=\text{the number}[/latex] |
| Step 4. Restate as one sentence.Translate into an equation. | [latex]n-6\enspace\Rightarrow[/latex] The difference of a number and 6[latex]=\enspace\Rightarrow[/latex] is [latex]13\enspace\Rightarrow[/latex] thirteen |
| Step 5. the equation.Add 6 to both sides. Simplify. | [latex]n-6=13[/latex][latex]n-6\color{red}{+6}=13\color{red}{+6}[/latex] [latex]n=19[/latex] |
| Step 6. The difference of [latex]19[/latex] and [latex]6[/latex] is [latex]13[/latex]. It checks. | |
| Step 7. the question. | The number is [latex]19[/latex]. |
The sum of twice a number and seven is [latex]15[/latex]. Find the number.
Show Solution
| Step 1. the problem. | |
| Step 2. what you are looking for. | the number |
| Step 3. Choose a variable to represent the number. | Let [latex]n=\text{the number}[/latex] |
| Step 4. Restate the problem as one sentence.Translate into an equation. | [latex]2n\enspace\Rightarrow[/latex] The sum of twice a number[latex]+\enspace\Rightarrow[/latex] and [latex]7\enspace\Rightarrow[/latex] seven [latex]=\enspace\Rightarrow[/latex] is [latex]15\enspace\Rightarrow[/latex] fifteen |
| Step 5. the equation. | [latex]2n+7=15[/latex] |
| Subtract 7 from each side and simplify. | [latex]2n=8[/latex] |
| Divide each side by 2 and simplify. | [latex]n=4[/latex] |
| Step 6. is the sum of twice [latex]4[/latex] and [latex]7[/latex] equal to [latex]15[/latex]?[latex]2\cdot{4}+7=15[/latex] [latex]8+7=15[/latex] [latex]15=15\quad\checkmark[/latex] | |
| Step 7. the question. | The number is [latex]4[/latex]. |
Watch the following video to see another example of how to solve a number problem.
Solving for Two or More Numbers
Some number word problems ask you to find two or more numbers. It may be tempting to name them all with different variables, but so far we have only solved equations with one variable. We will define the numbers in terms of the same variable. Be sure to read the problem carefully to discover how all the numbers relate to each other.
One number is five more than another. The sum of the numbers is twenty-one. Find the numbers.
| Step 1. the problem. | ||
| Step 2. what you are looking for. | You are looking for two numbers. | |
| Step 3. Choose a variable to represent the first number. What do you know about the second number? Translate. | Let [latex]n=\text{1st number}[/latex]One number is five more than another. [latex]x+5={2}^{\text{nd}}\text{number}[/latex] | |
| Step 4. Restate the problem as one sentence with all the important information. Translate into an equation. Substitute the variable expressions. | The sum of the numbers is [latex]21[/latex].The sum of the 1st number and the 2nd number is [latex]21[/latex]. [latex]n\enspace\Rightarrow[/latex] First number [latex]+\enspace\Rightarrow[/latex] + [latex]n+5\enspace\Rightarrow[/latex] Second number [latex]=\enspace\Rightarrow[/latex] = [latex]21\enspace\Rightarrow[/latex] 21 | |
| Step 5. the equation. | [latex]n+n+5=21[/latex] | |
| Combine like terms. | [latex]2n+5=21[/latex] | |
| Subtract five from both sides and simplify. | [latex]2n=16[/latex] | |
| Divide by two and simplify. | [latex]n=8[/latex] 1st number | |
| Find the second number too. | [latex]n+5[/latex] 2nd number | |
| Substitute [latex]n = 8[/latex] | [latex]\color{red}{8}+5[/latex] | |
| [latex]13[/latex] | ||
| Step 6. | ||
| Do these numbers check in the problem?Is one number 5 more than the other? Is thirteen, 5 more than 8? Yes. Is the sum of the two numbers 21? | [latex]13\stackrel{\text{?}}{=}8+5[/latex][latex]13=13\quad\checkmark[/latex] [latex]8+13\stackrel{\text{?}}{=}21[/latex] [latex]21=21\quad\checkmark[/latex] | |
| Step 7. the question. | The numbers are [latex]8[/latex] and [latex]13[/latex]. |
Watch the following video to see another example of how to find two numbers given the relationship between the two.
The sum of two numbers is negative fourteen. One number is four less than the other. Find the numbers.
| Step 1. the problem. | ||
| Step 2. what you are looking for. | two numbers | |
| Step 3. Choose a variable.What do you know about the second number? Translate. | Let [latex]n=\text{1st number}[/latex]One number is [latex]4[/latex] less than the other. [latex]n-4={2}^{\text{nd}}\text{number}[/latex] | |
| Step 4. Write as one sentence. Translate into an equation. Substitute the variable expressions. | The sum of two numbers is negative fourteen.[latex]n\enspace\Rightarrow[/latex] First number [latex]+\enspace\Rightarrow[/latex] + [latex]n-4\enspace\Rightarrow[/latex] Second number [latex]=\enspace\Rightarrow[/latex] = [latex]-14\enspace\Rightarrow[/latex] -14 | |
| Step 5. the equation. | [latex]n+n-4=-14[/latex] | |
| Combine like terms. | [latex]2n-4=-14[/latex] | |
| Add 4 to each side and simplify. | [latex]2n=-10[/latex] | |
| Divide by 2. | [latex]n=-5[/latex] 1st number | |
| Substitute [latex]n=-5[/latex] to find the 2 number. | [latex]n-4[/latex] 2nd number | |
| [latex]\color{red}{-5}-4[/latex] | ||
| [latex]-9[/latex] | ||
| Step 6. | ||
| Is −9 four less than −5?Is their sum −14? | [latex]-5-4\stackrel{\text{?}}{=}-9[/latex][latex]-9=-9\quad\checkmark[/latex] [latex]-5+(-9)\stackrel{\text{?}}{=}-14[/latex] [latex]-14=-14\quad\checkmark[/latex] | |
| Step 7. the question. | The numbers are [latex]−5[/latex] and [latex]−9[/latex]. |
One number is ten more than twice another. Their sum is one. Find the numbers.
| Step 1. the problem. | ||
| Step 2. what you are looking for. | two numbers | |
| Step 3. Choose a variable.One number is ten more than twice another. | Let [latex]x=\text{1st number}[/latex][latex]2x+10={2}^{\text{nd}}\text{number}[/latex] | |
| Step 4. Restate as one sentence. | Their sum is one. | |
| Translate into an equation | [latex]x+(2x+10)\enspace\Rightarrow[/latex] The sum of the two numbers[latex]=\enspace\Rightarrow[/latex] is [latex]1\enspace\Rightarrow[/latex] 1 | |
| Step 5. the equation. | [latex]x+2x+10=1[/latex] | |
| Combine like terms. | [latex]3x+10=1[/latex] | |
| Subtract 10 from each side. | [latex]3x=-9[/latex] | |
| Divide each side by 3 to get the first number. | [latex]x=-3[/latex] | |
| Substitute to get the second number. | [latex]2x+10[/latex] | |
| [latex]2(\color{red}{-3})+10[/latex] | ||
| [latex]4[/latex] | ||
| Step 6. | ||
| Is 4 ten more than twice −3?Is their sum 1? | [latex]2(-3)+10\stackrel{\text{?}}{=}4[/latex][latex]-6+10=4[/latex] [latex]4=4\quad\checkmark[/latex] [latex]-3+4\stackrel{\text{?}}{=}1[/latex] [latex]1=1\quad\checkmark[/latex] | |
| Step 7. the question. | The numbers are [latex]−3[/latex] and [latex]4[/latex]. |
Solving for Consecutive Integers
Consecutive integers are integers that immediately follow each other. Some examples of consecutive integers are:
[latex]\begin{array}{c}\phantom{\rule{0.2em}{0ex}}\\ \phantom{\rule{0.2em}{0ex}}\\ \phantom{\rule{0.2em}{0ex}}\\ \phantom{\rule{0.2em}{0ex}}\\ \hfill \text{…}1,2,3,4\text{,…}\hfill \end{array}[/latex] [latex]\text{…}-10,-9,-8,-7\text{,…}[/latex] [latex]\text{…}150,151,152,153\text{,…}[/latex]
Notice that each number is one more than the number preceding it. So if we define the first integer as [latex]n[/latex], the next consecutive integer is [latex]n+1[/latex]. The one after that is one more than [latex]n+1[/latex], so it is [latex]n+1+1[/latex], or [latex]n+2[/latex].
[latex]\begin{array}{cccc}n\hfill & & & \text{1st integer}\hfill \\ n+1\hfill & & & \text{2nd consecutive integer}\hfill \\ n+2\hfill & & & \text{3rd consecutive integer}\hfill \end{array}[/latex]
The sum of two consecutive integers is [latex]47[/latex]. Find the numbers.
| Step 1. the problem. | ||
| Step 2. what you are looking for. | two consecutive integers | |
| Step 3. | Let [latex]n=\text{1st integer}[/latex][latex]n+1=\text{next consecutive integer}[/latex] | |
| Step 4. Restate as one sentence. Translate into an equation. | [latex]n+n+1\enspace\Rightarrow[/latex] The sum of the integers[latex]=\enspace\Rightarrow[/latex] is [latex]47\enspace\Rightarrow[/latex] 47 | |
| Step 5. the equation. | [latex]n+n+1=47[/latex] | |
| Combine like terms. | [latex]2n+1=47[/latex] | |
| Subtract 1 from each side. | [latex]2n=46[/latex] | |
| Divide each side by 2. | [latex]n=23[/latex] 1st integer | |
| Substitute to get the second number. | [latex]n+1[/latex] 2nd integer | |
| [latex]\color{red}{23}+1[/latex] | ||
| [latex]24[/latex] | ||
| Step 6. | [latex]23+24\stackrel{\text{?}}{=}47[/latex][latex]47=47\quad\checkmark[/latex] | |
| Step 7. the question. | The two consecutive integers are [latex]23[/latex] and [latex]24[/latex]. |
Find three consecutive integers whose sum is [latex]42[/latex].
| Step 1. the problem. | ||
| Step 2. what you are looking for. | three consecutive integers | |
| Step 3. | Let [latex]n=\text{1st integer}[/latex][latex]n+1=\text{2nd consecutive integer}[/latex] [latex]n+2=\text{3rd consecutive integer}[/latex]
| |
| Step 4. Restate as one sentence. Translate into an equation. | [latex]n\enspace +\enspace n+1\enspace +\enspace n+2\enspace\Rightarrow[/latex] The sum of the three integers[latex]=\enspace\Rightarrow[/latex] is [latex]42\enspace\Rightarrow[/latex] 42 | |
| Step 5. the equation. | [latex]n+n+1+n+2=42[/latex] | |
| Combine like terms. | [latex]3n+3=42[/latex] | |
| Subtract 3 from each side. | [latex]3n=39[/latex] | |
| Divide each side by 3. | [latex]n=13[/latex] 1st integer | |
| Substitute to get the second number. | [latex]n+1[/latex] 2nd integer | |
| [latex]\color{red}{13}+1[/latex] | ||
| [latex]24[/latex] | ||
| Substitute to get the third number. | [latex]n+2[/latex] 3rd integer | |
| [latex]\color{red}{13}+2[/latex] | ||
| [latex]15[/latex] | ||
| Step 6. | [latex]13+14+15\stackrel{\text{?}}{=}42[/latex][latex]42=42\quad\checkmark[/latex] | |
| Step 7. the question. | The three consecutive integers are [latex]13[/latex], [latex]14[/latex], and [latex]15[/latex]. |
Watch this video for another example of how to find three consecutive integers given their sum.
- Ex: Linear Equation Application with One Variable - Number Problem. Authored by : James Sousa (Mathispower4u.com). Located at : https://youtu.be/juslHscrh8s . License : CC BY: Attribution
- Ex: Write and Solve an Equation for Consecutive Natural Numbers with a Given Sum. Authored by : James Sousa (Mathispower4u.com). Located at : https://youtu.be/Bo67B0L9hGs . License : CC BY: Attribution
- Write and Solve a Linear Equations to Solve a Number Problem (1) Mathispower4u . Authored by : James Sousa (Mathispower4u.com) for Lumen Learning. Located at : https://youtu.be/izIIqOztUyI . License : CC BY: Attribution
- Question ID 142763, 142770, 142775, 142806, 142811, 142816, 142817. Authored by : Lumen Learning. License : CC BY: Attribution . License Terms : IMathAS Community License, CC-BY + GPL
- Prealgebra. Provided by : OpenStax. License : CC BY: Attribution . License Terms : Download for free at http://cnx.org/contents/[email protected]

Maths with David
Problem solving. simplify problem.
If a problem is too difficult to solve immediately, it can be valuable to solve a simpler problem instead, which can give us insight into the original problem. It typically won’t give us an answer, but can help us identify a suitable method.
We can simplify by replacing “difficult” numbers with simple round numbers to make calculation easier. Or we can replace a complex diagram with a simplified diagram that follows the same pattern.
Examples of using a diagram to tackle a problem
First we will read all three examples and have a quick think about them and then we will look at how simplifying the problem can help us with each one:
Counting Squares Example
How many squares (of any size) are there in the diagram below?

Climbing Stairs Example
Suzanne is climbing a flight of 10 stairs. She can either go from one stair to the next one (1 step), or she can miss out a stair and go up two at once (2 step). How many different ways can she go up the 10 stairs?
Factors Example
Find the smallest number that can be divided by all of the numbers from 1 to 20 without leaving a remainder.
Worked Solutions to Examples
We can consider progressively larger grids and look for a pattern. So we start with a 2×2 grid:

- 1 large 2×2 square and
- 4 small 1×1 squares.
We then consider a 3×3 grid:

- 1 large 3×3 square,
- 4 medium 2×2 squares and
- 9 small 1×1 squares.
And finally a 4×4 grid:

- 1 4×4 square,
- 4 3×3 squares,
- 9 2×2 squares.
You can probably notice a pattern from these examples. If you apply this pattern to the question, how many squares will there be in total?
Imagine first a staircase with only 1 stair, for which there will be only 1 way of climbing it, then one with 2 stairs for which their will be 2 ways, then one with 3 stairs for which there will be 3 ways. If we continue in this manner until we are considering a staircase with 10 squares, we find the following:
| 1 | 1 |
| 2 | 2 |
| 3 | 3 |
| 4 | 5 |
| 5 | 8 |
If we look carefully at the second column we may be able to recognise that it is a known sequence, the Fibonacci sequence. We could test this for 6 stairs to check whether 13 seems a suitable answer, and then we can extend the sequence up to 10 stairs.
Suppose it only had to be dividable by the number from 1 to 3. Then clearly this would have to be 6, as there is no smaller number which has factors 1, 2 and 3.
What if it was 1 to 4? Well, multiplying these numbers together gives 1 x 2 x 3 x 4 = 24. But this is not the smallest number with all these as factors. Because the 4 already has one 2 as a factor, we don’t need to include that 2 twice and so we can take 2 x 3 x 2 = 12.
What if it was 1 to 5? Well we found above that 12 is divisible by 1 to 4. But it isn’t divisible by 5, so we will have to multiply this by 5 to give 60. You many notice that it matters whether the number is a prime or a composite number.
What if it was 1 to 6? Well, we already found that 60 is divisible by 1 to 5, and it is also divisible by 6, so this is the smallest number.
What if it was 1 to 7? As 7 is a prime we must multiply this to give 60 x 7 = 420.
For 1 to 8 we only need one extra 2 because our number is already divisible by 4, so we have 60 x 7 x 2 = 840
For 1 to 9 we only need one extra 3 because our number is already divisible by 3, so we have 60 x 7 x 2 x 8 = 2520.
For 1 to 10 we notice that 2520 is already divisible by 10. So written as a product of primes, our number is now 2 x 2 x 2 x 3 x 3 x 5 x 7
We then carry on with the same logic through the numbers from 11 to 20 to find out what our “smallest possible number” must be multiplied by in order to have these as factors, as shown below.
| 11 | Need to multiply by it, it is prime | 16 | We already have 8 (i.e. 2 x 2 x 2 above), but need an extra 2 |
| 12 | Already included (i.e. 2 x 2 x 3 above) | 17 | Need to multiply by it, it is prime |
| 13 | Need to multiply by it, it is prime | 18 | Already included (i.e. 2 x 2 x 3 x 3 above) |
| 14 | Already included (i.e. 2 x 7 above) | 19 | Need to multiply by it, it is prime |
| 15 | Already included (i.e. 3 x 5 above) | 20 | Already included (i.e. 2 x 2 x 5 above) |
So from the table we have additional factors, of 11, 13, 2, 17 and 19 to multiply by, biving us the final product of 2 x 2 x 2 x 2 x 3 x 3 x 5 x 7 x 11 x 13 x 17 x 19. This equals 232,792,560.
17 Questions of Increasing Difficulty

Worked Solutions to Questions

Share this:

- Already have a WordPress.com account? Log in now.
- Subscribe Subscribed
- Copy shortlink
- Report this content
- View post in Reader
- Manage subscriptions
- Collapse this bar
2.2 Use a Problem Solving Strategy
Learning objectives.
- Use a problem solving strategy for word problems
- Solve number word problems
- Solve percent applications
- Solve simple interest applications

Be Prepared 2.2
Before you get started, take this readiness quiz.
- Translate “six less than twice x ” into an algebraic expression. If you missed this problem, review Example 1.8 .
- Convert 4.5% to a decimal. If you missed this problem, review Example 1.40 .
- Convert 0.6 to a percent. If you missed this problem, review Example 1.40 .
Have you ever had any negative experiences in the past with word problems? When we feel we have no control, and continue repeating negative thoughts, we set up barriers to success. Realize that your negative experiences with word problems are in your past. To move forward you need to calm your fears and change your negative feelings.
Start with a fresh slate and begin to think positive thoughts. Repeating some of the following statements may be helpful to turn your thoughts positive. Thinking positive thoughts is a first step towards success.
I think I can! I think I can!
While word problems were hard in the past, I think I can try them now.
I am better prepared now—I think I will begin to understand word problems.
I am able to solve equations because I practiced many problems and I got help when I needed it—I can try that with word problems.
It may take time, but I can begin to solve word problems.
You are now well prepared and you are ready to succeed. If you take control and believe you can be successful, you will be able to master word problems.
Use a Problem Solving Strategy for Word Problems
Now that we can solve equations, we are ready to apply our new skills to word problems. We will develop a strategy we can use to solve any word problem successfully.
Example 2.14
Normal yearly snowfall at the local ski resort is 12 inches more than twice the amount it received last season. The normal yearly snowfall is 62 inches. What was the snowfall last season at the ski resort?
| the problem. | |
| what you are looking for. | What was the snowfall last season? |
| what we are looking for and choose a variable to represent it. | Let the snowfall last season. |
| Restate the problem in one sentence with all the important information. | |
| Translate into an equation. | |
| the equation. | |
| Subtract 12 from each side. | |
| Simplify. | |
| Divide each side by two. | |
| Simplify. | |
| First, is our answer reasonable? Yes, having 25 inches of snow seems OK. The problem says the normal snowfall is twelve inches more than twice the number of last season. Twice 25 is 50 and 12 more than that is 62. | |
| the question. | The snowfall last season was 25 inches. |
Try It 2.27
Guillermo bought textbooks and notebooks at the bookstore. The number of textbooks was three more than twice the number of notebooks. He bought seven textbooks. How many notebooks did he buy?
Try It 2.28
Gerry worked Sudoku puzzles and crossword puzzles this week. The number of Sudoku puzzles he completed is eight more than twice the number of crossword puzzles. He completed 22 Sudoku puzzles. How many crossword puzzles did he do?
We summarize an effective strategy for problem solving.
Use a Problem Solving Strategy for word problems.
- Step 1. Read the problem. Make sure all the words and ideas are understood.
- Step 2. Identify what you are looking for.
- Step 3. Name what you are looking for. Choose a variable to represent that quantity.
- Step 4. Translate into an equation. It may be helpful to restate the problem in one sentence with all the important information. Then, translate the English sentence into an algebra equation.
- Step 5. Solve the equation using proper algebra techniques.
- Step 6. Check the answer in the problem to make sure it makes sense.
- Step 7. Answer the question with a complete sentence.
Solve Number Word Problems
We will now apply the problem solving strategy to “number word problems.” Number word problems give some clues about one or more numbers and we use these clues to write an equation. Number word problems provide good practice for using the Problem Solving Strategy.
Example 2.15
The sum of seven times a number and eight is thirty-six. Find the number.
| the problem. | |
| what you are looking for. | the number |
| what you are looking for and choose a variable to represent it. | Let = the number. |
| Restate the problem as one sentence. Translate into an equation. | |
| the equation. Subtract eight from each side and simplify. Divide each side by seven and simplify. | |
| Is the sum of seven times four plus eight equal to 36? | |
| the question. | The number is 4. |
Did you notice that we left out some of the steps as we solved this equation? If you’re not yet ready to leave out these steps, write down as many as you need.
Try It 2.29
The sum of four times a number and two is fourteen. Find the number.
Try It 2.30
The sum of three times a number and seven is twenty-five. Find the number.
Some number word problems ask us to find two or more numbers. It may be tempting to name them all with different variables, but so far, we have only solved equations with one variable. In order to avoid using more than one variable, we will define the numbers in terms of the same variable. Be sure to read the problem carefully to discover how all the numbers relate to each other.
Example 2.16
The sum of two numbers is negative fifteen. One number is nine less than the other. Find the numbers.
| the problem. | |
| what you are looking for. | two numbers |
| what you are looking for by choosing a variable to represent the first number. “One number is nine less than the other.” | Let number. number |
| Write as one sentence. Translate into an equation. | The sum of two numbers is negative fifteen. |
| the equation. Combine like terms. Add nine to each side and simplify. Simplify. | |
| Is nine less than Is their sum | |
| the question. | The numbers are and |
Try It 2.31
The sum of two numbers is negative twenty-three. One number is seven less than the other. Find the numbers.
Try It 2.32
The sum of two numbers is negative eighteen. One number is forty more than the other. Find the numbers.
Some number problems involve consecutive integers . Consecutive integers are integers that immediately follow each other. Examples of consecutive integers are:
Notice that each number is one more than the number preceding it. Therefore, if we define the first integer as n , the next consecutive integer is n + 1 . n + 1 . The one after that is one more than n + 1 , n + 1 , so it is n + 1 + 1 , n + 1 + 1 , which is n + 2 . n + 2 .
We will use this notation to represent consecutive integers in the next example.
Example 2.17
Find three consecutive integers whose sum is −54 . −54 .
| the problem. | |
| what you are looking for. | three consecutive integers |
| each of the three numbers | Let integer. consecutive integer consecutive integer |
| Restate as one sentence. Translate into an equation. | The sum of the three integers is |
| the equation. Combine like terms. Subtract three from each side. Divide each side by three. | |
| | |
| the question. | The three consecutive integers are and |
Try It 2.33
Find three consecutive integers whose sum is −96 . −96 .
Try It 2.34
Find three consecutive integers whose sum is −36 . −36 .
Now that we have worked with consecutive integers, we will expand our work to include consecutive even integers and consecutive odd integers . Consecutive even integers are even integers that immediately follow one another. Examples of consecutive even integers are:
Notice each integer is two more than the number preceding it. If we call the first one n , then the next one is n + 2 . n + 2 . The one after that would be n + 2 + 2 n + 2 + 2 or n + 4 . n + 4 .
Consecutive odd integers are odd integers that immediately follow one another. Consider the consecutive odd integers 63, 65, and 67.
Does it seem strange to have to add two (an even number) to get the next odd number? Do we get an odd number or an even number when we add 2 to 3? to 11? to 47?
Whether the problem asks for consecutive even numbers or odd numbers, you do not have to do anything different. The pattern is still the same—to get to the next odd or the next even integer, add two.
Example 2.18
Find three consecutive even integers whose sum is 120 120 .
Step 1. Read the problem. Step 2. Identify what you are looking for. three consecutive even integers Step 3. Name. Let n = 1 st even integer. n + 2 = 2 nd consecutive even integer n + 4 = 3 rd consecutive even integer Step 4. Translate. Restate as one sentence. The sum of the three even integers is 120 . Translate into an equation. n + n + 2 + n + 4 = 120 Step 5. Solve the equation. n + n + 2 + n + 4 = 120 Combine like terms. 3 n + 6 = 120 Subtract 6 from each side. 3 n = 114 Divide each side by 3. n = 38 1 st integer n + 2 2 nd integer 38 + 2 40 n + 4 3 rd integer 38 + 4 42 Step 6. Check. 38 + 40 + 42 = ? 120 120 = 120 ✓ Step 7. Answer the question. The three consecutive integers are 38, 40, and 42. Step 1. Read the problem. Step 2. Identify what you are looking for. three consecutive even integers Step 3. Name. Let n = 1 st even integer. n + 2 = 2 nd consecutive even integer n + 4 = 3 rd consecutive even integer Step 4. Translate. Restate as one sentence. The sum of the three even integers is 120 . Translate into an equation. n + n + 2 + n + 4 = 120 Step 5. Solve the equation. n + n + 2 + n + 4 = 120 Combine like terms. 3 n + 6 = 120 Subtract 6 from each side. 3 n = 114 Divide each side by 3. n = 38 1 st integer n + 2 2 nd integer 38 + 2 40 n + 4 3 rd integer 38 + 4 42 Step 6. Check. 38 + 40 + 42 = ? 120 120 = 120 ✓ Step 7. Answer the question. The three consecutive integers are 38, 40, and 42.
Try It 2.35
Find three consecutive even integers whose sum is 102.
Try It 2.36
Find three consecutive even integers whose sum is −24 . −24 .
When a number problem is in a real life context, we still use the same strategies that we used for the previous examples.
Example 2.19
A married couple together earns $110,000 a year. The wife earns $16,000 less than twice what her husband earns. What does the husband earn?
Step 1. Read the problem. Step 2. Identify what you are looking for. How much does the husband earn? Step 3. Name. Choose a variable to represent Let h = the amount the husband earns. the amount the husband earns. The wife earns $16,000 less than twice that. Step 4. Translate. Restate the problem in one sentence with all the important information. Translate into an equation. 2 h − 16,000 = the amount the wife earns Together the husband and wife earn $110,000. h + 2 h − 16,000 = 110,000 Step 5. Solve the equation. Combine like terms. Add 16,000 to both sides and simplify. Divide each side by three. h + 2 h − 16,000 = 110,000 3 h − 16,000 = 110,000 3 h = 126,000 h = 42,000 $42,000 amount husband earns 2 h − 16,000 amount wife earns 2 ( 42,000 ) − 16,000 84,000 − 16,000 68,000 Step 6. Check: If the wife earns $68,000 and the husband earns $42,000, is that $110,000? Yes! Step 7. Answer the question. The husband earns $42,000 a year. Step 1. Read the problem. Step 2. Identify what you are looking for. How much does the husband earn? Step 3. Name. Choose a variable to represent Let h = the amount the husband earns. the amount the husband earns. The wife earns $16,000 less than twice that. Step 4. Translate. Restate the problem in one sentence with all the important information. Translate into an equation. 2 h − 16,000 = the amount the wife earns Together the husband and wife earn $110,000. h + 2 h − 16,000 = 110,000 Step 5. Solve the equation. Combine like terms. Add 16,000 to both sides and simplify. Divide each side by three. h + 2 h − 16,000 = 110,000 3 h − 16,000 = 110,000 3 h = 126,000 h = 42,000 $42,000 amount husband earns 2 h − 16,000 amount wife earns 2 ( 42,000 ) − 16,000 84,000 − 16,000 68,000 Step 6. Check: If the wife earns $68,000 and the husband earns $42,000, is that $110,000? Yes! Step 7. Answer the question. The husband earns $42,000 a year.
Try It 2.37
According to the National Automobile Dealers Association, the average cost of a car in 2014 was $28,400. This was $1,600 less than six times the cost in 1975. What was the average cost of a car in 1975?
Try It 2.38
US Census data shows that the median price of new home in the U.S. in November 2014 was $280,900. This was $10,700 more than 14 times the price in November 1964. What was the median price of a new home in November 1964?
Solve Percent Applications
There are several methods to solve percent equations. In algebra, it is easiest if we just translate English sentences into algebraic equations and then solve the equations. Be sure to change the given percent to a decimal before you use it in the equation.
Example 2.20
Translate and solve:
ⓐ What number is 45% of 84? ⓑ 8.5% of what amount is $4.76? ⓒ 168 is what percent of 112?
| Translate into algebra. Let the number. | |||
| Multiply. | |||
| 37.8 is 45% of 84. |
| Translate. Let the amount. | |||
| Multiply. | |||
| Divide both sides by 0.085 and simplify. | |||
| 8.5% of $56 is $4.76 |
| We are asked to find percent, so we must have our result in percent form. | |||
| Translate into algebra. Let = the percent. | |||
| Multiply. | |||
| Divide both sides by 112 and simplify. | |||
| Convert to percent. | |||
| 168 is 150% of 112. |
Try It 2.39
Translate and solve: ⓐ What number is 45% of 80? ⓑ 7.5% of what amount is $1.95? ⓒ 110 is what percent of 88?
Try It 2.40
Translate and solve: ⓐ What number is 55% of 60? ⓑ 8.5% of what amount is $3.06? ⓐ 126 is what percent of 72?
Now that we have a problem solving strategy to refer to, and have practiced solving basic percent equations, we are ready to solve percent applications. Be sure to ask yourself if your final answer makes sense—since many of the applications we will solve involve everyday situations, you can rely on your own experience.
Example 2.21
The label on Audrey’s yogurt said that one serving provided 12 grams of protein, which is 24% of the recommended daily amount. What is the total recommended daily amount of protein?
| What are you asked to find? | What total amount of protein is recommended? |
| Choose a variable to represent it. | Let total amount of protein. |
| Write a sentence that gives the information to find it. | |
| Translate into an equation. | |
| Solve. | |
| Check: Does this make sense? Yes, 24% is about of the total and 12 is about of 50. | |
| Write a complete sentence to answer the question. | The amount of protein that is recommended is 50 g. |
Try It 2.41
One serving of wheat square cereal has 7 grams of fiber, which is 28% of the recommended daily amount. What is the total recommended daily amount of fiber?
Try It 2.42
One serving of rice cereal has 190 mg of sodium, which is 8% of the recommended daily amount. What is the total recommended daily amount of sodium?
Remember to put the answer in the form requested. In the next example we are looking for the percent.
Example 2.22
Veronica is planning to make muffins from a mix. The package says each muffin will be 240 calories and 60 calories will be from fat. What percent of the total calories is from fat?
| What are you asked to find? | What percent of the total calories is fat? |
| Choose a variable to represent it. | Let percent of fat. |
| Write a sentence that gives the information to find it. | |
| Translate the sentence into an equation. | |
| Multiply. | |
| Divide both sides by 240. | |
| Put in percent form. | |
| Check: does this make sense? Yes, is one-fourth; 60 is one-fourth of 240. So, makes sense. | |
| Write a complete sentence to answer the question. | Of the total calories in each muffin, is fat. |
Try It 2.43
Mitzi received some gourmet brownies as a gift. The wrapper said each 28% brownie was 480 calories, and had 240 calories of fat. What percent of the total calories in each brownie comes from fat? Round the answer to the nearest whole percent.
Try It 2.44
The mix Ricardo plans to use to make brownies says that each brownie will be 190 calories, and 76 calories are from fat. What percent of the total calories are from fat? Round the answer to the nearest whole percent.
It is often important in many fields—business, sciences, pop culture—to talk about how much an amount has increased or decreased over a certain period of time. This increase or decrease is generally expressed as a percent and called the percent change .
To find the percent change, first we find the amount of change, by finding the difference of the new amount and the original amount. Then we find what percent the amount of change is of the original amount.
Find percent change.
- Step 1. Find the amount of change. change = new amount − original amount change = new amount − original amount
- Step 2. Find what percent the amount of change is of the original amount. change is what percent of the original amount? change is what percent of the original amount?
Example 2.23
Recently, the California governor proposed raising community college fees from $36 a unit to $46 a unit. Find the percent change. (Round to the nearest tenth of a percent.)
| Find the amount of change. | |
| Find the percent. | Change is what percent of the original amount? |
| Let the percent. | |
| Translate to an equation. | |
| Simplify. | |
| Divide both sides by 36. | |
| Change to percent form; round to the nearest tenth | |
| Write a complete sentence to answer the question. | The new fees are approximately a increase over the old fees. |
| Remember to round the division to the nearest thousandth in order to round the percent to the nearest tenth. | |
Try It 2.45
Find the percent change. (Round to the nearest tenth of a percent.) In 2011, the IRS increased the deductible mileage cost to 55.5 cents from 51 cents.
Try It 2.46
Find the percent change. (Round to the nearest tenth of a percent.) In 1995, the standard bus fare in Chicago was $1.50. In 2008, the standard bus fare was 2.25.
Applications of discount and mark-up are very common in retail settings.
When you buy an item on sale, the original price has been discounted by some dollar amount. The discount rate , usually given as a percent, is used to determine the amount of the discount. To determine the amount of discount , we multiply the discount rate by the original price.
The price a retailer pays for an item is called the original cost . The retailer then adds a mark-up to the original cost to get the list price , the price he sells the item for. The mark-up is usually calculated as a percent of the original cost. To determine the amount of mark-up, multiply the mark-up rate by the original cost.
The sale price should always be less than the original price.
The list price should always be more than the original cost.
Example 2.24
Liam’s art gallery bought a painting at an original cost of $750. Liam marked the price up 40%. Find ⓐ the amount of mark-up and ⓑ the list price of the painting.
| Identify what you are asked to find, and choose a variable to represent it. | What is the amount of mark-up? Let the amount of mark-up. |
| Write a sentence that gives the information to find it. | |
| Translate into an equation. | |
| Solve the equation. | |
| Write a complete sentence. | The mark-up on the painting was $300. |
| Identify what you are asked to find, and choose a variable to represent it. | What is the list price? Let the list price. |
| Write a sentence that gives the information to find it. | |
| Translate into an equation. | |
| Solve the equation. | |
| Check. | Is the list price more than the original cost? Is $1,050 more than $750? Yes. |
| Write a complete sentence. | The list price of the painting was $1,050. |
Try It 2.47
Find ⓐ the amount of mark-up and ⓑ the list price: Jim’s music store bought a guitar at original cost $1,200. Jim marked the price up 50%.
Try It 2.48
Find ⓐ the amount of mark-up and ⓑ the list price: The Auto Resale Store bought Pablo’s Toyota for $8,500. They marked the price up 35%.
Solve Simple Interest Applications
Interest is a part of our daily lives. From the interest earned on our savings to the interest we pay on a car loan or credit card debt, we all have some experience with interest in our lives.
The amount of money you initially deposit into a bank is called the principal , P , and the bank pays you interest , I. When you take out a loan, you pay interest on the amount you borrow, also called the principal.
In either case, the interest is computed as a certain percent of the principal, called the rate of interest , r . The rate of interest is usually expressed as a percent per year, and is calculated by using the decimal equivalent of the percent. The variable t , (for time) represents the number of years the money is saved or borrowed.
Interest is calculated as simple interest or compound interest. Here we will use simple interest.
Simple Interest
If an amount of money, P , called the principal, is invested or borrowed for a period of t years at an annual interest rate r , the amount of interest, I , earned or paid is
Interest earned or paid according to this formula is called simple interest .
The formula we use to calculate interest is I = P r t . I = P r t . To use the formula we substitute in the values for variables that are given, and then solve for the unknown variable. It may be helpful to organize the information in a chart.
Example 2.25
Areli invested a principal of $950 in her bank account that earned simple interest at an interest rate of 3%. How much interest did she earn in five years?
I = ? P = $ 950 r = 3 % t = 5 years I = ? P = $ 950 r = 3 % t = 5 years
Identify what you are asked to find, and choose a What is the simple interest? variable to represent it. Let I = interest. Write the formula. I = P r t Substitute in the given information. I = ( 950 ) ( 0.03 ) ( 5 ) Simplify. I = 142.5 Check. Is $142.50 a reasonable amount of interest on $950? Yes. Write a complete sentence. The interest is $142.50. Identify what you are asked to find, and choose a What is the simple interest? variable to represent it. Let I = interest. Write the formula. I = P r t Substitute in the given information. I = ( 950 ) ( 0.03 ) ( 5 ) Simplify. I = 142.5 Check. Is $142.50 a reasonable amount of interest on $950? Yes. Write a complete sentence. The interest is $142.50.
Try It 2.49
Nathaly deposited $12,500 in her bank account where it will earn 4% simple interest. How much interest will Nathaly earn in five years?
Try It 2.50
Susana invested a principal of $36,000 in her bank account that earned simple interest at an interest rate of 6.5 % . 6.5 % . How much interest did she earn in three years?
There may be times when we know the amount of interest earned on a given principal over a certain length of time, but we do not know the rate.
Example 2.26
Hang borrowed $7,500 from her parents to pay her tuition. In five years, she paid them $1,500 interest in addition to the $7,500 she borrowed. What was the rate of simple interest?
I = $ 1500 P = $ 7500 r = ? t = 5 years I = $ 1500 P = $ 7500 r = ? t = 5 years
Identify what you are asked to find, and choose What is the rate of simple interest? a variable to represent it. Write the formula. Substitute in the given information. Multiply. Divide. Change to percent form. Let r = rate of interest. I = P r t 1,500 = ( 7,500 ) r ( 5 ) 1,500 = 37,500 r 0.04 = r 4 % = r Check. I = P r t 1,500 = ? ( 7,500 ) ( 0.04 ) ( 5 ) 1,500 = 1,500 ✓ Write a complete sentence. The rate of interest was 4%. Identify what you are asked to find, and choose What is the rate of simple interest? a variable to represent it. Write the formula. Substitute in the given information. Multiply. Divide. Change to percent form. Let r = rate of interest. I = P r t 1,500 = ( 7,500 ) r ( 5 ) 1,500 = 37,500 r 0.04 = r 4 % = r Check. I = P r t 1,500 = ? ( 7,500 ) ( 0.04 ) ( 5 ) 1,500 = 1,500 ✓ Write a complete sentence. The rate of interest was 4%.
Try It 2.51
Jim lent his sister $5,000 to help her buy a house. In three years, she paid him the $5,000, plus $900 interest. What was the rate of simple interest?
Try It 2.52
Loren lent his brother $3,000 to help him buy a car. In four years, his brother paid him back the $3,000 plus $660 in interest. What was the rate of simple interest?
In the next example, we are asked to find the principal—the amount borrowed.
Example 2.27
Sean’s new car loan statement said he would pay $4,866,25 in interest from a simple interest rate of 8.5% over five years. How much did he borrow to buy his new car?
I = 4,866.25 P = ? r = 8.5 % t = 5 years I = 4,866.25 P = ? r = 8.5 % t = 5 years
Identify what you are asked to find, What is the amount borrowed (the principal)? and choose a variable to represent it. Write the formula. Substitute in the given information. Multiply. Divide. Let P = principal borrowed. I = P r t 4,866.25 = P ( 0.085 ) ( 5 ) 4,866.25 = 0.425 P 11,450 = P Check. I = P r t 4,866.25 = ? ( 11,450 ) ( 0.085 ) ( 5 ) 4,866.25 = 4,866.25 ✓ Write a complete sentence. The principal was $11,450. Identify what you are asked to find, What is the amount borrowed (the principal)? and choose a variable to represent it. Write the formula. Substitute in the given information. Multiply. Divide. Let P = principal borrowed. I = P r t 4,866.25 = P ( 0.085 ) ( 5 ) 4,866.25 = 0.425 P 11,450 = P Check. I = P r t 4,866.25 = ? ( 11,450 ) ( 0.085 ) ( 5 ) 4,866.25 = 4,866.25 ✓ Write a complete sentence. The principal was $11,450.
Try It 2.53
Eduardo noticed that his new car loan papers stated that with a 7.5% simple interest rate, he would pay $6,596.25 in interest over five years. How much did he borrow to pay for his car?
Try It 2.54
In five years, Gloria’s bank account earned $2,400 interest at 5% simple interest. How much had she deposited in the account?
Access this online resource for additional instruction and practice with using a problem solving strategy.
- Begining Arithmetic Problems
Section 2.2 Exercises
Practice makes perfect.
List five positive thoughts you can say to yourself that will help you approach word problems with a positive attitude. You may want to copy them on a sheet of paper and put it in the front of your notebook, where you can read them often.
List five negative thoughts that you have said to yourself in the past that will hinder your progress on word problems. You may want to write each one on a small piece of paper and rip it up to symbolically destroy the negative thoughts.
In the following exercises, solve using the problem solving strategy for word problems. Remember to write a complete sentence to answer each question.
There are 16 girls in a school club. The number of girls is four more than twice the number of boys. Find the number of boys.
There are 18 Cub Scouts in Troop 645. The number of scouts is three more than five times the number of adult leaders. Find the number of adult leaders.
Huong is organizing paperback and hardback books for her club’s used book sale. The number of paperbacks is 12 less than three times the number of hardbacks. Huong had 162 paperbacks. How many hardback books were there?
Jeff is lining up children’s and adult bicycles at the bike shop where he works. The number of children’s bicycles is nine less than three times the number of adult bicycles. There are 42 adult bicycles. How many children’s bicycles are there?
In the following exercises, solve each number word problem.
The difference of a number and 12 is three. Find the number.
The difference of a number and eight is four. Find the number.
The sum of three times a number and eight is 23. Find the number.
The sum of twice a number and six is 14. Find the number.
The difference of twice a number and seven is 17. Find the number.
The difference of four times a number and seven is 21. Find the number.
Three times the sum of a number and nine is 12. Find the number.
Six times the sum of a number and eight is 30. Find the number.
One number is six more than the other. Their sum is 42. Find the numbers.
One number is five more than the other. Their sum is 33. Find the numbers.
The sum of two numbers is 20. One number is four less than the other. Find the numbers.
The sum of two numbers is 27. One number is seven less than the other. Find the numbers.
One number is 14 less than another. If their sum is increased by seven, the result is 85. Find the numbers.
One number is 11 less than another. If their sum is increased by eight, the result is 71. Find the numbers.
The sum of two numbers is 14. One number is two less than three times the other. Find the numbers.
The sum of two numbers is zero. One number is nine less than twice the other. Find the numbers.
The sum of two consecutive integers is 77. Find the integers.
The sum of two consecutive integers is 89. Find the integers.
The sum of three consecutive integers is 78. Find the integers.
The sum of three consecutive integers is 60. Find the integers.
Find three consecutive integers whose sum is −3 . −3 .
Find three consecutive even integers whose sum is 258.
Find three consecutive even integers whose sum is 222.
Find three consecutive odd integers whose sum is −213 . −213 .
Find three consecutive odd integers whose sum is −267 . −267 .
Philip pays $1,620 in rent every month. This amount is $120 more than twice what his brother Paul pays for rent. How much does Paul pay for rent?
Marc just bought an SUV for $54,000. This is $7,400 less than twice what his wife paid for her car last year. How much did his wife pay for her car?
Laurie has $46,000 invested in stocks and bonds. The amount invested in stocks is $8,000 less than three times the amount invested in bonds. How much does Laurie have invested in bonds?
Erica earned a total of $50,450 last year from her two jobs. The amount she earned from her job at the store was $1,250 more than three times the amount she earned from her job at the college. How much did she earn from her job at the college?
In the following exercises, translate and solve.
ⓐ What number is 45% of 120? ⓑ 81 is 75% of what number? ⓐ What percent of 260 is 78?
ⓐ What number is 65% of 100? ⓑ 93 is 75% of what number? ⓐ What percent of 215 is 86?
ⓐ 250% of 65 is what number? ⓑ 8.2% of what amount is $2.87? ⓐ 30 is what percent of 20?
ⓐ 150% of 90 is what number? ⓑ 6.4% of what amount is $2.88? ⓐ 50 is what percent of 40?
In the following exercises, solve.
Geneva treated her parents to dinner at their favorite restaurant. The bill was $74.25. Geneva wants to leave 16% of the total bill as a tip. How much should the tip be?
When Hiro and his co-workers had lunch at a restaurant near their work, the bill was $90.50. They want to leave 18% of the total bill as a tip. How much should the tip be?
One serving of oatmeal has 8 grams of fiber, which is 33% of the recommended daily amount. What is the total recommended daily amount of fiber?
One serving of trail mix has 67 grams of carbohydrates, which is 22% of the recommended daily amount. What is the total recommended daily amount of carbohydrates?
A bacon cheeseburger at a popular fast food restaurant contains 2070 milligrams (mg) of sodium, which is 86% of the recommended daily amount. What is the total recommended daily amount of sodium?
A grilled chicken salad at a popular fast food restaurant contains 650 milligrams (mg) of sodium, which is 27% of the recommended daily amount. What is the total recommended daily amount of sodium?
The nutrition fact sheet at a fast food restaurant says the fish sandwich has 380 calories, and 171 calories are from fat. What percent of the total calories is from fat?
The nutrition fact sheet at a fast food restaurant says a small portion of chicken nuggets has 190 calories, and 114 calories are from fat. What percent of the total calories is from fat?
Emma gets paid $3,000 per month. She pays $750 a month for rent. What percent of her monthly pay goes to rent?
Dimple gets paid $3,200 per month. She pays $960 a month for rent. What percent of her monthly pay goes to rent?
Tamanika received a raise in her hourly pay, from $15.50 to $17.36. Find the percent change.
Ayodele received a raise in her hourly pay, from $24.50 to $25.48. Find the percent change.
Annual student fees at the University of California rose from about $4,000 in 2000 to about $12,000 in 2010. Find the percent change.
The price of a share of one stock rose from $12.50 to $50. Find the percent change.
A grocery store reduced the price of a loaf of bread from $2.80 to $2.73. Find the percent change.
The price of a share of one stock fell from $8.75 to $8.54. Find the percent change.
Hernando’s salary was $49,500 last year. This year his salary was cut to $44,055. Find the percent change.
In ten years, the population of Detroit fell from 950,000 to about 712,500. Find the percent change.
In the following exercises, find ⓐ the amount of discount and ⓑ the sale price.
Janelle bought a beach chair on sale at 60% off. The original price was $44.95.
Errol bought a skateboard helmet on sale at 40% off. The original price was $49.95.
In the following exercises, find ⓐ the amount of discount and ⓑ the discount rate (Round to the nearest tenth of a percent if needed.)
Larry and Donna bought a sofa at the sale price of $1,344. The original price of the sofa was $1,920.
Hiroshi bought a lawnmower at the sale price of $240. The original price of the lawnmower is $300.
In the following exercises, find ⓐ the amount of the mark-up and ⓑ the list price.
Daria bought a bracelet at original cost $16 to sell in her handicraft store. She marked the price up 45%. What was the list price of the bracelet?
Regina bought a handmade quilt at original cost $120 to sell in her quilt store. She marked the price up 55%. What was the list price of the quilt?
Tom paid $0.60 a pound for tomatoes to sell at his produce store. He added a 33% mark-up. What price did he charge his customers for the tomatoes?
Flora paid her supplier $0.74 a stem for roses to sell at her flower shop. She added an 85% mark-up. What price did she charge her customers for the roses?
Casey deposited $1,450 in a bank account that earned simple interest at an interest rate of 4%. How much interest was earned in two years?
Terrence deposited $5,720 in a bank account that earned simple interest at an interest rate of 6%. How much interest was earned in four years?
Robin deposited $31,000 in a bank account that earned simple interest at an interest rate of 5.2%. How much interest was earned in three years?
Carleen deposited $16,400 in a bank account that earned simple interest at an interest rate of 3.9% How much interest was earned in eight years?
Hilaria borrowed $8,000 from her grandfather to pay for college. Five years later, she paid him back the $8,000, plus $1,200 interest. What was the rate of simple interest?
Kenneth lent his niece $1,200 to buy a computer. Two years later, she paid him back the $1,200, plus $96 interest. What was the rate of simple interest?
Lebron lent his daughter $20,000 to help her buy a condominium. When she sold the condominium four years later, she paid him the $20,000, plus $3,000 interest. What was the rate of simple interest?
Pablo borrowed $50,000 to start a business. Three years later, he repaid the $50,000, plus $9,375 interest. What was the rate of simple interest?
In 10 years, a bank account that paid 5.25% simple interest earned $18,375 interest. What was the principal of the account?
In 25 years, a bond that paid 4.75% simple interest earned $2,375 interest. What was the principal of the bond?
Joshua’s computer loan statement said he would pay $1,244.34 in simple interest for a three-year loan at 12.4%. How much did Joshua borrow to buy the computer?
Margaret’s car loan statement said she would pay $7,683.20 in simple interest for a five-year loan at 9.8%. How much did Margaret borrow to buy the car?
Everyday Math
Tipping At the campus coffee cart, a medium coffee costs $1.65. MaryAnne brings $2.00 with her when she buys a cup of coffee and leaves the change as a tip. What percent tip does she leave?
Tipping Four friends went out to lunch and the bill came to $53.75 They decided to add enough tip to make a total of $64, so that they could easily split the bill evenly among themselves. What percent tip did they leave?
Writing Exercises
What has been your past experience solving word problems? Where do you see yourself moving forward?
Without solving the problem “44 is 80% of what number” think about what the solution might be. Should it be a number that is greater than 44 or less than 44? Explain your reasoning.
After returning from vacation, Alex said he should have packed 50% fewer shorts and 200% more shirts. Explain what Alex meant.
Because of road construction in one city, commuters were advised to plan that their Monday morning commute would take 150% of their usual commuting time. Explain what this means.
ⓐ After completing the exercises, use this checklist to evaluate your mastery of the objective of this section.
ⓑ After reviewing this checklist, what will you do to become confident for all objectives?
This book may not be used in the training of large language models or otherwise be ingested into large language models or generative AI offerings without OpenStax's permission.
Want to cite, share, or modify this book? This book uses the Creative Commons Attribution License and you must attribute OpenStax.
Access for free at https://openstax.org/books/intermediate-algebra/pages/1-introduction
- Authors: Lynn Marecek
- Publisher/website: OpenStax
- Book title: Intermediate Algebra
- Publication date: Mar 14, 2017
- Location: Houston, Texas
- Book URL: https://openstax.org/books/intermediate-algebra/pages/1-introduction
- Section URL: https://openstax.org/books/intermediate-algebra/pages/2-2-use-a-problem-solving-strategy
© Feb 9, 2022 OpenStax. Textbook content produced by OpenStax is licensed under a Creative Commons Attribution License . The OpenStax name, OpenStax logo, OpenStax book covers, OpenStax CNX name, and OpenStax CNX logo are not subject to the Creative Commons license and may not be reproduced without the prior and express written consent of Rice University.

- $ 0.00 0 items
Use a Problem Solving Strategy
2.2 use a solving problem strategy.
Topics covered in this section are:
- Use a problem solving strategy for word problems
- Solve number word problems
- Solve percent applications
- Solve simple interest applications
2.2.1 Use a Problem Solving Strategy for Word Problems
Now that we can solve equations, we are ready to apply our new skills to word problems. We will develop a strategy we can use to solve any word problem successfully.
Normal yearly snowfall at the local ski resort is $12$ inches more than twice the amount it received last season. The normal yearly snowfall is $62$ inches. What was the snowfall last season at the ski resort?
| the problem. | |
| what you are looking for. | What was the snowfall last season? |
| what we are looking for and choose a variable to represent it. | Let $s=$ the snowfall last season. |
| Restate the problem in one sentence with all the important information. | |
| Translate into an equation. | $62=2s+12$ |
| the equation. | $62=2s+12$ |
| Subtract $12$ from each side. | $62-12=2s+12-12$ |
| Simplify. | $50=2s$ |
| Divide each side by two. | $\frac{50}{2}=\frac{2s}{2}$ |
| Simplify. | $25=s$ |
| First, is our answer reasonable? Yes, having $25$ inches of snow seems OK. The problem says the normal snowfall is twelve inches more than twice the number of last season. Twice $25$ is $50$ and $12$ more than that is $62$. | |
| the question. | The snowfall last season was $25$ inches. |
We summarize an effective strategy for problem solving.
HOW TO: Use a Problem Solving Strategy for word problems.
- Read the problem. Make sure all the words and ideas are understood.
- Identify what you are looking for.
- Name what you are looking for. Choose a variable to represent that quantity.
- Translate into an equation. It may be helpful to restate the problem in one sentence with all the important information. Then, translate the English sentence into an algebra equation.
- Solve the equation using proper algebra techniques.
- Check the answer in the problem to make sure it makes sense.
- Answer the question with a complete sentence.
2.2.2 Solve Number Word Problems
We will now apply the problem solving strategy to “number word problems.” Number word problems give some clues about one or more numbers and we use these clues to write an equation. Number word problems provide good practice for using the Problem Solving Strategy.
The sum of seven times a number and eight is thirty-six. Find the number.
| the problem. | |
| what you are looking for. | the number |
| what you are looking for and choose a variable to represent it. | Let $n=$ the number. |
| Restate the problem as one sentence. Translate into an equation. | |
| the equation. Subtract eight from each side and simplify. Divide each side by seven and simplify. | $7n+8=36$ $7n=28$ $n=4$ |
| Is the sum of seven times four plus eight equal to $36$? $\begin{align*} 7 \cdot 4 +8&=36 \\ 28+8&=36 \\ 36&=36 \end{align*}$ | |
| the question. | The number is 4. |
Did you notice that we left out some of the steps as we solved this equation? If you’re not yet ready to leave out these steps, write down as many as you need.
Some number word problems ask us to find two or more numbers. It may be tempting to name them all with different variables, but so far, we have only solved equations with one variable. In order to avoid using more than one variable, we will define the numbers in terms of the same variable. Be sure to read the problem carefully to discover how all the numbers relate to each other.
The sum of two numbers is negative fifteen. One number is nine less than the other. Find the numbers.
| the problem. | |
| what you are looking for. | two numbers |
| what you are looking for by choosing a variable to represent the first number. “One number is nine less than the other.” | Let $n=$ first number. $n-9=$ second number. |
| Write as one sentence. Translate into an equation. | The sum of two numbers is negative fifteen. |
| the equation. Combine like terms. Add nine to each side and simplify. Simplify. | $n+n-9=-15$ $2n-9=15$ $2n=-6$ $n=-3$ first number $n-9$ second number $-3-9$ $-12$ |
| Is $-12$ nine less than $-3$? $\begin{align*} -3-9&=-12 \\ -12&=-12 \end{align*}$ Is their sum $-15$? $\begin{align*} -3+(-12)&=-15 \\ -15&=-15 \end{align*}$ | |
| the question. | The numbers are $-3$ and $-12$. |
Some number problems involve consecutive integers . Consecutive integers are integers that immediately follow each other. Examples of consecutive integers are:
| $1,\ 2, \ 3, \ 4$ | ||
| $-10,\ -9, \ -8, \ -7$ | ||
| $150,\ 151, \ 152, \ 153$ |
Notice that each number is one more than the number preceding it. Therefore, if we define the first integer as $n$, the next consecutive integer is $n+1$. The one after that is one more than $n+1$, so it is $n+1+1$, which is $n+2$.
| $n$ | $1^{st}$ integer |
| $n+1$ | $2^{nd}$ consecutive integer |
| $n+2$ | $3^{rd}$ consecutive integer etc. |
We will use this notation to represent consecutive integers in the next example.
Find three consecutive integers whose sum is $-54$.
| the problem. | |
| what you are looking for. | three consecutive integers |
| each of the three numbers | Let $n=1^{st}$ integer. $n+1=2^{nd}$ consecutive integer. $n+2=3^{rd}$ consecutive integer. |
| Restate as one sentence. Translate into an equation. | The sum of the three integers is $-54$. $n+n+1+n+2=-54$ |
| the equation. Combine like terms. Subtract three from each side. Divide each side by three. | $\begin{align*} n+n+1+n+2&=-54 \\ 3n+3&=-54 \\ 3n&=-57 \\ n&=-19 \ \ 1^{st} integer \\ n&+1 \ \ \ 2^{nd} integer \\ -19&+1 \\ -&18 \\ n&+2 \ \ \ 3^{rd} integer \\ -19&+2 \\-&17\\ \end{align*}$ |
| $\begin{align*} -19+(-18)+(-17) & = -54 \\ -54&=-54 \end{align*}$ | |
| the question. | The three consecutive integers are $-17$, $-18$, and $-19$. |
Now that we have worked with consecutive integers, we will expand our work to include consecutive even integers and consecutive odd integers . Consecutive even integers are even integers that immediately follow one another. Examples of consecutive even integers are:
$24$, $26$, $28$
$-12$, $-10$, $-8$
Notice each integer is two more than the number preceding it. If we call the first one $n$, then the next one is $n+2$. The one after that would be $n+2+2$ or $n+4$.
| $n$ | $1^{st}$ even integer |
| $n+2$ | $2^{nd}$ consecutive even integer |
| $n+4$ | $3^{rd}$ consecutive even integer etc. |
Consecutive odd integers are odd integers that immediately follow one another. Consider the consecutive odd integers $63$, $65$, and $67$.
$63$, $65$, $67$
$n$, $n+2$, $n+4$
| $n$ | $1^{st}$ odd integer |
| $n+2$ | $2^{nd}$ consecutive odd integer |
| $n+4$ | $3^{rd}$ consecutive odd integer etc. |
Does it seem strange to have to add two (an even number) to get the next odd number? Do we get an odd number or an even number when we add $2$ to $3$? to $11$? to $47$?
Whether the problem asks for consecutive even numbers or odd numbers, you do not have to do anything different. The pattern is still the same—to get to the next odd or the next even integer, add two.
Find three consecutive even integers whose sum is $120$.
| the problem. | |
| what you are looking for. | three consecutive even numbers |
| Let $n=1^{st}$ even integer. $n+2=2^{nd}$ consecutive even integer $n+4=3^{rd}$ consecutive even integer | |
| Restate as one sentence. Translate into an equation. | The sum of three even integers is $120$. $n+n+2+n+4=120$ |
| the equation. Combine like terms. Subtract $6$ from each side. Divide each side by $3$. | $\begin{align*} n+n+2+n+4&=120 \\ 3n+6&=120 \\ 3n&=114 \\ n&=38 \ \ \ 1^{st} \ integer \\ \\ n&+2 \ \ 2^{nd} \ integer \\ 38&+2 \\ &40 \\ \\ n&+4 \ \ 3^{rd} \ integer \\ 38&+4 \\ &42 \\ \end{align*}$ |
| $\begin{align*} 38+40+42&=120 \\ 120&=120 \end{align*}$ | |
| the question. | The three consecutive even integers are $38$, $40$, and $42$. |
When a number problem is in a real life context, we still use the same strategies that we used for the previous examples.
A couple together earns $ \$110,000$ a year. The wife earns $ \$ 16,000$ less than twice what her husband earns. What does the husband earn?
| the problem. | |
| what you are looking for. | How much does the husband earn? |
| Choose a variable to represent the amount the husband earns. The wife earns $ \$16,000$ less than twice that. | Let $h=$ the amount the husband earns. |
| Restate the problem in one sentence with all the important information. Translate into an equation. | $2h-16,000 =$ the amount the wife earns. Together the husband and wife earn $ \$110,000$. |
| the equation. Combine like terms. Add $16,000$ to both sides and simplify. Divide each side by three. | $\begin{align*} h+2h-16,000&=110,000 \\ 3h-16,000&=110,000 \\ 3h&=126,000 \\ h&=42,000 \end{align*}$ |
| $ \$ 42,000$ amount husband earns | |
| If the wife earns $ \$68,000$ and the husband earns $ \$42,000$, is that $ \$110,000$? Yes! | $2h-16,000$ amount wife earns $2(42,000)-16,000$ $84,000-16,000$ $68,000$ |
| the question. | The husband earns $ \$42,000$ a year. |
2.2.3 Solve Percent Applications
There are several methods to solve percent equations. In algebra, it is easiest if we just translate English sentences into algebraic equations and then solve the equations. Be sure to change the given percent to a decimal before you use it in the equation.
Translate and solve:
- What number is $45\%$ of $84$?
- $8.5\%$ of what amount is $ \$4.76$?
- $168$ is what percent of $112$?
| Translate into algebra. Let $n=$ the number. | $n = 0.45 \cdot 84$ |
| Multiply. | $n=37.8$ |
| $37.8$ is $45\%$ of $84$. |
| Translate. Let $n=$ the amount. | $0.085 \cdot n = \$ 4.76$ |
| Multiply. | $0.085n=4.76$ |
| Divide both sides by $0.085$ and simplify. | $n=56$ |
| $8.5\%$ of $ \$56$ is $ \$4.76$ |
| We are asked to find percent, so we must have our result in percent form. | |
| Translate into algebra. Let $p=$ the percent. | $168 = p \cdot 112$ |
| Multiply. | $168=112p$ |
| Divide both sides by $112$ and simplify. | $1.5=p$ |
| Convert to percent. | $150\%=p$ |
| $168$ is $150\%$ of $112$ |
Now that we have a problem solving strategy to refer to, and have practiced solving basic percent equations, we are ready to solve percent applications. Be sure to ask yourself if your final answer makes sense—since many of the applications we will solve involve everyday situations, you can rely on your own experience.
The label on Audrey’s yogurt said that one serving provided $12$ grams of protein, which is $24\%$ of the recommended daily amount. What is the total recommended daily amount of protein?
| What are you asked to find? | What total amount of protein is recommended? |
| Choose a variable to represent it. | Let $a=$ total amount of protein. |
| Write a sentence that gives the information to find it. | |
| Translate into an equation. | $12=0.24 \cdot a$ |
| Solve. | $50=a$ |
| Check: Does this make sense? Yes, $24\%$ is about $\frac{1}{4}$ of the total and $12$ is about $\frac{1}{4}$ of $50$. | |
| Write a complete sentence to answer the question. | The amount of protein that is recommended is $50$ g. |
Remember to put the answer in the form requested. In the next example we are looking for the percent.
Veronica is planning to make muffins from a mix. The package says each muffin will be $240$ calories and $60$ calories will be from fat. What percent of the total calories is from fat?
| What are you asked to find? | What percent of the total calories is fat? |
| Choose a variable to represent it. | Let $p=$ percent of fat. |
| Write a sentence that gives the information to find it. | |
| Translate the sentence into an equation. | $p \cdot 240 = 60$ |
| Multiply. | $240p=60$ |
| Divide both sides by $240$. | $p=0.25$ |
| Put in percent form. | $p=25\%$ |
| Check: Does this make sense? Yes, $25\%$ is one-fourth; $60$ is one-fourth of $240$. So, $25\%$ makes sense. | |
| Write a complete sentence to answer the question. | Of the calories in each muffin, $25\%$ is fat. |
It is often important in many fields—business, sciences, pop culture—to talk about how much an amount has increased or decreased over a certain period of time. This increase or decrease is generally expressed as a percent and called the percent change .
To find the percent change, first we find the amount of change, by finding the difference of the new amount and the original amount. Then we find what percent the amount of change is of the original amount.
HOW TO: Find percent change.
- Find the amount of change. change = new amount−original amount
- Find what percent the amount of change is of the original amount. change is what percent of the original amount?
Recently, the California governor proposed raising community college fees from $ \$36$ a unit to $ \$46$ a unit. Find the percent change. (Round to the nearest tenth of a percent.)
| Find the amount of change. | $46-36=10$ |
| Find the percent. | Change is what percent of the original amount? |
| Let $p=$ the percent. | |
| Translate to an equation. | $10=p \cdot 36$ |
| Simplify. | $10=36p$ |
| Divide both sides by $36$. | $0.278=p$ |
| Change to percent form; round to the nearest tenth | $27.8\%=p$ |
| Write a complete sentence to answer the question. | The new fees are approximately a $27.8\%$ increase over the old fees. |
| Remember to round the division to the nearest thousandth in order to round the percent to the nearest tenth. |
Applications of discount and mark-up are very common in retail settings.
When you buy an item on sale, the original price has been discounted by some dollar amount. The discount rate , usually given as a percent, is used to determine the amount of the discount. To determine the amount of discount , we multiply the discount rate by the original price.
The price a retailer pays for an item is called the original cost . The retailer then adds a mark-up to the original cost to get the list price , the price he sells the item for. The mark-up is usually calculated as a percent of the original cost. To determine the amount of mark-up, multiply the mark-up rate by the original cost.
amount of discount$=$discount rate $\cdot$ original price
sale price$=$original amount$–$discount price
The sale price should always be less than the original price.
amount of mark-up$=$mark-up rate $\cdot$ original price
list price$=$original amount$+$mark-up
The list price should always be more than the original cost.
Liam’s art gallery bought a painting at an original cost of $ \$750$. Liam marked the price up $40\%$. Find:
- the amount of mark-up
- the list price of the painting
| Identify what you are asked to find, and choose a variable to represent it. | What is the amount of mark-up? Let $m=$ the amount of mark-up. |
| Write a sentence that gives the information to find it. | |
| Translate into an equation. | $m=0.40 \times 750$ |
| Solve the equation. | $m=300$ |
| Write a complete sentence. | The mark-up on the painting was $ \$300$. |
| Identify what you are asked to find, and choose a variable to represent it. | What is the list price? Let $p=$ the list price. |
| Write a sentence that gives the information to find it. | |
| Translate into an equation. | $p=750+300$ |
| Solve the equation. | $p=1,050$ |
| Check. | Is the list price more than the original cost? Is $ \$1,050$ more than $ \$750$? Yes. |
| Write a complete sentence. | The mark-up on the painting was $ \$300$. |
2.2.4 Solve Simple Interest Applications
Interest is a part of our daily lives. From the interest earned on our savings to the interest we pay on a car loan or credit card debt, we all have some experience with interest in our lives.
The amount of money you initially deposit into a bank is called the principal , $P$, and the bank pays you interest , $I$. When you take out a loan, you pay interest on the amount you borrow, also called the principal.
In either case, the interest is computed as a certain percent of the principal, called the rate of interest , $r$. The rate of interest is usually expressed as a percent per year, and is calculated by using the decimal equivalent of the percent. The variable$t$, (for time) represents the number of years the money is saved or borrowed.
Interest is calculated as simple interest or compound interest. Here we will use simple interest.
SIMPLE INTEREST
If an amount of money, $P$, called the principal, is invested or borrowed for a period of t years at an annual interest rate $r$, the amount of interest, $I$, earned or paid is
| $I=Prt$ | where | $I =$ interest $P=$ principal $r=$ rate $t=$ time |
Interest earned or paid according to this formula is called simple interest .
The formula we use to calculate interest is $I=Prt$. To use the formula we substitute in the values for variables that are given, and then solve for the unknown variable. It may be helpful to organize the information in a chart.
Areli invested a principal of $\$950$ in her bank account that earned simple interest at an interest rate of $3\%$. How much interest did she earn in five years?
$t=5$ years
| Identify what you are asked to find, and choose a variable to represent it. | What is the simple interest? Let $I=$ interest. |
| Write the formula. | $I=Prt$ |
| Substitute in the given information. | $I=(950)(0.03)(5)$ |
| Simplify. | $I=142.5$ |
| Check. Is $\$142.50$ a reasonable amount of interest on $\$950$? Yes. | |
| Write a complete sentence. | The interest is $\$142.50$. |
There may be times when we know the amount of interest earned on a given principal over a certain length of time, but we do not know the rate.
Hang borrowed $\$7,500$ from her parents to pay her tuition. In five years, she paid them $\$1,500$ interest in addition to the $\$7,500$ she borrowed. What was the rate of simple interest?
$I= \$1500$
| Identify what you are asked to find, and choose a variable to represent it. | What is the rate of simple interest? Let $r=$ rate of interest. |
| Write the formula. Substitute in the given information. Multiply. Divide. Change to percent form. | $\begin{align*} I&=Prt \\ 1,500&=(7,500)r(5) \\ 1,500&=37,500r \\ 0.04&= r \\ 4\% &=r \end{align*}$ |
| Check. $\begin{align*} I&=Prt \\ 1,500&=(7,500)(0.04)(5) \\ 1,500&=1,500 \end{align*}$ | |
| Write a complete sentence. | The rate of interest was $4\%$. |
In the next example, we are asked to find the principal—the amount borrowed.
Sean’s new car loan statement said he would pay $\$4,866.25$ in interest from a simple interest rate of $8.5\%$ over five years. How much did he borrow to buy his new car?
$I=4,866.25$
| Identify what you are asked to find, and choose a variable to represent it. | What is the amount borrowed (the principal)? Let $P=$ principal borrowed. |
| Write the formula. Substitute in the given information. Multiply. Divide. | $\begin{align*} I&=Prt \\ 4,866.25&=P(0.085)(5) \\ 4,866.25&=0.425P \\ 11,450&=P \end{align*}$ |
| Check. | |
| Write a complete sentence. | The principal was $ \$11,450$. |
CC Licensed Content, Original
- Revision and Adaption. Provided by: Minute Math. License: CC BY 4.0
CC Licensed Content, Shared Previously
- Marecek, L., & Mathis, A. H. (2020). Use a Problem Solving Strategy. In Intermediate Algebra 2e. OpenStax. https://openstax.org/books/intermediate-algebra-2e/pages/2-2-use-a-problem-solving-strategy . License: CC BY 4.0 . Access for free at https://openstax.org/books/intermediate-algebra-2e/pages/2-introduction
Share this:
- No products in the cart.

The home of mathematics education in New Zealand.
- Forgot password ?
- Teaching material
- Problem solving activities
- Problem Solving Information
- Problem Solving Strategies
Problem solving strategies
Thanks for visiting NZMaths. We are preparing to close this site by the end of August 2024. Maths content is still being migrated onto Tāhūrangi, and we will be progressively making enhancements to Tāhūrangi to improve the findability and presentation of content.
For more information visit https://tahurangi.education.govt.nz/updates-to-nzmaths
What are problem solving strategies?
Strategies are things that Pólya would have us choose in his second stage of problem solving and use in his third stage ( What is Problem Solving? ). In actual fact he called them heuristics . They are a collection of general approaches that might work for a number of problems.
There are a number of common strategies that students of primary age can use to help them solve problems. We discuss below several that will be of value for problems on this website and in books on problem solving.
Common Problem Solving Strategies
- Guess (includes guess and check, guess and improve)
- Act It Out (act it out and use equipment)
- Draw (this includes drawing pictures and diagrams)
- Make a List (includes making a table)
- Think (includes using skills you know already)
We have provided a copymaster for these strategies so that you can make posters and display them in your classroom. It consists of a page per strategy with space provided to insert the name of any problem that you come across that uses that particular strategy (Act it out, Draw, Guess, Make a List). This kind of poster provides good revision for students.
An in-depth look at strategies
We now look at each of the following strategies and discuss them in some depth. You will see that each strategy we have in our list includes two or more subcategories.
- Guess and check is one of the simplest strategies. Anyone can guess an answer. If they can also check that the guess fits the conditions of the problem, then they have mastered guess and check. This is a strategy that would certainly work on the Farmyard problem described below but it could take a lot of time and a lot of computation. Because it is so simple, you may have difficulty weaning some students away from guess and check. As problems get more difficult, other strategies become more important and more effective. However, sometimes when students are completely stuck, guessing and checking will provide a useful way to start to explore a problem. Hopefully that exploration will lead to a more efficient strategy and then to a solution.
- Guess and improve is slightly more sophisticated than guess and check. The idea is that you use your first incorrect guess to make an improved next guess. You can see it in action in the Farmyard problem. In relatively straightforward problems like that, it is often fairly easy to see how to improve the last guess. In some problems though, where there are more variables, it may not be clear at first which way to change the guessing.
- Young students especially, enjoy using Act it Out . Students themselves take the role of things in the problem. In the Farmyard problem, the students might take the role of the animals though it is unlikely that you would have 87 students in your class! But if there are not enough students you might be able to include a teddy or two. This is an effective strategy for demonstration purposes in front of the whole class. On the other hand, it can also be cumbersome when used by groups, especially if a largish number of students is involved. Sometimes the students acting out the problem may get less out of the exercise than the students watching. This is because the participants are so engrossed in the mechanics of what they are doing that they don’t see the underlying mathematics.
- Use Equipment is a strategy related to Act it Out. Generally speaking, any object that can be used in some way to represent the situation the students are trying to solve, is equipment. One of the difficulties with using equipment is keeping track of the solution. The students need to be encouraged to keep track of their working as they manipulate the equipment. Some students need to be encouraged and helped to use equipment. Many students seem to prefer to draw. This may be because it gives them a better representation of the problem in hand. Since there are problems where using equipment is a better strategy than drawing, you should encourage students' use of equipment by modelling its use yourself from time to time.
- It is fairly clear that a picture has to be used in the strategy Draw a Picture . But the picture need not be too elaborate. It should only contain enough detail to help solve the problem. Hence a rough circle with two marks is quite sufficient for chickens and a blob plus four marks will do a pig. All students should be encouraged to use this strategy at some point because it helps them ‘see’ the problem and it can develop into quite a sophisticated strategy later.
- It’s hard to know where Drawing a Picture ends and Drawing a Diagram begins. You might think of a diagram as anything that you can draw which isn’t a picture. But where do you draw the line between a picture and a diagram? As you can see with the chickens and pigs, discussed above, regular picture drawing develops into drawing a diagram. Venn diagrams and tree diagrams are particular types of diagrams that we use so often they have been given names in their own right.
- There are a number of ways of using Make a Table . These range from tables of numbers to help solve problems like the Farmyard, to the sort of tables with ticks and crosses that are often used in logic problems. Tables can also be an efficient way of finding number patterns.
- When an Organised List is being used, it should be arranged in such a way that there is some natural order implicit in its construction. For example, shopping lists are generally not organised. They usually grow haphazardly as you think of each item. A little thought might make them organised. Putting all the meat together, all the vegetables together, and all the drinks together, could do this for you. Even more organisation could be forced by putting all the meat items in alphabetical order, and so on. Someone we know lists the items on her list in the order that they appear on her route through the supermarket.
- Being systematic may mean making a table or an organised list but it can also mean keeping your working in some order so that it is easy to follow when you have to go back over it. It means that you should work logically as you go along and make sure you don’t miss any steps in an argument. And it also means following an idea for a while to see where it leads, rather than jumping about all over the place chasing lots of possible ideas.
- It is very important to keep track of your work. We have seen several groups of students acting out a problem and having trouble at the end simply because they had not kept track of what they were doing. So keeping track is particularly important with Act it Out and Using Equipment. But it is important in many other situations too. Students have to know where they have been and where they are going or they will get hopelessly muddled. This begins to be more significant as the problems get more difficult and involve more and more steps.
- In many ways looking for patterns is what mathematics is all about. We want to know how things are connected and how things work and this is made easier if we can find patterns. Patterns make things easier because they tell us how a group of objects acts in the same way. Once we see a pattern we have much more control over what we are doing.
- Using symmetry helps us to reduce the difficulty level of a problem. Playing Noughts and crosses, for instance, you will have realised that there are three and not nine ways to put the first symbol down. This immediately reduces the number of possibilities for the game and makes it easier to analyse. This sort of argument comes up all the time and should be grabbed with glee when you see it.
- Finally working backwards is a standard strategy that only seems to have restricted use. However, it’s a powerful tool when it can be used. In the kind of problems we will be using in this web-site, it will be most often of value when we are looking at games. It frequently turns out to be worth looking at what happens at the end of a game and then work backward to the beginning, in order to see what moves are best.
- Then we come to use known skills . This isn't usually listed in most lists of problem solving strategies but as we have gone through the problems in this web site, we have found it to be quite common. The trick here is to see which skills that you know can be applied to the problem in hand. One example of this type is Fertiliser (Measurement, level 4). In this problem, the problem solver has to know the formula for the area of a rectangle to be able to use the data of the problem. This strategy is related to the first step of problem solving when the problem solver thinks 'have I seen a problem like this before?' Being able to relate a word problem to some previously acquired skill is not easy but it is extremely important.
Study Guides > Prealgebra
Using a problem-solving strategy to solve number problems, learning outcomes.
- Apply the general problem-solving strategy to number problems
- Identify how many numbers you are solving for given a number problem
- Solve consecutive integer problems
| Step 1. the problem. Do you understand all the words? | |
| Step 2. what you are looking for. | the number |
| Step 3. Choose a variable to represent the number. | Let [latex]n=\text{the number}[/latex] |
| Step 4. Restate as one sentence. Translate into an equation. | [latex]n-6\enspace\Rightarrow[/latex] The difference of a number and 6 [latex]=\enspace\Rightarrow[/latex] is [latex]13\enspace\Rightarrow[/latex] thirteen |
| Step 5. the equation. Add 6 to both sides. Simplify. | [latex]n-6=13[/latex] [latex-display]n-6\color{red}{+6}=13\color{red}{+6}[/latex-display] [latex]n=19[/latex] |
| Step 6. The difference of [latex]19[/latex] and [latex]6[/latex] is [latex]13[/latex]. It checks. | |
| Step 7. the question. | The number is [latex]19[/latex]. |
| Step 1. the problem. | |
| Step 2. what you are looking for. | the number |
| Step 3. Choose a variable to represent the number. | Let [latex]n=\text{the number}[/latex] |
| Step 4. Restate the problem as one sentence. Translate into an equation. | [latex]2n\enspace\Rightarrow[/latex] The sum of twice a number [latex]+\enspace\Rightarrow[/latex] and [latex]7\enspace\Rightarrow[/latex] seven [latex]=\enspace\Rightarrow[/latex] is [latex]15\enspace\Rightarrow[/latex] fifteen |
| Step 5. the equation. | [latex]2n+7=15[/latex] |
| Subtract 7 from each side and simplify. | [latex]2n=8[/latex] |
| Divide each side by 2 and simplify. | [latex]n=4[/latex] |
| Step 6. is the sum of twice [latex]4[/latex] and [latex]7[/latex] equal to [latex]15[/latex]? [latex-display]2\cdot{4}+7=15[/latex-display] [latex-display]8+7=15[/latex-display] [latex]15=15\quad\checkmark[/latex] | |
| Step 7. the question. | The number is [latex]4[/latex]. |
Solving for Two or More Numbers
| Step 1. the problem. | ||
| Step 2. what you are looking for. | You are looking for two numbers. | |
| Step 3. Choose a variable to represent the first number. What do you know about the second number? Translate. | Let [latex]n=\text{1st number}[/latex] One number is five more than another. [latex]x+5={2}^{\text{nd}}\text{number}[/latex] | |
| Step 4. Restate the problem as one sentence with all the important information. Translate into an equation. Substitute the variable expressions. | The sum of the numbers is [latex]21[/latex]. The sum of the 1st number and the 2nd number is [latex]21[/latex]. [latex]n\enspace\Rightarrow[/latex] First number [latex]+\enspace\Rightarrow[/latex] + [latex]n+5\enspace\Rightarrow[/latex] Second number [latex]=\enspace\Rightarrow[/latex] = [latex]21\enspace\Rightarrow[/latex] 21 | |
| Step 5. the equation. | [latex]n+n+5=21[/latex] | |
| Combine like terms. | [latex]2n+5=21[/latex] | |
| Subtract five from both sides and simplify. | [latex]2n=16[/latex] | |
| Divide by two and simplify. | [latex]n=8[/latex] 1st number | |
| Find the second number too. | [latex]n+5[/latex] 2nd number | |
| Substitute [latex]n = 8[/latex] | [latex]\color{red}{8}+5[/latex] | |
| [latex]13[/latex] | ||
| Step 6. | ||
| Do these numbers check in the problem? Is one number 5 more than the other? Is thirteen, 5 more than 8? Yes. Is the sum of the two numbers 21? | [latex]13\stackrel{\text{?}}{=}8+5[/latex] [latex-display]13=13\quad\checkmark[/latex-display] [latex-display]8+13\stackrel{\text{?}}{=}21[/latex-display] [latex]21=21\quad\checkmark[/latex] | |
| Step 7. the question. | The numbers are [latex]8[/latex] and [latex]13[/latex]. |
| Step 1. the problem. | ||
| Step 2. what you are looking for. | two numbers | |
| Step 3. Choose a variable. What do you know about the second number? Translate. | Let [latex]n=\text{1st number}[/latex] One number is [latex]4[/latex] less than the other. [latex]n-4={2}^{\text{nd}}\text{number}[/latex] | |
| Step 4. Write as one sentence. Translate into an equation. Substitute the variable expressions. | The sum of two numbers is negative fourteen. [latex]n\enspace\Rightarrow[/latex] First number [latex]+\enspace\Rightarrow[/latex] + [latex]n-4\enspace\Rightarrow[/latex] Second number [latex]=\enspace\Rightarrow[/latex] = [latex]-14\enspace\Rightarrow[/latex] -14 | |
| Step 5. the equation. | [latex]n+n-4=-14[/latex] | |
| Combine like terms. | [latex]2n-4=-14[/latex] | |
| Add 4 to each side and simplify. | [latex]2n=-10[/latex] | |
| Divide by 2. | [latex]n=-5[/latex] 1st number | |
| Substitute [latex]n=-5[/latex] to find the 2 number. | [latex]n-4[/latex] 2nd number | |
| [latex]\color{red}{-5}-4[/latex] | ||
| [latex]-9[/latex] | ||
| Step 6. | ||
| Is −9 four less than −5? Is their sum −14? | [latex]-5-4\stackrel{\text{?}}{=}-9[/latex] [latex-display]-9=-9\quad\checkmark[/latex-display] [latex-display]-5+(-9)\stackrel{\text{?}}{=}-14[/latex-display] [latex]-14=-14\quad\checkmark[/latex] | |
| Step 7. the question. | The numbers are [latex]−5[/latex] and [latex]−9[/latex]. |
| Step 1. the problem. | ||
| Step 2. what you are looking for. | two numbers | |
| Step 3. Choose a variable. One number is ten more than twice another. | Let [latex]x=\text{1st number}[/latex] [latex]2x+10={2}^{\text{nd}}\text{number}[/latex] | |
| Step 4. Restate as one sentence. | Their sum is one. | |
| Translate into an equation | [latex]x+(2x+10)\enspace\Rightarrow[/latex] The sum of the two numbers [latex]=\enspace\Rightarrow[/latex] is [latex]1\enspace\Rightarrow[/latex] 1 | |
| Step 5. the equation. | [latex]x+2x+10=1[/latex] | |
| Combine like terms. | [latex]3x+10=1[/latex] | |
| Subtract 10 from each side. | [latex]3x=-9[/latex] | |
| Divide each side by 3 to get the first number. | [latex]x=-3[/latex] | |
| Substitute to get the second number. | [latex]2x+10[/latex] | |
| [latex]2(\color{red}{-3})+10[/latex] | ||
| [latex]4[/latex] | ||
| Step 6. | ||
| Is 4 ten more than twice −3? Is their sum 1? | [latex]2(-3)+10\stackrel{\text{?}}{=}4[/latex] [latex-display]-6+10=4[/latex-display] [latex-display]4=4\quad\checkmark[/latex-display] [latex-display]-3+4\stackrel{\text{?}}{=}1[/latex-display] [latex]1=1\quad\checkmark[/latex] | |
| Step 7. the question. | The numbers are [latex]−3[/latex] and [latex]4[/latex]. |
Solving for Consecutive Integers
| Step 1. the problem. | ||
| Step 2. what you are looking for. | two consecutive integers | |
| Step 3. | Let [latex]n=\text{1st integer}[/latex] [latex]n+1=\text{next consecutive integer}[/latex] | |
| Step 4. Restate as one sentence. Translate into an equation. | [latex]n+n+1\enspace\Rightarrow[/latex] The sum of the integers [latex]=\enspace\Rightarrow[/latex] is [latex]47\enspace\Rightarrow[/latex] 47 | |
| Step 5. the equation. | [latex]n+n+1=47[/latex] | |
| Combine like terms. | [latex]2n+1=47[/latex] | |
| Subtract 1 from each side. | [latex]2n=46[/latex] | |
| Divide each side by 2. | [latex]n=23[/latex] 1st integer | |
| Substitute to get the second number. | [latex]n+1[/latex] 2nd integer | |
| [latex]\color{red}{23}+1[/latex] | ||
| [latex]24[/latex] | ||
| Step 6. | [latex]23+24\stackrel{\text{?}}{=}47[/latex] [latex]47=47\quad\checkmark[/latex] | |
| Step 7. the question. | The two consecutive integers are [latex]23[/latex] and [latex]24[/latex]. |
| Step 1. the problem. | ||
| Step 2. what you are looking for. | three consecutive integers | |
| Step 3. | Let [latex]n=\text{1st integer}[/latex] [latex-display]n+1=\text{2nd consecutive integer}[/latex-display] [latex-display]n+2=\text{3rd consecutive integer}[/latex-display] | |
| Step 4. Restate as one sentence. Translate into an equation. | [latex]n\enspace +\enspace n+1\enspace +\enspace n+2\enspace\Rightarrow[/latex] The sum of the three integers [latex]=\enspace\Rightarrow[/latex] is [latex]42\enspace\Rightarrow[/latex] 42 | |
| Step 5. the equation. | [latex]n+n+1+n+2=42[/latex] | |
| Combine like terms. | [latex]3n+3=42[/latex] | |
| Subtract 3 from each side. | [latex]3n=39[/latex] | |
| Divide each side by 3. | [latex]n=13[/latex] 1st integer | |
| Substitute to get the second number. | [latex]n+1[/latex] 2nd integer | |
| [latex]\color{red}{13}+1[/latex] | ||
| [latex]24[/latex] | ||
| Substitute to get the third number. | [latex]n+2[/latex] 3rd integer | |
| [latex]\color{red}{13}+2[/latex] | ||
| [latex]15[/latex] | ||
| Step 6. | [latex]13+14+15\stackrel{\text{?}}{=}42[/latex] [latex]42=42\quad\checkmark[/latex] | |
| Step 7. the question. | The three consecutive integers are [latex]13[/latex], [latex]14[/latex], and [latex]15[/latex]. |
Licenses & Attributions
Cc licensed content, shared previously.
- Ex: Linear Equation Application with One Variable - Number Problem. Authored by: James Sousa (Mathispower4u.com). License: CC BY: Attribution .
- Ex: Write and Solve an Equation for Consecutive Natural Numbers with a Given Sum. Authored by: James Sousa (Mathispower4u.com). License: CC BY: Attribution .
- Write and Solve a Linear Equations to Solve a Number Problem (1) Mathispower4u . Authored by: James Sousa (Mathispower4u.com) for Lumen Learning. License: CC BY: Attribution .
- Question ID 142763, 142770, 142775, 142806, 142811, 142816, 142817. Authored by: Lumen Learning. License: CC BY: Attribution . License terms: IMathAS Community License, CC-BY + GPL.
CC licensed content, Specific attribution
- Prealgebra. Provided by: OpenStax License: CC BY: Attribution . License terms: Download for free at http://cnx.org/contents/ [email protected] .
We want your feedback
Please add a message.
Message received. Thanks for the feedback.

Michigan S.
Problem Solving Strategy: Use simpler numbers
It takes Leon 1/3 hour to ride his bicycle from his home to John's home. One day, after he arrived at John's home, Leon realized he had forgotten to bring a book. So he returned home to get the book and then rode back to John's. After visiting, he rode home again. How many hours did Leon ride in all?
1 Expert Answer

Patrick B. answered • 08/16/19
Math and computer tutor/teacher
1/3 <--- going to John's; he forgot the book
1/3 <--- return home to get the book
1/3 <--- rode back to John's
1/3 <--- went home
4/3 altogether. BUT...
1 hour = 60 minutes
4/3 hours = 1 hour + 1/3 hour = 1 hour and 20 minutes;
Still looking for help? Get the right answer, fast.
Get a free answer to a quick problem. Most questions answered within 4 hours.
Choose an expert and meet online. No packages or subscriptions, pay only for the time you need.
RELATED TOPICS
Related questions, what are all the common multiples of 12 and 15.
Answers · 9
need to know how to do this problem
Answers · 8
what are methods used to measure ingredients and their units of measure
How do you multiply money.
Answers · 6
spimlify 4x-(2-3x)-5
Answers · 14
RECOMMENDED TUTORS

Stephanie S.

find an online tutor
- Math tutors
- Algebra tutors
- College Math tutors
- 7th Grade Math tutors
- ACCUPLACER College-Level Math tutors
- Advanced College Math tutors
- SAT Math tutors
- ACT Math tutors
related lessons
- Elementary Math Help
- SAT Math Test Format and Strategies
- ACT Math Test Format and Strategies
- Prealgebra Math Help
- Math Resources and Math Lessons
- GRE Quant Test Format and Strategies
- ACT Reading Test Format and Strategies

IMAGES
COMMENTS
Problem Solving Strategy 4 (Make Up Numbers). (Squares on a Chess Board) Think / Pair / Share; Problem Solving Strategy 5 (Try a Simpler Problem). Problem Solving Strategy 6 (Work Systematically). Problem Solving Strategy 7 (Use Manipulatives to Help You Investigate). Problem Solving Strategy 8 (Look for and Explain Patterns). Think / Pair / Share
Step 1: Understanding the problem. We are given in the problem that there are 25 chickens and cows. All together there are 76 feet. Chickens have 2 feet and cows have 4 feet. We are trying to determine how many cows and how many chickens Mr. Jones has on his farm. Step 2: Devise a plan.
A Problem Solving Strategy: Find the Math, Remove the Context. Sometimes the problem has a lot of details in it that are unimportant, or at least unimportant for getting started. The goal is to find the underlying math problem, then come back to the original question and see if you can solve it using the math.
Here are five strategies to help students check their solutions. 1. Use the Inverse Operation. For simpler problems, a quick and easy problem solving strategy is to use the inverse operation. For example, if the operation to solve a word problem is 56 ÷ 8 = 7 students can check the answer is correct by multiplying 8 × 7.
Step 4: Check the Solution. After working through the plan and coming up with a solution, it is important to see first of all if the solution makes sense. Then, if it seems to be reasonable, check to be sure that it is accurate. In other words, do a quick estimate first, and then check to be sure the answer is exact.
This is a problem-solving strategy that can be used with difficult concepts such as manipulating ratios or fractions. If a problem is confusing, the numbers can be rounded, or simpler numbers can be used to help make a plan to solve it. ... First, have students solve the problem using the simpler numbers. I left the house 1:00, traveled 12 ...
Problem Solving Strategy 6 (Work Systematically). If you are working on simpler problems, it is useful to keep track of what you have figured out and what changes as the problem gets more complicated. For example, in this problem you might keep track of how many 1 × 1 squares are on each board, how many 2 × 2 squares on are each board, how ...
Please, "make it simpler"! That strategy is an especially good choice from the list of problem solving-strategies. Let's look at a simpler, but similar, problem. It's simpler because the numbers are smaller, and you could even draw a picture to prove it's correct. If 3 Glinks equal a Glonk. And 2 Glonks equal a Glooie.
25516-425881148-1.pdf. MATH 111. 1. Problem Solving. "Solving a problem for which you know there's an answer is like climbing a mountain with a guide, along a trail someone else has laid. In mathematics, the truth is somewhere out there in a place no one knows, beyond all the beaten paths.". - Yoko Ogawa.
In this video, we explore one of eight problem-solving strategies for the primary math student. Students are introduced to the Make it Simpler strategy and t...
5. Find a pattern. Finding a pattern is a strategy in which students look for patterns in the given information in order to solve the problem. When the problem consists of data like numbers or events that are repeated then it can be solved using the "find a pattern" problem-solving strategy.
Apply the general problem-solving strategy to number problems; Identify how many numbers you are solving for given a number problem; Solve consecutive integer problems; Now we will translate and solve number problems. In number problems, you are given some clues about one or more numbers, and you use these clues to build an equation.
How To Use a Problem Solving Strategy for Word Problems. Read the problem. Make sure all the words and ideas are understood. Identify what you are looking for. Name what you are looking for. Choose a variable to represent that quantity. Translate into an equation. It may be helpful to restate the problem in one sentence with all the important ...
We then carry on with the same logic through the numbers from 11 to 20 to find out what our "smallest possible number" must be multiplied by in order to have these as factors, as shown below. 11. Need to multiply by it, it is prime. 16. We already have 8 (i.e. 2 x 2 x 2 above), but need an extra 2. 12.
Solve simple interest applications; Be Prepared 2.2. Before you get started, take this readiness quiz. ... Use a Problem Solving Strategy for Word Problems. ... We will now apply the problem solving strategy to "number word problems." Number word problems give some clues about one or more numbers and we use these clues to write an equation.
Solving Number Problems Now we will translate and solve number problems. In number problems, you are given some clues about one or more numbers, and you use these clues to build an equation. Number problems don't usually arise on an everyday basis, but they provide a good introduction to practicing the Problem-Solving Strategy.
2.2 Use a Solving Problem Strategy. Topics covered in this section are: Use a problem solving strategy for word problems; Solve number word problems; Solve percent applications; Solve simple interest applications; 2.2.1 Use a Problem Solving Strategy for Word Problems. Now that we can solve equations, we are ready to apply our new skills to ...
If an amount of money, P, called the principal, is invested or borrowed for a period of t years at an annual interest rate r, the amount of interest, I, earned or paid is: I = interest I = Prt where P = principal r = rate t = time. 2.3: Use a Problem Solving Strategy CC BY 4.0 OpenStax source content. Now that we can solve equations, we are ...
In number problems, you are given some clues about one or more numbers, and you use these clues to build an equation. Number problems don't usually arise on an everyday basis, but they provide a good introduction to practicing the Problem-Solving Strategy. Remember to look for clue words such as difference, of, and and. Find the number. Step 1.
What are problem solving strategies? ... So guess and improve is a method of solution that you can use on a number of problems. Some strategies can give you an idea of how you might tackle a problem. ... Guess: Moving from guess and check to guess and improve, is an obvious development of a simple strategy. Guess and check may work well in some ...
Apply the general problem-solving strategy to number problems. Identify how many numbers you are solving for given a number problem. Solve consecutive integer problems. Now we will translate and solve number problems. In number problems, you are given some clues about one or more numbers, and you use these clues to build an equation.
Step 3. Name what we are looking for. Choose a variable to represent that quantity. We can use any letter for the variable, but choose one that makes it easy to remember what it represents. Step 4. Translate into an equation. It may be helpful to restate the problem in one sentence with all the important information.
Problem Solving Strategy: Use simpler numbers. It takes Leon 1/3 hour to ride his bicycle from his home to John's home. One day, after he arrived at John's home, Leon realized he had forgotten to bring a book. So he returned home to get the book and then rode back to John's. After visiting, he rode home again.