assignment 6 writing a function rule

You can excel with Caddell!

Give us a call (917) 722-0677

Writing a Function Rule

This lesson is how to write a function rule. This video shows how functions typically behave, and how to write them down. Functions usually have a variable with a coefficient in front that represents the rate of change and has a constant value that represents the starting point of the function. After you finish this lesson, view all of our Algebra 1 lessons and practice problems.

The setup for this would look like:

Examples of Writing a Function Rule

Video-Lesson Transcript

We’re going to cover how to write a function rule for particularly linear functions .

Linear function has a basic form:

For example:

So we’ll have

Let’s look at another example.

The money will be equal to starting amount plus the amount you add to it times the number of weeks that passed.

Online Test Prep for Schools

Terms of Service

Privacy Policy

TACHS Vocabulary  

Past Regents Exams

As seen on:

Graphing a Function Rule

In introductory units on functions, algebra 1 students become proficient in graphing a function rule representing a function and learn how to distinguish between discrete and continuous functions.

Although some students may experience this topic as challenging, math teachers can help out by applying diverse teaching strategies. In this article, we share a few such strategies. Use them in your class and see your students’ knowledge soar in no time!

How to Teach Graphing a Function Rule

What is a function rule.

For starters, explain what a function rule is. You can define it as a mathematical rule that can be used to describe the general trend of the function. A rule can be taken as an equation representing any relationship. A function rule can be used to interpret the function as a graph.

You can also include this video that contains a simple explanation of the difference between an equation and a function, as well as the overlapping areas between the two. In addition, you can also play this video that explains how to obtain a function from an equation.

How to Graph a Function Rule

Point out to students that when we’re given a function rule, we can make a table of values satisfying the function rule and graph these points to discover the shape of the function. Add that now we will cover two types of function graphs:

• linear function graphs
• nonlinear function graphs

Students have already learned in previous lessons what linear and nonlinear functions are, but it’s always good to review this. Remind students that a function is linear if its graph makes a straight line, whereas the graphs of nonlinear functions aren’t straight lines (ex: parabola).

Tell students that you will demonstrate how to graph the following function rule: y = 2x + 1. As mentioned earlier, we’ll begin with a table of values that will satisfy the given function rule. Then we’ll graph each of the points from the table.

More specifically, we’ll select x-values and plug them into the function rule. By doing this, we’ll be able to get the y-values. Once you plug those values into the equation, you will get a y-value. These x-values and y-values represent the coordinates for a single point. Then, we’ll connect the dots.

For instance, you can use the following table:

So if x = – 2, by plugging this value into y = 2x + 1, we’ll obtain the following:

y = 2 (- 2) + 1

y = – 4 + 1

y = – 3

This means that the ordered pair (x, y) will be (- 2, – 3). By applying the same process with the other x-values, we obtain these ordered pairs (- 2, – 3), ( -1, 0), (0, 1), (1, 3), (2, 5). Now the only thing left to do is to plot each of these points on the graph. Thus, we produce the following:

Point out that this graph represents the graph of the function rule y = 2x + 1. Ask students to analyze the graph and reflect – does this graph represent a nonlinear graph or a linear one? How do they know?

Discrete and Continuous Graphs

Once students are comfortable with graphing any function rule, you can proceed with explaining what the difference between discrete and continuous graphs is. Explain that a discrete graph is composed of distinct isolated points on the graph. Present an example on the whiteboard:

Then, explain that a continuous graph, on the other hand, is a graph that is unbroken and data exists between plotted values. Draw a continuous graph on the whiteboard and demonstrate this to students:

Use this video in your classroom to illustrate a real-life example of discrete and continuous graphs. The video contains an example of a local cheese maker who’s making cheddar cheese to sell at a farmer’s market.

The video shows the amount of milk used to make the cheese and the price at which the cheese is sold. By first writing a function and graphing it, students can learn to identify whether the graph is discrete or continuous.

Activities to Practice Graphing a Function Rule

This activity will help students improve their skills at graphing a function rule. To implement this activity in your classroom, the only thing you’ll need is this Assignment Worksheet (Members Only). Print out enough copies for all students (one per student).

The worksheet contains exercises where students are asked to make a table of values of each given function and then graph each function rule using this table of values, as well as determine whether the function is continuous or discrete.

Pair students up and hand out the copies. Explain that pairs work together to solve the math exercises in the worksheet. After each person has finished their worksheet, they go through the exercises of the student they’re paired with and provide feedback to each other.

Function Rule Machine Game

This is a game that will help students practice graphing a function rule, as well as identifying whether the function is continuous or discrete. To use this game in your class, you’ll need construction paper, scissors, and markers.

Draw ‘machines’ resembling a table on the construction paper and enter x-values in each machine. Leave the y-values field of the table empty. The machine also contains a function rule and a problem that needs to be solved and graphed so that the machine starts working.

An example of such a problem is as follows:

‘The amount of water w in a swimming pool, in liters, depends on the amount of time t the swimming pool is filled with water and is related by the function rule w = 1.5t. Graph each function rule and then tell whether the function is continuous or discrete.

Create several such machines, depending on the size of the class (there should be one machine per group). Divide students into groups of 3, 4 and hand out a machine to each student.

Explain they need to solve for y and graph the function rule so that the machine works again. Provide a few minutes for this. The group that manages to graph the function rule first, as well as correctly identify if it’s continuous or discrete, wins the game.

Before You Leave…

If you liked the teaching strategies on graphing a function rule that we outlined in this article, we have a whole lesson that is dedicated to this topic!

So if you’re looking for more math materials for children of all ages, sign up for our emails for plenty of free content! Feel free to also head over to our blog , and check out our free resources on patterns, equations, and graphs!

And if you’d like to become a member, sign up at Math Teacher Coach !

This article is based on:

Unit 4 – An Introduction to Functions

• 4-1 Using Graphs to Relate Two Quantities
• 4-2 Patterns and Linear Functions
• 4-3 Patterns and Nonlinear Functions
• 4-4 Graphing a Function Rule
• 4-5 Writing a Function Rule
• 4-6 Formalizing Relations and Functions
• 4-7 Arithmetic Sequences

Share this:

• Click to share on Facebook (Opens in new window)
• Click to share on Pinterest (Opens in new window)
• Click to share on Reddit (Opens in new window)
• Click to share on Twitter (Opens in new window)
• Click to print (Opens in new window)
• Click to share on LinkedIn (Opens in new window)
• Click to share on Pocket (Opens in new window)
• Click to share on Tumblr (Opens in new window)

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons
• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

6.1: Introduction to Functions

• Last updated
• Save as PDF
• Page ID 7067

• Ted Sundstrom
• Grand Valley State University via ScholarWorks @Grand Valley State University

Exercise \(\PageIndex{1}\)

Preview Activity 1 (Functions from Previous Courses) One of the most important concepts in modern mathematics is that of a function . In previous mathematics courses, we have often thought of a function as some sort of input-output rule that assigns exactly one output to each input. So in this context, a function can be thought of as a procedure for associating with each element of some set, called the domain of the function , exactly one element of another set, called the codomain of the function . This procedure can be considered an input-output-rule. The function takes the input, which is an element of the domain, and produces an output, which is an element of the codomain. In calculus and precalculus, the inputs and outputs were almost always real numbers. So the notationf \(f(x) = x^2 sin x\) means the following:

• \(f\) is the name of the function.
• \(f(x)\) is a real number. It is the output of the function when the input is the real number \(x\). For example, \[\begin{array} {rcl} {f(\dfrac{\pi}{2})} &= & {(\dfrac{\pi}{2})^2 sin(\dfrac{\pi}{2})} \\ {} &= & {\dfrac{\pi ^2}{4} \cdot 1} \\ {} &= & {\dfrac{\pi ^2}{4}.} \end{array}\]

For this function, it is understood that the domain of the function is the set \(\mathbb{R}\) of all real numbers. In this situation, we think of the domain as the set of all possible inputs. That is, the domain is the set of all possible real numbers \(x\) for which a real number output can be determined.

This is closely related to the equation \(f = x^2 sin x\). With this equation, we frequently think of \(x\) as the input and \(y\) as the output. In fact, we sometimes write \(y = f(x)\). The key to remember is that a function must have exactly one output for each input. When we write an equation such as

\(y = \dfrac{1}{2} x^3 - 1,\)

we can use this equation to define \(y\) as a function of \(x\). This is because when we substitute a real number for \(x\) (the input), the equation produces exactly one real number for \(y\) (the output). We can give this function a name, such as \(g\), and write

\(y = g(x) = \dfrac{1}{2} x^3 - 1.\)

However, as written, an equation such as

• \(y^2 = x + 3\)

cannot be used to define \(y\) as a function of \(x\) since there are real numbers that can be substituted for \(x\) that will produce more than one possible value of \(y\). For example, if \(x = 1\), then \(y^2 = 4\), and \(y\) could be -2 or 2.

Which of the following equations can be used to define a function with \(x \in \mathbb{R}\) as the input and \(y \in \mathbb{R}\) as the output?

• \(y = x^2 - 2\)
• \(y = \dfrac{1}{2} x^3 - 1\)
• \(y = \dfrac{1}{2} x sin x\)
• \(x^2 + y^2 = 4\)
• \(y = 2x - 1\)
• \(y =dfrac{x}{x - 1}\)

Preview Activity 2 (Some Other Types of Functions)

The domain and codomain of the functions in Preview Activity \(\PageIndex{1}\) is the set \(\mathbb{R}\) of all real numbers, or some subset of \(\mathbb{R}\). In most of these cases, the way in which the function associates elements of the domain with elements of the codomain is by a rule determined by some mathematical expression. For example, when we say that \(f\) is the function such that

\(f(x) = \dfrac{x}{x - 1},\)

then the algebraic rule that determines the output of the function \(f\) when the input is \(x\) is \(\dfrac{x}{x - 1}\). In this case, we would say that the domain of \(f\) is the set of all real numbers not equal to 1 since division by zero is not defined.

However, the concept of a function is much more general than this. The domain and codomain of a function can be any set, and the way in which a function associates elements of the domain with elements of the codomain can have many different forms. The input-output rule for a function can be a formula, a graph, a table, a random process, or a verbal description. We will explore two different examples in this preview activity.

• Let \(b\) be the function that assigns to each person his or her birthday (month and day). The domain of the function \(b\) is the set of all people and the codomain of \(b\) is the set of all days in a leap year (i.e., January 1 through December 31, including February 29). (a) Explain why \(b\) really is a function. We will call this the birthday function . (b) In 1995, Andrew Wiles became famous for publishing a proof of Fermat’s Last Theorem. (See A. D. Aczel, Fermat’s Last Theorem: Unlocking the Secret of an Ancient Mathematical Problem, Dell Publishing, New York, 1996.) Andrew Wiles’s birthday is April 11, 1953. Translate this fact into functional notation using the “birthday function” \(b\). That is, fill in the spaces for the following question marks: \[b(?) = ?.\] (c) Is the following statement true or false? Explain. For each day \(D\) of the year, there exists a person \(x\) such that \(b(x) = D\). (d) Is the following statement true or false? Explain. For any people \(x\) and \(y\), if \(x\) and \(y\) are different people, then \(b(x) \ne b(y)\).
• Let \(s\) be the function that associates with each natural number the sum of its distinct natural number divisors. This is called the sum of the divisors function . For example, the natural number divisors of 6 are 1, 2, 3, and 6, and so \[\begin{array} {rcl} {s(6)} &= & {1 + 2 + 3 + 6} \\ {} &= & {12.} \end{array}\] (a) Calculate \(s(k)\) for each natural number \(k\) from 1 through 15. (b) Does there exist a natural number \(n\) such that \(s(n) = 5\)? Justify your conclusion. (c) Is it possible to find two different natural numbers \(m\) and \(n\) such that \(s(m) = s(n)\)? Explain. (d) Use your responses in (b) and (c) to determine whether the following statements true or false. i. For each \(m \in \mathbb{N}\), there exists a natural number \(n\) such that \(s(n) = m\). ii. For all \(m, n \in \mathbb{N}\), if \(m \ne n\), then \(s(m) \ne s(n)\).

The Definition of a Function

The concept of a function is much more general than the idea of a function used in calculus or precalculus. In particular, the domain and codomain do not have to be subsets of \(\mathbb{R}\). In addition, the way in which a function associates elements of the domain with elements of the codomain can have many different forms. This input-output rule can be a formula, a graph, a table, a random process, a computer algorithm, or a verbal description. Two such examples were introduced in Preview Activity \(\PageIndex{2}\).

For the birthday function , the domain would be the set of all people and the codomain would be the set of all days in a leap year. For the sum of the divisors function , the domain is the set \(\mathbb{N}\) of natural numbers, and the codomain could also be \(\mathbb{N}\). In both of these cases, the input-output rule was a verbal description of how to assign an element of the codomain to an element of the domain.

We formally define the concept of a function as follows:

A function from a set \(A\) to a set \(B\) is a rule that associates with each element \(x\) of the set \(A\) exactly one element of the set \(B\). A function from \(A\) to \(B\) is also called a mapping from \(A\) to \(B\).

Function Notation . When we work with a function, we usually give it a name. The name is often a single letter, such as \(f\) or \(g\). If \(f\) is a function from the set \(A\) to be the set \(B\), we will write \(f: A \to B\). This is simply shorthand notation for the fact that \(f\) is a function from the set \(A\) to the set \(B\). In this case, we also say that \(f\) maps \(A\) to \(B\).

Let \(f: A \to B\). (This is read, “Let \(f\) be a function from \(A\) to \(B\).”) The set \(A\) is called the domain of the function \(f\), and we write \(A = dom(f)\). The set \(B\) is called the codomain of the function \(f\), and we write \(B = codom(f)\).

If \(a \in A\), then the element of \(B\) that is associated with \(a\) is denoted by \(f(a)\) and is called the image of a under \(f\) . If \(f(a) = b\), with \(b \in B\), then a is called a preimage of \(b\) under \(f\) .

Some Function Terminology with an Example. When we have a function \(f: A \to B\), we often write \(y = f(x)\). In this case, we consider \(x\) to be an unspecified object that can be chosen from the set \(A\), and we would say that \(x\) is the independent variable of the function \(f\) and \(y\) is the dependent variable of the function \(f\).

For a specific example, consider the function \(g: \mathbb{R} \to \mathbb{R}\), where \(g(x)\) is defined by the formula

\(g(x) = x^2 - 2.\)

Note that this is indeed a function since given any input \(x\) in the domain, \(\mathbb{R}\), there is exactly one output \(g(x)\) in the codomain, \(\mathbb{R}\). For example,

\[\begin{array} {rcl} {g(-2)} &= & {(-2)^2 - 2 = 2,} \\ {g(5)} &= & {5^2 - 2 = 23,} \\ {g(\sqrt 2)} &= & {(\sqrt 2)^2 - 2 = 0,} \\ {g(-\sqrt 2)} &= & {(-\sqrt 2)^2 - 2 = 0.} \end{array}\]

So we say that the image of -2 under \(g\) is 2, the image of 5 under \(g\) is 23, and so on.

Notice in this case that the number 0 in the codomain has two preimages, \(-\sqrt 2\) and \(\sqrt 2\). This does not violate the mathematical definition of a function since the definition only states that each input must produce one and only one output. That is, each element of the domain has exactly one image in the codomain. Nowhere does the definition stipulate that two different inputs must produce different outputs.

Finding the preimages of an element in the codomain can sometimes be difficult. In general, if \(y\) is in the codomain, to find its preimages, we need to ask, “For which values of \(x\) in the domain will we have \(y = g(x)\)?” For example, for the function g, to find the preimages of 5, we need to find all \(x\) for which \(g(x) = 5\). In this case, since \(g(x) = x^2 - 2\), we can do this by solving the equation

\(x^2 - 2 = 5.\)

The solutions of this equation are \(-\sqrt 7\) and \(\sqrt 7\). So for the function \(g\), the preimages of 5 are \(-\sqrt 7\) and \(\sqrt 7\). We often use set notation for this and say that the set of preimages of 5 for the function \(g\) is {\(-\sqrt 7\), \(\sqrt 7\)}.

Also notice that for this function, not every element in the codomain has a preimage. For example, there is no input \(x\) such that \(g(x) = -3\). This is true since for all real numbers \(x\), \(x^2 \ge 0\) and hence \(x^2 - 2 \ge -2\). This means that for all \(x\) in \(\mathbb{R}\), \(g(x) \ge -2\).

Finally, note that we introduced the function g with the sentence, “Consider the function \(g: \mathbb{R} \to \mathbb{R}\), where \(g(x)\) is defined by the formula \(g(x) = x^2 - 2\).” This is one correct way to do this, but we will frequently shorten this to, “Let \(g: \mathbb{R} \to \mathbb{R}\) be defined by \(g(x) = x^2 - 2\)”, or “Let \(g: \mathbb{R} \to \mathbb{R}\), where \(g(x) = x^2 - 2\).”

Progress Check 6.1 (Images and Preimages)

Let \(f: \mathbb{R} \to \mathbb{R}\) be defined by \(f(x) = x^2 - 5x\) for all \(x \in \mathbb{R}\). and let \(g: \mathbb{Z} \to \mathbb{Z}\) be defined by \(g(m) = m^2 - 5m\) for all \(m \in \mathbb{Z}\).

• Determine \(f(-3)\) and \(f(\sqrt 8)\).
• Determine \(g(2)\) and \(g(-2)\).
• Determine the set of all preimage of 6 for the function \(f\).
• Determine the set of all preimage of 6 for the function \(g\).
• Determine the set of all preimage of 2 for the function \(f\).
• Determine the set of all preimage of 2 for the function \(g\).

Add texts here. Do not delete this text first.

The Codomain and Range of a Function

Besides the domain and codomain, there is another important set associated with a function. The need for this was illustrated in the example of the function \(g\) on page 285. For this function, it was noticed that there are elements in the codomain that have no preimage or, equivalently, there are elements in the codomain that are not the image of any element in the domain. The set we are talking about is the subset of the codomain consisting of all images of the elements of the domain of the function, and it is called the range of the function.

Let \(f: A \to B\). The set \(\{f(x)\ |\ x \in A\}\) is called the range of the function \(f\) and is denoted by range (\(f\)). The range of \(f\) is sometimes called the image of the function \(f\) (or the image of \(A\) under \(f\) ).

The range of \(f: A \to B\) could equivalently be defined as follows:

range(\(f\))\( = \{y \in B\ |\ y = f(x) \text{ for some } x \in A\}\).

Notice that this means that range(\(f\)) \(\subseteq\) codom(\(f\)) but does not necessarily mean that range(\(f\)) \(=\) codom(\(f\)). Whether we have this set equality or not depends on the function \(f\). More about this will be explored in Section 6.3.

Progress Check 6.2 (Codomain and Range)

• Let \(b\) be the function that assigns to each person his or her birthday (month and day). (a) What is the domain of this function? (b) What is a codomain for this function? (c) In Preview Activity \(\PageIndex{2}\), we determined that the following statement is true: For each day \(D\) of the year, there exists a person \(x\) such that \(b(x) = D\). What does this tell us about the range of the function \(b\)? Explain.
• Let \(s\) be the function that associates with each natural number the sum of its distinct natural number factors. (a) What is the domain of this function? (b) What is a codomain for this function? (c) In Preview Activity \(\PageIndex{2}\), we determined that the following statement is false: For each \(m \in \mathbb{N}\), there exists a natural number \(n\) such that \(s(n) = m\). Give an example of a natural number \(m\) that shows this statement is false, and explain what this tells us about the range of the function \(s\).

The Graph of a Real Function

We will finish this section with methods to visually communicate information about two specific types of functions. The first is the familiar method of graphing functions that was a major part of some previous mathematics courses. For example, consider the function \(g: \mathbb{R} \to \mathbb{R}\) defined by \(g(x) = x^2 - 2x - 1\).

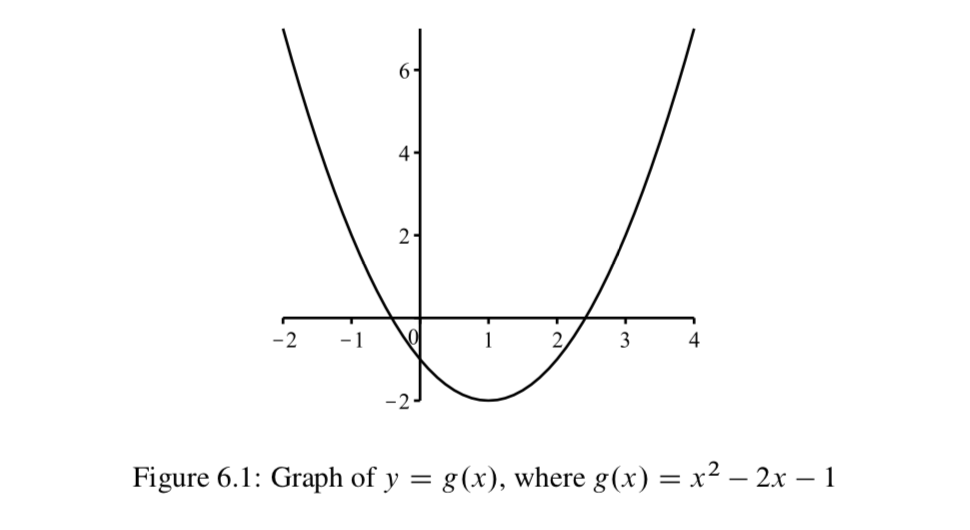
Every point on this graph corresponds to an ordered pair (\(x\), \(y\)) of real numbers, where \(y = g(x) = x^2 - 2x - 1\). Because we use the Cartesian plane when drawing this type of graph, we can only use this type of graph when both the domain and the codomain of the function are subsets of the real numbers \(\mathbb{R}\). Such a function is sometimes called a real function . The graph of a real function is a visual way to communicate information about the function. For example, the range of \(g\) is the set of all y-values that correspond to points on the graph. In this case, the graph of \(g\) is a parabola and has a vertex at the point (1, -2). ( Note : The x-coordinate of the vertex can be found by using calculus and solving the equation \(f\prime (x) = 0\).) Since the graph of the function \(g\) is a parabola, we know that pattern shown on the left end and the right end of the graph continues and we can conclude that the range of \(g\) is the set of all \(y \in \mathbb{R}\) such that \(y \ge -2\). That is,

range(\(g\))\( = \{y \in \mathbb{R}\ |\ y \ge -2\}.\)

Progress Check 6.3 (Using the Graph of a Real Function)

The graph in Figure 6.2 shows the graph of (slightly more than) two complete periods for a function \(f: \mathbb{R} \to \mathbb{R}\), where \(f(x) = Asin(Bx)\) for some positive real number constants \(A\) and \(B\).

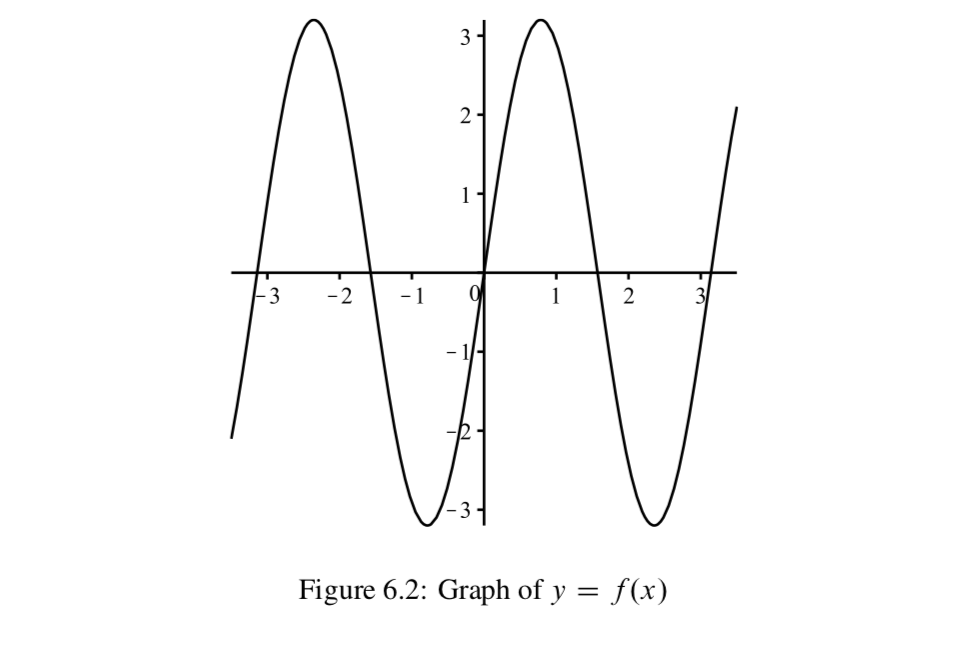
• We can use the graph to estimate the output for various inputs. This is done by estimating the \(y\)-coordinate for the point on the graph with a specified \(x\)-coordinate. On the graph, draw vertical lines at \(x = -1\) and \(x = 2\) and estimate the values of \(f(-1)\) and \(f(2)\).
• Similarly, we can estimate inputs of the function that produce a specified output. This is done by estimating the \(x\)-coordinates of the points on the graph that have a specified \(y\)-coordinate. Draw a horizontal line at \(y = 2\) and estimate at least two values of \(x\) such that \(f(x) = 2\).
• Use the graph Figure 6.2 to estimate the range of the function \(f\).

Arrow Diagrams

Sometimes the domain and codomain of a function are small, finite sets. When this is the case, we can define a function simply by specifying the outputs for each input in the domain. For example, if we let \(A = \{1, 2, 3\}\) and let \(B = \{a, b\}\), we can define a function \(F: A \to B\) by specifying that

\(F(1) = a, F(2) = a,\text{ and } F(3) = b.\)

This is a function since each element of the domain is mapped to exactly one element in \(B\). A convenient way to illustrate or visualize this type of function is with a so-called arrow diagram as shown in Figure 6.3. An arrow diagram can

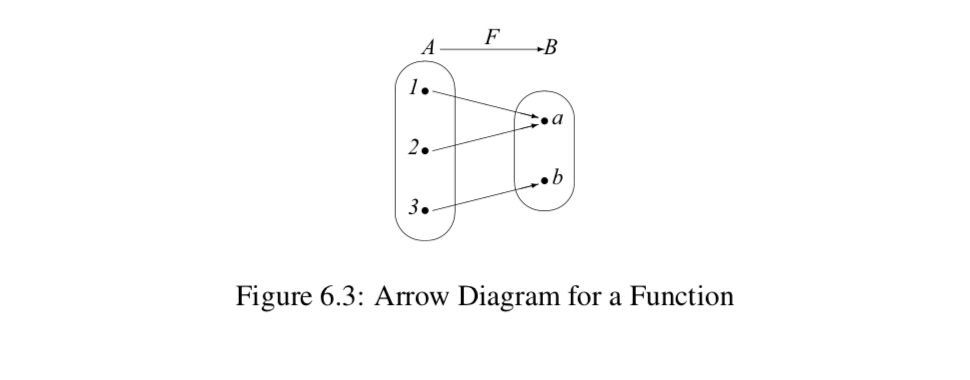
be used when the domain and codomain of the function are finite (and small). We represent the elements of each set with points and then use arrows to show how the elements of the domain are associated with elements of the codomain. For example, the arrow from the point 2 in \(A\) to the point \(a\) in \(B\) represents the fact that \(F(2) = a\). In this case, we can use the arrow diagram in Figure 6.3 to conclude that range(\(F\))\( = \{a, b\}\).

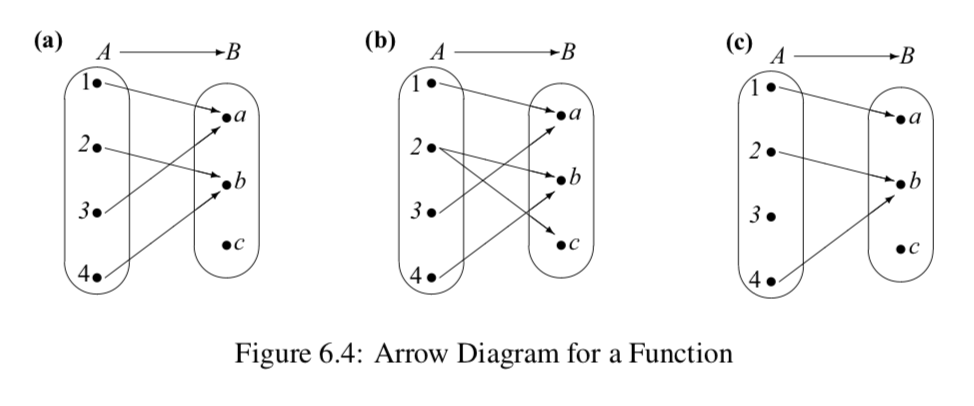
Progress Check 6.4 (Working with Arrow Diagrams)

Let \(A = \{1, 2, 3, 4\}\) and let \(B = \{a, b, c\}\).

• Which of the arrow diagrams in Figure 6.4 can be used to represent a function from \(A\) to \(B\)? Explain.

Exercises 6.1

• Let \(f: \mathbb{R} \to \mathbb{R}\) be defined by \(f(x) = x^2 - 2x\). (a) Evaluate \(f(-3)\), \(f(-1)\), \(f(1)\), and \(f(3)\). (b) Determine the set of all of the preimages of 0 and the set of all of the preimages of 4. (c) Sketch a graph of the function \(f\). (d) Determine the range of the function \(f\).
• Let \(\mathbb{R} ^{\ast} = \{x \in \mathbb{R}\ |\ x \ge 0\}\), and let \(s: \mathbb{R} \to \mathbb{R} ^{\ast}\) be defined by \(s(x) = x^2\). (a) Evaluate \(s(-3)\), \(s(-1)\), \(s(1)\), and \(s(3)\). (b) Determine the set of all of the preimages of 0 and the set of all of the preimages of 2. (c) Sketch a graph of the function \(s\). (d) Determine the range of the function \(s\).
• Let \(f: \mathbb{Z} \to \mathbb{Z}\) be defined by \(f(m) = 3 - m\). (a) Evaluate \(f(-7)\), \(f(-3)\), \(f(3)\), and \(f(7)\). (b) Determine the set of all of the preimages of 5 and the set of all of the preimages of 4. (c) Determine the range of the function \(f\). (d) This function can be considered a real function since \(\mathbb{Z} \subseteq \mathbb{R}\). Sketch a graph of this function. Note : The graph will be an infinite set of points that lie on a line. However, it will not be a line since its domain is not \(\mathbb{R}\) but is \(\mathbb{Z}\).
• Let \(f: \mathbb{Z} \to \mathbb{Z}\) be defined by \(f(m) = 2m + 1\). (a) Evaluate \(f(-7)\), \(f(-3)\), \(f(3)\), and \(f(7)\). (b) Determine the set of all of the preimages of 5 and the set of all of the preimages of 4. (c) Determine the range of the function \(f\). (d) Sketch a graph of the function \(f\). See the comments in Exercise (3d).
• Recall that a real function is a function whose domain and codomain are subsets of the real numbers R. (See page 288.) Most of the functions used in calculus are real functions. Quite often, a real function is given by a formula or a graph with no specific reference to the domain or the codomain. In these cases, the usual convention is to assume that the domain of the real function \(f\) is the set of all real numbers \(x\) for which \(f(x)\) is a real number, and that the codomain is \(\mathbb{R}\). For example, if we define the (real) function \(f\) by \[f(x) = \dfrac{x}{x - 2},\] we would be assuming that the domain is the set of all real numbers that are not equal to 2 and that the codomain in \(\mathbb{R}\). Determine the domain and range of each of the following real functions. It might help to use a graphing calculator to plot a graph of the function. (a) The function \(k\) defined by \(k(x) = \sqrt{x - 3}\) (b) The function \(F\) defined by \(F(x) = ln(2x - 1)\) (c) The function \(f\) defined by \(f(x) = 3sin(2x)\) (d) The function \(g\) defined by \(g(x) = \dfrac{4}{x^2 - 4}\) (e) The function \(G\) defined by \(G(x) = 4cos(\pi x) + 8\)
• The number of divisors function . Let \(d\) be the function that associates with each natural number the number of its natural number divisors. That is \(d: \mathbb{N} \to \mathbb{N}\) where \(d(n)\) is the number of natural number divisors of \(n\). For example, \(d(6) = 4\) since 1, 2, 3, and 6 are the natural number divisors of 6. (a) Calculate \(d(k)\) for each natural number \(k\) from 1 through 12. (b) Does there exist a natural number \(n\) such that \(d(n) = 1\)? What is the set of preimages of the natural number 1. (c) Does there exist a natural number \(n\) such that \(d(n) = 2\)? If so, determine the set of all preimages of the natural number 2. (d) Is the following statement true or false? Justify your conclusion. For all \(m, n \in \mathbb{N}\), if \(m \ne n\), then \(d(m) \ne d(n)\). (e) Calculate \(d(2^k)\) for \(k = 0\) and for each natural number \(k\) from 1 through 6. (f) Based on your work in Exercise (6e), make a conjecture for a formula for \(d(2^n)\) where \(n\) is a nonnegative integer. Then explain why your conjecture is correct. (g) Is the following statement is true or false? For each \(n \in \mathbb{N}\), there exists a natural number \(m\) such that \(d(m) = n\).
• In Exercise (6), we introduced the number of divisors function \(d\). For this function, \(d: \mathbb{N} \to \mathbb{N}\), where \(d(n)\) is the number of natural number divisors of \(n\). A function that is related to this function is the so-called set of divisors function . This can be defined as a function \(S\) that associates with each natural number the set of its distinct natural number factors. For example, \(S(6) = \{1, 2, 3, 6\}\) and \(S(10) = \{1, 2, 5, 10\}\). (a) Discuss the function \(S\) by carefully stating its domain, codomain, and its rule for determining outputs. (b) Determine \(S(n)\) for at least five different values of \(n\). (c) Determine \(S(n)\) for at least three different prime number values of \(n\). (d) Does there exist a natural number \(n\) such that card(\(S(n) = 1\))? Explain. [Recall that card(\(S(n)\)) is the number of elements in the set \(S(n)\).] (e) Does there exist a natural number \(n\) such that card(\(S(n) = 2\))? Explain. (f) Write the output for the function \(d\) in terms of the output for the function \(S\). That is, write \(d(n)\) in terms of \(S(n)\). (g) Is the following statement true or false? Justify your conclusion. For all natural numbers \(m\) and \(n\), if \(m \ne n\), then \(S(m) \ne S(n)\). (h) Is the following statement true or false? Justify your conclusion. For all sets \(T\) that are subsets of \(\mathbb{N}\), there exists a natural number \(n\) such that \(S(n) = T\). Explorations and Activities
• Creating Functions with Finite Domains. Let \(A = \{a, b, c, d\}\), \(B= \{a, b, c\}\). and \(C = \{s, t, u, v\}\). In each of the following exercises, draw an arrow diagram to represent your function when it is appropriate. (a) Create a function \(f: A \to C\) whose range is the set \(C\) or explain why it is not possible to construct such a function. (b) Create a function \(f: A \to C\) whose range is the set \(\{u,v\}\) or explain why it is not possible to construct such a function. (c) Create a function \(f: B \to C\) whose range is the set \(C\) or explain why it is not possible to construct such a function. (d) Create a function \(f: A \to C\) whose range is the set \(\{u\}\) or explain why it is not possible to construct such a function. (e) If possible, create a function \(f: A \to C\) that satisfies the following condition: For all \(x,y \in A\), if \(x \ne y\), then \(f(x) \ne f(y)\). If it is not possible to create such a function, explain why. (f) If possible, create a function \(f: A \to \{s, t, u\}\) that satisfies the following condition: For all \(x,y \in A\), if \(x \ne y\), then \(f(x) \ne f(y)\). If it is not possible to create such a function, explain why.

• Skills by Standard
• Skills by Grade
• Skills by Category

Go to profile

• Assignments
• Assessments
• Report Cards
• Our Teachers

Remove ads and gain access to the arcade and premium games!

Unlock harder levels by getting an average of 80% or higher.

Earn up to 5 stars for each level The more questions you answer correctly, the more stars you'll unlock!

Each game has 10 questions. Green box means correct. Yellow box means incorrect.

Need some help or instruction on how to do this skill?

Want a paper copy? Print a generated PDF for this skill.

Share MathGames with your students, and track their progress.

See how you scored compared to other students from around the world.

Learn Math Together.

Grade 6 - Expressions & Equations

Standard 6.EE.3.9 - Find the equation that defines the x and y data in a function table.

Included Skills:

Use variables to represent two quantities in a real-world problem that change in relationship to one another; write an equation to express one quantity, thought of as the dependent variable, in terms of the other quantity, thought of as the independent variable. Analyze the relationship between the dependent and independent variables using graphs and tables, and relate these to the equation.

If you notice any problems, please let us know .

Writing Function Rules Worksheet

Description

This assignment requires students to write a function rule from a given table. It also has a few review questions on identifying independent and dependent variables.

This worksheet is section 3.3 of Unit 3 for Math I.

Questions & Answers

Keep it integrated.

• We're hiring
• Help & FAQ
• Privacy policy
• Student privacy
• Terms of service
• Tell us what you think