unit 12 trigonometry homework 6 law of cosines

The Law of Cosines

For any triangle ...

a , b and c are sides.

C is the angle opposite side c

... the Law of Cosines (also called the Cosine Rule ) says:

c 2 = a 2 + b 2 − 2ab cos(C)

It helps us solve some triangles. Let's see how to use it.

Example: How long is side "c" ... ?

We know angle C = 37º, and sides a = 8 and b = 11

Answer: c = 6.67

How to Remember

How can you remember the formula?

Well, it helps to know it's the Pythagoras Theorem with something extra so it works for all triangles:

So, to remember it:

• think " abc ": a 2 + b 2 = c 2 ,
• then a 2 nd " abc ": 2ab cos( C ) ,
• and put them together: a 2 + b 2 − 2ab cos(C) = c 2

When to Use

The Law of Cosines is useful for finding:

• the third side of a triangle when we know two sides and the angle between them (like the example above)
• the angles of a triangle when we know all three sides (as in the following example)

Example: What is Angle "C" ...?

The side of length "8" is opposite angle C , so it is side c . The other two sides are a and b .

Now let us put what we know into The Law of Cosines :

Now we use our algebra skills to rearrange and solve:

In Other Forms

Easier version for angles.

We just saw how to find an angle when we know three sides. It took quite a few steps, so it is easier to use the "direct" formula (which is just a rearrangement of the c 2 = a 2 + b 2 − 2ab cos(C) formula). It can be in either of these forms:

cos(C) = a 2 + b 2 − c 2 2ab

cos(A) = b 2 + c 2 − a 2 2bc

cos(B) = c 2 + a 2 − b 2 2ca

Example: Find Angle "C" Using The Law of Cosines (angle version)

In this triangle we know the three sides:

Use The Law of Cosines (angle version) to find angle C :

Versions for a, b and c

Also, we can rewrite the c 2 = a 2 + b 2 − 2ab cos(C) formula into a 2 = and b 2 = form.

Here are all three:

a 2 = b 2 + c 2 − 2bc cos(A)

b 2 = a 2 + c 2 − 2ac cos(B)

But it is easier to remember the " c 2 =" form and change the letters as needed.

As in this example:

Example: Find the distance "z"

The letters are different! But that doesn't matter. We can easily substitute x for a, y for b and z for c

Answer: z = 14.5

Did you notice that cos(131º) is negative and so the last term ends up positive (+ 80.17...)

The cosine of an obtuse angle is always negative (see Unit Circle ).

Chapter 3: Laws of Sines and Cosines

3.3 The Law of Cosines

Algebra refresher.

Solve each quadratic equation.

• [latex]2.5x^{2} + 6.2 = 816.2[/latex]
• [latex]0.8x^{2} - 124 = 376[/latex]
• [latex]2x(2x - 3) = 208[/latex]
• [latex]3x(x + 5) = 900[/latex]
• [latex]2x^{2} - 6x = 233.12[/latex]
• [latex]0.5x^{2} + 1.5x = 464[/latex]
• [latex]\pm 8[/latex]
• [latex]\pm 25[/latex]
• [latex]8[/latex], [latex]{-6.5}[/latex]
• [latex]15[/latex], [latex]{-20}[/latex]
• [latex]12.4[/latex], [latex]{-9.4}[/latex]
• [latex]29[/latex], [latex]{-32}[/latex]

Learning Objectives

• Use the law of cosines to find the side opposite an angle #7-12
• Use the law of cosines to find an angle #13-20
• Use the law of cosines to find a side adjacent to an angle #21-26
• Decide which law to use #27-34
• Solve a triangle #35-42
• Solve problems using the law of cosines #43-56

Law of Cosines

If we know two angles and one side of a triangle, we can use the law of sines to solve the triangle. We can also use the law of sines when we know two sides and the angle opposite one of them. But the law of sines is not helpful for the problem that opened this chapter, finding the distance from Avery to Clio. In this case we know two sides of the triangle, [latex]a[/latex] and [latex]c{,}[/latex] and the included angle, [latex]B{.}[/latex]

To solve a triangle when we know two sides and the included angle, we will need a generalization of the Pythagorean theorem known as the law of cosines. In a right triangle, with [latex]C = 90°{,}[/latex] the Pythagorean theorem tells us that [latex]c^{2} = a^{2} + b^{2}[/latex] If we allow angle [latex]C[/latex] to vary but keep [latex]a[/latex] and [latex]b[/latex] the same length, the side [latex]c[/latex] will grow or shrink, depending on whether we increase or decrease the angle [latex]C{,}[/latex] as shown below.

The Pythagorean theorem is actually a special case of a more general law that applies to all triangles, no matter what the size of angle [latex]C{.}[/latex] The equation relating the three sides of a triangle is [latex]c^{2} = a^{2} + b^{2} - 2ab \cos C[/latex] You can see that when [latex]C[/latex] is a right angle, [latex]\cos 90° = 0{,}[/latex] so the equation reduces to the Pythagorean theorem. We can write similar equations involving the angles or [latex]A[/latex] or [latex]B{.}[/latex] The three equations are all versions of the law of cosines.

Law of Cosines.

If the angles of a triangle are [latex]A, B{,}[/latex] and [latex]C{,}[/latex] and the opposite sides are, respectively, [latex]a, b,[/latex] and [latex]c{,}[/latex] then

[latex]{a^{2} = b^{2} + c^{2} - 2bc \cos A} \\ {b^{2} = a^{2} + c^{2} - 2ac \cos B} \\ {c^{2} = a^{2} + b^{2} - 2ab \cos C} [/latex]

For a proof of the law of cosines, see Homework Problems 57 and 58.

Finding a Side

Now we can solve the problem of the distance from Avery to Clio. Here is the figure from Section 3.1 showing the location of the three towns.

Example 3.39.

How far is it from Avery to Clio?

[latex]b^{2} = a^{2} + c^{2} - 2ac \cos B \qquad \text{Substitute the known values.}[/latex] [latex]b^{2} = 34^{2} + 48^{2} - 2(34)(48) \cos 125° \qquad \text{Simplify the right side}[/latex] [latex]b^{2} = 3460 - 3264 \cos 125° = 5332.153 \qquad \text{Take Square roots}[/latex] [latex]b = 73.02[/latex]

Avery is about [latex]73[/latex] miles from Clio.

Caution 3.40.

When simplifying the law of cosines, be careful to follow the order of operations. In the previous example, the right side of the equation [latex]b^{2} = 34^{2} + 48^{2} - 2(34)(48) \cos 125°[/latex]

has three terms and simplifies to

[latex]b^{2}=1156+2304-3264\cos 125^{o}[/latex]

[latex]b^{2} = 3460 - 3264(-0.573567364 ...)[/latex]

Note that [latex]3264[/latex] is the coefficient of [latex]\cos 125°{,}[/latex] so it would be incorrect to subtract [latex]3264[/latex] from [latex]3460[/latex]. If you are using a graphing calculator, you can enter the right side of the equation exactly as it is written.

Checkpoint 3.41.

In [latex]\triangle ABC{,}[/latex] [latex]a = 11,~c = 23{,}[/latex] and [latex]B = 87°{.}[/latex] Find [latex]b[/latex] and round your answer to two decimal places.

[latex]24.97[/latex]

Finding an Angle

We can also use the law of cosines to find an angle when we know all three sides of a triangle. Pay close attention to the algebraic steps used to solve the equation in the next example.

Example 3.42.

In the triangle at right, [latex]a = 6,~ b = 7{,}[/latex] and [latex]c = 11{.}[/latex] Find angle [latex]C{.}[/latex]

We choose the version of the law of cosines that uses angle [latex]C{.}[/latex] [latex]c^{2} = a^{2} + b^{2} - 2ab \cos C \qquad \text{Substitute the known values.}[/latex] [latex]11^{2} = 6^{2} + 7^{2} - 2 (6) (7) \cos \qquad \text{Simplify each side.}[/latex] [latex]121 = 36 + 49 - 84 \cos C \qquad \text{Isolate the cosine term.}[/latex] [latex]36 = -84 \cos C \qquad \text{Solve for cos C.}[/latex] [latex]\dfrac{-3}{7} = \cos C \qquad \text{Solve for C.}[/latex] [latex]C = \cos^{-1} (\dfrac{-3}{7}) = 115.4°[/latex] Angle [latex]C[/latex] is about [latex]115.4°{.}[/latex]

Checkpoint 3.43.

In [latex]\triangle ABC{,}[/latex] [latex]a = 5.3,~b = 4.7{,}[/latex] and [latex]c = 6.1{.}[/latex] Find angle [latex]B[/latex] and round your answer to two decimal places.

[latex]48.07°[/latex]

Once we have calculated one of the angles in a triangle, we can use either the law of sines or the law of cosines to find a second angle. Here is how we would use the law of sines to find angle [latex]A[/latex] in the previous example.

[latex]\dfrac{\sin A}{a} = \dfrac{\sin C}{c} \qquad \text{Substitute the known values.}[/latex] [latex]\dfrac{\sin A}{6} = \dfrac{\sin 115.4°}{11} \qquad\text{Solve for sin A.}[/latex] [latex]\sin A = 6 \cdot \dfrac{\sin 115.4°}{11} \approx 0.4928[/latex] Thus, [latex]A = \sin^{-1}(0.4928) = 29.5°{.}[/latex] (We know that [latex]A[/latex] is an acute angle because it is opposite the shortest side of the triangle.) Finally, [latex]B = 180° - (A + C) \approx 35.1°[/latex] Alternatively, we can use the law of cosines to find angle [latex]A{.}[/latex]

[latex]a^{2} = b^{2} + c^{2} - 2bc \cos A \qquad \text{Substitute the known values.}[/latex] [latex]6^{2} = 7^{2} + 11^{2} - 2(7) (11) \cos A \qquad \text{Simplify each side.}[/latex] [latex]36=49+121-154\cos A \qquad \text{Isolate the cosine term.}[/latex] [latex]-134 = -154 \cos A \qquad \text{Solve for cos A.}[/latex] [latex]\dfrac{67}{77} = \cos A \qquad \text{Solve for A.}[/latex] [latex]A = \cos^{-1} (\dfrac{67}{77}) = 29.5°[/latex]

Using the law of sines requires fewer calculations than the law of cosines, but the law of cosines uses only the original values instead of the results of our previous calculations and approximations.

Whenever we round off a number, we introduce inaccuracy into the calculations, and these inaccuracies grow with each additional calculation. Thus, for the sake of accuracy, it is best to use given values in preference to calculated values whenever possible.

Using the Law of Cosines for the Ambiguous Case

In Section 3.2 we encountered the ambiguous case:

If we know two sides [latex]a[/latex] and [latex]b[/latex] of a triangle and the acute angle [latex]\alpha[/latex] opposite one of them, there may be one solution, two solutions, or no solution, depending on the size of [latex]a[/latex] in relation to [latex]b[/latex] and [latex]\alpha{,}[/latex] as shown below.

The Ambiguous Case.

If [latex]\alpha[/latex] is an obtuse angle, things are simpler: there is one solution if [latex]a \gt b[/latex] and no solution if [latex]a \le b{.}[/latex]

Because there are always two angles with a given sine, if we use the law of sines for the ambiguous case, we must check whether both possible angles result in a triangle. But here is another approach: We can apply the law of cosines to find the third side first. With that method, we’ll need the quadratic formula.

Quadratic Formula.

The solutions of the quadratic equation [latex]ax^{2} + bx + c = 0,~~a not= 0,[/latex] are given by [latex]x = \dfrac{-b^ {\pm} \sqrt{b^{2} - 4ac}}{2a}[/latex]

A quadratic equation can have one solution, two solutions, or no solution, depending on the value of the discriminant , [latex]b^{2} - 4ac{.}[/latex] If we use the law of cosines to find a side in the ambiguous case, the quadratic formula will tell us how many triangles have the given properties.

• If the quadratic equation has one positive solution, there is one triangle.
• If the quadratic equation has two positive solutions, there are two triangles.
• If the quadratic equation has no positive solutions, there is no triangle with the given properties.

Example 3.45.

In [latex]\triangle ABC,~ B = 14.4°,~ a = 8{,}[/latex] and [latex]b = 3{.}[/latex] Solve the triangle.

We begin by finding the third side of the triangle. Using the law of cosines, we have [latex]b^{2} = a^{2} + c^{2} - 2ac \cos B \qquad \text{Substitute the known values.}[/latex] [latex]3^{2} = 8^{2} + c^{2} - 2(8)c \cos 14.4° \qquad \text{Simplify.}[/latex] [latex]9 = 64 + c^{2} - 16c (0.9686) \qquad \text{Write the quadratic equation in standard form.}[/latex] [latex]0 = c^{2}-15.497c + 55 \qquad \text{Apply the quadratic formula.}[/latex]

[latex]c = \dfrac{15.497^ {\pm} \sqrt {(-15.497)^{2}} - 4(1)(55)}{2(1)} \qquad \text{Simplify.}[/latex] [latex]= \dfrac{15.497^ {\pm} 4.490}{2} = 5.503~ { or }~ 9.994[/latex]

Because there are two positive solutions for side [latex]c{,}[/latex] either [latex]c = 5.503[/latex] or [latex]c = 9.994{,}[/latex] there are two triangles with the given properties. We apply the law of cosines again to find angle [latex]C[/latex] in each triangle.

For the triangle with [latex]c = 5.503{,}[/latex] we have [latex]c^{2} = a^{2} + b^{2} - 2ab \cos C \qquad \text{Substitute the known values.}[/latex] [latex]5.503^{2} = 8^{2} + 3^{2} - 2(8)(3) \cos C \qquad \text{Solve for cos C}[/latex] [latex]\cos C = \dfrac{5.503^{2} - 64 - 9}{-48} = 0.889876[/latex] [latex]C = \cos^{-1} 0.889876 = 27.1°[/latex] and [latex]A = 180° - (14.4° + 27.1°) = 138.5°{.}[/latex] For the triangle with [latex]c = 9.994{,}[/latex] we have [latex]c^{2} = a^{2} + b^{2} - 2ab \cos C \qquad \text{Substitute the known values.}[/latex] [latex]9.994^{2} = 8^{2} + 3^{2} - 2(8)(3) \cos C. \text{Solve for cos C.}[/latex] [latex]\cos C = \dfrac{9.994^{2} - 64 - 9}{-48} = -0.560027[/latex] [latex]C = \cos^{-1} (-0.560027) = 124.1°[/latex]

In the previous example, notice that we used the law of cosines instead of the law of sines to find a second angle in the triangle because there is only one angle between [latex]0°[/latex] and [latex]180°[/latex] with a given cosine. We don’t have to check the results, as we would if we used the law of sines.

Checkpoint 3.47.

Use the law of cosines to find all triangles [latex]\triangle ABC[/latex] with [latex]\angle A = 48°,~ a = 10{,}[/latex] and [latex]b = 15{.}[/latex]

No solution

Even with the aid of GPS (global positioning system) instruments, aircraft pilots and ship captains need to understand navigation based on trigonometry.

Example 3.48.

The sailing club leaves the marina on a heading [latex]15°[/latex] east of north and sails for [latex]18[/latex] miles. They then change course, and after traveling for [latex]12[/latex] miles on a heading [latex]35°[/latex] east of north, they experience engine trouble and radio for help. The marina sends a speedboat to rescue them. How far should the speedboat go, and on what heading?

Next, we apply the law of cosines again to find [latex]\angle A{.}[/latex]

[latex]a^{2} = b^{2} + c^{2} - 2bc \cos A \qquad \text{Substitute the known values.}[/latex] [latex]12^{2} = 29.56^{2} + 18^{2} - 2(29.56)(18) \cos A \qquad \text{Solve for cos A.}[/latex] [latex]\cos A = \dfrac{12^{2} - 29.56^{2} - 18^{2}}{-2(29.56)(18)} = 0.9903[/latex] [latex]C = \cos^{-1} (0.9903) = 8°[/latex] Thus, [latex]x = 29.56[/latex] and [latex]\theta = 8° + 15° = 23°{.}[/latex] The speedboat should travel 29.56 miles on a heading [latex]23°[/latex] east of north.

Checkpoint 3.49.

Howard wants to fly from Anchorage to Nome, Alaska, a distance of 540 miles on a heading [latex]57°[/latex] west of north. After flying for some time, he discovers that his heading is in error, and he is actually flying [latex]47°[/latex] west of north. Howard corrects his flight plan and changes course when he is exactly 200 miles from Anchorage. What is his new heading, and how far is he from Nome?

[latex]62.8°[/latex] west of north, 344.8 miles

Which Law to Use

How can we decide which law, the law of sines or the law of cosines, is appropriate for a given problem?

• If we are solving a right triangle, we don’t need the Laws of Sines and cosines; all we need are the definitions of the trigonometric ratios.
• But for oblique triangles, we can identify the following cases:

How to Solve an Oblique Triangle.

In the ambiguous case, SSA, the law of sines is easier to apply, but there will be two possible angles, and we must check each angle to see if it produces a solution. Using the law of cosines involves solving a quadratic equation, but each positive solution of the equation yields a solution of the triangle.

Example 3.51.

We know two sides of the triangle and the angle opposite one of them. We can use the law of sines to find [latex]\angle B{.}[/latex] [latex]\dfrac{\sin B}{6} = \dfrac{\sin 40°}{10}[/latex] [latex]\sin B = 0.3857[/latex]

This is the ambiguous case; there are two angles between [latex]0°[/latex] and [latex]180°[/latex] with sine [latex]0.3857{,}[/latex] and we must check each angle to see if it produces a solution.

If instead we start by finding side [latex]c{,}[/latex] we use the law of cosines.

[latex]10^{2} = 6^{2} + c^{2} - 2(6)c \cos 40°[/latex] [latex]c^{2} - (12 \cos 40°)c - 64 = 0[/latex] [latex]c = \dfrac {12 \cos 40°^ {\pm} \sqrt {(-12 \cos 40°)^{2} - 4(1)(-64)}}{2(1)}[/latex] You can check that the quadratic equation has only one positive solution for [latex]c[/latex] (or notice that because [latex]a \gt b{,}[/latex] angle [latex]B[/latex] must be acute).

Checkpoint 3.52.

In the triangle at right, which part of the triangle can you find, and which law should you use?

We first find side [latex]c[/latex] using the law of cosines

Section 3.3 Summary

• Quadratic equation
• Quadratic formula
• Discriminant

 Concepts

• The law of sines is not helpful when we know two sides of the triangle and the included angle. In this case we need the law of cosines.

Law of cosines: If the angles of a triangle are [latex]A, B{,}[/latex] and [latex]C{,}[/latex] and the opposite sides are, respectively, [latex]a, b,[/latex] and [latex]c{,}[/latex] then [latex]a^{2} = b^{2} + c^{2} - 2bc \cos A[/latex] [latex]b^{2} = a^{2} + c^{2} - 2ac \cos B[/latex] [latex]c^{2} = a^{2} + b^{2} - 2ab \cos C[/latex]

• We can also use the law of cosines to find an angle when we know all three sides of a triangle.
• We can use the law of cosines to solve the ambiguous case.

 Study Questions

• The law of cosines is really a generalization of what familiar theorem?
• If you know all three sides of a triangle and one angle, what might be the advantage in using the law of cosines to find another angle instead of the law of sines?
• State the quadratic formula from memory. Try to sing the quadratic formula to the tune of “Pop Goes the Weasel.”
• Francine is solving a triangle in which [latex]a = 20,~ b = 16{,}[/latex] and [latex]\angle A = 26°{.}[/latex] She finds that [latex]\sin B = 0.3507{.}[/latex] How does she know that [latex]\angle B = 20.5°{,}[/latex] and not [latex]159.5°{?}[/latex]

A polynomial equation with degree 2 is called quadratic. The graph of a quadratic is called a parabola.

It is simply written in the form \[ ax^2+bx + c = 0 \], where [latex]a \neq 0[/latex]

\[ x = \frac{-b \pm \sqrt{b^2-4ac}}{2a} \]

Discriminant \[ (D) = b^2 - 4ac \]

If the discriminant is greater than zero (D > 0), then the quadratic equation has two distinct real solutions. This means the graph of the equation intersects the x-axis at two different points.

If the discriminant is equal to zero (D = 0), then the quadratic equation has one real solution. If the discriminant is less than zero (D < 0), then the quadratic equation has no real solutions.

Trigonometry Copyright © 2024 by Bimal Kunwor; Donna Densmore; Jared Eusea; and Yi Zhen. All Rights Reserved.

Share This Book

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons

Margin Size

• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

4.1.1: Laws of Sines and Cosines

• Last updated
• Save as PDF
• Page ID 4154

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)

( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

\( \newcommand{\Span}{\mathrm{span}}\)

\( \newcommand{\id}{\mathrm{id}}\)

\( \newcommand{\kernel}{\mathrm{null}\,}\)

\( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\)

\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\)

\( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)

\( \newcommand{\vectorA}[1]{\vec{#1}}      % arrow\)

\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}}      % arrow\)

\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vectorC}[1]{\textbf{#1}} \)

\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)

\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)

\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)

Solving for parts of non-right triangles using trigonometry.

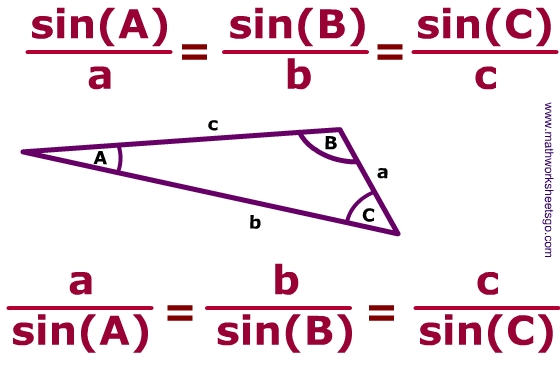
Law of Sines: If \(\Delta ABC\) has sides of length, \(a\), \(b\), and \(c\), then \(\dfrac{\sin A}{a}=\dfrac{\sin B}{b}=\dfrac{\sin C}{c}\).

Looking at a triangle, the lengths a,b, and c are opposite the angles of the same letter.

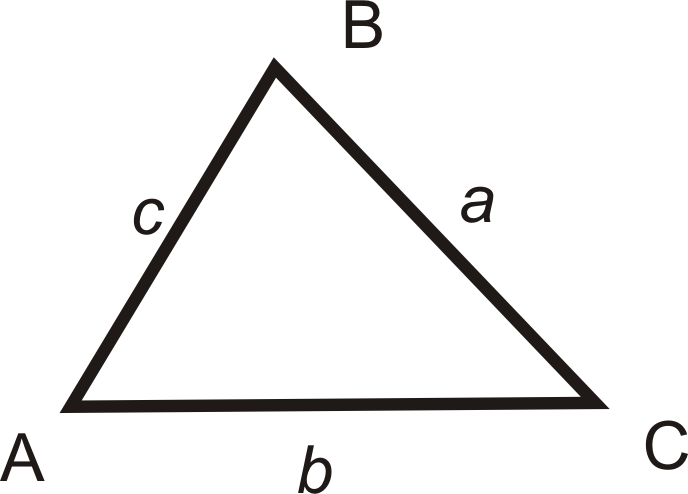
Use Law of Sines when given:

• An angle and its opposite side.
• Any two angles and one side.

Two sides and the non-included angle.

Law of Cosines: If \(\Delta ABC\) has sides of length \(a\),\(b\), and \(c\), then:

\(\begin{aligned} a^2&=b^2+c^2−2bc\cos A \\ b^2&=a^2+c^2−2ac \cos B \\ c^2&=a^2+b^2−2ab \cos C \end{aligned}\)

Even though there are three formulas, they are all very similar. First, notice that whatever angle is in the cosine, the opposite side is on the other side of the equal sign.

Use Law of Cosines when given:

• Two sides and the included angle.
• All three sides.

Using the Law of Sines

1. Solve the triangle using the Law of Sines . Round decimal answers to the nearest tenth.

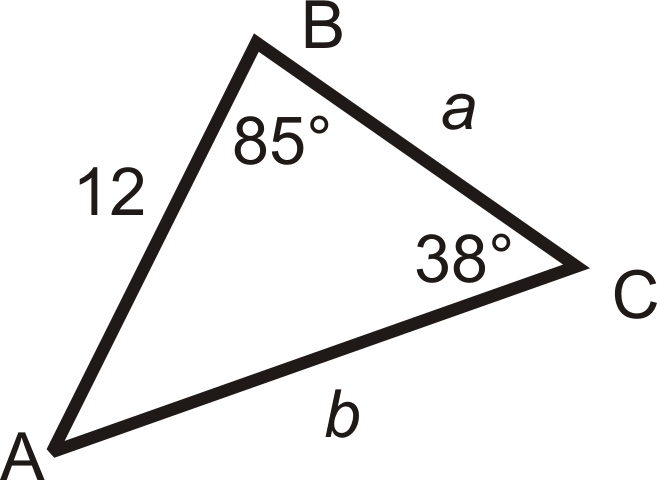
First, to find \(m\angle A\), we can use the Triangle Sum Theorem.

\(\begin{aligned} m\angle A+85^{\circ} +38^{\circ}&=180^{\circ} \\ m\angle A&=57^{\circ} \end{aligned}\)

Now, use the Law of Sines to set up ratios for \(a\) and \(b\).

\(\dfrac{\sin 57^{\circ} }{a}=\dfrac{\sin 85^{\circ} }{b}=\dfrac{\sin 38^{\circ} }{12}\)

\(\begin{aligned} \dfrac{\sin 57^{\circ}}{a} &=\dfrac{\sin 38^{\circ}}{12} & \dfrac{\sin 85^{\circ}}{b} &=\dfrac{\sin 38^{\circ}}{12} \\ a \cdot \sin 38^{\circ} &=12 \cdot \sin 57^{\circ} & b \cdot \sin 38^{\circ} &=12 \cdot \sin 85^{\circ} \\ a &=\dfrac{12 \cdot \sin 57^{\circ}}{\sin 38^{\circ}} \approx 16.4 & \quad b &=\dfrac{12 \cdot \sin 85^{\circ}}{\sin 38^{\circ}} \approx 19.4 \end{aligned}\)

2. Solve the triangle using the Law of Sines. Round decimal answers to the nearest tenth.

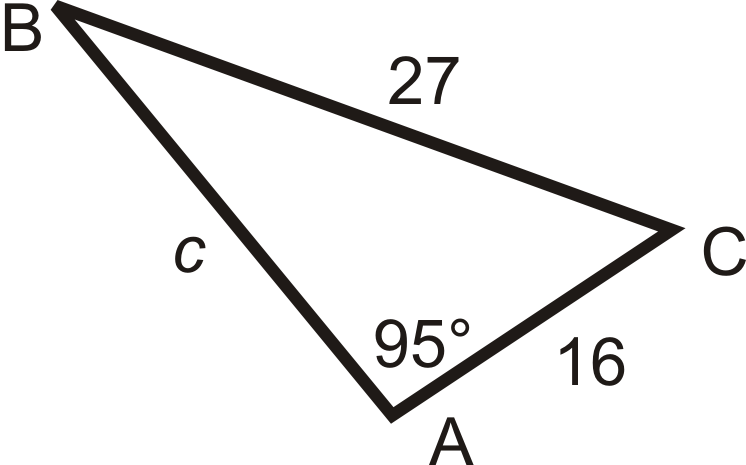
Set up the ratio for \(\angle B\) using Law of Sines.

\(\begin{aligned} \dfrac{\sin 95^{\circ} }{27}&=\dfrac{\sin B}{16} \\ 27\cdot \sin B&=16\cdot \sin 95^{\circ} \\ \sin B&=\dfrac{16\cdot \sin 95^{\circ} }{27}\rightarrow\sin ^{−1}\left(\dfrac{16\cdot \sin 95^{\circ} }{27} \right) =36.2^{\circ} \end{aligned}\)

To find \(m\angle C\) use the Triangle Sum Theorem.

\(m\angle C+95^{\circ} +36.2^{\circ} =180^{\circ} \rightarrow m\angle C=48.8^{\circ}\)

To find \(c\), use the Law of Sines again. \(\dfrac{\sin 95^{\circ} }{27}=\dfrac{\sin 48.8^{\circ} }{c}\)

\(\begin{aligned} c\cdot \sin 95^{\circ}&=27\cdot \sin 48.8^{\circ} \\ c&=27\cdot \sin 48.8^{\circ} \sin 95^{\circ} \approx 20.4 \end{aligned}\)

Using the Law of Cosines

Solve the triangle using Law of Cosines . Round your answers to the nearest hundredth.

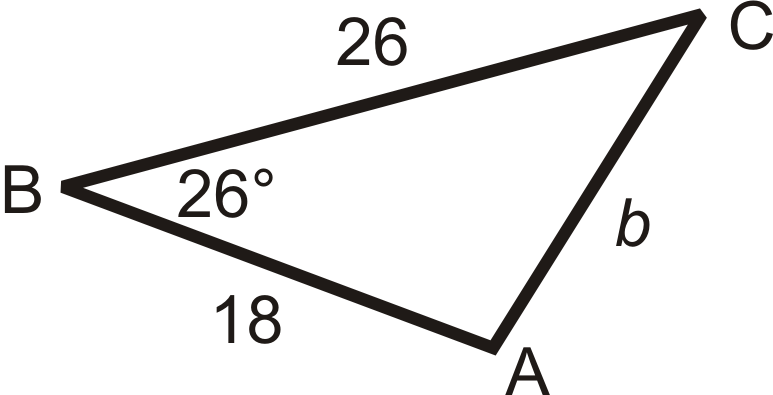
Use the second equation to solve for \(\angle B\).

\(\begin{aligned} b^2&=26^2+18^2−2(26)(18)\cos 26^{\circ} \\ b^2&=1000−936\cos 26^{\circ} \\ b^2&=158.7288 \\ b&\approx 12.60 \end{aligned}\)

To find \(m\angle A\) or \(m\angle C\), you can use either the Law of Sines or Law of Cosines . Let’s use the Law of Sines.

\(\begin{aligned} \dfrac{\sin 26^{\circ} }{12.60}&=\dfrac{\sin A}{18} \\ 12.60\cdot \sin A&=18\cdot \sin 26^{\circ} \\ \sin A&=18\cdot \sin 26^{\circ} 12.60 \end{aligned}\)

\(\sin ^{−1} \left(18\cdot \sin 26^{\circ} 12.60 \right)\approx 38.77^{\circ} \) To find \(m\angle C\), use the Triangle Sum Theorem.

\(\begin{aligned} 26^{\circ} +38.77^{\circ} +m\angle C&=180^{\circ} \\ m\angle C&=115.23^{\circ} \end{aligned}\)

Find the following angles in the triangle below. Round your answers to the nearest hundredth.

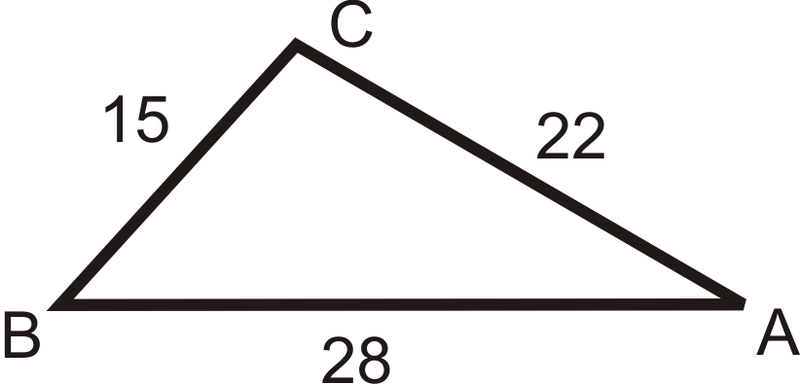
Example \(\PageIndex{1}\)

\(m\angle A\)

When you are given only the sides, you have to use the Law of Cosines to find one angle and then you can use the Law of Sines to find another.

\(\begin{aligned} 15^2&=22^2+28^2−2(22)(28)\cos A \\ 225&=1268−1232\cos A \\ −1043&=−1232\cos A \\ \dfrac{−1043}{−1232}&=\cos A \rightarrow \cos ^{−1}\left(\dfrac{1043}{1232}\right) \approx 32.16^{\circ}\end{aligned}\)

Example \(\PageIndex{2}\)

\(m\angle B\)

Now that we have an angle and its opposite side, we can use the Law of Sines.

\(\begin{aligned} \dfrac{\sin 32.16^{\circ} }{15} &=\dfrac{\sin B}{22} \\ 15\cdot \sin B &=22\cdot \sin 32.16^{\circ} \\ \sin B &=\dfrac{22\cdot \sin 32.16^{\circ} }{15} \end{aligned}\)

\(\sin ^{−1}\left(\dfrac{22\cdot \sin 32.16^{\circ} }{15}\right)\approx 51.32^{\circ} \).

Example \(\PageIndex{3}\)

\(m\angle C\)

To find \(m\angle C\), use the Triangle Sum Theorem.

\(\begin{aligned} 32.16^{\circ} +51.32^{\circ} +m\angle C&=180^{\circ} \\ m\angle C&=96.52^{\circ} \end{aligned}\)

Use the Law of Sines or Cosines to solve \(\Delta ABC\). If you are not given a picture, draw one. Round all decimal answers to the nearest tenth.

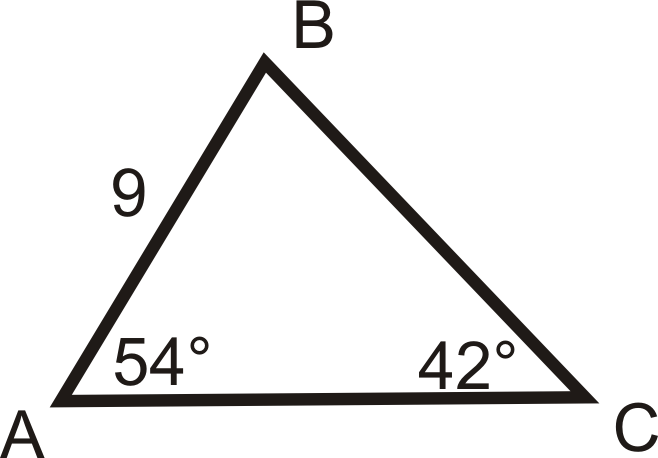
• \(m\angle A=74^{\circ} \), \(m\angle B=11^{\circ} \), \(BC=16\)
• \(m\angle A=64^{\circ} \), \(AB=29\), \(AC=34\)
• \(m\angle C=133^{\circ} \), \(m\angle B=25^{\circ} \),\(AB=48\)

Use the Law of Sines to solve \(\Delta ABC\) below.

• \(m\angle A=20^{\circ} \), \(AB=12\), \(BC=5\)

Recall that when we learned how to prove that triangles were congruent we determined that SSA (two sides and an angle not included) did not determine a unique triangle. When we are using the Law of Sines to solve a triangle and we are given two sides and the angle not included, we may have two possible triangles. Problem 14 illustrates this.

• Let’s say we have \(\Delta ABC\) as we did in problem 13. In problem 13 you were given two sides and the not included angle. This time, you have two angles and the side between them (ASA). Solve the triangle given that \(m\angle A=20^{\circ} \), \(m\angle C=125^{\circ}\), \(AC=8.4\)
• Does the triangle that you found in problem 14 meet the requirements of the given information in problem 13? How are the two different \(m\angle C\) related? Draw the two possible triangles overlapping to visualize this relationship.

Review (Answers)

To view the Review answers, open this PDF file and look for section 8.10.

Additional Resources

Video: The Law of Sines: The Basics

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons

Margin Size

• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

8.1.1: Non-Right Triangles - Laws of Sines and Cosines (Exercises)

• Last updated
• Save as PDF
• Page ID 22234

• David Lippman & Melonie Rasmussen
• The OpenTextBookStore

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)

( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

\( \newcommand{\Span}{\mathrm{span}}\)

\( \newcommand{\id}{\mathrm{id}}\)

\( \newcommand{\kernel}{\mathrm{null}\,}\)

\( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\)

\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\)

\( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)

\( \newcommand{\vectorA}[1]{\vec{#1}}      % arrow\)

\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}}      % arrow\)

\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vectorC}[1]{\textbf{#1}} \)

\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)

\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)

\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)

section 8.1 exercises

Solve for the unknown sides and angles of the triangles shown.

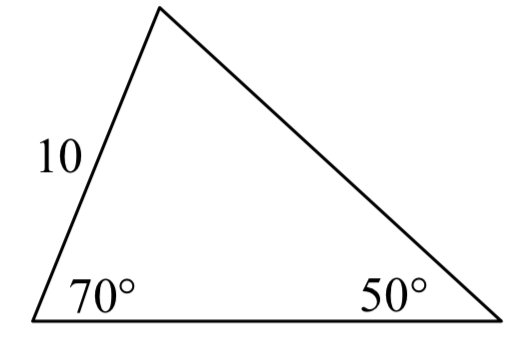
Assume \(\alpha\) is opposite side \(a\), \(\beta\) is opposite side \(b\), and \(\gamma\) is opposite side \(c\). Solve each triangle for the unknown sides and angles if possible. If there is more than one possible solution, give both.

9. \(\alpha = 43^{\circ}\), \(\gamma = 69^{circ}\), \(b = 20\)

10. \(\alpha = 35^{\circ}\), \(\gamma = 73^{circ}\), \(b = 19\)

11. \(\alpha = 119^{\circ}\), \(a = 26\), \(b = 14\)

12. \(\gamma = 113^{circ}\), \(b = 10\), \(c = 32\)

13. \(\beta = 50^{circ}\), \(a = 105\), \(b = 45\)

14. \(\beta = 67^{circ}\), \(a = 49\), \(b = 38\)

15. \(\alpha = 43.1^{circ}\), \(a = 184.2\), \(b = 242.8\)

16. \(\alpha = 36.6^{\circ}\), \(a = 186.2\), \(b = 242.2\)

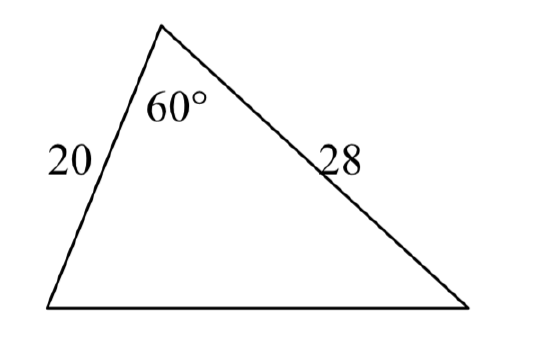
21. \(\gamma = 41.2^{\circ}\), \(a = 2.49\), \(b = 3.13\)

22. \(\beta = 58.7^{\circ}\), \(a = 10.6\), \(c = 15.7\)

23. \(\alpha = 120^{\circ}\), \(b = 6\), \(c = 7\)

24. \(\gamma = 115^{\circ}\), \(a = 18\), \(b = 23\)

25. Find the area of a triangle with sides of length 18, 21, and 32.

26. Find the area of a triangle with sides of length 20, 26, and 37.

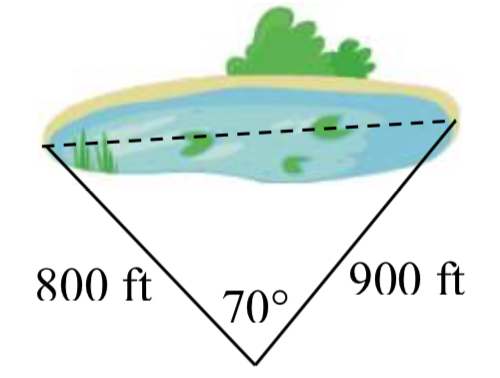
27. To find the distance across a small lake, a surveyor has taken the measurements shown. Find the distance across the lake.

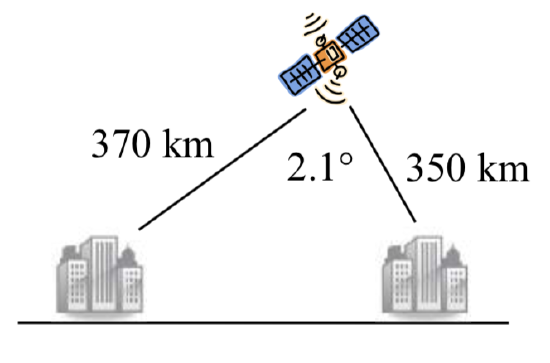
28. To find the distance between two cities, a satellite calculates the distances and angle shown (\(not to scale\)). Find the distance between the cities.

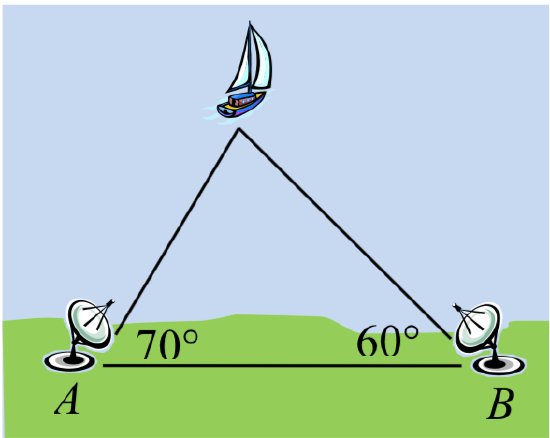
29. o determine how far a boat is from shore, two radar stations 500 feet apart determine the angles out to the boat, as shown. Find the distance of the boat from the station A , and the distance of the boat from shore.

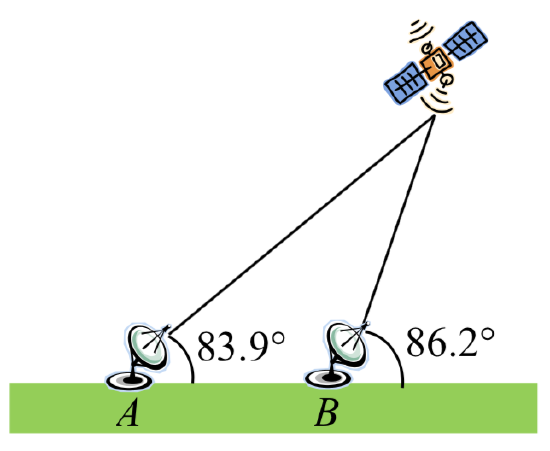
30. The path of a satellite orbiting the earth causes it to pass directly over two tracking stations \(A\) and \(B\), which are 69 mi apart. When the satellite is on one side of the two stations, the angles of elevation at \(A\) and \(B\) are measured to be \(86.2^{\circ}\) and \(83.9^{\circ}\), respectively. How far is the satellite from station \(A\) and how high is the satellite above the ground?

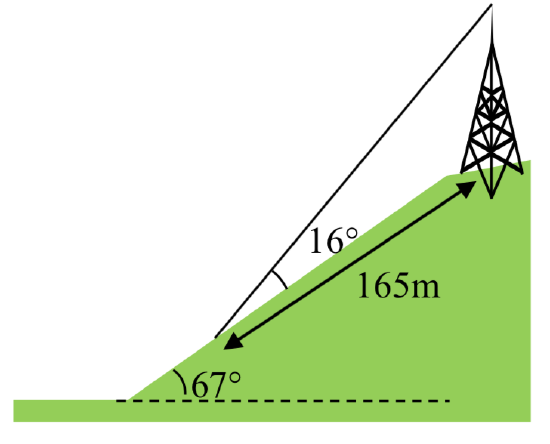
31. A communications tower is located at the top of a steep hill, as shown. The angle of inclination of the hill is \(67^{\circ}\). A guy-wire is to be attached to the top of the tower and to the ground, 165 m downhill from the base of the tower. The angle formed by the guy-wire and the hill is \(16^{\circ}\). Find the length of the cable required for the guy wire.

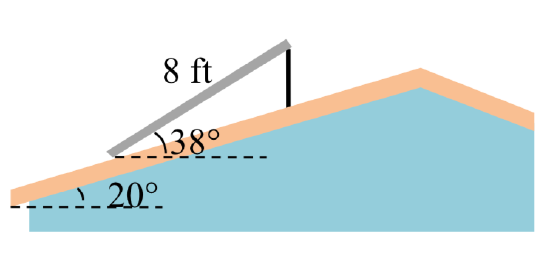
32. The roof of a house is at a \(20^{\circ}\) angle. An 8 foot solar panel is to be mounted on the roof, and should be angled \(38^{\circ}\) relative to the horizontal for optimal results. How long does the vertical support holding up the back of the panel need to be?

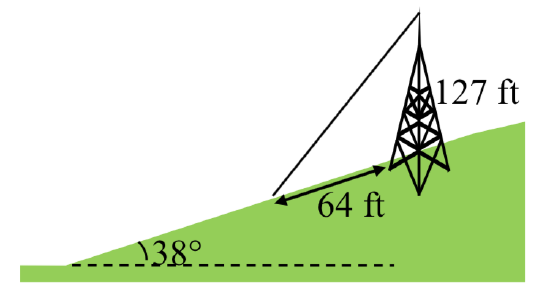
33. A 127 foot tower is located on a hill that is inclined \(38^{\circ}\) to the horizontal. A guy-wire is to be attached to the top of the tower and anchored at a point 64 feet downhill from the base of the tower. Find the length of wire needed.

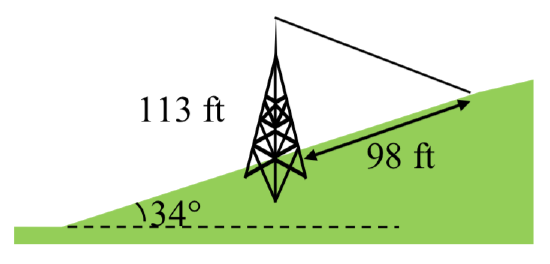
34. A 113 foot tower is located on a hill that is inclined \(34^{\circ}\) to the horizontal. A guy-wire is to be attached to the top of the tower and anchored at a point 98 feet uphill from the base of the tower. Find the length of wire needed.

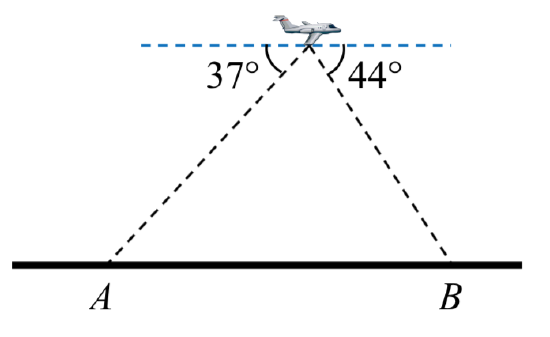
35. A pilot is flying over a straight highway. He determines the angles of depression to two mileposts, 6.6 km apart, to be \(37^{\circ}\) and \(44^{\circ}\), as shown in the figure. Find the distance of the plane from point \(A\), and the elevation of the plane.

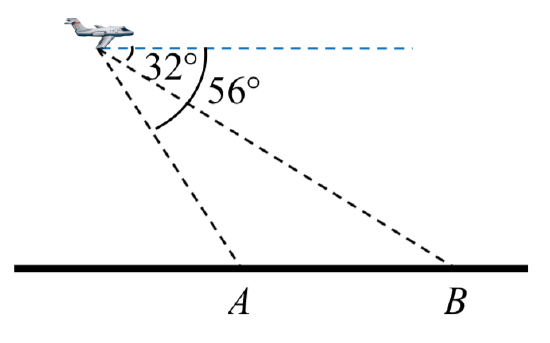
36. A pilot is flying over a straight highway. He determines the angles of depression to two mileposts, 4.3 km apart, to be \(32^{\circ}\) and \(56^{\circ}\), as shown in the figure. Find the distance of the plane from point \(A\), and the elevation of the plane.

37. To estimate the height of a building, two students find the angle of elevation from a point (at ground level) down the street from the building to the top of the building is \(39^{\circ}\). From a point that is 300 feet closer to the building, the angle of elevation (at ground level) to the top of the building is \(50^{\circ}\). If we assume that the street is level, use this information to estimate the height of the building.

38. To estimate the height of a building, two students find the angle of elevation from a point (at ground level) down the street from the building to the top of the building is \(35^{\circ}\). From a point that is 300 feet closer to the building, the angle of elevation (at ground level) to the top of the building is \(53^{\circ}\). If we assume that the street is level, use this information to estimate the height of the building.

39. A pilot flies in a straight path for 1 hour 30 min. She then makes a course correction, heading 10 degrees to the right of her original course, and flies 2 hours in the new direction. If she maintains a constant speed of 680 miles per hour, how far is she from her starting position?

40. Two planes leave the same airport at the same time. One flies at 20 degrees east of north at 500 miles per hour. The second flies at 30 east of south at 600 miles per hour. How far apart are the planes after 2 hours?

41. The four sequential sides of a quadrilateral have lengths 4.5 cm, 7.9 cm, 9.4 cm, and 12.9 cm. The angle between the two smallest sides is \(117^{\circ}\). What is the area of this quadrilateral?

42. The four sequential sides of a quadrilateral have lengths 5.7 cm, 7.2 cm, 9.4 cm, and 12.8 cm. The angle between the two smallest sides is \(106^{\circ}\). What is the area of this quadrilateral?

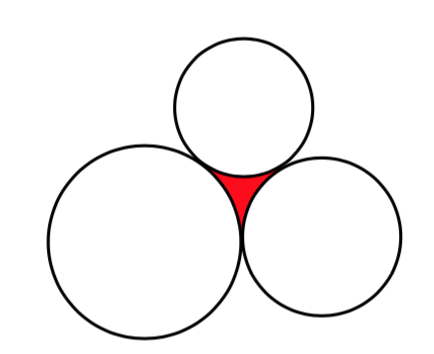
43. Three circles with radii 6, 7, and 8, all touch as shown. Find the shaded area bounded by the three circles.

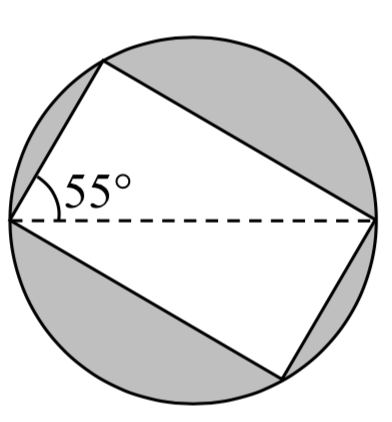
44. A rectangle is inscribed in a circle of radius 10 cm as shown. Find the shaded area, inside the circle but outside the rectangle.

9. \(\beta = 68^(\circ)\), \(a = 14.711\), \(c = 20.138\)

11. \(\beta = 28.096^(\circ)\), \(\gamma = 32.904^(\circ)\), \(c = 16.149\)

13. Not possible.

15. \(\beta = 64.243^(\circ)\), \(\gamma = 72.657^(\circ)\), \(c = 257.328\) OR \(\beta = 115.757^(\circ)\), \(\gamma = 21.143^(\circ)\), \(c = 97.238\)

21. \(c = 2.066\), \(\alpha = 52.545^(\circ)\), \(\beta = 86.255^(\circ)\)

23. \(\alpha = 11.269\), \(\beta = 27.457^(\circ)\), \(\gamma = 32.543^(\circ)\)

25. 177.562

27. 978.515 ft

29. Distance to A: 565.258ft. Distance to shore: 531.169 ft

31. 529.014

33. 173.877 feet

35. 4.642 km, 2.794 km

37. 757.963 ft

39. 2371.129 miles

41. 65.375 cm\(^(2)\)

If you're seeing this message, it means we're having trouble loading external resources on our website.

If you're behind a web filter, please make sure that the domains *.kastatic.org and *.kasandbox.org are unblocked.

To log in and use all the features of Khan Academy, please enable JavaScript in your browser.

Precalculus

Course: precalculus   >   unit 2.

• Solving for a side with the law of cosines

Solving for an angle with the law of cosines

• Solve triangles using the law of cosines
• Proof of the law of cosines

Want to join the conversation?

• Upvote Button navigates to signup page
• Downvote Button navigates to signup page
• Flag Button navigates to signup page

Video transcript

Lesson LAW OF COSINES

Law of Sines Worksheet

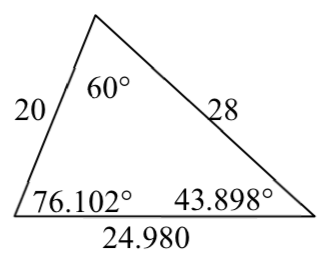
Students will practice applying the law of sines to calculate side lengths and angle measurements. This worksheet includes word problems as well as challenging bonus problems.

Example Questions

Visual Aids

Other Details

This is a 5 part worksheet:

• Part I Model Problems
• Part II Practice Problems (1-6)
• Part III Practice (harder) & Word Problems (7 - 18)
• Part IV Challenge Problems
• Part V Answer Key
• Pictures of Law of Sines (triangles, formula and more..)
• Law of Sines and Cosines Worksheets

Ultimate Math Solver (Free) Free Algebra Solver ... type anything in there!

Popular pages @ mathwarehouse.com.

• Math Lessons
• Math Formulas
• Calculators

Math Calculators, Lessons and Formulas

It is time to solve your math problem

• HW Help (paid service)
• Trigonometry

Law of Cosines

The law of cosines is used:.

1. to find the third side of a triangle when two sides and the included angle are given.

2. to find an angle when all 3 sides are given.

1. We are given $a$, $c$, and $\sphericalangle B$.

2. We are given sides $b$, $c$, and $\sphericalangle A$.

3. We are given sides $b$, $a$, and $\sphericalangle C$.

In triangle $ABC$, side $a= 8 cm$, $c = 10 cm$, and the angle at $B = 60^\circ$. Find side $b$, angle $A$ and angle $C$.

1. Side $b$:

2. Angle $A$

3. Angle $C$

• Roots and Radicals Simplify Expression Adding and Subtracting Multiplying and Dividing
• Complex Numbers Arithmetic Polar representation
• Polynomials Multiplying Polynomials Division of Polynomials Zeros of Polynomials
• Rational Expressions Simplifying Multiplying and Dividing Adding and Subtracting
• Solving Equations Linear Equations Absolute Value Equations Quadratic Equation Equations with Radicals
• Systems of Equations Substitution Method Elimination Method Row Reduction Cramers Rule Inverse Matrix Method
• Exponential Functions Introduction Exponential Equations Logarithmic Functions
• Trigonometry Trigonometric Formulas Trigonometric Equations Law of Cosines
• Progressions Arithmetic Progressions Geometric Progressions
• Differentiation Common formulas Product and Quotient Rule Chain Rule
• Limits Properties of Limits Rational Function Irrational Functions Trigonometric Functions L'Hospital's Rule
• Integrals Integration Formulas Exercises
• Integral techniques Substitution Integration by Parts Integrals with Trig. Functions Trigonometric Substitutions
• Integral Applications Area Volume Arc Length

Analytic geometry

• Analytic Geometry 2D Basic Concepts Lines Parallel and Perpendicular Lines Polar Coordinates
• Conic Sections Circle Ellipse Hyperbola
• Analytic Geometry 3D Line in 3D Planes

Linear Algebra

• Matrices Definitions Addition and Multiplication Gauss-Jordan elimination
• Determinants Introduction to Determinants Applications of Determinants
• Vectors Basic Operations Dot Product Cross Product

Random Quote

The essence of mathematics is its freedom.

Geoge Cantor

It is a mathematical fact that fifty percent of all doctors graduate in the bottom half of their class.

Author Unknown

Welcome to MathPortal. This website's owner is mathematician Miloš Petrović. I designed this website and wrote all the calculators, lessons, and formulas .

If you want to contact me, probably have some questions, write me using the contact form or email me on [email protected]

Email (optional)