Informative
Conversion Calculator
Follow Us On:
Truth Table Calculator
Write down a logical formula and the calculator will instantly compute truth table values for it, with the steps shown.
| Negation | ~ |
| Conjunction (AND) | & |
| Disjunction (OR) | v |
| Conditional | -> |
| Biconditional | <-> |
| Sheffer Stroke | | |
| Absurdity | # |
Add this calculator to your site

What is Truth Table?
Prepositional truth tables logic, how to make a truth table, connectives:.
- Negation/ NOT (¬)
- Implication / if-then (→)
- If and only if (⇔)
- Absurdity (#)
- Sheffer Stroke (|)
Propositional Equivalences
- The bi-conditional statement A⇔B is a tautology.
- The truth tables of every statement have the same truth variables.
| T | T | T | F | F | F | F |
| T | F | T | F | F | T | F |
| F | T | T | F | T | F | F |
| F | F | F | T | T | T | T |
How does Truth Table Calculator Works?
- First, enter a propositional logic equation with symbols.
- Hit the calculate button for results.
- Our calculator construct a truth table for 4 variables of the given expression.
One's Complement Calculator
Two's Complement Calculator
Venn Diagram Calculator
Decimal Calculator
Hex Calculator
Fraction to Decimal Calculator
Base Calculator
Add this calculator to your site.
Just copy a given code & paste it right now into your website HTML (source) for suitable page.
Give Us Your Feedback
Share Result

Get the ease of calculating anything from the source of calculator online
Email us at
© Copyrights 2024 by Calculator-Online.net
TruthTables
Logical operators
About truth tables
The best truth table generator on the web
Generate a truth table for a symbolic logic statement.
Compare two statements to determine if they are equivalent (always have the same outcome), contradictory (never have the same outcome), or neither.
Determine if an argument constructed of premises and a conclusion is valid (which means that if all of the premises are true, the conclusion is true), then construct a proof for the argument.
Logical operator quick reference
The first step in making a truth table is to translate your argument into the language of symbolic logic. Here's a logic translation cheat sheet to help out.
| Symbol | Alternative | Name | Kind | English connectives |
| ~ | ! | Tilde | Negation (NOT) | it is not the case that A; not A; it is false that A |
| & | &&, /\ | Ampersand | Conjunction (AND) | A and B; A but B; A yet B; A while B; A moreover B; A however B; A nonetheless B; A still B; A nevertheless B; A also B; A although B; both A and B; A additionally B; A furthermore B |
| v | ||, \/ | Wedge | Disjunction (OR) | A or B; A unless B |
| ⊃ | > | Horseshoe | Conditional (IF) | if A, then B; B only if A; A is a necessary condition for B; B is a necessary condition for A; B given that A; B provided that A; A implies that B; B on condition that A; B in case that A |
| ≡ | ==, = | Triple bar | Biconditional (IFF) | A if and only if B; A just in case that B; A is a necessary and sufficient condition for B; A is equivalent to B |
What is a truth table?
A truth table is a table that you can use to work with logic statements. Wikipedia says that:
But that's not very helpful if you're not already a logician. Basically, a truth table shows all of the possible inputs and outputs of a logic statement.
What's a symbolic logic statement?
A symbolic logic statement is a way to represent a logical argument with symbols. So, you could write something like this:
into something like this:
To translate this into symbolic logic, we turned each of the atomic statements of the statement into single letter constants, and words like or and and into the corresponding logical operators ( v and & ). You can find a list of all logical operators here .

How to use a truth table?
To summarize, to make and use a truth table:
- Translate your statement into symbolic logic
- Paste your statement into the calculator to generate the truth table
- Find the row on the table where the values of the identifiers match your input values
- Read the value in the main operator column (highlighted) to see the result!
Are truth tables hard?
Truth tables can seem a bit intimidating at first, but once you get the hang of how to use them they're very straightforward. Using them is just a matter of plugging in values and finding the corresponding row.
Why are truth tables useful?
Truth tables allow you to easily analyze a logical statement. It allows you to see the output of the statement for all combinations of inputs, which is helpful if the statement is very complicated and difficult to manually evaluate.
What are some other terms for symbolic logic?
Symbolic logic can also be referred to as "formal logic," or more broadly, "mathematical logic." You can view more synonyms on Power Thesaurus (an excellent thesaurus site).
- AI Math Solver Graphing Calculator Popular Problems Worksheets Study Guides Cheat Sheets Calculators Verify Solution
- Solutions Integral Calculator Derivative Calculator Algebra Calculator Matrix Calculator More...
- Graphing Line Graph Exponential Graph Quadratic Graph Sine Graph More...
- Calculators BMI Calculator Compound Interest Calculator Percentage Calculator Acceleration Calculator More...
- Geometry Pythagorean Theorem Calculator Circle Area Calculator Isosceles Triangle Calculator Triangles Calculator More...
- Tools Notebook Groups Cheat Sheets Worksheets Study Guides Practice Verify Solution
| x^{\msquare} | \log_{\msquare} | \sqrt{\square} | \nthroot[\msquare]{\square} | \le | \ge | \frac{\msquare}{\msquare} | \cdot | \div | x^{\circ} | \pi | |||||||||||
| \left(\square\right)^{'} | \frac{d}{dx} | \frac{\partial}{\partial x} | \int | \int_{\msquare}^{\msquare} | \lim | \sum | \infty | \theta | (f\:\circ\:g) | f(x) | |||||||||||
| ▭\:\longdivision{▭} | \times \twostack{▭}{▭} | + \twostack{▭}{▭} | - \twostack{▭}{▭} | \left( | \right) | \times | \square\frac{\square}{\square} |
- Pre Algebra Order of Operations Factors & Primes Fractions Long Arithmetic Decimals Exponents & Radicals Ratios & Proportions Percent Modulo Number Line Expanded Form Mean, Median & Mode
- Algebra Equations Inequalities System of Equations System of Inequalities Basic Operations Algebraic Properties Partial Fractions Polynomials Rational Expressions Sequences Power Sums Interval Notation Pi (Product) Notation Induction Prove That Logical Sets Word Problems
- Pre Calculus Equations Inequalities Scientific Calculator Scientific Notation Arithmetics Complex Numbers Coterminal Angle Polar/Cartesian Simultaneous Equations System of Inequalities Polynomials Rationales Functions Arithmetic & Comp. Coordinate Geometry Plane Geometry Solid Geometry Conic Sections Trigonometry
- Calculus Derivatives Derivative Applications Limits Integrals Integral Applications Integral Approximation Series ODE Multivariable Calculus Laplace Transform Taylor/Maclaurin Series Fourier Series Fourier Transform
- Functions Line Equations Functions Arithmetic & Comp. Conic Sections Transformation
- Linear Algebra Matrices Vectors
- Trigonometry Identities Proving Identities Trig Equations Trig Inequalities Evaluate Functions Simplify
- Statistics Mean Geometric Mean Quadratic Mean Average Median Mode Order Minimum Maximum Probability Mid-Range Range Standard Deviation Variance Lower Quartile Upper Quartile Interquartile Range Midhinge Standard Normal Distribution
- Physics Mechanics
- Chemistry Chemical Reactions Chemical Properties
- Finance Simple Interest Compound Interest Present Value Future Value
- Economics Point of Diminishing Return
- Conversions Roman Numerals Radical to Exponent Exponent to Radical To Fraction To Decimal To Mixed Number To Improper Fraction Radians to Degrees Degrees to Radians Hexadecimal Scientific Notation Distance Weight Time Volume
- Pre Algebra
- One-Step Addition
- One-Step Subtraction
- One-Step Multiplication
- One-Step Division
- One-Step Decimals
- Two-Step Integers
- Two-Step Add/Subtract
- Two-Step Multiply/Divide
- Two-Step Fractions
- Two-Step Decimals
- Multi-Step Integers
- Multi-Step with Parentheses
- Multi-Step Rational
- Multi-Step Fractions
- Multi-Step Decimals
- Solve by Factoring
- Completing the Square
- Quadratic Formula
- Biquadratic
- Logarithmic
- Exponential
- Rational Roots
- Floor/Ceiling
- Equation Given Roots
- Equation Given Points
- Newton Raphson
- Substitution
- Elimination
- Cramer's Rule
- Gaussian Elimination
- System of Inequalities
- Perfect Squares
- Difference of Squares
- Difference of Cubes
- Sum of Cubes
- Polynomials
- Distributive Property
- FOIL method
- Perfect Cubes
- Binomial Expansion
- Negative Rule
- Product Rule
- Quotient Rule
- Expand Power Rule
- Fraction Exponent
- Exponent Rules
- Exponential Form
- Logarithmic Form
- Absolute Value
- Rational Number
- Powers of i
- Complex Form
- Partial Fractions
- Is Polynomial
- Leading Coefficient
- Leading Term
- Standard Form
- Complete the Square
- Synthetic Division
- Linear Factors
- Rationalize Denominator
- Rationalize Numerator
- Identify Type
- Convergence
- Interval Notation
- Pi (Product) Notation
- Boolean Algebra
- Truth Table
- Mutual Exclusive
- Cardinality
- Caretesian Product
- Age Problems
- Distance Problems
- Cost Problems
- Investment Problems
- Number Problems
- Percent Problems
- Addition/Subtraction
- Multiplication/Division
- Dice Problems
- Coin Problems
- Card Problems
- Pre Calculus
- Linear Algebra
- Trigonometry
- Conversions
| x^{\msquare} | \log_{\msquare} | \sqrt{\square} | \nthroot[\msquare]{\square} | \le | \ge | \frac{\msquare}{\msquare} | \cdot | \div | x^{\circ} | \pi | |||||||||||
| \left(\square\right)^{'} | \frac{d}{dx} | \frac{\partial}{\partial x} | \int | \int_{\msquare}^{\msquare} | \lim | \sum | \infty | \theta | (f\:\circ\:g) | f(x) | |||||||||||
| - \twostack{▭}{▭} | \lt | 7 | 8 | 9 | \div | AC |
| + \twostack{▭}{▭} | \gt | 4 | 5 | 6 | \times | \square\frac{\square}{\square} |
| \times \twostack{▭}{▭} | \left( | 1 | 2 | 3 | - | x |
| ▭\:\longdivision{▭} | \right) | . | 0 | = | + | y |
Number Line
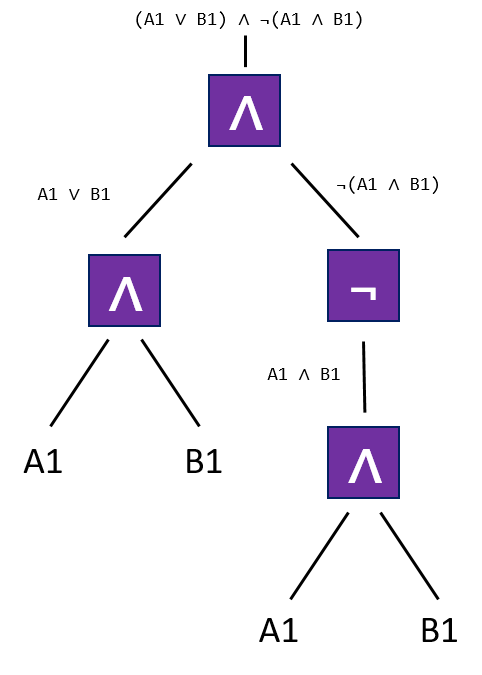
- truth\:table\:A\vee B
- truth\:table\:A\wedge B
- truth\:table\:\neg A\vee B
- truth\:table\:(A \wedge \neg B) \vee (C \wedge B)
truth-table-calculator
- Middle School Math Solutions – Inequalities Calculator Next up in our Getting Started maths solutions series is help with another middle school algebra topic - solving...
We want your feedback
Please add a message.
Message received. Thanks for the feedback.
Truth Table
Input syntax, here you can see which connectives we support and how you can enter them..
| Operator | Unicode | Alternatives |
|---|---|---|
| Negation | ¬ | !, ~ |
| Conjunction | ∧ | &, && |
| NAND | ⊼ | ¬∧, ¬&, ¬&&, !∧, !&, !&&, ~∧, ~&, ~&& |
| Disjunction | ∨ | |, || |
| NOR | ⊽ | ¬∨, ¬|, ¬||, !∨, !|, !||, ~∨, ~|, ~|| |
| Conditional | → | >, ->, => |
| Biconditional | ↔ | =, ==, <>, <=>, <-> |
| Exclusive Disjunction | ⇹ | !=, <!>, <!=> |
You can also enter multiple expressions by entering them comma separated: A∧B,A∨B

Tool to generate logical truth tables. In Boolean algebra or electronics, logical truth tables allow defining a function / gate / element / component according to its inputs and outputs.
Truth Table - dCode
Tag(s) : Symbolic Computation, Electronics
dCode is free and its tools are a valuable help in games, maths, geocaching, puzzles and problems to solve every day! A suggestion ? a feedback ? a bug ? an idea ? Write to dCode !
Please, check our dCode Discord community for help requests! NB: for encrypted messages, test our automatic cipher identifier !
Feedback and suggestions are welcome so that dCode offers the best 'Truth Table' tool for free! Thank you!
- Truth Table
- Mathematics
- Symbolic Computation
- Truth Table Generator
- Find Equation from Truth Table
Indicate only the output values of the function (the last column from the boolean truth table)
| |
| |
Answers to Questions (FAQ)
- What is a truth table? (Definition)
A truth table is a table representing the output boolean values of a logical expression based on their entries. The table thus displays all the possible combinations of the $ n $ input logical variables (generally 0 / FALSE and 1 / TRUE over $ n $ columns) and the result of the equation as output (last column).
| A | NOT A |
|---|---|
| 0 | 1 |
| 1 | 0 |
Every electronic circuit is associated with a truth table which describes it.
Usually the array starts with input values at $ 0 $ and ends with input values at $ 1 $ but sometimes it's reversed.
- How does the truth table calculator work?
dCode truth table generator interprets the Boolean logical expression and calculates (using Boolean algebra ) all the possible combinations of 0 and 1 for each variable (among the Boolean variables requested) in order to make the truth table .
dCode also makes it possible to find the Boolean logic function/expression from a truth table .
- How to find the equation from the truth table?
The only important column of the truth table is the last one, which describes the output values (the first columns are always identical for a given number of inputs) and which allows to convert into the Boolean expression .
There are 2 methods to find the Boolean equation from the truth table , either by using the output values 0 (calculation of Maxterms ) or by using output values 1 (calculation of Minterms ).
| input A | input B | output X |
|---|---|---|
| 0 | 0 | |
| 0 | 1 | |
| 1 | 0 | |
| 1 | 1 |
Here are the different calculations (which give the same result for the given example)
Calculation from the output values 1 of the truth table ( Minterms ): for each 1 , write the corresponding input values separated by logical AND , then group these results with a logical OR .
Example: Rows 2 and 3 are equal to 1 , row 2 is written as A AND NOT(B) (because A is 1 and B is 0 ), row 3 is written as NOT(A) AND B and therefore the equation is (A AND NOT(B)) OR (NOT(A) AND B) which possibly simplifies to A XOR B
Calculation from the output values 0 of the truth table ( Maxterms ): for each 0 , write the corresponding input values separated by logical OR , then group these results with a logical AND .
Example: Rows 1 and 4 are equal to 0 , row 1 is written as A OR B , row 4 is written as NOT(A) OR NOT(B) and therefore the equation is (A OR B) AND (NOT(A) OR NOT(B)) which possibly simplifies to A XOR B
- What is the truth table for logical AND?
| A | B | A AND B |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
- What is the truth table for logical OR?
| A | B | A OR B |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
- What is the truth table for logical XOR?
| A | B | A B |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
- What is the truth table for logical NAND?
| A | B | A NAND B |
|---|---|---|
| 0 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
- What is the truth table for logical NOR?
| A | B | A NOR B |
|---|---|---|
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 0 |
- What is the truth table for logical TRUE?
| A | TRUE |
|---|---|
| 0 | 1 |
| 1 | 1 |
- What is the truth table for logical FALSE?
| A | FALSE |
|---|---|
| 0 | 0 |
| 1 | 0 |
- What are the minterms?
Minterms $ m $ are the sum of row numbers of the table which have a logical 1 output (row numbering from 0).
Example: $ X = a \oplus b $ ( XOR ) the truth table has 2 TRUE outputs at 2nd row (indexed 1) and 3rd row (indexed 2), so $ X = \sum{m(1,2)} $
- What are the maxterms?
Maxterms $ M $ are the product of row numbers of the table which have a logical 0 output (row numbering from 0).
Example: $ X = a \oplus b $ ( XOR ) the truth table has 2 outputs FALSE at the first and last lines denoted 0, and 3 therefore $ X = \prod{M(0,3)} $
Source code
dCode retains ownership of the "Truth Table" source code. Except explicit open source licence (indicated Creative Commons / free), the "Truth Table" algorithm, the applet or snippet (converter, solver, encryption / decryption, encoding / decoding, ciphering / deciphering, breaker, translator), or the "Truth Table" functions (calculate, convert, solve, decrypt / encrypt, decipher / cipher, decode / encode, translate) written in any informatic language (Python, Java, PHP, C#, Javascript, Matlab, etc.) and all data download, script, or API access for "Truth Table" are not public, same for offline use on PC, mobile, tablet, iPhone or Android app! Reminder : dCode is free to use.
The copy-paste of the page "Truth Table" or any of its results, is allowed (even for commercial purposes) as long as you credit dCode! Exporting results as a .csv or .txt file is free by clicking on the export icon Cite as source (bibliography): Truth Table on dCode.fr [online website], retrieved on 2024-08-15, https://www.dcode.fr/boolean-truth-table
Need Help ?
Questions / comments.
- Boolean Expressions Calculator
- Boolean Minterms and Maxterms
- Boolean Dual
- Decabit Code
- Capacitor Color Code
- 7-Segment Display
- DCODE'S TOOLS Only output values (list of 0 and 1)
- About dCode
Truth Table Generator
This tool generates truth tables for propositional logic formulas. You can enter logical operators in several different formats. For example, the propositional formula p ∧ q → ¬r could be written as p /\ q -> ~r , as p and q => not r , or as p && q -> !r . The connectives ⊤ and ⊥ can be entered as T and F .
Truth Table Generator
The logic tool to create truth table online.
Enter a logic expression
How to use ?
- Write your logical expression in the search box
- Use letters for variables, symbols for logical operators
| Operator | Symbol to type | Example |
|---|---|---|
| OR | A B C | |
| AND | A B C | |
| NOT | A | |
| NAND (AND + NOT) | (* *) | (A B C) |
| NOR (OR + NOT) | (* *) | (A B C) |
| XOR | A B |
- Click on the "Get Truth Table" button
- Truth Table will be displayed
- Click on the "Advanced Truth Table" button for propositional logic operations
Truth Table
Logic gate symbols.
- AND (symbolically: &)
- OR (symbolically: +)
- NOT (symbolically: !)
- NOR (Representing: Not – OR)
- NAND (Representing: Not - AND)
Truth Table Examples
Or gate truth table.
| Symbol | A | B | A+B |
|---|---|---|---|
| 0 | 0 | 0 | |
| 0 | 1 | 1 | |
| 0 | 1 | 1 | |
| 1 | 1 | 1 |
AND Gate Truth Table
| Symbol | A | B | AB |
|---|---|---|---|
| 0 | 0 | 0 | |
| 0 | 1 | 0 | |
| 1 | 0 | 0 | |
| 1 | 1 | 1 |
NAND Gate Truth Table
| Symbol | A | B | !(A.B) |
|---|---|---|---|
| 0 | 0 | 1 | |
| 0 | 1 | 1 | |
| 1 | 0 | 1 | |
| 1 | 1 | 0 |
NOR Gate Truth Table
| Symbol | A | B | !(A+B) |
|---|---|---|---|
| 0 | 0 | 1 | |
| 0 | 1 | 0 | |
| 1 | 0 | 0 | |
| 1 | 1 | 0 |
NOT Gate Truth Table
| Symbol | A | !A |
|---|---|---|
| 0 | 1 | |
| 1 | 0 |
Truth Table is a mathematical table and the base for all computing needs. It is used to find out if a propositional expression is true for all legitimate input values. Creating a Truth table involves a simple logic yet sometimes it may slow you down, especially when you are working on a last minute project. This is when you can make use of Truth Table Generator. Truth Table Generator is an online tool that is used to create logical truth tables instantly. You can enter logical operators in different formats and get accurate results as boolean logic symbols.
Advanced Truth Table
This tool generates truth tables for propositional logic formulas. You can enter logical operators in several different formats. For example, the propositional formula p ∧ q → ¬r could be written as p /\ q -> ~r , as p and q => not r , or as p && q -> !r . The connectives ⊤ and ⊥ can be entered as T and F .
What do you mean by Truth table?
What is the need of truth table, is 0 true or false.
Logic Calculator: Truth Tables
(featuring a purple monster and a psychic duck)
Introduction
This truth-table calculator for classical logic shows, well, truth-tables for propositions of classical logic. Featuring a purple munster and a duck, and optionally showing intermediate results, it is one of the better instances of its kind.
Use the buttons below (or your keyboard) to enter a proposition, then gently touch the duck to have it calculate the truth-table for you. Each time you touch the friendly monster to the duck's left, it will eat up a character (or, if there is selected text, the whole selection). If you double-click the monster, it will eat up the whole input (yum!).
Once the table is there, use the button "Show intermediate results" or "Hide intermediate results" to show or hide intermediate results in the table.
Since 2021 you may enter more than one proposition at a time, separating them with commas (e.g. " P∧Q, P∨Q, P→Q"). This makes it easier e.g. to compare propositions and to check if an argument is semantically valid.
See a few examples below. Clicking on an example will copy it to the input field. Alternatively, you may leave the input field completely empty. On touching the duck, its psychic personality will find out what proposition you are thinking of (this is an experimental feature).
(P→Q) — (P∧Q) — (P∨Q) — (P⊽Q) — (P↮Q) — (P∨¬P) — (P∧¬P) — (P→((Q→R)∧(¬S∨R))) — (P→Q)∨(Q→R) ((P ⊼ Q) ⊽ (P ⊼ Q))
If you prefer using your keyboard, you may use the strings "&" or "&&" to denote "∧"; the strings "|" or "||" to denote "∨"; the strings "=>" or "->" to denote "→"; the string "<=>" or "<->" to denote "↔"; and the strings "!" or "~" to denote "¬".
The tables are calculated in your browser, so the calculator is available offline, and the government won't ever find out what propositions you are working with (unless it hacks your computer).
Proposition
~!,]+" style="width:97%;">
No errors so far.
Truth Table
Show intermediate results
You haven't entered a proposition yet.

Operating the Logic server currently costs about 113.88€ per year (virtual server 85.07€, domain fee 28.80€); hence the Paypal donation link.
Boolean Algebra Solver
This may take awhile....
The website is currently getting the required resources.
If it takes longer than 30 seconds then please refresh unless you have slow internet.
Want to practice or learn SQL/Python?
Try out my other sites. https://www.sql-practice.com/ https://python-practice.com/
Solve practice questions using an online terminal.
Relations between Propositions: Consistency, Entailment, and Equivalence
Logical consistency.
Two or more propositions are logically consistent if it is possible for them to all be true at the same time. If there is no way for them all to be true at once, they are inconsistent . Inconsistent propositions are said to contradict one another.
To determine whether propositions are consistent or inconsistent, we can use either a truth table or the truth assignment method:
| A | B | (A ⊃ B) | (A ∨ B) | ~A |
|---|---|---|---|---|
| 0 | 0 | 1 | 0 | 1 |
| 0 | 1 | |||
| 1 | 0 | 0 | 1 | 0 |
| 1 | 1 | 1 | 1 | 0 |
| A | B | (A • B) | (~A ∨ ~B) |
|---|---|---|---|
| 0 | 0 | 0 | 1 |
| 0 | 1 | 0 | 1 |
| 1 | 0 | 0 | 1 |
| 1 | 1 | 1 | 0 |
- Truth assignment test for consistency: Assign “1” to the main connective of each proposition, then calculate the truth values of any other connectives and sentence letters that can be determined based on that assumption. If some letters cannot be calculated, try all possible combinations of values for those letters. If there is a way to assign truth values to the letters while keeping all of the propositions true, the propositions are consistent. Otherwise, they are inconsistent.

Logical Entailment
One proposition logically entails another if (and only if) there is no way for the former to be true while the latter is false.
| A | B | (A ≡ B) | (A • B) |
|---|---|---|---|
| 0 | 0 | ||
| 0 | 1 | 0 | 0 |
| 1 | 0 | 0 | 0 |
| 1 | 1 | 1 | 1 |
Thus, (A • B) entails (A ≡ B), but not vice versa .
- Truth assignment test for entailment: To determine whether one proposition entails another, assign “1 ” to the first proposition and assign “0” to the second proposition. Then calculate the truth values of any other connectives and sentence letters that can be determined based on that assumption. If some letters cannot be calculated, try all possible combinations of values for those letters. If there is a way to assign truth values to all the letters while keeping the first proposition true and the second false, then the first proposition doesn’t entail the second. On the other hand, if you can’t assign truth values to everything while keeping the first proposition true and the second false, then the first does entail the second.
Similarly, a set of propositions entails another set if (and only if) it is impossible for all the propositions in the first set to be true while any one of the propositions in the second set is false.
| A | B | (A ∨ B) | (A ⊃ B) | (B ⊃ A) | (A • B) | (A ≡ B) |
|---|---|---|---|---|---|---|
| 0 | 0 | 0 | 1 | 1 | 0 | 1 |
| 0 | 1 | 1 | 1 | 0 | 0 | 0 |
| 1 | 0 | 1 | 0 | 1 | 0 | 0 |
| 1 | 1 |
Logical Equivalence
| A | B | ~(A • B) | (~A ∨ ~B) |
|---|---|---|---|
| 0 | 0 | 1 | 1 |
| 0 | 1 | 1 | 1 |
| 1 | 0 | 1 | 1 |
| 1 | 1 | 0 | 0 |
- Truth assignment test for equivalence: First use the truth assignment test described above to determine whether the first proposition entails the second; then test whether the second entails the first. The two propositions are equivalent if (and only if) they entail each other.
PHIL102: Introduction to Critical Thinking and Logic
Truth Tables
Read these sections to learn how to interpret, make, and apply truth tables to sentential logic formulas, note conditional statements in sentential logic, and translate the word "unless" into sentential logic. Be sure to note the difference between an antecedent and a consequent and between a necessary and sufficient condition.
Complete the exercises, checking your answers against the key.
The truth table test of validity
So far, we have learned how to translate certain English sentences into our symbolic language, which consists of a set of constants (i.e., the capital letters that we use to represent different atomic propositions) and the truth-functional connectives. But what is the payoff of doing so? In this section we will learn what the payoff is. In short, the payoff will be that we will have a purely formal method of determining the validity of a certain class of arguments - namely, those arguments whose validity depends on the functioning of the truth- functional connectives. This is what logicians call "propositional logic" or "sentential logic".
In the first chapter, we learned the informal test of validity, which required us to try to imagine a scenario in which the premises of the argument were true and yet the conclusion false. We saw that if we can imagine such a scenario, then the argument is invalid. On the other hand, if it is not possible to imagine a scenario in which the premises are true and yet the conclusion is false, then the argument is valid. Consider this argument:
- The convict escaped either by crawling through the sewage pipes or by hiding out in the back of the delivery truck.
- But the convict did not escape by crawling through the sewage pipes.
- Therefore, the convict escaped by hiding out in the back of the delivery truck.
Using the informal test of validity, we can see that if we imagine that the first premise and the second premise are true, then the conclusion must follow. However, we can also prove this argument is valid without having to imagine scenarios and ask whether the conclusion would be true in those scenarios. We can do this by a) translating this sentence into our symbolic language and then b) using a truth table to determine whether the argument is valid. Let's start with the translation. The first premise contains two atomic propositions. Here are the propositions and the constants that I'll use to stand for them:
S = The convict escaped through the sewage pipes
D = The convict escaped by hiding out in the back of the delivery van
As we can see, the first premise is a disjunction and so, using the constants indicated above, we can translate that first premise as follows:
The second premise is simply the negation of S:
Finally, the conclusion is simply the atomic sentence, D. Putting this all together in standard form, we have:
We will use the symbol "∴" to denote a conclusion and will read it "therefore".
The next thing we have to do is to construct a truth table. We have already seen some examples of truth tables when I defined the truth-functional connectives that I have introduced so far (conjunction, disjunction, and negation). A truth table (as we saw in section 2.2) is simply a device we use to represent how the truth value of a complex proposition depends on the truth of the propositions that compose it in every possible scenario. When constructing a truth table, the first thing to ask is how many atomic propositions need to be represented in the truth table. In this case, the answer is "two," since there are only two atomic propositions contained in this argument (namely, S and D). Given that there are only two atomic propositions, our truth table will contain only four rows - one row for each possible scenario. There will be one row in which both S and D are true, one row in which both S and D are false, one row in which S is true and D is false, and one row in which S is false and D is true.
| D | S | S v D | ~S | D |
|---|---|---|---|---|
| T | T | |||
| T | F | |||
| F | T | |||
| F | F |
The two furthest left columns are what we call the reference columns of the truth table. Reference columns assign every possible arrangement of truth values to the atomic propositions of the argument (in this case, just D and S). The reference columns capture every logically possible scenario. By doing so, we can replace having to use your imagination to imagine different scenarios (as in the informal test of validity) with a mechanical procedure that doesn't require us to imagine or even think very much at all. Thus, you can think of each row of the truth table as specifying one of the possible scenarios. That is, each row is one of the possible assignments of truth values to the atomic propositions. For example, row 1 of the truth table (the first row after the header row) is a scenario in which it is true that the convict escaped by hiding out in the back of the delivery van, and is also true that the convict escaped by crawling through the sewage pipes. In contrast, row 4 is a scenario in which the convict did neither of these things.
The next thing we need to do is figure out what the truth values of the premises and conclusion are for each row of the truth table. We are able to determine what those truth values are because we understand how the truth value of the compound proposition depends on the truth value of the atomic propositions. Given the meanings of the truth functional connectives (discussed in previous sections), we can fill out our truth table like this:
| D | S | S v D | ~S | D |
|---|---|---|---|---|
| T | T | T | F | T |
| T | F | T | T | T |
| F | T | T | F | F |
| F | F | F | T | F |
To determine the truth values for the first premise of the argument ("S v D") we just have to know the truth values of S and D and the meaning of the truth functional connective, the disjunction. The truth table for the disjunction says that a disjunction is true as long as at least one of its disjuncts is true. Thus, every row under the "S v D" column should be true, except for the last row since on the last row both D and S are false (whereas in the first three rows at least one or the other is true). The truth values for the second premise (~S) are easy to determine: we simply look at what we have assigned to "S" in our reference column and then we negate those truth values - the Ts becomes Fs and the Fs becomes Ts. That is just what I've done in the fourth column of the truth table above. Finally, the conclusion in the last column of the truth table will simply repeat what we have assigned to "D" in our reference column, since the last conclusion simply repeats the atomic proposition "D".
The above truth table is complete. Now the question is: How do we use this completed truth table to determine whether or not the argument is valid? In order to do so, we must apply what I'll call the "truth table test of validity". According to the truth table test of validity , an argument is valid if and only if for every assignment of truth values to the atomic propositions, if the premises are true then the conclusion is true. An argument is invalid if there exists an assignment of truth values to the atomic propositions on which the premises are true and yet the conclusion is false. It is imperative that you understand (and not simply memorize) what these definitions mean. You should see that these definitions of validity and invalidity have a similar structure to the informal definitions of validity and invalidity (discussed in chapter 1). The similarity is that we are looking for the possibility that the premises are true and yet the conclusion is false. If this is possible, then the argument is invalid; if it isn't possible, then the argument is valid. The difference, as I've noted above, is that with the truth table test of validity, we replace having to use your imagination with a mechanical procedure of assigning truth values to atomic propositions and then determining the truth values of the premises and conclusion for each of those assignments.
Applying these definitions to the above truth table, we can see that the argument is valid because there is no assignment of truth values to the atomic propositions (i.e., no row of our truth table) on which all the premises are true and yet the conclusion is false. Look at the first row. Is that a row in which all the premises are true and yet the conclusion false? No, it isn't, because not all the premises are true in that row. In particular, "~S" is false in that row. Look at the second row. Is that a row in which all the premises are true and yet the conclusion false? No, it isn't; although both premises are true in that row, the conclusion is also true in that row. Now consider the third row. Is that a row in which all the premises are true and yet the conclusion false? No, because it isn't a row in which both the premises are true. Finally, consider the last row. Is that a row in which all the premises are true and yet the conclusion false? Again, the answer is "no" because the premises aren't both true in that row. Thus, we can see that there is no row of the truth table in which the premises are all true and yet the conclusion is false. And that means the argument is valid.
Since the truth table test of validity is a formal method of evaluating an argument's validity, we can determine whether an argument is valid just in virtue of its form, without even knowing what the argument is about! Here is an example:
- (A v B) v C
Here is an argument written in our symbolic language. I don't know what A, B, and C mean (i.e., what atomic propositions they stand for), but it doesn't matter because we can determine whether the argument is valid without having to know what A, B, and C mean. A, B, and C could be any atomic propositions whatsoever. If this argument form is invalid then whatever meaning we give to A, B, and C, the argument will always be invalid. On the other hand, if this argument form is valid, then whatever meaning we give to A, B, and C, the argument will always be valid.
The first thing to recognize about this argument is that there are three atomic propositions, A, B, and C. And that means our truth table will have 8 rows instead of only 4 rows like our last truth table. The reason we need 8 rows is that it takes twice as many rows to represent every logically possible scenario when we are working with three different propositions. Here is a simple formula that you can use to determine how many rows your truth table needs:
2 n (where n is the number of atomic propositions)
You read this formula "two to the n-th power". So if you have one atomic proposition (as in the truth table for negation), your truth table will have only two rows. If you have two atomic propositions, it will have four rows. If you have three atomic propositions, it will have 8 rows. The number of rows needed grows exponentially as the number of atomic propositions grows linearly. The table below represents the same relationship that the above formula does:
| Number of atomic propositions | Number of rows in the truth table |
|---|---|
| 1 | 2 |
| 2 | 4 |
| 3 | 8 |
| 4 | 16 |
| 5 | 32 |
So, our truth table for the above argument needs to have 8 rows. Here is how that truth table looks:
| A | B | C | (A v B) v C | ~A | C |
|---|---|---|---|---|---|
| T | T | T | |||
| T | T | F | |||
| T | F | T | |||
| T | F | F | |||
| F | T | T | |||
| F | T | F | |||
| F | F | T | |||
| F | F | F |
Here is an important point to note about setting up a truth table. You need to make sure that your reference columns capture each distinct possible assignment of truth values. One way to make sure you do this is by following the same pattern each time you construct a truth table. There is no one right way of doing this, but here is how I do it (and recommend that you do it too). Construct the reference columns so that the atomic propositions are arranged alphabetically, from left to right. Then on the right-most reference column (the C column above), alternate true and false each row, all the way to the bottom. On the reference column to the left of that (the B column above), alternate two rows true, two rows false, all the way to the bottom. On the next column to the left (the A column above), alternate 4 true, 4 false, all the way to the bottom.
The next step is to determine the truth values of the premises and conclusion. Note that our first premise is a more complex sentence that consists of two disjunctions. The main operator is the second disjunction since the two main grouping, denoted by the parentheses, are "A v B" and "C". Notice, however, that we cannot figure out the truth values of the main operator of the sentence until we figure out the truth values of the left disjunct, "A v B". So that is where we need to start. Thus, in the truth table below, I have filled out the truth values directly underneath the "A v B" part of the sentence by using the truth values I have assigned to A and B in the reference columns. As you can see in the truth table below, each line is true except for the last two lines, which are false, since a disjunction is only false when both of the disjuncts are false. (If you need to review the truth table for disjunction, please see section 2.3).
| A | B | C | (A v B) v C | ~A | C |
|---|---|---|---|---|---|
| T | T | T | T | ||
| T | T | F | T | ||
| T | F | T | T | ||
| T | F | F | T | ||
| F | T | T | T | ||
| F | T | F | T | ||
| F | F | T | F | ||
| F | F | F | F |
Now, since we have figured out the truth values of the left disjunct, we can figure out the truth values under the main operator (which I have emphasized in bold in the truth table below). The two columns you are looking at to determine the truth values of the main operator are the "A v B" column that we have just figured out above and the "C" reference column to the left. It is imperative to understand that the truth values under the "A v B" are irrelevant once we have figured out the truth values under the main operator of the sentence. That column was only a means to an end (the end of determining the main operator) and so I have grayed those out to emphasize that we are no longer paying any attention to them. (When you are constructing your own truth tables, you may even want to erase these subsidiary columns once you've determined the truth values of the main operator of the sentence. Or you may simply want to circle the truth values under the main operator to distinguish them from the rest).
| A | B | C | (A v B) v C | ~A | C |
|---|---|---|---|---|---|
| T | T | T | T T | ||
| T | T | F | T T | ||
| T | F | T | T T | ||
| T | F | F | T T | ||
| F | T | T | T T | ||
| F | T | F | T T | ||
| F | F | T | F T | ||
| F | F | F | F F |
Finally, we will fill out the remaining two columns, which is very straightforward. All we have to do for the "~A" is negate the truth values that we have assigned to our "A" reference column. And all we have to do for the final column "C" is simply repeat verbatim the truth values that we have assigned to our reference column "C".
| A | B | C | (A v B) v C | ~A | C |
|---|---|---|---|---|---|
| T | T | T | T T | F | T |
| T | T | F | T T | F | F |
| T | F | T | T T | F | T |
| T | F | F | T T | F | F |
| F | T | T | T T | T | T |
| F | T | F | T T | T | F |
| F | F | T | F T | T | T |
| F | F | F | F F | T | F |
The above truth table is now complete. The next step is to apply the truth table test of validity in order to determine whether the argument is valid or invalid. Remember that what we're looking for is a row in which the premises are true and the conclusion is false. If we find such a row, the argument is invalid. If we do not find such a row, then the argument is valid. Applying this definition to the above truth table, we can see that the argument is invalid because of the 6th row of the table (which I have highlighted). Thus, the explanation of why this argument is invalid is that the sixth row of the table shows a scenario in which the premises are both true and yet the conclusion is false.

- Documentation
- Course Notes
- 2.1.1. Characterizing Truth Tables
- 2.1.2. Truth Tables as Proofs
- 2.2. Logika Truth Tables
- 2.3. The Strange Case of the Imply-gate
- 2.4.1. Equality
- 2.4.2. The Double Negative
- 2.4.3. Exclusive OR (XOR)
- 2.4.4. De Morgan’s Law
- 2.4.5. Implication Equivalences
- 2.5. Why it is called the “Top Level” operator
- 2.6. Knowledge Travels Along the Wires of A Circuit
2. Circuits and Truth Tables ¶
In this chapter, we review basic notions about gates and learn the relationship between circuits and assignment-based computer programs. This sets the stage for analyzing modern programs.
2.1. Gates and Truth Tables ¶
Here are the four basic gates:
P AND Q | P OR Q | NOT P | P IMPLY Q |
|
|
|
|
In the above drawings, the input wires are labelled with the names P and Q . The output that is computed is emitted from the rightmost wire which exits the gate. For these simple gates, it is possible to exhaustively test every permutation of potential inputs and summarize results in a table, called a truth table.
Let’s examine the AND gate. The AND gate emits a high voltage ( 1 ) exactly when high voltages are sensed at input wires P and Q ; otherwise low voltage ( 0 ) is emitted. The gate’s physical behavior is summarized by in the following table.:
For the remainder of this course, we will use T (read “true”) for 1 and F (read “false”) for 0 . This is because we will examine applications that go far beyond circuit theory and base-two arithmetic. Here are the truth tables for the AND, OR, NOT and IMPLY gates:
The capital letters P and Q are intended to be place holders, not variables strictly named P and Q. Their use avoids the verbose, “Right-hand Side Operand” and “Left-hand Side Operand”.
OR is sometimes called “inclusive or”, because as long as one of its inputs is true, then its output is true. This differs from common United States English usage. Generally in spoken and written English, “or” carries the exclusive connotation. If offered a choice of “coffee or tea,” it is understood that you may select one but not both. The logical “or” is admits the possibility of both. It is more accurately translated into the English language as “and/or”.
The meaning of the IMPLY gate will be covered latter in this chapter. It is included here so all the gate information is consolidated.
Gate | ASCII | Math | UNICODE |
AND | ∧ | ∧ |
|
OR | v | ∨ |
|
NOT | ~ | ¬ |
|
IMPLY | -> | ⇒ |
|
These notes will typically use the UNICODE notations.
We can also compose the gates to define new operations.

which we can work out in stages, like this:
We begin by writing the value of each set of inputs on the left, under their corresponding symbol on the right. Next we apply the operator (gate) with the highest precedence (covered in Logical Operator Precedence below). In our case the “()” make the AND ( ∧ ) symbol the highest.
A truth assignment is a unique permutation of the possible inputs for a system. For the ∧-gate, it is a 2-variable sequence. Considering the first row we see we have ” T ∧ T”–looking that up in the ∧-gate truth table we see the result is also “T”, and we record that under the “∧” symbol. We do the same thing all the other truth assignments.
After the initial transcribing of the truth values under their respective variables, we look up the truth-values in the gate tables, not the variables. Also observe that while ∧ is symmetric, i.e. “T F” == “F T” == “F” the IMPLY gate is not.
Now we look up the value under the “∧” symbol in the ¬ gate table. In the first row we see that the truth assignment for the first row, “T”, is “F” and record it under the “¬” symbol. Do this for every row and we are done.
2.1.1. Characterizing Truth Tables ¶
In our study of logic, it will be convenient to characterize logical formula with a description of their truth tables. If all truth assignments for a logical formula are True, the formula is said to be a tautology. The formula p ∨ ¬ p is a tautology. In the following example, the * marks the top level or last evaluated operator.
A formula for which every truth assignment is False is called contradictory. The formula p ∧ ¬ p is contradictory (or a contradiction).
A formula for which some truth assignments are False and other’s True is called contingent. The equation p q | ¬ (q ∧ q) , from above is contingent.
1 * 2 --------------- 3 p q | ¬ (p ∧ q) 4 --------------- 5 T T | F T T T 6 T F | T T F F 7 F T | T F F T 8 F F | T F F F 9 --------------- 10 Contingent 11 - T : [T F] [F T] [F F] 12 - F : [T T]
In this section, we have used Logika truth tables. They are explained in more detail below. In this class, if you produce a truth table as part of an answer, it must match the Logika syntax.
2.1.2. Truth Tables as Proofs ¶
This is a class about logic. As such, much the class will involve formally proving some claim is always true, never true, or true only under certain conditions. Many types of “computing” problems can be expressed as truth tables.
Consider the simple 2-bit integer adder.
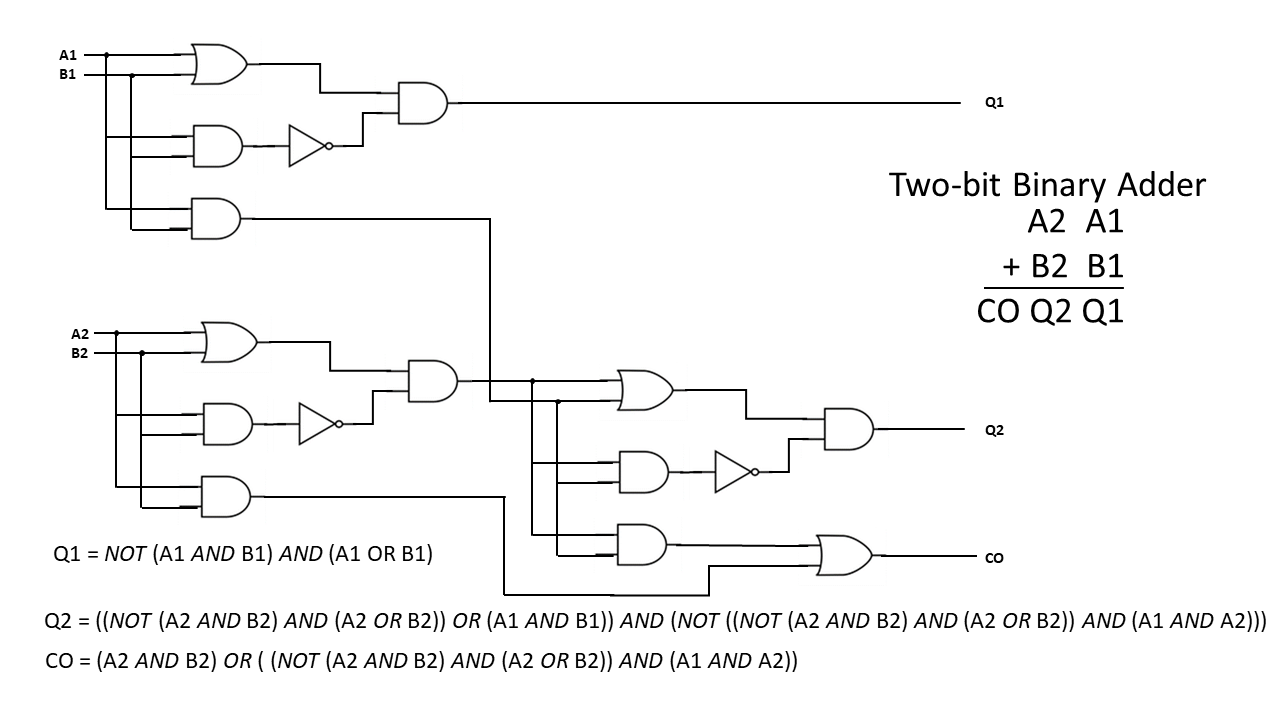
While it has a lot of parts (three “answer” tables, each with 2^2 truth assignments), it is certainly feasible (although irritating) to calculate these tables by hand. But recall, that most integers are represented by 32-bits, leading to 33 tables (don’t forget the Carry-Over or Overflow bit), each with 2^32 entries. This will take a bit (pun intended) over a 1,100-years to write out by hand if you can average one truth assignment per second.
Considering you will probably never be asked to write a real-world application as simple as integer addition, it is easy to conclude that it is infeasible to prove the correctness of programs by truth tables. The inability to test a program by exhaustively testing every input or state is known as the combinatorial explosion problem.
OKay … then why are we making you learn truth tables? Well, even when more advanced techniques are applied to prove logical statements, underling the techniques’ soundness are these primitive rules which are easily expressed and learned via truth tables.
2.2. Logika Truth Tables ¶
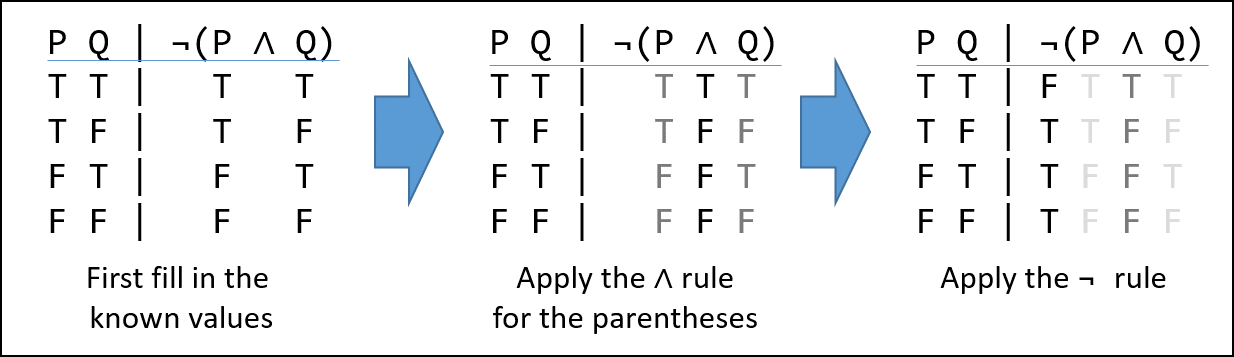
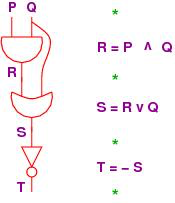
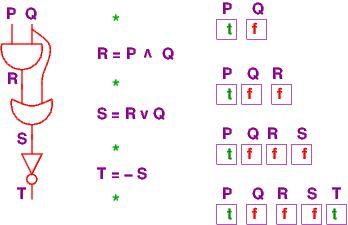
From this point forward, the course will expect you to use Logika formatted truth tables. The Logika truth table for the formula ¬ (P ∧ Q) is:
Logika truth tables have standard format (syntax) and semantic meanings. All elements of the truth table must be included to be considered correct.

The first line will always contain a single asterisk ( * ) over the last operator evaluated in the formula. This may also be referred to as the “top level” or “lowest precedent” operator. Why it is called the “top level” operator will be covered towards the end of this chapter.
Next is a line of - (minus sign) characters, these lines must be at least as long as the third line to avoid getting errors.
The third line contains “variables | formula”. As Logika uses some capital letters as reserved words, lower case letters are used as variable names. Additionally, variables should be listed alphabetically.
The fourth line is another row of - .
Next come the truth assignments. Convention is to start with all True and progress linearly to all False. Capital T and F must be used. In a truth assignment each variable is mapped to either true or false.
After the Truth assignments is another row of - .
Lastly comes the table. When all truth assignment cause the formula to be true, the word Tautology is used without an accompanying table. Similarly, when all truth assignments are false, Contradictory is used. All other results are Contingent , see the example in the figure above.
The order of precedence for logical operators from highest to lowest are:
Parentheses alter the order of operations as they do in normal algebra. Parenthetical expressions are evaluated from most-deeply nested to least-deeply nested (inside-to-outside).
2.3. The Strange Case of the Imply-gate ¶
The astute reader will notice that → truth tables work very different from ∧ and ∨ . To begin with, ∧ and ∨ truth assignments are symmetric; if [T F] == F then [F T] == F. This is not true of implication because, p → q is a composite claim that asserts that p holds knowledge sufficient to deduce q.
Lets use a concrete example from K-State. If I know you are majoring in computer science (fact p), then I know you are majoring in engineering (fact q).
However the converse, majoring in Engineering → majoring in Computer Science is not necessarily true.
Some students tend to conflate “p holds knowledge sufficient to deduce q” to mean “p == q”, and are surprised and indignant that the truth assignment [F T] in the IMPLY gate is True. p → q does not mean p == q or q == p
In the truth table for p → q , the result reflects the existence of a serial link between p and q . First p must be true, then q must also be true in order for the implication to be true.
If both are true, the link is true, and the implication (the relationship) between p and q is true.
If p is true and q is false, clearly p does not hold knowledge sufficient to deduce q, so the relationship is not true (false).
Finally, if p is not true, there is no way to know whether the relationship holds. In this case, the implication is said to be true, or vacuously true. There is certainly no evidence to prove that it is false.
Implication in logic was formalized by William of Ockham, in his book Summa Logicae in the 14th century. These somewhat convoluted rules add tremendous expressive power to logic and computation. Without them there would be no branching in programs (no IFs, no FORs, no WHILEs).
2.4. Common Logical Formula (circuit) Equivalences ¶
2.4.1. equality ¶.
Two (or more) logical statements are said to be equal IFF (if and only if, ↔ ) they have the same truth value for every truth assignment; i.e. their truth tables evaluate exactly the same. An example of equal are q ∧ p and p ∧ (q ∧ p)
Finding equivalent logical statements of fewer gates (states) is important to several fields. In computer science, fewer states can lead to less memory, fewer operations and smaller programs. In computer engineering, fewer gates means fewer circuits less power and less heat.
More technically, bi-implication is another way to express quality. However, we have not yet introduced an “equals” operator.
p = q ↔ (p → q) ∧ (q → p)
2.4.2. The Double Negative ¶
In Logika, and in many logic applications, double negations effectively cancel each other out. This is not the only possible interpretation of ¬ ¬ p , but it is the one implemented in Logika. We may discuss other interpretations in the section on Propositional Logic.
2.4.3. Exclusive OR (XOR) ¶
As previously discussed, common English usage of “or” is in the exclusive sense. (p XOR q) can be expressed in several ways:
In class, we will not accept the use of an XOR operator, you must express the all formula in terms of AND, OR, NOT and IMPLY.
2.4.4. De Morgan’s Law ¶
De Morgan’s Law is a statement about the relationship between AND and NOT-OR (NOR) ( ¬ ( p ∨ q) ). Specifically:
p ∧ q ↔ ¬ ( ¬ p ∨ ¬ q) p ∨ q ↔ ¬ ( ¬ p ∧ ¬ q)
This has important implications for computer engineering, allowing all logic constructions to be expressed with only two types of basic gates, NAND and NOT; greatly economizing integrated chip production.
Augustus De Morgan also coined the term Mathematical Induction and provided a rigorous approach for its proof. Mathematical induction is the basis for many computer science proofs in areas of algorithms, languages and computational complexity.
2.4.5. Implication Equivalences ¶
Finally, implication can be expressed as negation and OR; or as its contra-positive statement.
(p → q) ↔ ¬ p ∨ q (p → q) ↔ ( ¬ q → ¬ p) the contrapositive statement
The converse of an implication may or may not be true
(p → q) ??? (q → p) the converse (NOT NECESSARILY AN EQUIVALENCE)
While most of the formula presented in this section are true equivalences, IF you are asked to prove they are equal by truth table, it is expected that you would make a truth table for each side of the ↔ and show that their values match for every truth assignment.
2.5. Why it is called the “Top Level” operator ¶
Let us return to the 2-bit adder, and consider only the circuitry for Q1. In a circuit, knowledge can be said to flow along the wires, where it is transformed by gates and the new knowledge propagates to the next point.
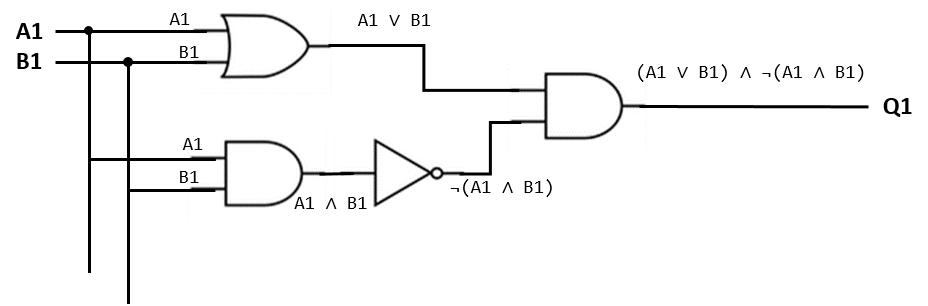
In the circuit annotated above, it is clear what knowledge (facts and deduced facts) flow in each wire segment. A common mathematical, hence computer science technique is to represent this type of knowledge flow in specialized type of graph called a tree. A tree is represented by a collection of nodes and edges, one node is selected as the “root” and all nodes have a unique path (a collection of edges) leading to the root node. By convention, the tree is drawn inverted, with its root at the top and its leaves hanging from the bottom.
In computer science, the root is selected to be the node which provides the “final answer” to the problem. As you can see, edges carry facts and nodes are operators which deduce new facts.
The tree representation of a computer program is a fundamental abstraction for computer scientist. Modern compilers and interpreters take a program written in a high level programing language and convert it into an abstract syntax tree (AST), which is then converted to machine-code. For languages in the functional paradigm (C# and Java are in the imperative and/or object paradigms ), there is a strong correlation between the high-level program’s structure and that of the AST.
When we compare the tree with the logical statement, we see the lowest priority operator is the root of the tree; hence the term “Top Level” operator.
2.6. Knowledge Travels Along the Wires of A Circuit ¶
So far, we pretended that low- and high-voltage levels travel along the wiring of a circuit. But it is really knowledge that travels the circuit. This is understood with some pictures. Here is a circuit:
and here is its coding in equations:
Let’s redraw the circuit vertically and lay it side by side with the assignment equations:
Each wire in the circuit is named. These are just variable names . Indeed, the first (electronic) computer programs, in the 1940s, were descriptions of wiring diagrams like this one. The modern stored-program computer, developed by John von Neumann in the 1950s, used storage registers to hold the values of the variable names and used a processor to compute the values of the equations. In this way, a processor-plus-registers can simulate a circuit, and all computer programs are merely descriptions of circuits in which information flows through the wires (the variables) .
This is the origin of variable-based, assignment-based computer programming. Now, at each of the program points , marked by stars in the above diagram, what information travels in the wires? We might use the circuit with some inputs to see “what happens”. Say that we supply true for P and false for Q :
The diagram shows the values on the wires labelled P , Q , R and S as they travel through the circuit. But this is just tracking the values of the variables in the assignment program we wrote! The “output variable”/write, named T , has value true .
Just as interesting is that we can analyze the program/circuit before it is completely tested. For example, say that the circuit will be inserted into a board where its P wire will always receive a t as input, but we don’t know what Q will receive. What can we predict about the circuit’s behavior once it is embedded in the board? It’s this:

In the diagram, we see that R = Q is stated after the AND gate. How do we know this? First, we do know that R = P ∧ Q . But P = true . We substitute true for P and obtain R = true ∧ Q . Next, we do a cases analysis and consider the cases of Q ’s possible value: If Q is true , then true ∧ Q is true ∧ true , which simplifies to true , that is, to Q ’s value. Similarly, when Q is false , then t ∧ Q is false as well. Hence, in both cases, true ∧ Q equals Q .
The above reasoning is a deduction – we deduced from the facts P = true and R = P ∧ Q that R = Q . The whole point of this course is to learn how to make such deductions.
The other deductions in the example are calculated with similar uses of substitution, simplification, and cases analysis.
The point of the previous example is that we can deduce (predict) properties of the circuit in advance of using it. These deductions complement testing.
Next, say that we don’t know anything about P and Q as inputs. What can be stated about the circuit’s output? Well, it’s this:
stating the obvious! But by a careful examination of the truth tables, we can also state that T = ¬Q . Later in the course, we learn deduction rules that calculate this result, not relying on truth tables.
Finally, we can make circuits that take three or more inputs, e.g., (¬(P ∧ Q)) ∨ R computes:
Here, the column underneath OR defines the output. We see this circuit emits false only when P and Q are both true and R is false. This is a hint that the circuit, ¬(P ∧ Q ∧ ~R) , behaves the same way (has the same truth table) as the one above. Yet another equivalent circuit is (¬P) ∨ (¬Q) ∨ R . (Why?)
In circuit design, finding equivalent circuits with fewer gates and variables saves power, time and material.
This note was adapted from David Schmidt's CIS 301, 2008, Chapter 0 course note.
It was updated in 2018 by Dr John Hatcliff and George Lavezzi to conform with Logika syntax and more closely match KSU's CIS 301 course as taught in Spring 2018.
Stack Exchange Network
Stack Exchange network consists of 183 Q&A communities including Stack Overflow , the largest, most trusted online community for developers to learn, share their knowledge, and build their careers.
Q&A for work
Connect and share knowledge within a single location that is structured and easy to search.
Using a truth table to test argument validity in predicate logic with finite domain.
I'm just making the transition from propositional logic to predicate logic and I was wondering how we would use truth tables to test the validity of an argument expressed in predicate logic.
Say, our universe of discourse comprises two smurfs named Clumsy and Hefty. I have the following argument:
Clumsy is a smurf. All smurfs are blue. Therefore, Clumsy is blue.
I translated this into predicate logic as follows:
$S(x)$ - "x is a smurf" $B(x)$ - "x is blue"
Premises: P1. $S(c)$ P2. $\forall x B(x)$ Conclusion: $∴ B(c)$
Assuming that I have expressed the argument correctly, let
- $S(c)$ - "Clumsy is a smurf"
- $S(h)$ - "Hefty is a smurf"
- $B(c)$ - "Clumsy is blue"
- $B(h)$ - "Hefty is blue"
Then I can make a truth table as follows (the table can be viewed/edited here ):

- Have I expressed the argument correctly?
- Is my truth table correct?
I wasn't quite sure how to check the premise "all smurfs are blue" in the truth table. I basically just broke the predicate $\forall x B(x)$ down into two statements (one for each smurf in the universe): $S(c) ⇒ B(c)$ and $S(h) ⇒ B(h)$ . Then to assess validity, I checked that the conclusion was true for all lines where $S(h)$ , $S(c) ⇒ B(c)$ and $S(h) ⇒ B(h)$ are all true. Since the conclusion is always true when all the premises are true (see highlighted rows), I concluded that the argument must be valid.
EDIT: On second thoughts, I think $\forall x B(x)$ should be $S(c) ⇒ B(c) \land S(h) ⇒ B(h)$ , but the highlighted rows would remain unchanged, so it wouldn't affect the conclusion that the argument is valid.
- propositional-calculus
- predicate-logic
- $\begingroup$ Caution: Just because a conclusion is a consequence of the premises doesn't mean an argument is valid, especially if the argument contains intermediate claims between them. $\endgroup$ – aschepler Commented Sep 16, 2022 at 23:45
- $\begingroup$ Thanks @aschepler, by "intermediate claims", do you mean $S(c)⇒B(c)$ and $S(h)⇒B(h)$? I really wasn't sure about these, so I wouldn't be surprised if they are incorrect. I just figured that saying $∀xB(x)$ is tantamount to requiring $S(x)⇒B(x)$ for all objects in our domain. $\endgroup$ – user51462 Commented Sep 17, 2022 at 0:06
- $\begingroup$ This argument has no intermediate claims, just premises and a conclusion. Yes, it's strange to use $\forall x B(x)$, which says "everything is blue". In that case, it doesn't matter what is or isn't a smurf: $\forall x B(x)$ as the only premise justifies $B(c)$. I'd write "all smurfs are blue" as $\forall x (S(x) \rightarrow B(x))$. (Though if the universe contains exactly the two objects $c$ and $h$, then yes, $(S(c) \rightarrow B(c)) \land (S(h) \rightarrow B(h))$ is equivalent.) $\endgroup$ – aschepler Commented Sep 17, 2022 at 0:27
- $\begingroup$ Is the purpose here to evaluate claims given a fixed universe of discourse, or to find an appropriate universe of discourse for examining the truth of a given claim? $\endgroup$ – aschepler Commented Sep 17, 2022 at 0:29
- 1 $\begingroup$ Just to clarify, by $\forall x B(x)$, I meant $\forall x \in U (B(x))$, where $U = \{Clumsy, Hefty\}$. $\endgroup$ – user51462 Commented Sep 17, 2022 at 0:44
2 Answers 2
Yes, assuming that the domain is finite, you can indeed use a truth table to check the validity of an argument involving a first-order statement (though even though you can, you probably SHOULDN'T do it; more on this towards the end of the answer).
The reason for this is that the universal quantifier is, essentially, just a big block of conjuctions. Saying e.g.
$\forall x\in\{6,3,8\}:P(x)$
is (by definition) the same as saying
$P(6)\land P(3)\land P(8)$
Essentially, the (finitely domained) first-order statement has now been decomposed into ordinary propositions, so naturally it is possible to use them in a truth table. That being said, you probably SHOULDN'T do it either way; the truth tables will become exponentially bigger and less intuitive as the domain expands. Instead, you should be using the laws of inference instead. They have the great benefits of being MUCH more intuitive, as well as also working on infinite domains.
In your example, a more intuitive way to prove the validity of the argument would be as follows;
First of all, we know (by the rule of inference) that
$\forall x(S(x)\implies B(x))$
$S(c)\implies B(c)$
Going back to the original problem, we have
$S(c) \land \forall x(S(x)\implies B(x))$
As discussed above, this implies
$S(c) \land (S(c)\implies B(c))$
Which obviously implies $B(c)$
If you want to make the proccess even easier to understand (though a bit longer, and limited to a finite domain), you can also just express the first-order statement as a block of conjuctions of propositions and go from there;
$S(c) \land \forall x\in\{c, h\}(S(x)\implies B(x))$
$\iff S(c) \land (S(c)\implies B(c)) \land (S(h)\implies B(h))$
$\implies(S(c) \land (S(c)\implies B(c)))$
$\implies B(c)$
I was wondering how we would use truth tables to test the validity of an argument expressed in predicate logic.
We wouldn't. You can not use truth tables in predicate logic.
The only case where this works is if the formula is merely a first-order instance of a propositional tautology, i.e. a formula that can be obtained by inserting predicate logic formulas for propositional variables in a propositionally valid formula. E.g. $\forall x P(x) \lor \neg \forall x P(x)$ , which is just an instance of $p \lor \neg p$ with $\forall x P(x)$ taking the place of $p$ .
But we can not look "inside" the atomic formulas and reason about how individuals and predicates relate to each other using this method. There just exists no such thing as truth tables for predicate logic.
- 1 $\begingroup$ Thanks @lemontree, but what if the domain were small, wouldn't we be able to enumerate all possible combinations of truth assignments for all objects in the domain (like I've done in the table in my post) and then evaluate validity just as we would in propositional logic? $\endgroup$ – user51462 Commented Sep 17, 2022 at 3:07
- $\begingroup$ Yes, as long as the domain is finite, we can technically do it. So your idea isn't all wrong, it's just that it doesn't generalize, and isn't standard practice. Dark Rebellion's answer explains it well. $\endgroup$ – Natalie Clarius Commented Sep 19, 2022 at 19:23
You must log in to answer this question.
Not the answer you're looking for browse other questions tagged logic propositional-calculus predicate-logic ..
- Upcoming Events
- 2024 Community Moderator Election ends in 7 days
- Featured on Meta
- We've made changes to our Terms of Service & Privacy Policy - July 2024
- Bringing clarity to status tag usage on meta sites
- Upcoming Moderator Election
- 2024 Community Moderator Election
Hot Network Questions
- Counter in Loop
- Why are these simple equations so slow to `Solve`?
- How to make a case based on factual evidence that my colleague's writing style for submitted manuscripts has got to be overhauled?
- Looking for a British childrens book, I think from the 1950s, called "C-for-Charlie"
- Erase the loops
- Why do individuals with revoked master’s/PhD degrees due to plagiarism or misconduct not return to retake them?
- How does Anchor know space needed for an ata when we don't provide space?
- How is delayed luggage returned to its owners from a location with infrequent flights?
- In "Take [action]. When you do, [effect]", is the action a cost or an instruction?
- Short story about a committee planning to eliminate 1 in 10 people
- If there is no free will, doesn't that provide a framework for an ethical model?
- When would it be legal to ask back (parts of) the salary?
- How much air escapes into space every day, and how long before it makes Earth air pressure too low for humans to breathe?
- can a CPU once removed retain information that poses a security concern?
- Why do instructions for various goods sold in EU nowadays lack pages in English?
- Is an invalid date considered the same as a NULL value?
- Rock paper scissor game in Javascript
- How to interpret coefficients of logistic regression using natural cubic splines?
- I submitted a paper and later realised one reference was missing, although I had written the authors in the body text. What could happen?
- Is there any point "clean-installing" on a brand-new MacBook?
- Automotive Controller LDO Failures
- A study on the speed of gravity
- WW2 Bombers continuing on one of 2 or 4 engines, how would that work?
- Would it be possible for humans to be alive to witness the beginning of a runaway greenhouse effect on Earth?
| C H A P T E R 4 |
| Direct Proofs |
4.1 Introduction
Checking logical entailment with truth tables has the merit of being conceptually simple. However, it is not always the most practical method. The number of truth assignments of a language grows exponentially with the number of logical constants. When the number of logical constants in a propositional language is large, it may be impossible to process its truth table.
Proof methods provide an alternative way of checking logical entailment that addresses this problem. In many cases, it is possible to create a proof of a conclusion from a set of premises that is much smaller than the truth table for the language; moreover, it is often possible to find such proofs with less work than is necessary to check the entire truth table.
We begin this lesson by defining some basic concepts - axiom schemas, rules of inference, and direct proofs. We then look at a couple of proof systems, with emphasis on one particular proof system, viz. the Hilbert system . After that, we look at the properties of soundness and completeness - the standards by which proof systems are judged. Finally, we look at hierarchical proofs and some meta-theorems about proofs.
4.2 Axiom Schemas
An axiom schema (or schema ) is an expression satisfying the grammatical rules of our language except for the occurrence of metavariables (written here as Greek letters) in place of various subparts of the expression. For example, the following expression is a schema with metavariables φ and ψ.
An instance of an axiom schema is the sentence obtained by consistently substituting sentences for the metavariables in the rule. For example, the following are all instances of the schema above.
| ⇒ ( ⇒ ) |
| ⇒ ( ⇒ ) |
| ¬ ⇒ ( ⇒ ¬ ) |
| ( ⇒ ) ⇒ (( ⇒ ) ⇒ ( ⇒ )) |
An axiom schema is valid if and only if every instance of the schema is valid. The schema above is valid, as are the schemas shown below.
| Reflexivity | φ ⇒ φ |
| Negation Elimination | ¬¬φ ⇒ φ |
| Negation Introduction | φ ⇒ ¬¬φ |
| Tautology | φ ∨ ¬φ |
In what follows, we use both non-valid and valid axiom schemas. Non-valid schemas play a role in defining rules of inference, and valid schemas are used as components of deductive proof systems.
4.3 Rules of Inference
A rule of inference is a pattern of reasoning consisting of some schemas, called premises , and one or more additional schemas, called conclusions . Rules of inference are often written as shown below. The schemas above the line are the premises, and the schemas below the line are the conclusions.
| φ ⇒ ψ | ||
| φ | ||
| ψ | ||
The rule in this case is called Implication Elimination (or IE), because it eliminates the implication from the first premise.
Implication Creation (IC), shown below, is another example. This rule tells us that, if a sentence ψ is true, we can infer (φ ⇒ ψ) for any φ whatsoever.
| ψ | ||
| φ ⇒ ψ | ||
Implication Distribution (ID) tells us that implication can be distributed over other implications. If (φ ⇒ (ψ ⇒ χ)) is true, then we can infer ((φ ⇒ ψ) ⇒ (φ ⇒ χ)).
| φ ⇒ (ψ ⇒ χ) | ||
| (φ ⇒ ψ) ⇒ (φ ⇒ χ) | ||
Implication Reversal (IR) allows us to infer an implication if we have an implication with the arguments reversed and negated. If we know (¬ψ ⇒ ¬φ), we can infer (φ ⇒ ψ).
| ¬ψ ⇒ ¬φ | ||
| φ ⇒ ψ | ||
An instance of a rule of inference is the rule obtained by consistently substituting sentences for the metavariables in the rule. For example, the following is an instance of Implication Elimination.
| ⇒ | ||
If a metavariable occurs more than once, the same expression must be used for every occurrence. For example, in the case of Implication Elimination, it would not be acceptable to replace one occurrence of φ with one expression and the other occurrence of φ with a different expression.
Note that the replacement can be an arbitrary expression so long as the result is a legal expression. For example, in the following instance of Implication Elimination, we have replaced the variables by compound sentences.
| ( ⇒ ) ⇒ ( ⇒ ) | ||
| ( ⇒ ) | ||
| ( ⇒ ) | ||
Remember that there are infinitely many sentences in our language. Even though we start with finitely many propositional constants (in a propositional vocabulary) and finitely many operators, we can combine them in arbitrarily many ways. The upshot is that there are infinitely many instances of any rule of inference involving metavariables.
A rule applies to a set of sentences if and only if there is an instance of the rule in which all of the premises are in the set. In this case, the conclusions of the instance are the results of the rule application.
For example, if we had a set of sentences containing the sentence p and the sentence ( p ⇒ q ), then we could apply Implication Elimination to derive q as a result. If we had a set of sentences containing the sentence ( p ⇒ q ) and the sentence ( p ⇒ q ) ⇒ ( q ⇒ r ), then we could apply Implication Elimination to derive ( q ⇒ r ) as a result.
In using rules of inference, it is important to remember that they apply only to top-level sentences, not to components of sentences. While applying to components sometimes works, it can also lead to incorrect results.
As an example of such a problem, consider the incorrect application of Implication Elimination shown below. Suppose we believe ( p ⇒ q ) and ( p ⇒ r ). We might try to apply Implication Elimination here, taking the first premise as the implication and taking the occurrence of p in the second premise as the matching condition, leading us to conclude ( q ⇒ r ).
| ⇒ | ||
| ⇒ | ||
| Wrong! | ⇒ | Wrong! |
Unfortunately, this is not a proper logical conclusion from the premises, as we all know from experience and as we can quickly determine by looking at the associated truth table. It is important to remember that rules of inference apply only to top-level sentences.
4.4 Direct Proofs
By writing down premises, writing instances of axiom schemas, and applying rules of inference, it is possible to derive conclusions that cannot be derived from the premises in a single step. This idea of stringing things together in this way leads to the notion of a direct proof.
A direct proof of a conclusion from a set of premises is a sequence of sentences terminating in the conclusion in which each item is either (1) a premise, (2) an instance of an axiom schema, or (3) the result of applying a rule of inference to earlier items in sequence.
Here is an example. Suppose we have the set of sentences we saw earlier. We start our proof by writing out our premises. We believe p ; we believe ( p ⇒ q ); and we believe that ( p ⇒ q ) ⇒ ( q ⇒ r ). Using Implication Elimination on the first premise and the second premise, we derive q . Applying Implication Elimination to the second premise and the third premise, we derive ( q ⇒ r ). Finally, we use the derived premises on lines 4 and 5 to arrive at our desired conclusion.
| 1. | Premise | |
| 2. | ⇒ | Premise |
| 3. | ( ⇒ ) ⇒ ( ⇒ ) | Premise |
| 4. | Implication Elimination: 2, 1 | |
| 5. | ⇒ | Implication Elimination: 3, 2 |
| 6. | Implication Elimination: 5, 4 |
Here is another example. Whenever p is true, q is true. Whenever q is true, r is true. With these as premises, we can prove that, whenever p is true, r is true. On line 3, we use Implication Creation to derive ( p ⇒ ( q ⇒ r )). On line 4, we use Implication Distribution to distribute the implication in line 3. Finally, on line 5, we use Implication Elimination to produce the desired result.
| 1. | ⇒ | Premise |
| 2. | ⇒ | Premise |
| 3. | ⇒ ( ⇒ ) | Implication Creation: 2 |
| 4. | ( ⇒ ) ⇒ ( ⇒ ) | Implication Distribution: 3 |
| 5. | ⇒ | Implication Elimination: 4, 1 |
Let R be a set of rules of inference. If there exists a proof of a sentence φ from a set Δ of premises using the rules of inference in R, we say that φ is provable from Δ using R. We usually write this as Δ ⊢ R φ, using the provability operator ⊢ (which is sometimes called single turnstile ). If the set of rules is clear from context, we usually drop the subscript, writing just Δ ⊢ φ.
4.5 Proof Systems
A proof system is a finite set of axiom schemata and rules of inference. Although it is interesting to consider proof systems with non-valid axiom schemata or unsound rules of inference, in this book we concentrate exclusively on proof systems with valid axiom schemata and sound rules of inference.
The Hilbert System is a well-known proof system for Propositional Logic. It has one rule of inference, viz. Implication Elimination.
In addition, the Hilbert systems has three axiom schemas. See below. These are the axiomatic versions of rules of inference we saw earlier. In the Hilbert system, each rule takes the form of an implication. The premises of each rule are written as antecedents of an implication and the rule's conclusion is written as the consequent of the implication.
| Implication Creation (IC) | φ ⇒ (ψ ⇒ φ) |
| Implication Distribution (ID) | (φ ⇒ (ψ ⇒ χ)) ⇒ ((φ ⇒ ψ) ⇒ (φ ⇒ χ)) |
| Implication Reversal (IR) | (¬ψ ⇒ ¬φ) ⇒ (φ ⇒ ψ) |
| 1. | ⇒ | Premise |
| 2. | ⇒ | Premise |
| 3. | ( ⇒ ) ⇒ ( ⇒ ( ⇒ )) | Implication Creation |
| 4. | ⇒ ( ⇒ ) | Implication Elimination: 3, 2 |
| 5. | ( ⇒ ( ⇒ )) ⇒ (( ⇒ ) ⇒ ( ⇒ )) | Implication Distribution |
| 6. | ( ⇒ ) ⇒ ( ⇒ ) | Implication Elimination: 5, 4 |
| 7. | ⇒ | Implication Elimination: 6, 1 |
The Hilbert System is interesting in that is sufficient to prove all logical consequences from any set of premises expressed using only ¬ and ⇒. And, as we shall see later, this subset of sentences is interesting because, for every sentence in Propositional Logic, there is a logically equivalent sentence written in terms of just these two operators. Moreover, there is an inexpensive algorithm for converting every Propositional Logic sentence to its equivalent sentence in this form.
4.6 Soundness And Completeness
In talking about Logic, we now have two notions - logical entailment and provability. A set of premises logically entails a conclusion if and only if every truth assignment that satisfies the premises also satisfies the conclusion. A sentence is provable from a set of premises if and only if there is a finite proof of the conclusion from the premises.
The concepts are quite different. One is based on truth assignments; the other is based on symbolic manipulation of expressions. Yet, for the proof systems we have been examining, they are closely related.
We say that a proof system is sound if and only if every provable conclusion is logically entailed. In other words, if Δ ⊢ φ, then Δ ⊨ φ. We say that a proof system is complete if and only if every logical conclusion is provable. In other words, if Δ ⊨ φ, then Δ ⊢ φ.
The Hilbert system is sound and complete for Propositional Logic. In other words, for this system, logical entailment and provability are identical. An arbitrary set of sentences Δ logically entails an arbitrary sentence φ if and only if φ is provable from Δ using Hilbert.
The upshot of this result is significant. On large problems, the proof method often takes fewer steps than the truth table method. (Disclaimer: In the worst case, the proof method may take just as many or more steps to find an answer as the truth table method.) Moreover, proofs are usually much smaller than the corresponding truth tables. So writing an argument to convince others does not take as much space.
4.5 Practical Matters
An axiom schema is an expression satisfying the grammatical rules of our language except for the occurrence of metavariables in place of various subparts of the expression. An instance of a schema is the expression obtained by substituting expressions of the appropriate sort for the metavariables in the schema so that the result is a legal expression. A valid axiom schema is one for which all instances are valid sentences. A rule of inference is a pattern of reasoning consisting of a set of schemas, called premises , and a second set of schemas, called conclusions . A direct proof of a conclusion from a set of premises is a sequence of sentences terminating in the conclusion in which each item is either (1) a premise, (2) an instance of an axiom schema, or (2) the result of applying a rule of inference to earlier items in sequence. If there exists a proof of a sentence φ from a set Δ of premises and the axiom schemas and rules of inference of a proof system, then φ is said to be provable from Δ (written as Δ ⊢ φ) and is called a theorem of Δ. A proof system is a finite set of axiom schemata and rules of inference. A proof system is sound if and only if every provable conclusion is logically entailed. A proof system is complete if and only if every logical conclusion is provable. The Hilbert System is sound and complete for Propositional Logic.
Exercise 4.1: Given ( p ⇒ ( q ⇒ r )) and ( p ⇒ q ), use the Hilbert system to prove ( p ⇒ r ).
Exercise 4.2: Given ( q ⇒ r ), use the Hilbert system to prove (( p ⇒ q ) ⇒ ( p ⇒ r )).
Exercise 4.3: Given p and ¬ p , use the Hilbert system to prove q .
Exercise 4.4: Use the Hilbert system to prove ( p ⇒ p ). No premises needed since this sentence is valid.
Exercise 4.5: Given p and ¬ p , use the Hilbert system to prove (¬ p ⇒ ( p ⇒ q )). No premises needed since this sentence is valid.
[SL07] Validity
Module: Sentential logic
- SL01. Introduction
- SL02. Well-formed formula
- SL03. Connectives
- SL04. Complex truth-tables
- SL05. Properties & relations
- SL06. Formalization
- SL08. The indirect method
- SL09. Indirect method: exercises
- SL10. Material conditional
- SL11. Derivations
- SL12. Derivation rules 1
- SL13. Derivation rules 2
- SL14. List of derivation rules
- SL15. Derivation strategies
- SL16. Soundness
- SL17. Completeness
- SL18. Limitations
Quote of the page
- Albert Camus
Popular pages
- What is critical thinking?
- What is logic?
- Hardest logic puzzle ever
- Free miniguide
- What is an argument?
- Knights and knaves puzzles
- Logic puzzles
- What is a good argument?
- Improving critical thinking
- Analogical arguments
§1. The full truth-table method
In this tutorial we study how to make use of full truth-table method to check the validity of a sequent in SL. Consider this valid sequent:
P, (P→Q) ⊧ Q
To prove that it is valid, we draw a table where the top row contains all the different sentence letters in the argument, followed by the premises, and then the conclusion. Then, using the same method as in drawing complex truth-tables, we list all the possible assignments of truth-values to the sentence letters on the left. In our particular example, since there are only two sentence letters, there should be 4 assignments :
| P | Q | P | ( | P | → | Q | ) | Q | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| T | T | |||||||||||||
| T | F | |||||||||||||
| F | T | |||||||||||||
| F | F |
The next step is to draw the truth-table for all the premises and also the conclusion:
In the completed truth-table, the first two cells in each row give us the assignment of truth-values, and the next three cells tell us the truth-values of the premises and the conclusion under each of the assignment. If an argument is valid, then every assignment where the premises are all true is also an assignment where the conclusion is true. It so happens that there is only one assignment (the first row) where both premises are true. We can see from the last cell of the row that the conclusion is also true under such an assignment. So this argument has been shown to be valid.
In general, to determine validity, go through every row of the truth-table to find a row where ALL the premises are true AND the conclusion is false. Can you find such a row? If not, the argument is valid. If there is one or more rows, then the argument is not valid.
Note that in the table above the conclusion is false in the second and the forth row. Why don't they show that the argument is invalid? answer
§2. More examples
Remember that “(P→Q), ~P, therefore ~Q” is invalid. Look at the truth-table, and determine which line is supposed to show that? answer
To show that a sequent is invalid, we find one or more assignment where all the premises are true and the conclusion is false. Such an assignment is known as an invalidating assignment (a counterexample) for the sequent.
Let's look at a slightly more complex sequent and draw the truth-table:
(~P∨Q), ~(Q→P) ⊧ (Q↔~P)
Again we draw a truth-table for the premises and the conclusion :
To help us calculate the truth-values of the WFFs under each assignment, we use the full truth-table method to write down the truth-values of the sentence letters first, and then work out the truth-values of the whole WFFs step by step. The truth-values of the complete WFFs under each assignment is written beneath the main operator of the WFFs. As you can see, the critical one to check is the third assignment. Since there is no assignment where the premises are true and the conclusion is false, the sequent is valid.
Examine this table and answer the questions:
True or false?
Use the full truth-table method to determine the validity of these sequents:
- ((P→Q)&R), (~Q∨R) ⊧ (P↔(Q↔R))
- (((P&Q)&~S) & (~Q↔R)), ~(~R→S) ⊧ ((P→Q)→(S→R))
See this page for the answers.
Confirm for yourself that the WFFs in each pair of WFFs below are logically equivalent to each other :
- (P→Q), (~Q→~P)
- (P↔Q), (~P↔~Q)
- ~(PvQ), (~P&~Q)
- ~(P&Q), (~Pv~Q)
§3. Some informal comments on decidability
One thing you might notice about the full truth-table method is that it can help us determine the validity of any sequent in SL. A program can be written that, given any finite sequent in SL as input, after a finite number of processing steps, produces an output "Yes" if the sequent is valid, or an output "No" if it is not. Of course, the computer would need to have a lot of memory if the sequent is a long one, but in principle it can be done. This is roughly what logicians mean when they say that validity in SL is decidable . Intuitively, it is a matter of whether there is an algorithm or computer program that can come up with a proof of either the validity or the invalidity of a sequent.
What is interesting and perhaps surprising is that decidability no longer obtains when we are dealing with some more powerful systems of logic. One of the most important discoveries in modern logic is that mathematics is undecidable. In particular, Gödel's first incompleteness theorem says that any consistent systems of mathematics would have to include statements that can neither be proved or disproved. In other words, it is impossible for there to be a computer program that can tell whether these statements are true.
homepage • top • contact • sitemap
© 2004-2024 Joe Lau & Jonathan Chan
Tim Walz's military record: What to know about potential VP's National Guard service

Democratic presidential candidate Kamala Harris selected Minnesota Governor Tim Walz as her running mate on Tuesday, choosing a progressive yet plain-spoken VP candidate from America’s heartland to help her win over rural, white voters.
“I’m pleased to share that I’ve made my decision: Minnesota Governor Tim Walz will join our campaign as my running mate,” Harris said via text to supporters. “Tim is a battle-tested leader who has an incredible track record of getting things done for Minnesota families. I know that he will bring that same principled leadership to our campaign, and to the office of the vice president.”
We look at Walz, a 60-year-old U.S. Army National Guard veteran, and his military career over the years.
More: Tim Walz is Kamala Harris' VP pick: Minnesota governor named running mate: Live updates
How long was Walz in the military?
Walz served in the military for 24 years, enlisting in the Nebraska National Guard at 17 in 1981 and then transferring to the Minnesota National Guard in 1996. He retired in 2005 to begin his successful run for the U.S. House, representing Minnesota as command sergeant major, among the highest ranks for enlisted soldiers. His battalion went on to deploy to Iraq shortly after Walz's retirement.
Walz specialized in heavy artillery and had proficiency ribbons in sharpshooting and hand grenades.
But during the 21 years that Walz spent working with large artillery pieces, he suffered hearing loss and tinnitus in both ears, Minnesota Public Radio reported. He was allowed to continue his service after undergoing surgery, which partially resolved his hearing loss.
Where did Walz serve, and what did he do in the National Guard?
During his service, Walz responded to natural disasters, including floods and tornadoes in Minnesota and Nebraska, and was deployed overseas for months at a time, according to MPR.
In 2003, he was sent to Italy, where he served with the European Security Force to support the war in Afghanistan. He was also stationed in Norway for joint training with other NATO militaries.
Walz told MPR that he reenlisted in the National Guard after the September 11 attacks but never saw active combat in his years in the military.
Stars and Stripes reported in 2020 that Walz credited his Army experience with helping him steer Minnesota through the COVID-19 pandemic as governor.
As governor of Minnesota, Walz is commander in chief of the 13,000-soldier Minnesota National Guard. “I’m certainly proud of my military service, but it’s one piece of me,” he told Minnesota Public Radio in 2018. “It doesn’t define me.”
Reuters and USA TODAY reporter Tom Vanden Brook contributed to this story.

IMAGES
COMMENTS
Truth Table Calculator. Write down a logical formula and the calculator will instantly compute truth table values for it, with the steps shown. This truth table calculator will provide the truth table values for the given propositional logic formulas. The propositional logic statements can only be true or false.
Most powerful online logic truth table calculator. Easily construct truth tables with steps, generate conclusions, check tautologies, analyze arguments, and more!
For obvious reasons, the truth table test of validity isn't always practical. Fortunately, there's an easier way. The truth assignment test allows us to determine whether an argument is valid much more efficiently. Rather than constructing a truth table and examining all of the possible truth value combinations, we instead consider this ...
Free Truth Table calculator - calculate truth tables for logical expressions.
Simplify logical analysis with our easy-to-use truth table generator. Quickly evaluate your boolean expressions and view the corresponding truth table in real-time. A handy tool for students and professionals.
How does the truth table calculator work? dCode truth table generator interprets the Boolean logical expression and calculates (using Boolean algebra) all the possible combinations of 0 and 1 for each variable (among the Boolean variables requested) in order to make the truth table.
Truth Table Generator This tool generates truth tables for propositional logic formulas. You can enter logical operators in several different formats. For example, the propositional formula p ∧ q → ¬r could be written as p /\ q -> ~r , as p and q => not r, or as p && q -> !r . The connectives ⊤ and ⊥ can be entered as T and F .
Create truth tables with this free truth table generator online. This tool helps you solve and get results of boolean expressions with logic symbols quickly. Visit now to find out more!
A logical truth table calculator is a powerful tool used to simplify the process of evaluating compound propositions. This type of calculator can be incredibly useful when working with complex logic problems, as it eliminates the need for tedious manual calculations required to determine the truth value of each proposition.
Simplogic Simplogic is your logic calculator and toolset. Generate truth tables, simplify logical expressions, and create your own boolean expressions based on your own truth table.
This truth-table calculator for classical logic shows, well, for propositions of classical logic. Featuring a purple munster and a duck, and optionally showing intermediate results, it is one of the better instances of its kind. Use the buttons below (or your keyboard) to enter a proposition, then gently touch the duck to have it calculate the ...
A truth table calculator is a tool used to evaluate logical operations. It takes two or more input combos and produces an output boolean value based on the logic of the operation being performed.
Boolean Algebra expression simplifier & solver. Detailed steps, Logic circuits, KMap, Truth table, & Quizes. All in one boolean expression calculator. Online tool. Learn boolean algebra.
Using a truth table calculator is an efficient way to quickly and accurately calculate logic, Boolean algebra, and other digital circuit problems. This step-by-step guide will help you understand how to use the truth table calculator to easily calculate truth tables with the following steps: Input your variables into the truth table calculator ...
Consistency, Entailment, and Equivalence. On the preceding pages, we saw how to use truth tables and the truth assignment method to determine whether arguments are valid or invalid, and to determine whether an individual proposition is a tautology, contradiction, or contingency. We can use similar methods to study the logical relations between ...
In practice truth assignments are very often presented in the form of tables showing the truth values assigned to a particular formula under all possible assignments of truth values to its propositional variables.
Learn how to use truth tables to test the validity of arguments in logic. Saylor Academy offers a free online course on critical thinking and logic.
A truth assignment for a propositional vocabulary is a function assigning a truth value to each of the proposition constants of the vocabulary. In this book, we use the digit 1 as a synonym for true and 0 as a synonym for false; and we refer to the value of a constant or expression under a truth assignment i by superscripting the constant or ...
2. Circuits and Truth Tables ¶. In this chapter, we review basic notions about gates and learn the relationship between circuits and assignment-based computer programs. This sets the stage for analyzing modern programs. 2.1. Gates and Truth Tables ¶. Here are the four basic gates: P AND Q. P OR Q.
I'm just making the transition from propositional logic to predicate logic and I was wondering how we would use truth tables to test the validity of an argument expressed in predicate logic. Exampl...
This article will explore how logic truth tables can be used to analyze statement forms and evaluate their validity. Truth statements are fundamental building blocks in most philosophical systems, as they form the basis of argumentation and reasoning. Using logic truth tables to assess these statements can reveal insight into truth statements ...
Introduction to Logic - Chapter 4. 4.1 Introduction. Checking logical entailment with truth tables has the merit of being conceptually simple. However, it is not always the most practical method. The number of truth assignments of a language grows exponentially with the number of logical constants. When the number of logical constants in a ...
To help us calculate the truth-values of the WFFs under each assignment, we use the full truth-table method to write down the truth-values of the sentence letters first, and then work out the truth-values of the whole WFFs step by step. The truth-values of the complete WFFs under each assignment is written beneath the main operator of the WFFs.
Democratic presidential candidate Kamala Harris selected Minnesota Governor Tim Walz as her running mate on Tuesday, choosing a progressive yet plain-spoken VP candidate from America's heartland ...