
Statistics Made Easy

How to Test for Normality in R (4 Methods)
Many statistical tests make the assumption that datasets are normally distributed.
There are four common ways to check this assumption in R:
1. (Visual Method) Create a histogram.
- If the histogram is roughly “bell-shaped”, then the data is assumed to be normally distributed.
2. (Visual Method) Create a Q-Q plot.
- If the points in the plot roughly fall along a straight diagonal line, then the data is assumed to be normally distributed.
3. (Formal Statistical Test) Perform a Shapiro-Wilk Test.
- If the p-value of the test is greater than α = .05, then the data is assumed to be normally distributed.
4. (Formal Statistical Test) Perform a Kolmogorov-Smirnov Test.
The following examples show how to use each of these methods in practice.
Method 1: Create a Histogram
The following code shows how to create a histogram for a normally distributed and non-normally distributed dataset in R:

The histogram on the left exhibits a dataset that is normally distributed (roughly a “bell-shape”) and the one on the right exhibits a dataset that is not normally distributed.
Method 2: Create a Q-Q plot
The following code shows how to create a Q-Q plot for a normally distributed and non-normally distributed dataset in R:

The Q-Q plot on the left exhibits a dataset that is normally distributed (the points fall along a straight diagonal line) and the Q-Q plot on the right exhibits a dataset that is not normally distributed.
Method 3: Perform a Shapiro-Wilk Test
The following code shows how to perform a Shapiro-Wilk test on a normally distributed and non-normally distributed dataset in R:
The p-value of the first test is not less than .05, which indicates that the data is normally distributed.
The p-value of the second test is less than .05, which indicates that the data is not normally distributed.
Method 4: Perform a Kolmogorov-Smirnov Test
The following code shows how to perform a Kolmogorov-Smirnov test on a normally distributed and non-normally distributed dataset in R:
How to Handle Non-Normal Data
If a given dataset is not normally distributed, we can often perform one of the following transformations to make it more normally distributed:
1. Log Transformation: Transform the values from x to log(x) .
2. Square Root Transformation: Transform the values from x to √ x .
3. Cube Root Transformation: Transform the values from x to x 1/3 .
By performing these transformations, the dataset typically becomes more normally distributed.
Read this tutorial to see how to perform these transformations in R.
Additional Resources
How to Create Histograms in R How to Create & Interpret a Q-Q Plot in R How to Perform a Shapiro-Wilk Test in R How to Perform a Kolmogorov-Smirnov Test in R
Featured Posts
Hey there. My name is Zach Bobbitt. I have a Masters of Science degree in Applied Statistics and I’ve worked on machine learning algorithms for professional businesses in both healthcare and retail. I’m passionate about statistics, machine learning, and data visualization and I created Statology to be a resource for both students and teachers alike. My goal with this site is to help you learn statistics through using simple terms, plenty of real-world examples, and helpful illustrations.
3 Replies to “How to Test for Normality in R (4 Methods)”
Worked great thank you
it’s a great honor to learn Data Analysis especially using R software. it’s stress-free and it helps push your reasoning . It helps in understanding data collected on field,and encourage to help identify shortcomings of your data.
Leave a Reply Cancel reply
Your email address will not be published. Required fields are marked *
Join the Statology Community
Sign up to receive Statology's exclusive study resource: 100 practice problems with step-by-step solutions. Plus, get our latest insights, tutorials, and data analysis tips straight to your inbox!
By subscribing you accept Statology's Privacy Policy.
Hypothesis Tests in R
This tutorial covers basic hypothesis testing in R.
- Normality tests
- Shapiro-Wilk normality test
- Kolmogorov-Smirnov test
- Comparing central tendencies: Tests with continuous / discrete data
- One-sample t-test : Normally-distributed sample vs. expected mean
- Two-sample t-test : Two normally-distributed samples
- Wilcoxen rank sum : Two non-normally-distributed samples
- Weighted two-sample t-test : Two continuous samples with weights
- Comparing proportions: Tests with categorical data
- Chi-squared goodness of fit test : Sampled frequencies of categorical values vs. expected frequencies
- Chi-squared independence test : Two sampled frequencies of categorical values
- Weighted chi-squared independence test : Two weighted sampled frequencies of categorical values
- Comparing multiple groups: Tests with categorical and continuous / discrete data
- Analysis of Variation (ANOVA) : Normally-distributed samples in groups defined by categorical variable(s)
- Kruskal-Wallace One-Way Analysis of Variance : Nonparametric test of the significance of differences between two or more groups
Hypothesis Testing
Science is "knowledge or a system of knowledge covering general truths or the operation of general laws especially as obtained and tested through scientific method" (Merriam-Webster 2022) .
The idealized world of the scientific method is question-driven , with the collection and analysis of data determined by the formulation of research questions and the testing of hypotheses. Hypotheses are tentative assumptions about what the answers to your research questions may be.
- Formulate questions: How can I understand some phenomenon?
- Literature review: What does existing research say about my questions?
- Formulate hypotheses: What do I think the answers to my questions will be?
- Collect data: What data can I gather to test my hypothesis?
- Test hypotheses: Does the data support my hypothesis?
- Communicate results: Who else needs to know about this?
- Formulate questions: Frame missing knowledge about a phenomenon as research question(s).
- Literature review: A literature review is an investigation of what existing research says about the phenomenon you are studying. A thorough literature review is essential to identify gaps in existing knowledge you can fill, and to avoid unnecessarily duplicating existing research.
- Formulate hypotheses: Develop possible answers to your research questions.
- Collect data: Acquire data that supports or refutes the hypothesis.
- Test hypotheses: Run tools to determine if the data corroborates the hypothesis.
- Communicate results: Share your findings with the broader community that might find them useful.
While the process of knowledge production is, in practice, often more iterative than this waterfall model, the testing of hypotheses is usually a fundamental element of scientific endeavors involving quantitative data.

The Problem of Induction
The scientific method looks to the past or present to build a model that can be used to infer what will happen in the future. General knowledge asserts that given a particular set of conditions, a particular outcome will or is likely to occur.
The problem of induction is that we cannot be 100% certain that what we are assuming is a general principle is not, in fact, specific to the particular set of conditions when we made our empirical observations. We cannot prove that that such principles will hold true under future conditions or different locations that we have not yet experienced (Vickers 2014) .
The problem of induction is often associated with the 18th-century British philosopher David Hume . This problem is especially vexing in the study of human beings, where behaviors are a function of complex social interactions that vary over both space and time.

Falsification
One way of addressing the problem of induction was proposed by the 20th-century Viennese philosopher Karl Popper .
Rather than try to prove a hypothesis is true, which we cannot do because we cannot know all possible situations that will arise in the future, we should instead concentrate on falsification , where we try to find situations where a hypothesis is false. While you cannot prove your hypothesis will always be true, you only need to find one situation where the hypothesis is false to demonstrate that the hypothesis can be false (Popper 1962) .
If a hypothesis is not demonstrated to be false by a particular test, we have corroborated that hypothesis. While corroboration does not "prove" anything with 100% certainty, by subjecting a hypothesis to multiple tests that fail to demonstrate that it is false, we can have increasing confidence that our hypothesis reflects reality.

Null and Alternative Hypotheses
In scientific inquiry, we are often concerned with whether a factor we are considering (such as taking a specific drug) results in a specific effect (such as reduced recovery time).
To evaluate whether a factor results in an effect, we will perform an experiment and / or gather data. For example, in a clinical drug trial, half of the test subjects will be given the drug, and half will be given a placebo (something that appears to be the drug but is actually a neutral substance).

Because the data we gather will usually only be a portion (sample) of total possible people or places that could be affected (population), there is a possibility that the sample is unrepresentative of the population. We use a statistical test that considers that uncertainty when assessing whether an effect is associated with a factor.
- Statistical testing begins with an alternative hypothesis (H 1 ) that states that the factor we are considering results in a particular effect. The alternative hypothesis is based on the research question and the type of statistical test being used.
- Because of the problem of induction , we cannot prove our alternative hypothesis. However, under the concept of falsification , we can evaluate the data to see if there is a significant probability that our data falsifies our alternative hypothesis (Wilkinson 2012) .
- The null hypothesis (H 0 ) states that the factor has no effect. The null hypothesis is the opposite of the alternative hypothesis. The null hypothesis is what we are testing when we perform a hypothesis test.

The output of a statistical test like the t-test is a p -value. A p -value is the probability that any effects we see in the sampled data are the result of random sampling error (chance).
- If a p -value is greater than the significance level (0.05 for 5% significance) we fail to reject the null hypothesis since there is a significant possibility that our results falsify our alternative hypothesis.
- If a p -value is lower than the significance level (0.05 for 5% significance) we reject the null hypothesis and have corroborated (provided evidence for) our alternative hypothesis.
The calculation and interpretation of the p -value goes back to the central limit theorem , which states that random sampling error has a normal distribution.

Using our example of a clinical drug trial, if the mean recovery times for the two groups are close enough together that there is a significant possibility ( p > 0.05) that the recovery times are the same (falsification), we fail to reject the null hypothesis.

However, if the mean recovery times for the two groups are far enough apart that the probability they are the same is under the level of significance ( p < 0.05), we reject the null hypothesis and have corroborated our alternative hypothesis.

Significance means that an effect is "probably caused by something other than mere chance" (Merriam-Webster 2022) .
- The significance level (α) is the threshold for significance and, by convention, is usually 5%, 10%, or 1%, which corresponds to 95% confidence, 90% confidence, or 99% confidence, respectively.
- A factor is considered statistically significant if the probability that the effect we see in the data is a result of random sampling error (the p -value) is below the chosen significance level.
- A statistical test is used to evaluate whether a factor being considered is statistically significant (Gallo 2016) .
Type I vs. Type II Errors
Although we are making a binary choice between rejecting and failing to reject the null hypothesis, because we are using sampled data, there is always the possibility that the choice we have made is an error.
There are two types of errors that can occur in hypothesis testing.
- Type I error (false positive) occurs when a low p -value causes us to reject the null hypothesis, but the factor does not actually result in the effect.
- Type II error (false negative) occurs when a high p -value causes us to fail to reject the null hypothesis, but the factor does actually result in the effect.
The numbering of the errors reflects the predisposition of the scientific method to be fundamentally skeptical . Accepting a fact about the world as true when it is not true is considered worse than rejecting a fact about the world that actually is true.

Statistical Significance vs. Importance
When we fail to reject the null hypothesis, we have found information that is commonly called statistically significant . But there are multiple challenges with this terminology.
First, statistical significance is distinct from importance (NIST 2012) . For example, if sampled data reveals a statistically significant difference in cancer rates, that does not mean that the increased risk is important enough to justify expensive mitigation measures. All statistical results require critical interpretation within the context of the phenomenon being observed. People with different values and incentives can have different interpretations of whether statistically significant results are important.
Second, the use of 95% probability for defining confidence intervals is an arbitrary convention. This creates a good vs. bad binary that suggests a "finality and certitude that are rarely justified." Alternative approaches like Beyesian statistics that express results as probabilities can offer more nuanced ways of dealing with complexity and uncertainty (Clayton 2022) .
Science vs. Non-science
Not all ideas can be falsified, and Popper uses the distinction between falsifiable and non-falsifiable ideas to make a distinction between science and non-science. In order for an idea to be science it must be an idea that can be demonstrated to be false.
While Popper asserts there is still value in ideas that are not falsifiable, such ideas are not science in his conception of what science is. Such non-science ideas often involve questions of subjective values or unseen forces that are complex, amorphous, or difficult to objectively observe.
| Falsifiable (Science) | Non-Falsifiable (Non-Science) |
|---|---|
| Murder death rates by firearms tend to be higher in countries with higher gun ownership rates | Murder is wrong |
| Marijuana users may be more likely than nonusers to | The benefits of marijuana outweigh the risks |
| Job candidates who meaningfully research the companies they are interviewing with have higher success rates | Prayer improves success in job interviews |
Example Data
As example data, this tutorial will use a table of anonymized individual responses from the CDC's Behavioral Risk Factor Surveillance System . The BRFSS is a "system of health-related telephone surveys that collect state data about U.S. residents regarding their health-related risk behaviors, chronic health conditions, and use of preventive services" (CDC 2019) .
A CSV file with the selected variables used in this tutorial is available here and can be imported into R with read.csv() .
Guidance on how to download and process this data directly from the CDC website is available here...
Variable Types
The publicly-available BRFSS data contains a wide variety of discrete, ordinal, and categorical variables. Variables often contain special codes for non-responsiveness or missing (NA) values. Examples of how to clean these variables are given here...
The BRFSS has a codebook that gives the survey questions associated with each variable, and the way that responses are encoded in the variable values.

Normality Tests
Tests are commonly divided into two groups depending on whether they are built on the assumption that the continuous variable has a normal distribution.
- Parametric tests presume a normal distribution.
- Non-parametric tests can work with normal and non-normal distributions.
The distinction between parametric and non-parametric techniques is especially important when working with small numbers of samples (less than 40 or so) from a larger population.
The normality tests given below do not work with large numbers of values, but with many statistical techniques, violations of normality assumptions do not cause major problems when large sample sizes are used. (Ghasemi and Sahediasi 2012) .
The Shapiro-Wilk Normality Test
- Data: A continuous or discrete sampled variable
- R Function: shapiro.test()
- Null hypothesis (H 0 ): The population distribution from which the sample is drawn is not normal
- History: Samuel Sanford Shapiro and Martin Wilk (1965)
This is an example with random values from a normal distribution.
This is an example with random values from a uniform (non-normal) distribution.
The Kolmogorov-Smirnov Test
The Kolmogorov-Smirnov is a more-generalized test than the Shapiro-Wilks test that can be used to test whether a sample is drawn from any type of distribution.
- Data: A continuous or discrete sampled variable and a reference probability distribution
- R Function: ks.test()
- Null hypothesis (H 0 ): The population distribution from which the sample is drawn does not match the reference distribution
- History: Andrey Kolmogorov (1933) and Nikolai Smirnov (1948)
- pearson.test() The Pearson Chi-square Normality Test from the nortest library. Lower p-values (closer to 0) means to reject the reject the null hypothesis that the distribution IS normal.
Modality Tests of Samples
Comparing two central tendencies: tests with continuous / discrete data, one sample t-test (two-sided).
The one-sample t-test tests the significance of the difference between the mean of a sample and an expected mean.
- Data: A continuous or discrete sampled variable and a single expected mean (μ)
- Parametric (normal distributions)
- R Function: t.test()
- Null hypothesis (H 0 ): The means of the sampled distribution matches the expected mean.
- History: William Sealy Gosset (1908)
t = ( Χ - μ) / (σ̂ / √ n )
- t : The value of t used to find the p-value
- Χ : The sample mean
- μ: The population mean
- σ̂: The estimate of the standard deviation of the population (usually the stdev of the sample
- n : The sample size
T-tests should only be used when the population is at least 20 times larger than its respective sample. If the sample size is too large, the low p-value makes the insignificant look significant. .
For example, we test a hypothesis that the mean weight in IL in 2020 is different than the 2005 continental mean weight.
Walpole et al. (2012) estimated that the average adult weight in North America in 2005 was 178 pounds. We could presume that Illinois is a comparatively normal North American state that would follow the trend of both increased age and increased weight (CDC 2021) .

The low p-value leads us to reject the null hypothesis and corroborate our alternative hypothesis that mean weight changed between 2005 and 2020 in Illinois.
One Sample T-Test (One-Sided)
Because we were expecting an increase, we can modify our hypothesis that the mean weight in 2020 is higher than the continental weight in 2005. We can perform a one-sided t-test using the alternative="greater" parameter.
The low p-value leads us to again reject the null hypothesis and corroborate our alternative hypothesis that mean weight in 2020 is higher than the continental weight in 2005.
Note that this does not clearly evaluate whether weight increased specifically in Illinois, or, if it did, whether that was caused by an aging population or decreasingly healthy diets. Hypotheses based on such questions would require more detailed analysis of individual data.
Although we can see that the mean cancer incidence rate is higher for counties near nuclear plants, there is the possiblity that the difference in means happened by accident and the nuclear plants have nothing to do with those higher rates.
The t-test allows us to test a hypothesis. Note that a t-test does not "prove" or "disprove" anything. It only gives the probability that the differences we see between two areas happened by chance. It also does not evaluate whether there are other problems with the data, such as a third variable, or inaccurate cancer incidence rate estimates.

Note that this does not prove that nuclear power plants present a higher cancer risk to their neighbors. It simply says that the slightly higher risk is probably not due to chance alone. But there are a wide variety of other other related or unrelated social, environmental, or economic factors that could contribute to this difference.
Box-and-Whisker Chart
One visualization commonly used when comparing distributions (collections of numbers) is a box-and-whisker chart. The boxes show the range of values in the middle 25% to 50% to 75% of the distribution and the whiskers show the extreme high and low values.

Although Google Sheets does not provide the capability to create box-and-whisker charts, Google Sheets does have candlestick charts , which are similar to box-and-whisker charts, and which are normally used to display the range of stock price changes over a period of time.
This video shows how to create a candlestick chart comparing the distributions of cancer incidence rates. The QUARTILE() function gets the values that divide the distribution into four equally-sized parts. This shows that while the range of incidence rates in the non-nuclear counties are wider, the bulk of the rates are below the rates in nuclear counties, giving a visual demonstration of the numeric output of our t-test.
While categorical data can often be reduced to dichotomous data and used with proportions tests or t-tests, there are situations where you are sampling data that falls into more than two categories and you would like to make hypothesis tests about those categories. This tutorial describes a group of tests that can be used with that type of data.
Two-Sample T-Test
When comparing means of values from two different groups in your sample, a two-sample t-test is in order.
The two-sample t-test tests the significance of the difference between the means of two different samples.
- Two normally-distributed, continuous or discrete sampled variables, OR
- A normally-distributed continuous or sampled variable and a parallel dichotomous variable indicating what group each of the values in the first variable belong to
- Null hypothesis (H 0 ): The means of the two sampled distributions are equal.
For example, given the low incomes and delicious foods prevalent in Mississippi, we might presume that average weight in Mississippi would be higher than in Illinois.

We test a hypothesis that the mean weight in IL in 2020 is less than the 2020 mean weight in Mississippi.
The low p-value leads us to reject the null hypothesis and corroborate our alternative hypothesis that mean weight in Illinois is less than in Mississippi.
While the difference in means is statistically significant, it is small (182 vs. 187), which should lead to caution in interpretation that you avoid using your analysis simply to reinforce unhelpful stigmatization.
Wilcoxen Rank Sum Test (Mann-Whitney U-Test)
The Wilcoxen rank sum test tests the significance of the difference between the means of two different samples. This is a non-parametric alternative to the t-test.
- Data: Two continuous sampled variables
- Non-parametric (normal or non-normal distributions)
- R Function: wilcox.test()
- Null hypothesis (H 0 ): For randomly selected values X and Y from two populations, the probability of X being greater than Y is equal to the probability of Y being greater than X.
- History: Frank Wilcoxon (1945) and Henry Mann and Donald Whitney (1947)
The test is is implemented with the wilcox.test() function.
- When the test is performed on one sample in comparison to an expected value around which the distribution is symmetrical (μ), the test is known as a Mann-Whitney U test .
- When the test is performed to compare two samples, the test is known as a Wilcoxon rank sum test .
For this example, we will use AVEDRNK3: During the past 30 days, on the days when you drank, about how many drinks did you drink on the average?
- 1 - 76: Number of drinks
- 77: Don’t know/Not sure
- 99: Refused
- NA: Not asked or Missing
The histogram clearly shows this to be a non-normal distribution.

Continuing the comparison of Illinois and Mississippi from above, we might presume that with all that warm weather and excellent food in Mississippi, they might be inclined to drink more. The means of average number of drinks per month seem to suggest that Mississippians do drink more than Illinoians.
We can test use wilcox.test() to test a hypothesis that the average amount of drinking in Illinois is different than in Mississippi. Like the t-test, the alternative can be specified as two-sided or one-sided, and for this example we will test whether the sampled Illinois value is indeed less than the Mississippi value.
The low p-value leads us to reject the null hypothesis and corroborates our hypothesis that average drinking is lower in Illinois than in Mississippi. As before, this tells us nothing about why this is the case.
Weighted Two-Sample T-Test
The downloadable BRFSS data is raw, anonymized survey data that is biased by uneven geographic coverage of survey administration (noncoverage) and lack of responsiveness from some segments of the population (nonresponse). The X_LLCPWT field (landline, cellphone weighting) is a weighting factor added by the CDC that can be assigned to each response to compensate for these biases.
The wtd.t.test() function from the weights library has a weights parameter that can be used to include a weighting factor as part of the t-test.
Comparing Proportions: Tests with Categorical Data
Chi-squared goodness of fit.
- Tests the significance of the difference between sampled frequencies of different values and expected frequencies of those values
- Data: A categorical sampled variable and a table of expected frequencies for each of the categories
- R Function: chisq.test()
- Null hypothesis (H 0 ): The relative proportions of categories in one variable are different from the expected proportions
- History: Karl Pearson (1900)
- Example Question: Are the voting preferences of voters in my district significantly different from the current national polls?
For example, we test a hypothesis that smoking rates changed between 2000 and 2020.
In 2000, the estimated rate of adult smoking in Illinois was 22.3% (Illinois Department of Public Health 2004) .
The variable we will use is SMOKDAY2: Do you now smoke cigarettes every day, some days, or not at all?
- 1: Current smoker - now smokes every day
- 2: Current smoker - now smokes some days
- 3: Not at all
- 7: Don't know
- NA: Not asked or missing - NA is used for people who have never smoked
We subset only yes/no responses in Illinois and convert into a dummy variable (yes = 1, no = 0).
The listing of the table as percentages indicates that smoking rates were halved between 2000 and 2020, but since this is sampled data, we need to run a chi-squared test to make sure the difference can't be explained by the randomness of sampling.
In this case, the very low p-value leads us to reject the null hypothesis and corroborates the alternative hypothesis that smoking rates changed between 2000 and 2020.
Chi-Squared Contingency Analysis / Test of Independence
- Tests the significance of the difference between frequencies between two different groups
- Data: Two categorical sampled variables
- Null hypothesis (H 0 ): The relative proportions of one variable are independent of the second variable.
We can also compare categorical proportions between two sets of sampled categorical variables.
The chi-squared test can is used to determine if two categorical variables are independent. What is passed as the parameter is a contingency table created with the table() function that cross-classifies the number of rows that are in the categories specified by the two categorical variables.
The null hypothesis with this test is that the two categories are independent. The alternative hypothesis is that there is some dependency between the two categories.
For this example, we can compare the three categories of smokers (daily = 1, occasionally = 2, never = 3) across the two categories of states (Illinois and Mississippi).

The low p-value leads us to reject the null hypotheses that the categories are independent and corroborates our hypotheses that smoking behaviors in the two states are indeed different.
p-value = 1.516e-09
Weighted Chi-Squared Contingency Analysis
As with the weighted t-test above, the weights library contains the wtd.chi.sq() function for incorporating weighting into chi-squared contingency analysis.
As above, the even lower p-value leads us to again reject the null hypothesis that smoking behaviors are independent in the two states.
Suppose that the Macrander campaign would like to know how partisan this election is. If people are largely choosing to vote along party lines, the campaign will seek to get their base voters out to the polls. If people are splitting their ticket, the campaign may focus their efforts more broadly.
In the example below, the Macrander campaign took a small poll of 30 people asking who they wished to vote for AND what party they most strongly affiliate with.
The output of table() shows fairly strong relationship between party affiliation and candidates. Democrats tend to vote for Macrander, while Republicans tend to vote for Stewart, while independents all vote for Miller.
This is reflected in the very low p-value from the chi-squared test. This indicates that there is a very low probability that the two categories are independent. Therefore we reject the null hypothesis.
In contrast, suppose that the poll results had showed there were a number of people crossing party lines to vote for candidates outside their party. The simulated data below uses the runif() function to randomly choose 50 party names.
The contingency table() shows no clear relationship between party affiliation and candidate. This is validated quantitatively by the chi-squared test. The fairly high p-value of 0.4018 indicates a 40% chance that the two categories are independent. Therefore, we fail to reject the null hypothesis and the campaign should focus their efforts on the broader electorate.
The warning message given by the chisq.test() function indicates that the sample size is too small to make an accurate analysis. The simulate.p.value = T parameter adds Monte Carlo simulation to the test to improve the estimation and get rid of the warning message. However, the best way to get rid of this message is to get a larger sample.
Comparing Categorical and Continuous Variables
Analysis of variation (anova).
Analysis of Variance (ANOVA) is a test that you can use when you have a categorical variable and a continuous variable. It is a test that considers variability between means for different categories as well as the variability of observations within groups.
There are a wide variety of different extensions of ANOVA that deal with covariance (ANCOVA), multiple variables (MANOVA), and both of those together (MANCOVA). These techniques can become quite complicated and also assume that the values in the continuous variables have a normal distribution.
- Data: One or more categorical (independent) variables and one continuous (dependent) sampled variable
- R Function: aov()
- Null hypothesis (H 0 ): There is no difference in means of the groups defined by each level of the categorical (independent) variable
- History: Ronald Fisher (1921)
- Example Question: Do low-, middle- and high-income people vary in the amount of time they spend watching TV?
As an example, we look at the continuous weight variable (WEIGHT2) split into groups by the eight income categories in INCOME2: Is your annual household income from all sources?
- 1: Less than $10,000
- 2: $10,000 to less than $15,000
- 3: $15,000 to less than $20,000
- 4: $20,000 to less than $25,000
- 5: $25,000 to less than $35,000
- 6: $35,000 to less than $50,000
- 7: $50,000 to less than $75,000)
- 8: $75,000 or more
The barplot() of means does show variation among groups, although there is no clear linear relationship between income and weight.

To test whether this variation could be explained by randomness in the sample, we run the ANOVA test.
The low p-value leads us to reject the null hypothesis that there is no difference in the means of the different groups, and corroborates the alternative hypothesis that mean weights differ based on income group.
However, it gives us no clear model for describing that relationship and offers no insights into why income would affect weight, especially in such a nonlinear manner.
Suppose you are performing research into obesity in your city. You take a sample of 30 people in three different neighborhoods (90 people total), collecting information on health and lifestyle. Two variables you collect are height and weight so you can calculate body mass index . Although this index can be misleading for some populations (notably very athletic people), ordinary sedentary people can be classified according to BMI:
Average BMI in the US from 2007-2010 was around 28.6 and rising, standard deviation of around 5 .
You would like to know if there is a difference in BMI between different neighborhoods so you can know whether to target specific neighborhoods or make broader city-wide efforts. Since you have more than two groups, you cannot use a t-test().
Kruskal-Wallace One-Way Analysis of Variance
A somewhat simpler test is the Kruskal-Wallace test which is a nonparametric analogue to ANOVA for testing the significance of differences between two or more groups.
- R Function: kruskal.test()
- Null hypothesis (H 0 ): The samples come from the same distribution.
- History: William Kruskal and W. Allen Wallis (1952)
For this example, we will investigate whether mean weight varies between the three major US urban states: New York, Illinois, and California.

To test whether this variation could be explained by randomness in the sample, we run the Kruskal-Wallace test.
The low p-value leads us to reject the null hypothesis that the samples come from the same distribution. This corroborates the alternative hypothesis that mean weights differ based on state.
A convienent way of visualizing a comparison between continuous and categorical data is with a box plot , which shows the distribution of a continuous variable across different groups:

A percentile is the level at which a given percentage of the values in the distribution are below: the 5th percentile means that five percent of the numbers are below that value.
The quartiles divide the distribution into four parts. 25% of the numbers are below the first quartile. 75% are below the third quartile. 50% are below the second quartile, making it the median.
Box plots can be used with both sampled data and population data.
The first parameter to the box plot is a formula: the continuous variable as a function of (the tilde) the second variable. A data= parameter can be added if you are using variables in a data frame.
The chi-squared test can be used to determine if two categorical variables are independent of each other.

Statistical Tests and Assumptions
Normality Test in R
Many of the statistical methods including correlation, regression, t tests, and analysis of variance assume that the data follows a normal distribution or a Gaussian distribution. These tests are called parametric tests, because their validity depends on the distribution of the data.
Normality and the other assumptions made by these tests should be taken seriously to draw reliable interpretation and conclusions of the research.
With large enough sample sizes (> 30 or 40), there’s a pretty good chance that the data will be normally distributed; or at least close enough to normal that you can get away with using parametric tests, such as t-test (central limit theorem).
In this chapter, you will learn how to check the normality of the data in R by visual inspection ( QQ plots and density distributions ) and by significance tests ( Shapiro-Wilk test ).
Prerequisites
Examples of distribution shapes, visual methods, shapiro-wilk’s normality test, related book.
Make sure you have installed the following R packages:
- tidyverse for data manipulation and visualization
- ggpubr for creating easily publication ready plots
- rstatix provides pipe-friendly R functions for easy statistical analyses
Start by loading the packages:
We’ll use the ToothGrowth dataset. Inspect the data by displaying some random rows by groups:
- Normal distribution
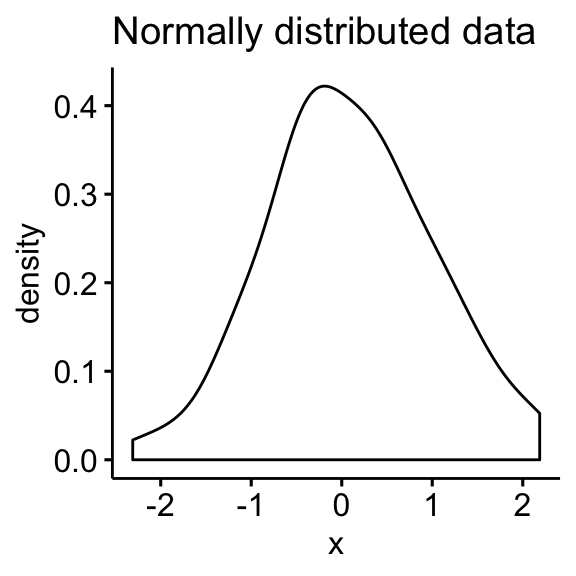
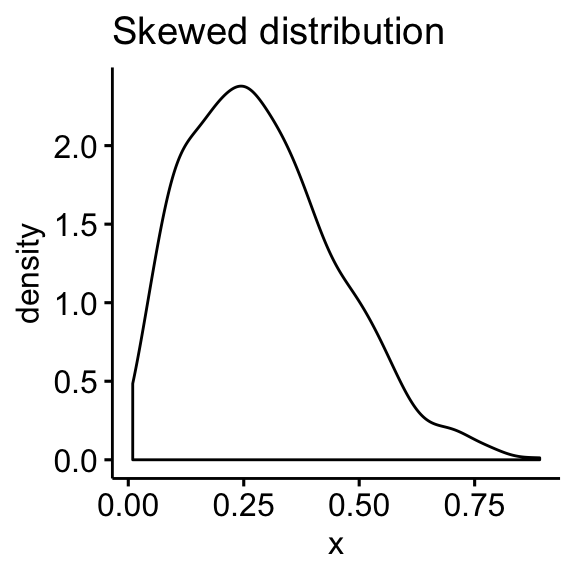
- Skewed distributions
Check normality in R
Question: We want to test if the variable len (tooth length) is normally distributed.
Density plot and Q-Q plot can be used to check normality visually.
- Density plot : the density plot provides a visual judgment about whether the distribution is bell shaped.
- QQ plot : QQ plot (or quantile-quantile plot) draws the correlation between a given sample and the normal distribution. A 45-degree reference line is also plotted. In a QQ plot, each observation is plotted as a single dot. If the data are normal, the dots should form a straight line.
As all the points fall approximately along this reference line, we can assume normality.
Visual inspection, described in the previous section, is usually unreliable. It’s possible to use a significance test comparing the sample distribution to a normal one in order to ascertain whether data show or not a serious deviation from normality.
There are several methods for evaluate normality, including the Kolmogorov-Smirnov (K-S) normality test and the Shapiro-Wilk’s test .
The null hypothesis of these tests is that “sample distribution is normal”. If the test is significant , the distribution is non-normal.
Shapiro-Wilk’s method is widely recommended for normality test and it provides better power than K-S. It is based on the correlation between the data and the corresponding normal scores (Ghasemi and Zahediasl 2012) .
Note that, normality test is sensitive to sample size. Small samples most often pass normality tests. Therefore, it’s important to combine visual inspection and significance test in order to take the right decision.
The R function shapiro_test() [rstatix package] provides a pipe-friendly framework to compute Shapiro-Wilk test for one or multiple variables. It also supports a grouped data. It’s a wrapper around R base function shapiro.test() .
- Shapiro test for one variable:
From the output above, the p-value > 0.05 implying that the distribution of the data are not significantly different from normal distribution. In other words, we can assume the normality.
- Shapiro test for grouped data:
- Shapiro test for multiple variables:
This chapter describes how to check the normality of a data using QQ-plot and Shapiro-Wilk test.
Note that, if your sample size is greater than 50, the normal QQ plot is preferred because at larger sample sizes the Shapiro-Wilk test becomes very sensitive even to a minor deviation from normality.
Consequently, we should not rely on only one approach for assessing the normality. A better strategy is to combine visual inspection and statistical test.
Ghasemi, Asghar, and Saleh Zahediasl. 2012. “Normality Tests for Statistical Analysis: A Guide for Non-Statisticians.” Int J Endocrinol Metab 10 (2): 486–89. doi: 10.5812/ijem.3505 .
Recommended for you
This section contains best data science and self-development resources to help you on your path.
Coursera - Online Courses and Specialization
Data science.
- Course: Machine Learning: Master the Fundamentals by Stanford
- Specialization: Data Science by Johns Hopkins University
- Specialization: Python for Everybody by University of Michigan
- Courses: Build Skills for a Top Job in any Industry by Coursera
- Specialization: Master Machine Learning Fundamentals by University of Washington
- Specialization: Statistics with R by Duke University
- Specialization: Software Development in R by Johns Hopkins University
- Specialization: Genomic Data Science by Johns Hopkins University
Popular Courses Launched in 2020
- Google IT Automation with Python by Google
- AI for Medicine by deeplearning.ai
- Epidemiology in Public Health Practice by Johns Hopkins University
- AWS Fundamentals by Amazon Web Services
Trending Courses
- The Science of Well-Being by Yale University
- Google IT Support Professional by Google
- Python for Everybody by University of Michigan
- IBM Data Science Professional Certificate by IBM
- Business Foundations by University of Pennsylvania
- Introduction to Psychology by Yale University
- Excel Skills for Business by Macquarie University
- Psychological First Aid by Johns Hopkins University
- Graphic Design by Cal Arts
Amazing Selling Machine
- Free Training - How to Build a 7-Figure Amazon FBA Business You Can Run 100% From Home and Build Your Dream Life! by ASM
Books - Data Science
- Practical Guide to Cluster Analysis in R by A. Kassambara (Datanovia)
- Practical Guide To Principal Component Methods in R by A. Kassambara (Datanovia)
- Machine Learning Essentials: Practical Guide in R by A. Kassambara (Datanovia)
- R Graphics Essentials for Great Data Visualization by A. Kassambara (Datanovia)
- GGPlot2 Essentials for Great Data Visualization in R by A. Kassambara (Datanovia)
- Network Analysis and Visualization in R by A. Kassambara (Datanovia)
- Practical Statistics in R for Comparing Groups: Numerical Variables by A. Kassambara (Datanovia)
- Inter-Rater Reliability Essentials: Practical Guide in R by A. Kassambara (Datanovia)
- R for Data Science: Import, Tidy, Transform, Visualize, and Model Data by Hadley Wickham & Garrett Grolemund
- Hands-On Machine Learning with Scikit-Learn, Keras, and TensorFlow: Concepts, Tools, and Techniques to Build Intelligent Systems by Aurelien Géron
- Practical Statistics for Data Scientists: 50 Essential Concepts by Peter Bruce & Andrew Bruce
- Hands-On Programming with R: Write Your Own Functions And Simulations by Garrett Grolemund & Hadley Wickham
- An Introduction to Statistical Learning: with Applications in R by Gareth James et al.
- Deep Learning with R by François Chollet & J.J. Allaire
- Deep Learning with Python by François Chollet
Version: Français
Comment ( 1 )
can you please give a reference to the book or paper that support the claims you do in this lesson: eg. “Note that, normality test is sensitive to sample size. Small samples most often pass normality tests. Therefore, it’s important to combine visual inspection and significance test in order to take the right decision.”
Give a comment Cancel reply
Course curriculum.
- Normality Test in R 10 mins
- Homogeneity of Variance Test in R 10 mins
- Mauchly's Test of Sphericity in R 15 mins
- Transform Data to Normal Distribution in R 15 mins

Alboukadel Kassambara
Role : founder of datanovia.
- Website : https://www.datanovia.com/en
- Experience : >10 years
- Specialist in : Bioinformatics and Cancer Biology
Introduction to Statistics with R
6.2 hypothesis tests, 6.2.1 illustrating a hypothesis test.
Let’s say we have a batch of chocolate bars, and we’re not sure if they are from Theo’s. What can the weight of these bars tell us about the probability that these are Theo’s chocolate?
Now, let’s perform a hypothesis test on this chocolate of an unknown origin.
What is the sampling distribution of the bar weight under the null hypothesis that the bars from Theo’s weigh 40 grams on average? We’ll need to specify the standard deviation to obtain the sampling distribution, and here we’ll use \(\sigma_X = 2\) (since that’s the value we used for the distribution we sampled from).
The null hypothesis is \[H_0: \mu = 40\] since we know the mean weight of Theo’s chocolate bars is 40 grams.
The sample distribution of the sample mean is: \[ \overline{X} \sim {\cal N}\left(\mu, \frac{\sigma}{\sqrt{n}}\right) = {\cal N}\left(40, \frac{2}{\sqrt{20}}\right). \] We can visualize the situation by plotting the p.d.f. of the sampling distribution under \(H_0\) along with the location of our observed sample mean.

6.2.2 Hypothesis Tests for Means
6.2.2.1 known standard deviation.
It is simple to calculate a hypothesis test in R (in fact, we already implicitly did this in the previous section). When we know the population standard deviation, we use a hypothesis test based on the standard normal, known as a \(z\) -test. Here, let’s assume \(\sigma_X = 2\) (because that is the standard deviation of the distribution we simulated from above) and specify the alternative hypothesis to be \[ H_A: \mu \neq 40. \] We will the z.test() function from the BSDA package, specifying the confidence level via conf.level , which is \(1 - \alpha = 1 - 0.05 = 0.95\) , for our test:
6.2.2.2 Unknown Standard Deviation
If we do not know the population standard deviation, we typically use the t.test() function included in base R. We know that: \[\frac{\overline{X} - \mu}{\frac{s_x}{\sqrt{n}}} \sim t_{n-1},\] where \(t_{n-1}\) denotes Student’s \(t\) distribution with \(n - 1\) degrees of freedom. We only need to supply the confidence level here:
We note that the \(p\) -value here (rounded to 4 decimal places) is 0.0031, so again, we can detect it’s not likely that these bars are from Theo’s. Even with a very small sample, the difference is large enough (and the standard deviation small enough) that the \(t\) -test can detect it.
6.2.3 Two-sample Tests
6.2.3.1 unpooled two-sample t-test.
Now suppose we have two batches of chocolate bars, one of size 40 and one of size 45. We want to test whether they come from the same factory. However we have no information about the distributions of the chocolate bars. Therefore, we cannot conduct a one sample t-test like above as that would require some knowledge about \(\mu_0\) , the population mean of chocolate bars.
We will generate the samples from normal distribution with mean 45 and 47 respectively. However, let’s assume we do not know this information. The population standard deviation of the distributions we are sampling from are both 2, but we will assume we do not know that either. Let us denote the unknown true population means by \(\mu_1\) and \(\mu_2\) .

Consider the test \(H_0:\mu_1=\mu_2\) versus \(H_1:\mu_1\neq\mu_2\) . We can use R function t.test again, since this function can perform one- and two-sided tests. In fact, t.test assumes a two-sided test by default, so we do not have to specify that here.
The p-value is much less than .05, so we can quite confidently reject the null hypothesis. Indeed, we know from simulating the data that \(\mu_1\neq\mu_2\) , so our test led us to the correct conclusion!
Consider instead testing \(H_0:\mu_1=\mu_2\) versus \(H_1:\mu_1\leq\mu_2\) .
As we would expect, this test also rejects the null hypothesis. One-sided tests are more common in practice as they provide a more principled description of the relationship between the datasets. For example, if you are comparing your new drug’s performance to a “gold standard”, you really only care if your drug’s performance is “better” (a one-sided alternative), and not that your drug’s performance is merely “different” (a two-sided alternative).
6.2.3.2 Pooled Two-sample t-test
Suppose you knew that the samples are coming from distributions with same standard deviations. Then it makes sense to carry out a pooled 2 sample t-test. You specify this in the t.test function as follows.
6.2.3.3 Paired t-test
Suppose we take a batch of chocolate bars and stamp the Theo’s logo on them. We want to know if the stamping process significantly changes the weight of the chocolate bars. Let’s suppose that the true change in weight is distributed as a \({\cal N}(-0.3, 0.2^2)\) random variable:

Let \(\mu_1\) and \(\mu_2\) be the true means of the distributions of chocolate weights before and after the stamping process. Suppose we want to test \(H_0:\mu_1=\mu_2\) versus \(\mu_1\neq\mu_2\) . We can use the R function t.test() for this by choosing paired = TRUE , which indicates that we are looking at pairs of observations corresponding to the same experimental subject and testing whether or not the difference in distribution means is zero.
We can also perform the same test as a one sample t-test using choc.after - choc.batch .
Notice that we get the exact same \(p\) -value for these two tests.
Since the p-value is less than .05, we reject the null hypothesis at level .05. Hence, we have enough evidence in the data to claim that stamping a chocolate bar significantly reduces its weight.
6.2.4 Tests for Proportions
Let’s look at the proportion of Theo’s chocolate bars with a weight exceeding 38g:
Going back to that first batch of 20 chocolate bars of unknown origin, let’s see if we can test whether they’re from Theo’s based on the proportion weighing > 38g.
Recall from our test on the means that we rejected the null hypothesis that the means from the two batches were equal. In this case, a one-sided test is appropiate, and our hypothesis is:
Null hypothesis: \(H_0: p = 0.85\) . Alternative: \(H_A: p > 0.85\) .
We want to test this hypothesis at a level \(\alpha = 0.05\) .
In R, there is a function called prop.test() that you can use to perform tests for proportions. Note that prop.test() only gives you an approximate result.
Similarly, you can use the binom.test() function for an exact result.
The \(p\) -value for both tests is around 0.18, which is much greater than 0.05. So, we cannot reject the hypothesis that the unknown bars come from Theo’s. This is not because the tests are less accurate than the ones we ran before, but because we are testing a less sensitive measure: the proportion weighing > 38 grams, rather than the mean weights. Also, note that this doesn’t mean that we can conclude that these bars do come from Theo’s – why not?
The prop.test() function is the more versatile function in that it can deal with contingency tables, larger number of groups, etc. The binom.test() function gives you exact results, but you can only apply it to one-sample questions.
6.2.5 Power
Let’s think about when we reject the null hypothesis. We would reject the null hypothesis if we observe data with too small of a \(p\) -value. We can calculate the critical value where we would reject the null if we were to observe data that would lead to a more extreme value.
Suppose we take a sample of chocolate bars of size n = 20 , and our null hypothesis is that the bars come from Theo’s ( \(H_0\) : mean = 40, sd = 2 ). Then for a one-sided test (versus larger alternatives), we can calculate the critical value by using the quantile function in R, specifiying the mean and sd of the sampling distribution of \(\overline X\) under \(H_0\) :
Now suppose we want to calculate the power of our hypothesis test: the probability of rejecting the null hypothesis when the null hypothesis is false. In order to do so, we need to compare the null to a specific alternative, so we choose \(H_A\) : mean = 42, sd = 2 . Then the probability that we reject the null under this specific alternative is
We can use R to perform the same calculations using the power.z.test from the asbio package:
Intro to hypothesis testing
Hypothesis testing is all about answering the question: for a parameter \(\theta\) , is a parameter value of \(\theta_0\) consistent with the data in our observed sample?
We call this is the null hypothesis and write
\[ H_0 : \theta = \theta_0 \]
where this means that true (population) value of a parameter \(\theta\) is equal to some value \(\theta_0\) .
What do we do next? We assume that \(\theta = \theta_0\) in the population, and then check if this assumption is compatible with our observed data. The population with \(\theta = \theta_0\) corresponds to a probability distribution, which we call the null distribution .
Let’s make this concrete. Suppose that we observe data \(2, 3, 7\) and we know that our data comes from a normal distribution with known variance \(\sigma^2 = 2\) . Realistically, we won’t know \(\sigma^2\) , or that our data is normal, but we’ll work with these assumptions for now and relax them later.
Let’s suppose we’re interested in the population mean. Let’s guess that the population mean is 8. In this case we would write the null hypothesis as \(H_0 : \mu = 8\) . This is a ridiculous guess for the population mean given our data, but it’ll illustrate our point. Our null distribution is then \(\mathrm{Normal}(8, 2)\) .
Now that we have a null distribution, we need to dream up a test statistic . In this class, you’ll always be given a test statistic. For now we’ll use the T statistic.
\[ Z = {\bar x - \mu_0 \over \mathrm{se}\left(\bar x \right)} = {\bar x - \mu_0 \over {\sigma \over \sqrt n}} = {4 \over \sqrt \frac 23} \approx 4.9 \]
Recall: a statistic \(T(X)\) is a function from a random sample into the real line. Since statistics are functions of random samples, they are themselves random variables.
Test statistics are chosen to have two important properties:
- They need to relate to the population parameter we’re interested in measuring
- We need to know their sampling distributions
Sampling distributions you say! Why do test statistics have sampling distributions? Because we’re just taking a function of a random sample.
For this example, we know that
\[ Z \sim \mathrm{Normal}(0, 1) \]
and now we ask how probable is this statistic given that we have assumed that null distribution is true .
The idea is that if this number is very small, then our null distribution can’t be correct: we shouldn’t observe highly unlikely statistics. This means that hypothesis testing is a form of falsification testing .
For the example above, we are interested in the probability of observing a more extreme test statistic given the null distribution, which in this case is:
\[ P(|Z| > 4.9) = P(Z < -4.9) + P(Z > 4.9) \approx 9.6 \cdot 10^{-7} \]
This probability is called a p-value . Since it’s very small, we conclude that the null hypothesis is not realistic. In other words, the population mean is statistically distinguishable from 8 (whether or not it is practically distinguishable from 8 is entirely another matter).
This is the just of hypothesis testing. Of course there’s a bunch of other associated nonsense that obscures the basic idea, which we’ll dive into next.
Things that can go wrong
False positives.
We need to be concerned about rejecting the null hypothesis when the null hypothesis is true. This is called a false positive or a Type I error.
If the null hypothesis is true, and we calculate a statistic like we did above, we still expect to see a value of p-value of \(9.6 \cdot 10^{-7}\) about \(9.6 \cdot 10^{-5}\) percent of the time. For small p-values this isn’t an issue, but let’s consider a different null hypothesis of \(\mu_0 = 3.9\) . Now
\[ Z = {\bar x - \mu_0 \over {\sigma \over \sqrt n}} = {4 - 3.9 \over \sqrt \frac 23} \approx 0.12 \]
and our corresponding p-value is
\[ P(|Z| > 0.12) = P(Z < -0.12) + P(Z > 0.12) \approx 0.9 \]
and we see that this is quite probable! We should definitely not reject the null hypothesis!
This leads us to a new question: when should we reject the null hypothesis? A standard choice is to set an acceptable probability for a false positive \(\alpha\) . One arbitrary but common choice is to set \(\alpha = 0.05\) , which means we are okay with a \({1 \over 20}\) chance of a false positive. We should then reject the null hypothesis when the p-value is less than \(\alpha\) . This is often called “rejecting the null hypothesis at significance level \(\alpha\) ”. More formally, we might write
\[ P(\text{reject} \; H_0 | H_0 \; \text{true}) = \alpha \]
False negatives
On the other hand, we may also fail to reject the null hypothesis when the null hypothesis is in fact false. We might just not have enough data to reject the null, for example. We call this a false negative or a Type II error. We write this as
\[ \text{Power} = P(\text{fail to reject} \; H_0 | H_0 \; \text{false}) = 1 - \beta \]
To achieve a power of \(1 - \beta\) for a one sample Z-test, you need
\[ n \approx \left( { \sigma \cdot (z_{\alpha / 2} + z_\beta) \over \mu_0 - \mu_A } \right)^2 \]
where \(\mu_A\) is the true mean and \(\mu_0\) is the proposed mean. We’ll do an exercise later that will help you see where this comes from.
A company claims battery lifetimes are normally distributed with \(\mu = 40\) and \(\sigma = 5\) hours. We are curious if the claim about the mean is reasonable, and collect a random sample of 100 batteries. The sample mean is 39.8. What is the p-value of a Z-test for \(H_0 : \mu = 40\) ?
We begin by calculating a Z-score
\[ Z = {\bar x - \mu_0 \over {\sigma \over \sqrt n}} = {39.8 - 40 \over {5 \over \sqrt 100}} = 0.4 \]
and then we calculate, using the fact that \(Z \sim \mathrm{Normal}(0, 1)\) ,
\[ P(Z < -0.4) + P(Z > 0.4) \approx 0.69 \]
we might also be interested in a one-sided test, where \(H_A : \mu < 40\) . In this case the p-value is only the case when \(Z < -0.4\) , and the p-value is
\[ P(Z < -0.4) \approx 0.34 \]
Power for Z-test
Suppose a powdered medicine is supposed to have a mean particle diameter of \(\mu = 15\) micrometers, and the standard deviation of diameters stays steady around 1.8 micrometers. The company would like to have high power to detect mean thicknesses 0.2 micrometers away from 15. When \(n = 100\) , what is the power of the test if the true \(\mu\) is 15.2 micrometers. Assume the company is interested in controlling type I error at an \(\alpha = 0.05\) level.
We will reject the null when our Z score is less than \(z_{\alpha / 2}\) or \(z_{1 - \alpha / 2}\) , or when the Z score is less than -1.96 or greater than 1.96. Recall that the Z score is \({\bar x - \mu_0 \over {\sigma \over \sqrt n}}\) , which we can rearrange in terms of \(\bar x\) to see that we will reject the null when \(\bar x < 14.65\) or \(\bar x > 15.35\) .
Now we are interested in the probability of being in this rejection region when the alternative hypothesis \(\mu_A = 15.2\) is true .
\[ P(\bar x > 15.35 | \mu = 15.2) + P(\bar x < 14.65 | \mu = 15.2) \]
and we know that \(\bar x \sim \mathrm{Normal} \left(15.2, 1.8 / \sqrt{100}\right)\) so this equals
\[ 0.001 + 0.198 \approx 0.199 \]
So we have only a power of about 20 percent. This is quite low.
Introduction
- R installation
- Working directory
- Getting help
- Install packages
Data structures
Data Wrangling
- Sort and order
- Merge data frames
Programming
- Creating functions
- If else statement
- apply function
- sapply function
- tapply function
Import & export
- Read TXT files
- Import CSV files
- Read Excel files
- Read SQL databases
- Export data
- plot function
- Scatter plot
- Density plot
- Tutorials Introduction Data wrangling Graphics Statistics See all
HYPOTHESIS TESTING IN R
Hypothesis testing is a statistical procedure used to make decisions or draw conclusions about the characteristics of a population based on information provided by a sample
NORMALITY TESTS
Normality tests are used to evaluate whether a data sample follows a normal distribution. These tests allow to verify if the data have a behavior similar to that of a Gaussian distribution, being useful to determine if the assumptions of certain parametric statistical analyses that require normality in the data are met
Shapiro Wilk normality test
shapiro.test()
Lilliefors normality test
lillie.test()
GOODNESS OF FIT TESTS
These tests are used to verify whether a proposed theoretical distribution adequately matches the observed data. They are useful to assess whether a specific distribution fits the data well, allowing to determine whether a theoretical model accurately represents the observed data distribution
Pearson's Chi-squared test with chisq.test()
chisq.test()
Kolmogorov-Smirnov test with ks.test()
Median tests.
Median tests are used to test whether the medians of two or more groups are statistically different, thus identifying whether there are significant differences in medians between populations or treatments
Wilcoxon signed rank test
wilcox.test()
Wilcoxon rank sum test (Mann-Whitney U test)

Kruskal Wallis rank sum test (H test)
kruskal.test()
OTHER TYPES OF TESTS
There are other types of tests, such as tests for comparing means, for equality of variances or for equality of proportions

T-test to compare means
F test with var.test() to compare two variances

Test for proportions with prop.test()
prop.test()
Try adjusting your search query
👉 If you haven’t found what you’re looking for, consider clicking the checkbox to activate the extended search on R CHARTS for additional graphs tutorials, try searching a synonym of your query if possible (e.g., ‘bar plot’ -> ‘bar chart’), search for a more generic query or if you are searching for a specific function activate the functions search or use the functions search bar .

Quantitative Methods Using R
10 hypothesis testing.
Hypothesis testing is a method used to make decisions about population parameters based on sample data.
10.1 Hypothesis
A hypothesis is an educated guess or statement about the relationship between variables or the characteristics of a population. In hypothesis testing, there are two main hypotheses:
10.1.1 Null hypothesis (H0):
This hypothesis states that there is no effect or no relationship between variables. It is typically the hypothesis that the researcher wants to disprove.
10.1.2 Alternative hypothesis (H1):
This hypothesis states that there is an effect or a relationship between variables. It is the hypothesis that the researcher wants to prove or provide evidence for.
10.2 Decision Type Error
When performing hypothesis testing, there are two types of decision errors:
Type I Error (α): This error occurs when the null hypothesis is rejected when it is actually true. In other words, it’s a false positive. The probability of committing a Type I error is denoted by the significance level (α), which is typically set at 0.05 or 0.01. Type II Error (β): This error occurs when the null hypothesis is not rejected when it is actually false. In other words, it’s a false negative. The probability of committing a Type II error is denoted by β. The power of a test (1 - β) measures the ability of the test to detect an effect when it truly exists. Here is a graphical representation of the types of decision errors:
Hypothesis Testing Errors
This table represents the different outcomes when making decisions based on hypothesis testing. The columns represent the reality (i.e., whether the null hypothesis is true or false), and the rows represent the decision made based on the hypothesis test (i.e., whether to reject or not reject the null hypothesis). The cells show the types of decision errors (Type I and Type II errors) and the correct decisions.
10.3 Level of Signficance
The level of significance is a critical component in hypothesis testing because it sets a threshold for determining whether an observed effect is statistically significant or not.
The level of significance is denoted by the Greek letter α (alpha) and represents the probability of making a Type I error. A Type I error occurs when we reject the null hypothesis (H0) when it is actually true. By choosing a level of significance, researchers define the risk they are willing to take when rejecting a true null hypothesis. Common levels of significance are 0.05 (5%) and 0.01 (1%).
To better understand the role of the level of significance in hypothesis testing, let’s consider the following steps:
Formulate the null hypothesis (H0) and the alternative hypothesis (H1): The null hypothesis typically states that there is no effect or relationship between variables, while the alternative hypothesis states that there is an effect or relationship.
Choose a level of significance (α): Determine the threshold for the probability of making a Type I error. For example, if α is set to 0.05, there is a 5% chance of rejecting a true null hypothesis.
Perform the statistical test and calculate the test statistic: The test statistic is calculated using the sample data, and it helps determine how far the observed sample mean is from the hypothesized population mean. In the case of a single mean, a one-sample t-test is commonly used, and the test statistic is the t-value.
Determine the critical value or p-value: Compare the calculated test statistic with the critical value or the p-value (probability value) to make a decision about the null hypothesis. The critical value is a threshold value that depends on the chosen level of significance and the distribution of the test statistic. The p-value represents the probability of obtaining a test statistic as extreme or more extreme than the observed test statistic under the assumption that the null hypothesis is true.
Make a decision: If the test statistic is more extreme than the critical value, or if the p-value is less than the level of significance (α), reject the null hypothesis. Otherwise, fail to reject the null hypothesis.
10.4 T-statistic
The t-statistic is a standardized measure used in hypothesis testing to compare the observed sample mean with the hypothesized population mean. It takes into account the sample mean, the hypothesized population mean, and the standard error of the mean. Mathematically, the t-statistic can be calculated using the following formula:
t = (X̄ - μ) / (s / √n)
t is the t-statistic X̄ is the sample mean μ is the hypothesized population mean s is the sample standard deviation n is the sample size
10.4.1 T-distribution
The t-distribution, also known as the Student’s t-distribution, is a probability distribution that is used when the population standard deviation is unknown and the sample size is small. It is similar to the normal distribution but has thicker tails, which accounts for the increased variability due to using the sample standard deviation as an estimate of the population standard deviation. The shape of the t-distribution depends on the degrees of freedom (df), which is related to the sample size (df = n - 1). As the sample size increases, the t-distribution approaches the normal distribution.
To calculate the t-statistic in R, you can use the following code:
To perform a one-sample t-test in R, which calculates the t-statistic and p-value automatically, you can use the t.test() function:
10.4.2 Intepreting Normality Evidence
When using a t-test, the assumption of normality is important. The data should follow a normal distribution to ensure the validity of the test results. To assess the normality of the data, we can use visual methods (histograms, Q-Q plots) and statistical tests (e.g., Shapiro-Wilk test).
This is important because the t-test assumes that the data follow a normal distribution, and verifying this assumption helps ensure the validity of the test results.
To generate normality evidence after performing a t-test, you can use the following methods:
Visual methods: Histograms and Q-Q plots can provide a visual assessment of the normality of the data.
Statistical tests: Shapiro-Wilk test and Kolmogorov-Smirnov test are commonly used to test for normality. These tests generate p-values, which can be compared with a chosen significance level (e.g., 0.05) to determine if the data deviate significantly from normality.
In R, you can create a histogram and Q-Q plot using the following code:
- Create a histogram and Q-Q plot:

- Perform the Shapiro-Wilk test:
To interpret the normality evidence, follow these guidelines:
Visual methods: Inspect the histogram and Q-Q plot. If the histogram is roughly bell-shaped and the points on the Q-Q plot fall approximately on the reference line, the data can be considered approximately normally distributed.
Statistical tests: Check the p-values of the normality tests. If the p-value is greater than the chosen significance level (e.g., 0.05), the null hypothesis (i.e., the data follow a normal distribution) cannot be rejected. This suggests that the data do not deviate significantly from normality.
Keep in mind that no single method is foolproof, and it’s often a good idea to use a combination of visual and statistical methods to assess normality. If the data appear to be non-normal, you might consider using non-parametric alternatives to the t-test or transforming the data to achieve normality.
10.5 Statistical Power
Statistical power is the probability of correctly rejecting the null hypothesis when it is false, which means not committing a Type II error. Power is influenced by factors such as sample size, effect size, and the chosen significance level (α). Power analysis helps researchers determine the appropriate sample size needed to achieve a desired level of power, typically 0.8 or higher.
To perform power analysis in R, you can use the pwr package, which provides a set of functions for power calculations in various statistical tests, including the t-test.
Here’s a step-by-step procedure for generating and testing power using R:
- Install and load the pwr package:
- Define the parameters for power analysis. You will need to specify the effect size (Cohen’s d), sample size, and significance level (α):
- Use the pwr.t.test() function to calculate the power for a one-sample t-test:
The output will show the calculated power, sample size, effect size, and significance level. If the power is below the desired level (e.g., 0.8), you can adjust the sample size or effect size and recalculate the power to determine the necessary changes for achieving the desired power level.
It’s essential to consider the practical implications of the effect size and sample size when planning a study. A large effect size may be easier to detect but might not occur frequently in real-world situations. Conversely, a small effect size might be more difficult to detect and may require a larger sample size to achieve adequate power.
An Introduction to Bayesian Thinking
Chapter 5 hypothesis testing with normal populations.
In Section 3.5 , we described how the Bayes factors can be used for hypothesis testing. Now we will use the Bayes factors to compare normal means, i.e., test whether the mean of a population is zero or compare the means of two groups of normally-distributed populations. We divide this mission into three cases: known variance for a single population, unknown variance for a single population using paired data, and unknown variance using two independent groups.
Also note that some of the examples in this section use an updated version of the bayes_inference function. If your local output is different from what is seen in this chapter, or the provided code fails to run for you please make sure that you have the most recent version of the package.
5.1 Bayes Factors for Testing a Normal Mean: variance known
Now we show how to obtain Bayes factors for testing hypothesis about a normal mean, where the variance is known . To start, let’s consider a random sample of observations from a normal population with mean \(\mu\) and pre-specified variance \(\sigma^2\) . We consider testing whether the population mean \(\mu\) is equal to \(m_0\) or not.
Therefore, we can formulate the data and hypotheses as below:
Data \[Y_1, \cdots, Y_n \mathrel{\mathop{\sim}\limits^{\rm iid}}\textsf{Normal}(\mu, \sigma^2)\]
- \(H_1: \mu = m_0\)
- \(H_2: \mu \neq m_0\)
We also need to specify priors for \(\mu\) under both hypotheses. Under \(H_1\) , we assume that \(\mu\) is exactly \(m_0\) , so this occurs with probability 1 under \(H_1\) . Now under \(H_2\) , \(\mu\) is unspecified, so we describe our prior uncertainty with the conjugate normal distribution centered at \(m_0\) and with a variance \(\sigma^2/\mathbf{n_0}\) . This is centered at the hypothesized value \(m_0\) , and it seems that the mean is equally likely to be larger or smaller than \(m_0\) , so a dividing factor \(n_0\) is given to the variance. The hyper parameter \(n_0\) controls the precision of the prior as before.
In mathematical terms, the priors are:
- \(H_1: \mu = m_0 \text{ with probability 1}\)
- \(H_2: \mu \sim \textsf{Normal}(m_0, \sigma^2/\mathbf{n_0})\)
Bayes Factor
Now the Bayes factor for comparing \(H_1\) to \(H_2\) is the ratio of the distribution, the data under the assumption that \(\mu = m_0\) to the distribution of the data under \(H_2\) .
\[\begin{aligned} \textit{BF}[H_1 : H_2] &= \frac{p(\text{data}\mid \mu = m_0, \sigma^2 )} {\int p(\text{data}\mid \mu, \sigma^2) p(\mu \mid m_0, \mathbf{n_0}, \sigma^2)\, d \mu} \\ \textit{BF}[H_1 : H_2] &=\left(\frac{n + \mathbf{n_0}}{\mathbf{n_0}} \right)^{1/2} \exp\left\{-\frac 1 2 \frac{n }{n + \mathbf{n_0}} Z^2 \right\} \\ Z &= \frac{(\bar{Y} - m_0)}{\sigma/\sqrt{n}} \end{aligned}\]
The term in the denominator requires integration to account for the uncertainty in \(\mu\) under \(H_2\) . And it can be shown that the Bayes factor is a function of the observed sampled size, the prior sample size \(n_0\) and a \(Z\) score.
Let’s explore how the hyperparameters in \(n_0\) influences the Bayes factor in Equation (5.1) . For illustration we will use the sample size of 100. Recall that for estimation, we interpreted \(n_0\) as a prior sample size and considered the limiting case where \(n_0\) goes to zero as a non-informative or reference prior.
\[\begin{equation} \textsf{BF}[H_1 : H_2] = \left(\frac{n + \mathbf{n_0}}{\mathbf{n_0}}\right)^{1/2} \exp\left\{-\frac{1}{2} \frac{n }{n + \mathbf{n_0}} Z^2 \right\} \tag{5.1} \end{equation}\]
Figure 5.1 shows the Bayes factor for comparing \(H_1\) to \(H_2\) on the y-axis as \(n_0\) changes on the x-axis. The different lines correspond to different values of the \(Z\) score or how many standard errors \(\bar{y}\) is from the hypothesized mean. As expected, larger values of the \(Z\) score favor \(H_2\) .

Figure 5.1: Vague prior for mu: n=100
But as \(n_0\) becomes smaller and approaches 0, the first term in the Bayes factor goes to infinity, while the exponential term involving the data goes to a constant and is ignored. In the limit as \(n_0 \rightarrow 0\) under this noninformative prior, the Bayes factor paradoxically ends up favoring \(H_1\) regardless of the value of \(\bar{y}\) .
The takeaway from this is that we cannot use improper priors with \(n_0 = 0\) , if we are going to test our hypothesis that \(\mu = n_0\) . Similarly, vague priors that use a small value of \(n_0\) are not recommended due to the sensitivity of the results to the choice of an arbitrarily small value of \(n_0\) .
This problem arises with vague priors – the Bayes factor favors the null model \(H_1\) even when the data are far away from the value under the null – are known as the Bartlett’s paradox or the Jeffrey’s-Lindleys paradox.
Now, one way to understand the effect of prior is through the standard effect size
\[\delta = \frac{\mu - m_0}{\sigma}.\] The prior of the standard effect size is
\[\delta \mid H_2 \sim \textsf{Normal}(0, \frac{1}{\mathbf{n_0}})\]
This allows us to think about a standardized effect independent of the units of the problem. One default choice is using the unit information prior, where the prior sample size \(n_0\) is 1, leading to a standard normal for the standardized effect size. This is depicted with the blue normal density in Figure 5.2 . This suggested that we expect that the mean will be within \(\pm 1.96\) standard deviations of the hypothesized mean with probability 0.95 . (Note that we can say this only under a Bayesian setting.)
In many fields we expect that the effect will be small relative to \(\sigma\) . If we do not expect to see large effects, then we may want to use a more informative prior on the effect size as the density in orange with \(n_0 = 4\) . So they expected the mean to be within \(\pm 1/\sqrt{n_0}\) or five standard deviations of the prior mean.

Figure 5.2: Prior on standard effect size
Example 1.1 To illustrate, we give an example from parapsychological research. The case involved the test of the subject’s claim to affect a series of randomly generated 0’s and 1’s by means of extra sensory perception (ESP). The random sequence of 0’s and 1’s are generated by a machine with probability of generating 1 being 0.5. The subject claims that his ESP would make the sample mean differ significantly from 0.5.
Therefore, we are testing \(H_1: \mu = 0.5\) versus \(H_2: \mu \neq 0.5\) . Let’s use a prior that suggests we do not expect a large effect which leads the following solution for \(n_0\) . Assume we want a standard effect of 0.03, there is a 95% chance that it is between \((-0.03/\sigma, 0.03/\sigma)\) , with \(n_0 = (1.96\sigma/0.03)^2 = 32.7^2\) .
Figure 5.3 shows our informative prior in blue, while the unit information prior is in orange. On this scale, the unit information prior needs to be almost uniform for the range that we are interested.

Figure 5.3: Prior effect in the extra sensory perception test
A very large data set with over 104 million trials was collected to test this hypothesis, so we use a normal distribution to approximate the distribution the sample mean.
- Sample size: \(n = 1.0449 \times 10^8\)
- Sample mean: \(\bar{y} = 0.500177\) , standard deviation \(\sigma = 0.5\)
- \(Z\) -score: 3.61
Now using our prior in the data, the Bayes factor for \(H_1\) to \(H_2\) was 0.46, implying evidence against the hypothesis \(H_1\) that \(\mu = 0.5\) .
- Informative \(\textit{BF}[H_1:H_2] = 0.46\)
- \(\textit{BF}[H_2:H_1] = 1/\textit{BF}[H_1:H_2] = 2.19\)
Now, this can be inverted to provide the evidence in favor of \(H_2\) . The evidence suggests that the hypothesis that the machine operates with a probability that is not 0.5, is 2.19 times more likely than the hypothesis the probability is 0.5. Based on the interpretation of Bayes factors from Table 3.5 , this is in the range of “not worth the bare mention”.
To recap, we present expressions for calculating Bayes factors for a normal model with a specified variance. We show that the improper reference priors for \(\mu\) when \(n_0 = 0\) , or vague priors where \(n_0\) is arbitrarily small, lead to Bayes factors that favor the null hypothesis regardless of the data, and thus should not be used for hypothesis testing.
Bayes factors with normal priors can be sensitive to the choice of the \(n_0\) . While the default value of \(n_0 = 1\) is reasonable in many cases, this may be too non-informative if one expects more effects. Wherever possible, think about how large an effect you expect and use that information to help select the \(n_0\) .
All the ESP examples suggest weak evidence and favored the machine generating random 0’s and 1’s with a probability that is different from 0.5. Note that ESP is not the only explanation – a deviation from 0.5 can also occur if the random number generator is biased. Bias in the stream of random numbers in our pseudorandom numbers has huge implications for numerous fields that depend on simulation. If the context had been about detecting a small bias in random numbers what prior would you use and how would it change the outcome? You can experiment it in R or other software packages that generate random Bernoulli trials.
Next, we will look at Bayes factors in normal models with unknown variances using the Cauchy prior so that results are less sensitive to the choice of \(n_0\) .
5.2 Comparing Two Paired Means using Bayes Factors
We previously learned that we can use a paired t-test to compare means from two paired samples. In this section, we will show how Bayes factors can be expressed as a function of the t-statistic for comparing the means and provide posterior probabilities of the hypothesis that whether the means are equal or different.
Example 5.1 Trace metals in drinking water affect the flavor, and unusually high concentrations can pose a health hazard. Ten pairs of data were taken measuring the zinc concentration in bottom and surface water at ten randomly sampled locations, as listed in Table 5.1 .
Water samples collected at the the same location, on the surface and the bottom, cannot be assumed to be independent of each other. However, it may be reasonable to assume that the differences in the concentration at the bottom and the surface in randomly sampled locations are independent of each other.
| location | bottom | surface | difference |
|---|---|---|---|
| 1 | 0.430 | 0.415 | 0.015 |
| 2 | 0.266 | 0.238 | 0.028 |
| 3 | 0.567 | 0.390 | 0.177 |
| 4 | 0.531 | 0.410 | 0.121 |
| 5 | 0.707 | 0.605 | 0.102 |
| 6 | 0.716 | 0.609 | 0.107 |
| 7 | 0.651 | 0.632 | 0.019 |
| 8 | 0.589 | 0.523 | 0.066 |
| 9 | 0.469 | 0.411 | 0.058 |
| 10 | 0.723 | 0.612 | 0.111 |
To start modeling, we will treat the ten differences as a random sample from a normal population where the parameter of interest is the difference between the average zinc concentration at the bottom and the average zinc concentration at the surface, or the main difference, \(\mu\) .
In mathematical terms, we have
- Random sample of \(n= 10\) differences \(Y_1, \ldots, Y_n\)
- Normal population with mean \(\mu \equiv \mu_B - \mu_S\)
In this case, we have no information about the variability in the data, and we will treat the variance, \(\sigma^2\) , as unknown.
The hypothesis of the main concentration at the surface and bottom are the same is equivalent to saying \(\mu = 0\) . The second hypothesis is that the difference between the mean bottom and surface concentrations, or equivalently that the mean difference \(\mu \neq 0\) .
In other words, we are going to compare the following hypotheses:
- \(H_1: \mu_B = \mu_S \Leftrightarrow \mu = 0\)
- \(H_2: \mu_B \neq \mu_S \Leftrightarrow \mu \neq 0\)
The Bayes factor is the ratio between the distributions of the data under each hypothesis, which does not depend on any unknown parameters.
\[\textit{BF}[H_1 : H_2] = \frac{p(\text{data}\mid H_1)} {p(\text{data}\mid H_2)}\]
To obtain the Bayes factor, we need to use integration over the prior distributions under each hypothesis to obtain those distributions of the data.
\[\textit{BF}[H_1 : H_2] = \iint p(\text{data}\mid \mu, \sigma^2) p(\mu \mid \sigma^2) p(\sigma^2 \mid H_2)\, d \mu \, d\sigma^2\]
This requires specifying the following priors:
- \(\mu \mid \sigma^2, H_2 \sim \textsf{Normal}(0, \sigma^2/n_0)\)
- \(p(\sigma^2) \propto 1/\sigma^2\) for both \(H_1\) and \(H_2\)
\(\mu\) is exactly zero under the hypothesis \(H_1\) . For \(\mu\) in \(H_2\) , we start with the same conjugate normal prior as we used in Section 5.1 – testing the normal mean with known variance. Since we assume that \(\sigma^2\) is known, we model \(\mu \mid \sigma^2\) instead of \(\mu\) itself.
The \(\sigma^2\) appears in both the numerator and denominator of the Bayes factor. For default or reference case, we use the Jeffreys prior (a.k.a. reference prior) on \(\sigma^2\) . As long as we have more than two observations, this (improper) prior will lead to a proper posterior.
After integration and rearranging, one can derive a simple expression for the Bayes factor:
\[\textit{BF}[H_1 : H_2] = \left(\frac{n + n_0}{n_0} \right)^{1/2} \left( \frac{ t^2 \frac{n_0}{n + n_0} + \nu } { t^2 + \nu} \right)^{\frac{\nu + 1}{2}}\]
This is a function of the t-statistic
\[t = \frac{|\bar{Y}|}{s/\sqrt{n}},\]
where \(s\) is the sample standard deviation and the degrees of freedom \(\nu = n-1\) (sample size minus one).
As we saw in the case of Bayes factors with known variance, we cannot use the improper prior on \(\mu\) because when \(n_0 \to 0\) , then \(\textit{BF}[H1:H_2] \to \infty\) favoring \(H_1\) regardless of the magnitude of the t-statistic. Arbitrary, vague small choices for \(n_0\) also lead to arbitrary large Bayes factors in favor of \(H_1\) . Another example of the Barlett’s or Jeffreys-Lindley paradox.
Sir Herald Jeffrey discovered another paradox testing using the conjugant normal prior, known as the information paradox . His thought experiment assumed that our sample size \(n\) and the prior sample size \(n_0\) . He then considered what would happen to the Bayes factor as the sample mean moved further and further away from the hypothesized mean, measured in terms standard errors with the t-statistic, i.e., \(|t| \to \infty\) . As the t-statistic or information about the mean moved further and further from zero, the Bayes factor goes to a constant depending on \(n, n_0\) rather than providing overwhelming support for \(H_2\) .
The bounded Bayes factor is
\[\textit{BF}[H_1 : H_2] \to \left( \frac{n_0}{n_0 + n} \right)^{\frac{n - 1}{2}}\]
Jeffrey wanted a prior with \(\textit{BF}[H_1 : H_2] \to 0\) (or equivalently, \(\textit{BF}[H_2 : H_1] \to \infty\) ), as the information from the t-statistic grows, indicating the sample mean is as far as from the hypothesized mean and should favor \(H_2\) .
To resolve the paradox when the information the t-statistic favors \(H_2\) but the Bayes factor does not, Jeffreys showed that no normal prior could resolve the paradox .
But a Cauchy prior on \(\mu\) , would resolve it. In this way, \(\textit{BF}[H_2 : H_1]\) goes to infinity as the sample mean becomes further away from the hypothesized mean. Recall that the Cauchy prior is written as \(\textsf{C}(0, r^2 \sigma^2)\) . While Jeffreys used a default of \(r = 1\) , smaller values of \(r\) can be used if smaller effects are expected.
The combination of the Jeffrey’s prior on \(\sigma^2\) and this Cauchy prior on \(\mu\) under \(H_2\) is sometimes referred to as the Jeffrey-Zellener-Siow prior .
However, there is no closed form expressions for the Bayes factor under the Cauchy distribution. To obtain the Bayes factor, we must use the numerical integration or simulation methods.
We will use the function from the package to test whether the mean difference is zero in Example 5.1 (zinc), using the JZS (Jeffreys-Zellener-Siow) prior.

With equal prior probabilities on the two hypothesis, the Bayes factor is the posterior odds. From the output, we see this indicates that the hypothesis \(H_2\) , the mean difference is different from 0, is almost 51 times more likely than the hypothesis \(H_1\) that the average concentration is the same at the surface and the bottom.
To sum up, we have used the Cauchy prior as a default prior testing hypothesis about a normal mean when variances are unknown. This does require numerical integration, but it is available in the function from the package. If you expect that the effect sizes will be small, smaller values of \(r\) are recommended.
It is often important to quantify the magnitude of the difference in addition to testing. The Cauchy Prior provides a default prior for both testing and inference; it avoids problems that arise with choosing a value of \(n_0\) (prior sample size) in both cases. In the next section, we will illustrate using the Cauchy prior for comparing two means from independent normal samples.
5.3 Comparing Independent Means: Hypothesis Testing
In the previous section, we described Bayes factors for testing whether the mean difference of paired samples was zero. In this section, we will consider a slightly different problem – we have two independent samples, and we would like to test the hypothesis that the means are different or equal.
Example 5.2 We illustrate the testing of independent groups with data from a 2004 survey of birth records from North Carolina, which are available in the package.
The variable of interest is – the weight gain of mothers during pregnancy. We have two groups defined by the categorical variable, , with levels, younger mom and older mom.
Question of interest : Do the data provide convincing evidence of a difference between the average weight gain of older moms and the average weight gain of younger moms?
We will view the data as a random sample from two populations, older and younger moms. The two groups are modeled as:
\[\begin{equation} \begin{aligned} Y_{O,i} & \mathrel{\mathop{\sim}\limits^{\rm iid}} \textsf{N}(\mu + \alpha/2, \sigma^2) \\ Y_{Y,i} & \mathrel{\mathop{\sim}\limits^{\rm iid}} \textsf{N}(\mu - \alpha/2, \sigma^2) \end{aligned} \tag{5.2} \end{equation}\]
The model for weight gain for older moms using the subscript \(O\) , and it assumes that the observations are independent and identically distributed, with a mean \(\mu+\alpha/2\) and variance \(\sigma^2\) .
For the younger women, the observations with the subscript \(Y\) are independent and identically distributed with a mean \(\mu-\alpha/2\) and variance \(\sigma^2\) .
Using this representation of the means in the two groups, the difference in means simplifies to \(\alpha\) – the parameter of interest.
\[(\mu + \alpha/2) - (\mu - \alpha/2) = \alpha\]
You may ask, “Why don’t we set the average weight gain of older women to \(\mu+\alpha\) , and the average weight gain of younger women to \(\mu\) ?” We need the parameter \(\alpha\) to be present in both \(Y_{O,i}\) (the group of older women) and \(Y_{Y,i}\) (the group of younger women).
We have the following competing hypotheses:
- \(H_1: \alpha = 0 \Leftrightarrow\) The means are not different.
- \(H_2: \alpha \neq 0 \Leftrightarrow\) The means are different.
In this representation, \(\mu\) represents the overall weight gain for all women. (Does the model in Equation (5.2) make more sense now?) To test the hypothesis, we need to specify prior distributions for \(\alpha\) under \(H_2\) (c.f. \(\alpha = 0\) under \(H_1\) ) and priors for \(\mu,\sigma^2\) under both hypotheses.
Recall that the Bayes factor is the ratio of the distribution of the data under the two hypotheses.
\[\begin{aligned} \textit{BF}[H_1 : H_2] &= \frac{p(\text{data}\mid H_1)} {p(\text{data}\mid H_2)} \\ &= \frac{\iint p(\text{data}\mid \alpha = 0,\mu, \sigma^2 )p(\mu, \sigma^2 \mid H_1) \, d\mu \,d\sigma^2} {\int \iint p(\text{data}\mid \alpha, \mu, \sigma^2) p(\alpha \mid \sigma^2) p(\mu, \sigma^2 \mid H_2) \, d \mu \, d\sigma^2 \, d \alpha} \end{aligned}\]
As before, we need to average over uncertainty and the parameters to obtain the unconditional distribution of the data. Now, as in the test about a single mean, we cannot use improper or non-informative priors for \(\alpha\) for testing.
Under \(H_2\) , we use the Cauchy prior for \(\alpha\) , or equivalently, the Cauchy prior on the standardized effect \(\delta\) with the scale of \(r\) :
\[\delta = \alpha/\sigma^2 \sim \textsf{C}(0, r^2)\]
Now, under both \(H_1\) and \(H_2\) , we use the Jeffrey’s reference prior on \(\mu\) and \(\sigma^2\) :
\[p(\mu, \sigma^2) \propto 1/\sigma^2\]
While this is an improper prior on \(\mu\) , this does not suffer from the Bartlett’s-Lindley’s-Jeffreys’ paradox as \(\mu\) is a common parameter in the model in \(H_1\) and \(H_2\) . This is another example of the Jeffreys-Zellner-Siow prior.
As in the single mean case, we will need numerical algorithms to obtain the Bayes factor. Now the following output illustrates testing of Bayes factors, using the Bayes inference function from the package.

We see that the Bayes factor for \(H_1\) to \(H_2\) is about 5.7, with positive support for \(H_1\) that there is no difference in average weight gain between younger and older women. Using equal prior probabilities, the probability that there is a difference in average weight gain between the two groups is about 0.15 given the data. Based on the interpretation of Bayes factors from Table 3.5 , this is in the range of “positive” (between 3 and 20).
To recap, we have illustrated testing hypotheses about population means with two independent samples, using a Cauchy prior on the difference in the means. One assumption that we have made is that the variances are equal in both groups . The case where the variances are unequal is referred to as the Behren-Fisher problem, and this is beyond the scope for this course. In the next section, we will look at another example to put everything together with testing and discuss summarizing results.
5.4 Inference after Testing
In this section, we will work through another example for comparing two means using both hypothesis tests and interval estimates, with an informative prior. We will also illustrate how to adjust the credible interval after testing.
Example 5.3 We will use the North Carolina survey data to examine the relationship between infant birth weight and whether the mother smoked during pregnancy. The response variable, , is the birth weight of the baby in pounds. The categorical variable provides the status of the mother as a smoker or non-smoker.
We would like to answer two questions:
Is there a difference in average birth weight between the two groups?
If there is a difference, how large is the effect?
As before, we need to specify models for the data and priors. We treat the data as a random sample for the two populations, smokers and non-smokers.
The birth weights of babies born to non-smokers, designated by a subgroup \(N\) , are assumed to be independent and identically distributed from a normal distribution with mean \(\mu + \alpha/2\) , as in Section 5.3 .
\[Y_{N,i} \mathrel{\mathop{\sim}\limits^{\rm iid}}\textsf{Normal}(\mu + \alpha/2, \sigma^2)\]
While the birth weights of the babies born to smokers, designated by the subgroup \(S\) , are also assumed to have a normal distribution, but with mean \(\mu - \alpha/2\) .
\[Y_{S,i} \mathrel{\mathop{\sim}\limits^{\rm iid}}\textsf{Normal}(\mu - \alpha/2, \sigma^2)\]
The difference in the average birth weights is the parameter \(\alpha\) , because
\[(\mu + \alpha/2) - (\mu - \alpha/2) = \alpha\] .
The hypotheses that we will test are \(H_1: \alpha = 0\) versus \(H_2: \alpha \ne 0\) .
We will still use the Jeffreys-Zellner-Siow Cauchy prior. However, since we may expect the standardized effect size to not be as strong, we will use a scale of \(r = 0.5\) rather than 1.
Therefore, under \(H_2\) , we have \[\delta = \alpha/\sigma \sim \textsf{C}(0, r^2), \text{ with } r = 0.5.\]
Under both \(H_1\) and \(H_2\) , we will use the reference priors on \(\mu\) and \(\sigma^2\) :
\[\begin{aligned} p(\mu) &\propto 1 \\ p(\sigma^2) &\propto 1/\sigma^2 \end{aligned}\]
The input to the base inference function is similar, but now we will specify that \(r = 0.5\) .

We see that the Bayes factor is 1.44, which weakly favors there being a difference in average birth weights for babies whose mothers are smokers versus mothers who did not smoke. Converting this to a probability, we find that there is about a 60% chance of the average birth weights are different.
While looking at evidence of there being a difference is useful, Bayes factors and posterior probabilities do not convey any information about the magnitude of the effect. Reporting a credible interval or the complete posterior distribution is more relevant for quantifying the magnitude of the effect.
Using the function, we can generate samples from the posterior distribution under \(H_2\) using the option.
The 2.5 and 97.5 percentiles for the difference in the means provide a 95% credible interval of 0.023 to 0.57 pounds for the difference in average birth weight. The MCMC output shows not only summaries about the difference in the mean \(\alpha\) , but the other parameters in the model.
In particular, the Cauchy prior arises by placing a gamma prior on \(n_0\) and the conjugate normal prior. This provides quantiles about \(n_0\) after updating with the current data.
The row labeled effect size is the standardized effect size \(\delta\) , indicating that the effects are indeed small relative to the noise in the data.

Figure 5.4: Estimates of effect under H2
Figure 5.4 shows the posterior density for the difference in means, with the 95% credible interval indicated by the shaded area. Under \(H_2\) , there is a 95% chance that the average birth weight of babies born to non-smokers is 0.023 to 0.57 pounds higher than that of babies born to smokers.
The previous statement assumes that \(H_2\) is true and is a conditional probability statement. In mathematical terms, the statement is equivalent to
\[P(0.023 < \alpha < 0.57 \mid \text{data}, H_2) = 0.95\]
However, we still have quite a bit of uncertainty based on the current data, because given the data, the probability of \(H_2\) being true is 0.59.
\[P(H_2 \mid \text{data}) = 0.59\]
Using the law of total probability, we can compute the probability that \(\mu\) is between 0.023 and 0.57 as below:
\[\begin{aligned} & P(0.023 < \alpha < 0.57 \mid \text{data}) \\ = & P(0.023 < \alpha < 0.57 \mid \text{data}, H_1)P(H_1 \mid \text{data}) + P(0.023 < \alpha < 0.57 \mid \text{data}, H_2)P(H_2 \mid \text{data}) \\ = & I( 0 \text{ in CI }) P(H_1 \mid \text{data}) + 0.95 \times P(H_2 \mid \text{data}) \\ = & 0 \times 0.41 + 0.95 \times 0.59 = 0.5605 \end{aligned}\]
Finally, we get that the probability that \(\alpha\) is in the interval, given the data, averaging over both hypotheses, is roughly 0.56. The unconditional statement is the average birth weight of babies born to nonsmokers is 0.023 to 0.57 pounds higher than that of babies born to smokers with probability 0.56. This adjustment addresses the posterior uncertainty and how likely \(H_2\) is.
To recap, we have illustrated testing, followed by reporting credible intervals, and using a Cauchy prior distribution that assumed smaller standardized effects. After testing, it is common to report credible intervals conditional on \(H_2\) . We also have shown how to adjust the probability of the interval to reflect our posterior uncertainty about \(H_2\) . In the next chapter, we will turn to regression models to incorporate continuous explanatory variables.
An R Introduction to Statistics
- Terms of Use
Hypothesis Testing

In the following tutorials, we demonstrate the procedure of hypothesis testing in R first with the intuitive critical value approach. Then we discuss the popular p-value approach as alternative.
- Lower Tail Test of Population Mean with Known Variance
- Upper Tail Test of Population Mean with Known Variance
- Two-Tailed Test of Population Mean with Known Variance
- Lower Tail Test of Population Mean with Unknown Variance
- Upper Tail Test of Population Mean with Unknown Variance
- Two-Tailed Test of Population Mean with Unknown Variance
- Lower Tail Test of Population Proportion
- Upper Tail Test of Population Proportion
- Two-Tailed Test of Population Proportion
- Elementary Statistics with R
- hypothesis testing
- significance level
- type I error
R Tutorial eBook

R Tutorials
- Combining Vectors
- Vector Arithmetics
- Vector Index
- Numeric Index Vector
- Logical Index Vector
- Named Vector Members
- Matrix Construction
- Named List Members
- Data Frame Column Vector
- Data Frame Column Slice
- Data Frame Row Slice
- Data Import
- Frequency Distribution of Qualitative Data
- Relative Frequency Distribution of Qualitative Data
- Category Statistics
- Frequency Distribution of Quantitative Data
- Relative Frequency Distribution of Quantitative Data
- Cumulative Frequency Distribution
- Cumulative Frequency Graph
- Cumulative Relative Frequency Distribution
- Cumulative Relative Frequency Graph
- Stem-and-Leaf Plot
- Scatter Plot
- Interquartile Range
- Standard Deviation
- Correlation Coefficient
- Central Moment
- Binomial Distribution
- Poisson Distribution
- Continuous Uniform Distribution
- Exponential Distribution
- Normal Distribution
- Chi-squared Distribution
- Student t Distribution
- F Distribution
- Point Estimate of Population Mean
- Interval Estimate of Population Mean with Known Variance
- Interval Estimate of Population Mean with Unknown Variance
- Sampling Size of Population Mean
- Point Estimate of Population Proportion
- Interval Estimate of Population Proportion
- Sampling Size of Population Proportion
- Type II Error in Lower Tail Test of Population Mean with Known Variance
- Type II Error in Upper Tail Test of Population Mean with Known Variance
- Type II Error in Two-Tailed Test of Population Mean with Known Variance
- Type II Error in Lower Tail Test of Population Mean with Unknown Variance
- Type II Error in Upper Tail Test of Population Mean with Unknown Variance
- Type II Error in Two-Tailed Test of Population Mean with Unknown Variance
- Population Mean Between Two Matched Samples
- Population Mean Between Two Independent Samples
- Comparison of Two Population Proportions
- Multinomial Goodness of Fit
- Chi-squared Test of Independence
- Completely Randomized Design
- Randomized Block Design
- Factorial Design
- Wilcoxon Signed-Rank Test
- Mann-Whitney-Wilcoxon Test
- Kruskal-Wallis Test
- Estimated Simple Regression Equation
- Coefficient of Determination
- Significance Test for Linear Regression
- Confidence Interval for Linear Regression
- Prediction Interval for Linear Regression
- Residual Plot
- Standardized Residual
- Normal Probability Plot of Residuals
- Estimated Multiple Regression Equation
- Multiple Coefficient of Determination
- Adjusted Coefficient of Determination
- Significance Test for MLR
- Confidence Interval for MLR
- Prediction Interval for MLR
- Estimated Logistic Regression Equation
- Significance Test for Logistic Regression
- Distance Matrix by GPU
- Hierarchical Cluster Analysis
- Kendall Rank Coefficient
- Significance Test for Kendall's Tau-b
- Support Vector Machine with GPU
- Support Vector Machine with GPU, Part II
- Bayesian Classification with Gaussian Process
- Hierarchical Linear Model
- Installing GPU Packages
Copyright © 2009 - 2024 Chi Yau All Rights Reserved Theme design by styleshout Adaptation by Chi Yau
Normality Test in R
- Printable version
Install required R packages
Load required r packages, import your data into r, check your data, case of large sample sizes, visual methods, normality test.
Many of statistical tests including correlation, regression, t-test, and analysis of variance (ANOVA) assume some certain characteristics about the data. They require the data to follow a normal distribution or Gaussian distribution . These tests are called parametric tests , because their validity depends on the distribution of the data.
Normality and the other assumptions made by these tests should be taken seriously to draw reliable interpretation and conclusions of the research.
Before using a parametric test, we should perform some preleminary tests to make sure that the test assumptions are met. In the situations where the assumptions are violated, non-paramatric tests are recommended.
Here, we’ll describe how to check the normality of the data by visual inspection and by significance tests.
Related Book:
- dplyr for data manipulation
- ggpubr for an easy ggplot2-based data visualization
- Install the latest version from GitHub as follow:
- Or, install from CRAN as follow:
Prepare your data as specified here: Best practices for preparing your data set for R
Save your data in an external .txt tab or .csv files
Import your data into R as follow:
Here, we’ll use the built-in R data set named ToothGrowth .
We start by displaying a random sample of 10 rows using the function sample_n ()[in dplyr package].
Show 10 random rows:
Assess the normality of the data in R
We want to test if the variable len (tooth length) is normally distributed.
If the sample size is large enough (n > 30), we can ignore the distribution of the data and use parametric tests.
The central limit theorem tells us that no matter what distribution things have, the sampling distribution tends to be normal if the sample is large enough (n > 30).
However, to be consistent, normality can be checked by visual inspection [ normal plots (histogram) , Q-Q plot (quantile-quantile plot)] or by significance tests ].
Density plot and Q-Q plot can be used to check normality visually.
- Density plot : the density plot provides a visual judgment about whether the distribution is bell shaped.
- Q-Q plot : Q-Q plot (or quantile-quantile plot) draws the correlation between a given sample and the normal distribution. A 45-degree reference line is also plotted.
It’s also possible to use the function qqPlot () [in car package]:
As all the points fall approximately along this reference line, we can assume normality.
Visual inspection, described in the previous section, is usually unreliable. It’s possible to use a significance test comparing the sample distribution to a normal one in order to ascertain whether data show or not a serious deviation from normality.
There are several methods for normality test such as Kolmogorov-Smirnov (K-S) normality test and Shapiro-Wilk’s test .
The null hypothesis of these tests is that “sample distribution is normal”. If the test is significant , the distribution is non-normal.
Shapiro-Wilk’s method is widely recommended for normality test and it provides better power than K-S. It is based on the correlation between the data and the corresponding normal scores.
Note that, normality test is sensitive to sample size. Small samples most often pass normality tests. Therefore, it’s important to combine visual inspection and significance test in order to take the right decision.
The R function shapiro.test () can be used to perform the Shapiro-Wilk test of normality for one variable (univariate):
From the output, the p-value > 0.05 implying that the distribution of the data are not significantly different from normal distribution. In other words, we can assume the normality.
This analysis has been performed using R software (ver. 3.2.4).
Recommended for You!
Recommended for you.
This section contains best data science and self-development resources to help you on your path.
Coursera - Online Courses and Specialization
Data science.
- Course: Machine Learning: Master the Fundamentals by Standford
- Specialization: Data Science by Johns Hopkins University
- Specialization: Python for Everybody by University of Michigan
- Courses: Build Skills for a Top Job in any Industry by Coursera
- Specialization: Master Machine Learning Fundamentals by University of Washington
- Specialization: Statistics with R by Duke University
- Specialization: Software Development in R by Johns Hopkins University
- Specialization: Genomic Data Science by Johns Hopkins University
Popular Courses Launched in 2020
- Google IT Automation with Python by Google
- AI for Medicine by deeplearning.ai
- Epidemiology in Public Health Practice by Johns Hopkins University
- AWS Fundamentals by Amazon Web Services
Trending Courses
- The Science of Well-Being by Yale University
- Google IT Support Professional by Google
- Python for Everybody by University of Michigan
- IBM Data Science Professional Certificate by IBM
- Business Foundations by University of Pennsylvania
- Introduction to Psychology by Yale University
- Excel Skills for Business by Macquarie University
- Psychological First Aid by Johns Hopkins University
- Graphic Design by Cal Arts
Books - Data Science
- Practical Guide to Cluster Analysis in R by A. Kassambara (Datanovia)
- Practical Guide To Principal Component Methods in R by A. Kassambara (Datanovia)
- Machine Learning Essentials: Practical Guide in R by A. Kassambara (Datanovia)
- R Graphics Essentials for Great Data Visualization by A. Kassambara (Datanovia)
- GGPlot2 Essentials for Great Data Visualization in R by A. Kassambara (Datanovia)
- Network Analysis and Visualization in R by A. Kassambara (Datanovia)
- Practical Statistics in R for Comparing Groups: Numerical Variables by A. Kassambara (Datanovia)
- Inter-Rater Reliability Essentials: Practical Guide in R by A. Kassambara (Datanovia)
- R for Data Science: Import, Tidy, Transform, Visualize, and Model Data by Hadley Wickham & Garrett Grolemund
- Hands-On Machine Learning with Scikit-Learn, Keras, and TensorFlow: Concepts, Tools, and Techniques to Build Intelligent Systems by Aurelien Géron
- Practical Statistics for Data Scientists: 50 Essential Concepts by Peter Bruce & Andrew Bruce
- Hands-On Programming with R: Write Your Own Functions And Simulations by Garrett Grolemund & Hadley Wickham
- An Introduction to Statistical Learning: with Applications in R by Gareth James et al.
- Deep Learning with R by François Chollet & J.J. Allaire
- Deep Learning with Python by François Chollet
by FeedBurner

R news and tutorials contributed by hundreds of R bloggers
Do my data follow a normal distribution a note on the most widely used distribution and how to test for normality in r.
Posted on January 28, 2020 by R on Stats and R in R bloggers | 0 Comments

What is a normal distribution?
Empirical rule, why is the normal distribution so crucial in statistics, density plot, normality test.
The normal distribution is a function that defines how a set of measurements is distributed around the center of these measurements (i.e., the mean). Many natural phenomena in real life can be approximated by a bell-shaped frequency distribution known as the normal distribution or the Gaussian distribution.
The normal distribution is a mount-shaped, unimodal and symmetric distribution where most measurements gather around the mean. Moreover, the further a measure deviates from the mean, the lower the probability of occuring. In this sense, for a given variable, it is common to find values close to the mean, but less and less likely to find values as we move away from the mean. Last but not least, since the normal distribution is symmetric around its mean, extreme values in both tails of the distribution are equivalently unlikely. For instance, given that adult height follows a normal distribution, most adults are close to the average height and extremely short adults occur as infrequently as extremely tall adults.
In this article, the focus is on understanding the normal distribution, the associated empirical rule, its parameters and how to compute \(Z\) scores to find probabilities under the curve (illustrated with examples). As it is a requirement in some statistical tests, we also show 4 complementary methods to test the normality assumption in R.
Data possessing an approximately normal distribution have a definite variation, as expressed by the following empirical rule:
- \(\mu \pm \sigma\) includes approximately 68% of the observations
- \(\mu \pm 2 \cdot \sigma\) includes approximately 95% of the observations
- \(\mu \pm 3 \cdot \sigma\) includes almost all of the observations (99.7% to be more precise)
Normal distribution & empirical rule. Source: Wikipedia
where \(\mu\) and \(\sigma\) correspond to the population mean and population standard deviation, respectively.
The empirical rule is illustred by the following 2 examples. Suppose that the scores of an exam in statistics given to all students in a Belgian university are known to have, approximately, a normal distribution with mean \(\mu = 67\) and standard deviation \(\sigma = 9\) . It can then be deduced that approximately 68% of the scores are between 58 and 76, that approximately 95% of the scores are between 49 and 85, and that almost all of the scores (99.7%) are between 40 and 94. Thus, knowing the mean and the standard deviation gives us a fairly good picture of the distribution of scores. Now suppose that a single university student is randomly selected from those who took the exam. What is the probability that her score will be between 49 and 85? Based on the empirical rule, we find that 0.95 is a reasonable answer to this probability question.
The utility and value of the empirical rule are due to the common occurrence of approximately normal distributions of measurements in nature. For example, IQ, shoe size, height, birth weight, etc. are approximately normally-distributed. You will find that approximately 95% of these measurements will be within \(2\sigma\) of their mean (Wackerly, Mendenhall, and Scheaffer 2014) .
Like many probability distributions, the shape and probabilities of the normal distribution is defined entirely by some parameters. The normal distribution has two parameters: (i) the mean \(\mu\) and (ii) the variance \(\sigma^2\) (i.e., the square of the standard deviation \(\sigma\) ). The mean \(\mu\) locates the center of the distribution, that is, the central tendency of the observations, and the variance \(\sigma^2\) defines the width of the distribution, that is, the spread of the observations.
The mean \(\mu\) can take on any finite value (i.e., \(-\infty ), whereas the variance \(\sigma^2\) can assume any positive finite value (i.e., \(\sigma^2 > 0\) ). The shape of the normal distribution changes based on these two parameters. Since there is an infinite number of combinations of the mean and variance, there is an infinite number of normal distributions, and thus an infinite number of forms.
For instance, see how the shapes of the normal distributions vary when the two parameters change:

As you can see on the second graph, when the variance (or the standard deviation) decreases, the observations are closer to the mean. On the contrary, when the variance (or standard deviation) increases, it is more likely that observations will be further away from the mean.
A random variable \(X\) which follows a normal distribution with a mean of 430 and a variance of 17 is denoted \(X ~ \sim \mathcal{N}(\mu = 430, \sigma^2 = 17)\) .
We have seen that, although different normal distributions have different shapes, all normal distributions have common characteristics:
- They are symmetric, 50% of the population is above the mean and 50% of the population is below the mean
- The mean, median and mode are equal
- The empirical rule detailed earlier is applicable to all normal distributions
Probabilities and standard normal distribution
Probabilities and quantiles for random variables with normal distributions are easily found using R via the functions pnorm() and qnorm() . Probabilities associated with a normal distribution can also be found using this Shiny app . However, before computing probabilities, we need to learn more about the standard normal distribution and the \(Z\) score.
Although there are infinitely many normal distributions (since there is a normal distribution for every combination of mean and variance), we need only one table to find the probabilities under the normal curve: the standard normal distribution . The normal standard distribution is a special case of the normal distribution where the mean is equal to 0 and the variance is equal to 1. A normal random variable \(X\) can always be transformed to a standard normal random variable \(Z\) , a process known as “scaling” or “standardization”, by substracting the mean from the observation, and dividing the result by the standard deviation. Formally:
\[Z = \frac{X – \mu}{\sigma}\]
where \(X\) is the observation, \(\mu\) and \(\sigma\) the mean and standard deviation of the population from which the observation was drawn. So the mean of the standard normal distribution is 0, and its variance is 1, denoted \(Z ~ \sim \mathcal{N}(\mu = 0, \sigma^2 = 1)\) .
From this formula, we see that \(Z\) , referred as standard score or \(Z\) score, allows to see how far away one specific observation is from the mean of all observations, with the distance expressed in standard deviations. In other words, the \(Z\) score corresponds to the number of standard deviations one observation is away from the mean. A positive \(Z\) score means that the specific observation is above the mean, whereas a negative \(Z\) score means that the specific observation is below the mean. \(Z\) scores are often used to compare an individual to her peers, or more generally, a measurement compared to its distribution.
For instance, suppose a student scoring 60 at a statistics exam with the mean score of the class being 40, and scoring 65 at an economics exam with the mean score of the class being 80. Given the “raw” scores, one would say that the student performed better in economics than in statistics. However, taking into consideration her peers, it is clear that the student performed relatively better in statistics than in economics. Computing \(Z\) scores allows to take into consideration all other students (i.e., the entire distribution) and gives a better measure of comparison. Let’s compute the \(Z\) scores for the two exams, assuming that the score for both exams follow a normal distribution with the following parameters:
| Statistics | Economics | ||
|---|---|---|---|
| Mean | 40 | 80 | |
| Standard deviation | 8 | 12.5 | |
| Student’s score | 60 | 65 |
\(Z\) scores for:
- Statistics: \(Z_{stat} = \frac{60 – 40}{11} = 2.5\)
- Economics: \(Z_{econ} = \frac{65 – 80}{12.5} = -1.2\)
On the one hand, the \(Z\) score for the exam in statistics is positive ( \(Z_{stat} = 2.5\) ) which means that she performed better than average. On the other hand, her score for the exam in economics is negative ( \(Z_{econ} = -1.2\) ) which means that she performed worse than average. Below an illustration of her grades in a standard normal distribution for better comparison:

Although the score in economics is better in absolute terms, the score in statistics is actually relatively better when comparing each score within its own distribution.
Furthermore, \(Z\) score also enables to compare observations that would otherwise be impossible because they have different units for example. Suppose you want to compare a salary in € with a weight in kg. Without standardization, there is no way to conclude whether someone is more extreme in terms of her wage or in terms of her weight. Thanks to \(Z\) scores, we can compare two values that were in the first place not comparable to each other.
Final remark regarding the interpretation of a \(Z\) score: a rule of thumb is that an observation with a \(Z\) score between -3 and -2 or between 2 and 3 is considered as a rare value. An observation with a \(Z\) score smaller than -3 or larger than 3 is considered as an extremely rare value. A value with any other \(Z\) score is considered as not rare nor extremely rare.
Areas under the normal distribution in R and by hand
Now that we have covered the \(Z\) score, we are going to use it to determine the area under the curve of a normal distribution.
Note that there are several ways to arrive at the solution in the following exercises. You may therefore use other steps than the ones presented to obtain the same result.
Let \(Z\) denote a normal random variable with mean 0 and standard deviation 1, find \(P(Z > 1)\) .
We actually look for the shaded area in the following figure:

Standard normal distribution: \(P(Z > 1)\)
We look for the probability of \(Z\) being larger than 1 so we set the argument lower.tail = FALSE . The default lower.tail = TRUE would give the result for \(P(Z . Note that \(P(Z = 1) = 0\) so writing \(P(Z > 1)\) or \(P(Z \ge 1)\) is equivalent.
See that the random variable \(Z\) has already a mean of 0 and a standard deviation of 1, so no transformation is required. To find the probabilities by hand, we need to refer to the standard normal distribution table shown below:

Standard normal distribution table (Wackerly, Mendenhall, and Scheaffer 2014) .
From the illustration at the top of the table, we see that the values inside the table correspond to the area under the normal curve above a certain \(z\) . Since we are looking precisely at the probability above \(z = 1\) (since we look for \(P(Z > 1)\) ), we can simply proceed down the first ( \(z\) ) column in the table until \(z = 1.0\) . The probability is 0.1587. Thus, \(P(Z > 1) = 0.1587\) . This is similar to what we found using R, except that values in the table are rounded to 4 digits.
Let \(Z\) denote a normal random variable with mean 0 and standard deviation 1, find \(P(−1 \le Z \le 1)\) .
We are looking for the shaded area in the following figure:

Standard normal distribution: \(P(−1 \le Z \le 1)\)
Note that the arguments by default for the mean and the standard deviation are mean = 0 and sd = 1 . Since this is what we need, we can omit them. 1
For this exercise we proceed by steps:
- The shaded area corresponds to the entire area under the normal curve minus the two white areas in both tails of the curve.
- We know that the normal distribution is symmetric.
- Therefore, the shaded area is the entire area under the curve minus two times the white area in the right tail of the curve, the white area in the right tail of the curve being \(P(Z > 1)\) .
- We also know that the entire area under the normal curve is 1.
- Thus, the shaded area is 1 minus 2 times \(P(Z > 1)\) :
\[P(−1 \le Z \le 1) = 1 – 2 \cdot P(Z > 1) = 1 – 2 \cdot 0.1587 = 0.6826\]
where \(P(Z > 1) = 0.1587\) has been found in the previous exercise.
Let \(Z\) denote a normal random variable with mean 0 and standard deviation 1, find \(P(0 \le Z \le 1.37)\) .

Standard normal distribution: \(P(0 \le Z \le 1.37)\)
Again we proceed by steps for this exercise:
- We know that \(P(Z > 0) = 0.5\) since the entire area under the curve is 1, half of it is 0.5.
- The shaded area is half of the entire area under the curve minus the area from 1.37 to infinity.
- The area under the curve from 1.37 to infinity corresponds to \(P(Z > 1.37)\) .
- Therefore, the shaded area is \(0.5 – P(Z > 1.37)\) .
- To find \(P(Z > 1.37)\) , proceed down the \(z\) column in the table to the entry 1.3 and then across the top of the table to the column labeled .07 to read \(P(Z > 1.37) = .0853\)
\[P(0 \le Z \le 1.37) = P(Z > 0) – P(Z > 1.37) = 0.5 – 0.0853 = 0.4147\]
Recap the example presented in the empirical rule: Suppose that the scores of an exam in statistics given to all students in a Belgian university are known to have a normal distribution with mean \(\mu = 67\) and standard deviation \(\sigma = 9\) . What fraction of the scores lies between 70 and 80?

\(P(70 \le X \le 80)\) where \(X \sim \mathcal{N}(\mu = 67, \sigma^2 = 9^2)\)
Remind that we are looking for \(P(70 \le X \le 80)\) where \(X \sim \mathcal{N}(\mu = 67, \sigma^2 = 9^2)\) . The random variable \(X\) is in its “raw” format, meaning that it has not been standardized yet since the mean is 67 and the variance is \(9^2\) . We thus need to first apply the transformation to standardize the endpoints 70 and 80 with the following formula:
After the standardization, \(x = 70\) becomes (in terms of \(z\) , so in terms of deviation from the mean expressed in standard deviation):
\[z = \frac{70 – 67}{9} = 0.3333\]
and \(x = 80\) becomes:
\[z = \frac{80 – 67}{9} = 1.4444\]
The figure above in terms of \(X\) is now in terms of \(Z\) :

\(P(0.3333 \le Z \le 1.4444)\) where \(Z \sim \mathcal{N}(\mu = 0, \sigma^2 = 1)\)
Finding the probability \(P(0.3333 \le Z \le 1.4444)\) is similar to exercises 1 to 3:
- The shaded area corresponds to the area under the curve from \(z = 0.3333\) to \(z = 1.4444\) .
- In other words, the shaded area is the area under the curve from \(z = 0.3333\) to infinity minus the area under the curve from \(z = 1.4444\) to infinity.
- From the table, \(P(Z > 0.3333) = 0.3707\) and \(P(Z > 1.4444) = 0.0749\)
\[P(0.3333 \le Z \le 1.4444) = P(Z > 0.3333) – P(Z > 1.4444) = 0.3707 – 0.0749 = 0.2958\]
The difference with the probability found using in R comes from the rounding.
To conclude this exercice, we can say that, given that the mean scores is 67 and the standard deviation is 9, 29.58% of the students scored between 70 and 80.
See another example in a context here .
The normal distribution is important for three main reasons:
- Some statistical hypothesis tests assume that the data follow a normal distribution
- The central limit theorem states that, for a large number of observations ( \(n > 30\) ), no matter what is the underlying distribution of the original variable, the distribution of the sample means ( \(\overline{X}_n\) ) and of the sum ( \(S_n = \sum_{i = 1}^n X_i\) ) may be approached by a normal distribution
- Linear and nonlinear regression assume that the residuals are normally-distributed
It is therefore useful to know how to test for normality in R, which is the topic of next sections.
How to test the normality assumption
As mentioned above, some statistical tests require that the data follow a normal distribution, or the result of the test may be flawed.
In this section, we show 4 complementary methods to determine whether your data follow a normal distribution in R.
A histogram displays the spread and shape of a distribution, so it is a good starting point to evaluate normality. Let’s have a look at the histogram of a distribution that we would expect to follow a normal distribution, the height of 1,000 adults in cm:

The normal curve with the corresponding mean and variance has been added to the histogram. The histogram follows the normal curve so the data seems to follow a normal distribution.
Below the minimal code for a histogram in R with the dataset iris :

In {ggplot2} :

Histograms are however not sufficient, particularily in the case of small samples because the number of bins greatly change its appearance. Histograms are not recommended when the number of observations is less than 20 because it does not always correctly illustrate the distribution. See two examples below with dataset of 10 and 12 observations:

Can you tell whether these datasets follow a normal distribution? Suprisingly, both follow a normal distribution!
Density plots also provide a visual judgment about whether the data follow a normal distribution. They are similar to histograms as they also allow to analyze the spread and the shape of the distribution. However, they are a smoothed version of the histogram. Here is the density plot drawn from the dataset on the height of the 12 adults discussed above:

In {ggpubr} :

Since it is hard to test for normality from histograms and density plots only, it is recommended to corroborate these graphs with a QQ-plot. QQ-plot, also known as normality plot, is the third method presented to evaluate normality.
Like histograms and density plots, QQ-plots allow to visually evaluate the normality assumption. Here is the QQ-plot drawn from the dataset on the height of the 12 adults discussed above:

Instead of looking at the spread of the data (as it is the case with histograms and density plots), with QQ-plots we only need to ascertain whether the data points follow the line (sometimes referred as Henry’s line).
If points are close to the reference line and within the confidence bands, the normality assumption can be considered as met. The bigger the deviation between the points and the reference line and the more they lie outside the confidence bands, the less likely that the normality condition is met. The height of these 12 adults seem to follow a normal distribution because all points lie within the confidence bands.
When facing a non-normal distribution as shown by the QQ-plot below (systematic departure from the reference line), the first step is usually to apply the logarithm transformation on the data and recheck to see whether the log-transformed data are normally distributed. Applying the logarithm transformation can be done with the log() function.

Note that QQ-plots are also a convenient way to assess whether residuals from regression analysis follow a normal distribution.
The 3 tools presented above were a visual inspection of the normality. Nonetheless, visual inspection may sometimes be unreliable so it is also possible to formally test whether the data follow a normal distribution with statistical tests. These normality tests compare the distribution of the data to a normal distribution in order to assess whether observations show an important deviation from normality.
The two most common normality tests are Shapiro-Wilk’s test and Kolmogorov-Smirnov test. Both tests have the same hypotheses, that is:
- \(H_0\) : the data follow a normal distribution
- \(H_1\) : the data do not follow a normal distribution
Shapiro-Wilk test is recommended for normality test as it provides better power than Kolmogorov-Smirnov test. 2 In R, the Shapiro-Wilk test of normality can be done with the function shapiro.test() : 3
From the output, we see that the \(p\) -value \(> 0.05\) implying that the data are not significantly different from a normal distribution. In other words, we can assume the normality. This test confirms the QQ-plot which also showed normality (as all points lied within the confidence bands).
It is important to note that, in practice, normality tests are often considered as too conservative in the sense that for large sample size ( \(n > 50\) ), a small deviation from the normality may cause the normality condition to be violated. A normality test is a hypothesis test, so as the sample size increases, their capacity of detecting smaller differences increases. So as the number of observations increases, the Shapiro-Wilk test becomes very sensitive even to a small deviation from normality. As a consequence, it happens that according to the normality test the data do not follow a normal distribution although the departures from the normal distribution are negligible and the data in fact follow a normal distribution. For this reason, it is often the case that the normality condition is verified based on a combination of all methods presented in this article, that is, visual inspections (with histograms and QQ-plots) and a formal inspection (with the Shapiro-Wilk test for instance).
I personally tend to prefer QQ-plots over histograms and normality tests so I do not have to bother about the sample size. This article showed the different methods that are available, your choice will of course depends on the type of your data and the context of your analyses.
Thanks for reading. I hope the article helped you to learn more about the normal distribution and how to test for normality in R. See other articles about statistics or about R .
As always, if you have a statistical question related to the topic covered in this article, please add it as a comment so other readers can benefit from the discussion. If you find a mistake or bug, you can inform me by raising an issue on GitHub . For all other requests, you can contact me here .
Get updates every time a new article is published by subscribing to this blog .
Wackerly, Dennis, William Mendenhall, and Richard L Scheaffer. 2014. Mathematical Statistics with Applications . Cengage Learning.
The argument lower.tail = TRUE is also the default so we could omit it as well. However, for clarity and to make sure I compute the propabilities in the correct side of the curve, I used to keep this argument explicit by writing it. ↩
The Shapiro-Wilk test is based on the correlation between the sample and the corresponding normal scores. ↩
In R, the Kolmogorov-Smirnov test is performed with the function ks.test() . ↩
Copyright © 2022 | MH Corporate basic by MH Themes
Never miss an update! Subscribe to R-bloggers to receive e-mails with the latest R posts. (You will not see this message again.)
Stack Exchange Network
Stack Exchange network consists of 183 Q&A communities including Stack Overflow , the largest, most trusted online community for developers to learn, share their knowledge, and build their careers.
Q&A for work
Connect and share knowledge within a single location that is structured and easy to search.
Calculating p-values and pnorm() in R
I am trying to calculate the p-values of observations by comparing them to the normal distribution in R using pnorm() . I have constructed a random distribution as my background model on which I would like to test the significance of various tests. I know for example, my background normal distribution has a mean of 1 and a standard deviation of 3.
Say I have one test that I would like to test the significance of test1 <- 20 . To obtain the p-value of a specific observation with a value of 20, I can use pnorm(20, mean=1, sd=3) . But what if for the same test, I have 5 repeated observations (technical repeats of the same test) with the values:
These 5 numbers have a mean of 20 and a standard deviation of 5. I could simply combine all of the repeated observed by taking the mean and then comparing to the normal distribution, i.e., pnorm(20, mean=1, sd=3) . But in this case, I am leaving out information, namely the standard deviation of these 5 observations. Is there an alternative way to include both the mean and standard deviation of the 5 observations when calculating the p-value?
The alternative is to calculate 5 p-values for each of the 5 observations of test1 .
But then I have to find a way to combine these p-values, to end with one final p-value to look for significance. I ultimately want to know if test1 is significant.
I've looked into the Fisher method and the Stouffers method, but now I am thinking it may be better to just combine the values up front, rather than combining p-values.
- hypothesis-testing
- normal-distribution
- 1 $\begingroup$ If you want to know if a sample comes from a given probability distribution, you can use a Kolmogorov-Smirnov test: ks.test( c(20,25,15,20,15), pnorm, mean=1, sd=3 ) $\endgroup$ – Vincent Zoonekynd Mar 1, 2012 at 5:25
- $\begingroup$ I see - I had not thought about it along these lines...will give it a shot and then respond back. $\endgroup$ – Bryan Mar 1, 2012 at 15:09
- $\begingroup$ Does this test make sense if I only have beetween 4 and 9 numbers in my sample that I will be comparing to the normal dist? thanks! $\endgroup$ – Bryan Mar 1, 2012 at 15:15
- $\begingroup$ test1.rep1 <- 20; test1.rep1 <- 25; test1.rep1 <- 15; test1.rep1 <- 20; test1.rep1 <- 15 "These 5 numbers have a mean of 20 and a sd of 5" I just don't see how the mean works out to be $20$ since $(20+25+15+20+15)/5 = 95/5 = 19$ and the standard deviation is not $5$ either regardless of whether the mean is taken as $20$ or $19$. $\endgroup$ – Dilip Sarwate Mar 1, 2012 at 18:54
- $\begingroup$ I think that's a typo. If you look slightly lower down, he lists his numbers as {20, 25, 15, 25, 15}, these have mean=20 & SD=5, and are identical to the above except that in the upper version the 4th value is 20 instead of 25. $\endgroup$ – gung - Reinstate Monica Mar 1, 2012 at 21:00
You could use Fisher's method of combining p-values, but it wouldn't be the preferred approach. What you want to do here is a t-test , specifically the one-sample version. In R the function is t.test() . Here is a quick tutorial I found by Googling. The way this works is that you are just checking to see if your sample came from a population with a given mean. In your case you want to know what the probability of getting a sample as extreme or more extreme as yours if they were drawn from a population with a mean of 1. It's true that you want to take into account that your sample has a SD of 5. We estimate the standard error of the sampling distribution of the mean by dividing the SD by the square root of N. So, in your case, that would be $2.2=5/\sqrt{5}$.
Now, I should say here that your question taken literally (i.e., as stated) is about a $z$-test, not a $t$-test. That's because you stipulate that you know both the population mean and SD. I think this is the way you asked the question for the sake of understanding the issues (i.e., you wanted a well-defined problem). In practice, this just doesn't really happen. However, if that exact situation is really what you care about, then you would calculate the standard error of the mean by dividing the known SD by the square root of the number of data in your sample. That is $SE = 5/\sqrt 3$, and thus your $SE = 1.3$. Your $z$-score is $14$, and $p < .001$. Here is the R code for that:
Your Answer
Sign up or log in, post as a guest.
Required, but never shown
By clicking “Post Your Answer”, you agree to our terms of service and acknowledge you have read our privacy policy .
Not the answer you're looking for? Browse other questions tagged r hypothesis-testing normal-distribution or ask your own question .
Hot network questions.
- Group with a translation invariant ultrafilter
- In the Unabomber case, was "call Nathan R" really mistakenly written by a New York Times intern?
- Am I seeing double? What kind of helicopter is this, and how many blades does it actually have?
- What's the difference between cryogenic and Liquid propellant?
- Why aren't tightly stitched commercial pcbs more common?
- Sum of square roots (as an algebraic number)
- Is it possible to convert a Bézier curve to a NURBS curve while preserving the curve?
- Mismatching Euler characteristic of the Torus
- I am international anyway
- Why are only projective measurements considered in nonlocal games to get optimal strategy?
- Why is array access not an infix operator?
- Is cellulose, blown-in insulation biodegradeable?
- My players think they found a loophole that gives them infinite poison and XP. How can I add the proper challenges to slow them down?
- Word for a country declaring independence from an empire
- 70s or 80s film or TV show with a handgun that fires backwards and a torture chamber that burns the skin off and chars the victims black
- Cryptic Clue Explanation: Tree that's sported to keep visitors out at university (3)
- Draw Memory Map/Layout/Region in TikZ
- Calculus: Integral of a function
- Why are ETFs so bad at tracking Japanese indices?
- Do reflective warning triangles blow away in wind storms?
- What did the old woman say in "73 Yards"?
- Can you use the special use features with tools without the tool?
- How to make Bash remove quotes after parameter expansion?
- What is the origin of the idiom "say the word"?
Stats and R
Hypothesis test by hand.
- Confidence interval
Hypothesis test
- Inferential statistics
Descriptive versus inferential statistics
Motivations and limitations, step #1: stating the null and alternative hypothesis, step #2: computing the test statistic, step #3: finding the critical value, why don’t we accept \(h_0\) , step #3: computing the p -value, step #4: concluding and interpreting the results, step #2: computing the confidence interval, step #3: concluding and interpreting the results, which method to choose.

Remember that descriptive statistics is the branch of statistics aiming at describing and summarizing a set of data in the best possible manner, that is, by reducing it down to a few meaningful key measures and visualizations—with as little loss of information as possible. In other words, the branch of descriptive statistics helps to have a better understanding and a clear image about a set of observations thanks to summary statistics and graphics. With descriptive statistics, there is no uncertainty because we describe only the group of observations that we decided to work on and no attempt is made to generalize the observed characteristics to another or to a larger group of observations.
Inferential statistics , one the other hand, is the branch of statistics that uses a random sample of data taken from a population to make inferences, i.e., to draw conclusions about the population of interest (see the difference between population and sample if you need a refresh of the two concepts). In other words, information from the sample is used to make generalizations about the parameter of interest in the population.
The two most important tools used in the domain of inferential statistics are:
- hypothesis test (which is the main subject of the present article), and
- confidence interval (which is briefly discussed in this section )
Via my teaching tasks, I realized that many students (especially in introductory statistic classes) struggle to perform hypothesis tests and interpret the results. It seems to me that these students often encounter difficulties mainly because hypothesis testing is rather unclear and abstract to them.
One of the reason it looks abstract to them is because they do not understand the final goal of hypothesis testing—the “why” behind this tool. They often do inferential statistics without understanding the reasoning behind it, as if they were following a cooking recipe which does not require any thinking. However, as soon as they understand the principle underlying hypothesis testing, it is much easier for them to apply the concepts and solve the exercises.
For this reason, I though it would be useful to write an article on the goal of hypothesis tests (the “why?”), in which context they should be used (the “when?”), how they work (the “how?”) and how to interpret the results (the “so what?”). Like anything else in statistics, it becomes much easier to apply a concept in practice when we understand what we are testing or what we are trying to demonstrate beforehand.
In this article, I present—as comprehensibly as possible—the different steps required to perform and conclude a hypothesis test by hand .
These steps are illustrated with a basic example. This will build the theoretical foundations of hypothesis testing, which will in turn be of great help for the understanding of most statistical tests .
Hypothesis tests come in many forms and can be used for many parameters or research questions. The steps I present in this article are not applicable to all hypothesis test, unfortunately.
They are however, appropriate for at least the most common hypothesis tests—the tests on:
- One mean: \(\mu\)
- independent samples: \(\mu_1\) and \(\mu_2\)
- paired samples: \(\mu_D\)
- One proportion: \(p\)
- Two proportions: \(p_1\) and \(p_2\)
- One variance: \(\sigma^2\)
- Two variances: \(\sigma^2_1\) and \(\sigma^2_2\)
The good news is that the principles behind these 6 statistical tests (and many more) are exactly the same. So if you understand the intuition and the process for one of them, all others pretty much follow.
Unlike descriptive statistics where we only describe the data at hand, hypothesis tests use a subset of observations , referred as a sample , to draw conclusions about a population .
One may wonder why we would try to “guess” or make inference about a parameter of a population based on a sample, instead of simply collecting data for the entire population, compute statistics we are interested in and take decisions based upon that.
The main reason we actually use a sample instead of the entire population is because, most of the time, collecting data on the entire population is practically impossible, too complex, too expensive, it would take too long, or a combination of any of these. 1
So the overall objective of a hypothesis test is to draw conclusions in order to confirm or refute a belief about a population , based on a smaller group of observations.
In practice, we take some measurements of the variable of interest—representing the sample(s)—and we check whether our measurements are likely or not given our assumption (our belief). Based on the probability of observing the sample(s) we have, we decide whether we can trust our belief or not.
Hypothesis tests have many practical applications.
Here are different situations illustrating when the 6 tests mentioned above would be appropriate:
- One mean: suppose that a health professional would like to test whether the mean weight of Belgian adults is different than 80 kg (176.4 lbs).
- Independent samples: suppose that a physiotherapist would like to test the effectiveness of a new treatment by measuring the mean response time (in seconds) for patients in a control group and patients in a treatment group, where patients in the two groups are different.
- Paired samples: suppose that a physiotherapist would like to test the effectiveness of a new treatment by measuring the mean response time (in seconds) before and after a treatment, where patients are measured twice—before and after treatment, so patients are the same in the 2 samples.
- One proportion: suppose that a political pundit would like to test whether the proportion of citizens who are going to vote for a specific candidate is smaller than 30%.
- Two proportions: suppose that a doctor would like to test whether the proportion of smokers is different between professional and amateur athletes.
- One variance: suppose that an engineer would like to test whether a voltmeter has a lower variability than what is imposed by the safety standards.
- Two variances: suppose that, in a factory, two production lines work independently from each other. The financial manager would like to test whether the costs of the weekly maintenance of these two machines have the same variance. Note that a test on two variances is also often performed to verify the assumption of equal variances, which is required for several other statistical tests, such as the Student’s t-test for instance.
Of course, this is a non-exhaustive list of potential applications and many research questions can be answered thanks to a hypothesis test.
One important point to remember is that in hypothesis testing we are always interested in the population and not in the sample. The sample is used for the aim of drawing conclusions about the population, so we always test in terms of the population.
Usually, hypothesis tests are used to answer research questions in confirmatory analyses . Confirmatory analyses refer to statistical analyses where hypotheses—deducted from theory—are defined beforehand (preferably before data collection). In this approach, the researcher has a specific idea about the variables under consideration and she is trying to see if her idea, specified as hypotheses, is supported by data.
On the other hand, hypothesis tests are rarely used in exploratory analyses. 2 Exploratory analyses aims to uncover possible relationships between the variables under investigation. In this approach, the researcher does not have any clear theory-driven assumptions or ideas in mind before data collection. This is the reason exploratory analyses are sometimes referred as hypothesis-generating analyses—they are used to create some hypotheses, which in turn may be tested via confirmatory analyses at a later stage.
There are, to my knowledge, 3 different methods to perform a hypothesis tests:
Method A: Comparing the test statistic with the critical value
Method b: comparing the p -value with the significance level \(\alpha\), method c: comparing the target parameter with the confidence interval.
Although the process for these 3 approaches may slightly differ, they all lead to the exact same conclusions. Using one method or another is, therefore, more often than not a matter of personal choice or a matter of context. See this section to know which method I use depending on the context.
I present the 3 methods in the following sections, starting with, in my opinion, the most comprehensive one when it comes to doing it by hand: comparing the test statistic with the critical value.
For the three methods, I will explain the required steps to perform a hypothesis test from a general point of view and illustrate them with the following situation: 3
Suppose a health professional who would like to test whether the mean weight of Belgian adults is different than 80 kg.
Note that, as for most hypothesis tests, the test we are going to use as example below requires some assumptions. Since the aim of the present article is to explain a hypothesis test, we assume that all assumptions are met. For the interested reader, see the assumptions (and how to verify them) for this type of hypothesis test in the article presenting the one-sample t-test .
Method A, which consists in comparing the test statistic with the critical value, boils down to the following 4 steps:
- Stating the null and alternative hypothesis
- Computing the test statistic
- Finding the critical value
- Concluding and interpreting the results
Each step is detailed below.
As discussed before, a hypothesis test first requires an idea, that is, an assumption about a phenomenon. This assumption, referred as hypothesis, is derived from the theory and/or the research question.
Since a hypothesis test is used to confirm or refute a prior belief, we need to formulate our belief so that there is a null and an alternative hypothesis . Those hypotheses must be mutually exclusive , which means that they cannot be true at the same time. This is step #1.
In the context of our scenario, the null and alternative hypothesis are thus:
- Null hypothesis \(H_0: \mu = 80\)
- Alternative hypothesis \(H_1: \mu \ne 80\)
When stating the null and alternative hypothesis, bear in mind the following three points:
- We are always interested in the population and not in the sample. This is the reason \(H_0\) and \(H_1\) will always be written in terms of the population and not in terms of the sample (in this case, \(\mu\) and not \(\bar{x}\) ).
- The assumption we would like to test is often the alternative hypothesis. If the researcher wanted to test whether the mean weight of Belgian adults was less than 80 kg, she would have stated \(H_0: \mu = 80\) (or equivalently, \(H_0: \mu \ge 80\) ) and \(H_1: \mu < 80\) . 4 Do not mix the null with the alternative hypothesis, or the conclusions will be diametrically opposed!
- The null hypothesis is often the status quo. For instance, suppose that a doctor wants to test whether the new treatment A is more efficient than the old treatment B. The status quo is that the new and old treatments are equally efficient. Assuming a larger value is better, she will then write \(H_0: \mu_A = \mu_B\) (or equivalently, \(H_0: \mu_A - \mu_B = 0\) ) and \(H_1: \mu_A > \mu_B\) (or equivalently, \(H_0: \mu_A - \mu_B > 0\) ). On the opposite, if the lower the better, she would have written \(H_0: \mu_A = \mu_B\) (or equivalently, \(H_0: \mu_A - \mu_B = 0\) ) and \(H_1: \mu_A < \mu_B\) (or equivalently, \(H_0: \mu_A - \mu_B < 0\) ).
The test statistic (often called t-stat ) is, in some sense, a metric indicating how extreme the observations are compared to the null hypothesis . The higher the t-stat (in absolute value), the more extreme the observations are.
There are several formulas to compute the t-stat, with one formula for each type of hypothesis test—one or two means, one or two proportions, one or two variances. This means that there is a formula to compute the t-stat for a hypothesis test on one mean, another formula for a test on two means, another for a test on one proportion, etc. 5
The only difficulty in this second step is to choose the appropriate formula. As soon as you know which formula to use based on the type of test, you simply have to apply it to the data. For the interested reader, see the different formulas to compute the t-stat for the most common tests in this Shiny app .
Luckily, formulas for hypothesis tests on one and two means, and one and two proportions follow the same structure.
Computing the test statistic for these tests is similar than scaling a random variable (a process also knows as “standardization” or “normalization”) which consists in subtracting the mean from that random variable, and dividing the result by the standard deviation:
\[Z = \frac{X - \mu}{\sigma}\]
For these 4 hypothesis tests (one/two means and one/two proportions), computing the test statistic is like scaling the estimator (computed from the sample) corresponding to the parameter of interest (in the population). So we basically subtract the target parameter from the point estimator and then divide the result by the standard error (which is equivalent to the standard deviation but for an estimator).
If this is unclear, here is how the test statistic (denoted \(t_{obs}\) ) is computed in our scenario (assuming that the variance of the population is unknown):
\[t_{obs} = \frac{\bar{x} - \mu}{\frac{s}{\sqrt{n}}}\]
- \(\bar{x}\) is the sample mean (i.e., the estimator)
- \(\mu\) is the mean under the null hypothesis (i.e., the target parameter)
- \(s\) is the sample standard deviation
- \(n\) is the sample size
- ( \(\frac{s}{\sqrt{n}}\) is the standard error)
Notice the similarity between the formula of this test statistic and the formula used to standardize a random variable. This structure is the same for a test on two means, one proportion and two proportions, except that the estimator, the parameter and the standard error are, of course, slightly different for each type of test.
Suppose that in our case we have a sample mean of 71 kg ( \(\bar{x}\) = 71), a sample standard deviation of 13 kg ( \(s\) = 13) and a sample size of 10 adults ( \(n\) = 10). Remember that the population mean (the mean under the null hypothesis) is 80 kg ( \(\mu\) = 80).
The t-stat is thus:
\[t_{obs} = \frac{\bar{x} - \mu}{\frac{s}{\sqrt{n}}} = \frac{71 - 80}{\frac{13}{\sqrt{10}}} = -2.189\]
Although formulas are different depending on which parameter you are testing, the value found for the test statistic gives us an indication on how extreme our observations are.
We keep this value of -2.189 in mind because it will be used again in step #4.
Although the t-stat gives us an indication of how extreme our observations are, we cannot tell whether this “score of extremity” is too extreme or not based on its value only.
So, at this point, we cannot yet tell whether our data are too extreme or not. For this, we need to compare our t-stat with a threshold—referred as critical value —given by the probability distribution tables (and which can, of course, also be found with R).
In the same way that the formula to compute the t-stat is different for each parameter of interest, the underlying probability distribution—and thus the statistical table—on which the critical value is based is also different for each target parameter. This means that, in addition to choosing the appropriate formula to compute the t-stat, we also need to select the appropriate probability distribution depending on the parameter we are testing.
Luckily, there are only 4 different probability distributions for the 6 hypothesis tests covered in this article (one/two means, one/two proportions and one/two variances):
- test on one and two means with known population variance(s)
- test on two paired samples where the variance of the difference between the 2 samples \(\sigma^2_D\) is known
- test on one and two proportions (given that some assumptions are met)
- test on one and two means with un known population variance(s)
- test on two paired samples where the variance of the difference between the 2 samples \(\sigma^2_D\) is un known
- test on one variance
- test on two variances
Each probability distribution also has its own parameters (up to two parameters for the 4 distribution considered here), defining its shape and/or location. Parameter(s) of a probability distribution can be seen as its DNA; meaning that the distribution is entirely defined by its parameter(s).
Taking our initial scenario—a health professional who would like to test whether the mean weight of Belgian adults is different than 80 kg—as example.
The underlying probability distribution of a test on one mean is either the standard Normal or the Student distribution, depending on whether the variance of the population (not sample variance!) is known or unknown: 6
- If the population variance is known \(\rightarrow\) the standard Normal distribution is used
- If the population variance is un known \(\rightarrow\) the Student distribution is used
If no population variance is explicitly given, you can assume that it is unknown since you cannot compute it based on a sample. If you could compute it, that would mean you have access to the entire population and there is, in this case, no point in performing a hypothesis test (you could simply use some descriptive statistics to confirm or refute your belief).
In our example, no population variance is specified so it is assumed to be unknown. We therefore use the Student distribution.
The Student distribution has one parameter which defines it; the number of degrees of freedom. The number of degrees of freedom depends on the type of hypothesis test. For instance, the number of degrees of freedom for a test on one mean is equal to the number of observations minus one ( \(n\) - 1). Without going too far into the details, the - 1 comes from the fact that there is one quantity which is estimated (i.e., the mean). 7 The sample size being equal to 10 in our example, the degrees of freedom is equal to \(n\) - 1 = 10 - 1 = 9.
There is only one last element missing to find the critical value: the significance level . The significance level , denoted \(\alpha\) , is the probability of wrongly rejecting the null hypothesis, so the probability of rejecting the null hypothesis although it is in reality true . In this sense, it is an error (type I error, as opposed to the type II error 8 ) that we accept to deal with, in order to be able to draw conclusions about a population based on a subset of it.
As you may have read in many statistical textbooks, the significance level is very often set to 5%. 9 In some fields (such as medicine or engineering, among others), the significance level is also sometimes set to 1% to decrease the error rate.
It is best to specify the significance level before performing a hypothesis test to avoid the temptation to set the significance level in accordance to the results (the temptation is even bigger when the results are on the edge of being significant). As I always tell my students, you cannot “guess” nor compute the significance level. Therefore, if it is not explicitly specified, you can safely assume it is 5%. In our case, we did not indicate it, so we take \(\alpha\) = 5% = 0.05.
Furthermore, in our example, we want to test whether the mean weight of Belgian adults is different than 80 kg. Since we do not specify the direction of the test, it is a two-sided test . If we wanted to test that the mean weight was less than 80 kg ( \(H_1: \mu <\) 80) or greater than 80 kg ( \(H_1: \mu >\) 80), we would have done a one-sided test.
Make sure that you perform the correct test (two-sided or one-sided) because it has an impact on how to find the critical value (see more in the following paragraphs).
So now that we know the appropriate distribution (Student distribution), its parameter (degrees of freedom (df) = 9), the significance level ( \(\alpha\) = 0.05) and the direction (two-sided), we have all we need to find the critical value in the statistical tables :
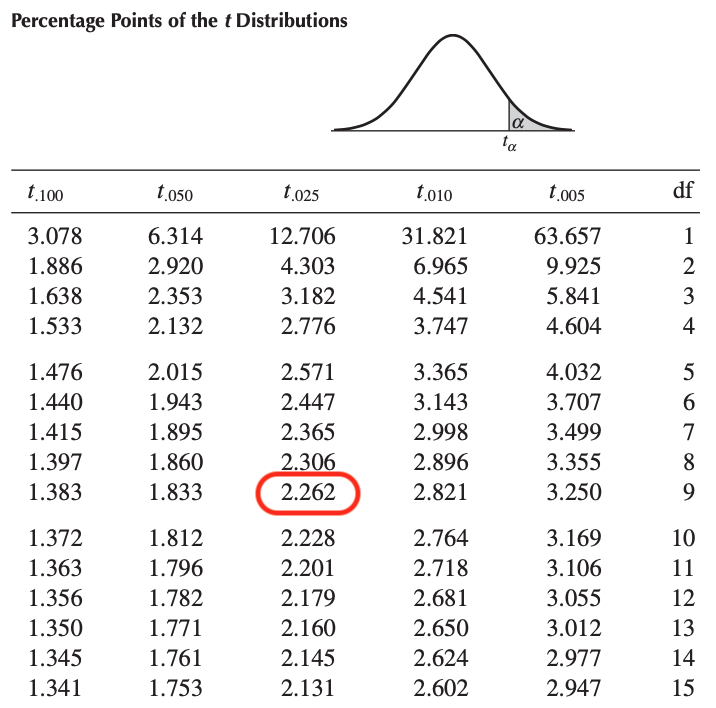
By looking at the row df = 9 and the column \(t_.025\) in the Student’s distribution table, we find a critical value of:
\[t_{n-1; \alpha / 2} = t_{9; 0.025} = 2.262\]
One may wonder why we take \(t_{\alpha/2} = t_.025\) and not \(t_\alpha = t_.05\) since the significance level is 0.05. The reason is that we are doing a two-sided test ( \(H_1: \mu \ne\) 80), so the error rate of 0.05 must be divided in 2 to find the critical value to the right of the distribution. Since the Student’s distribution is symmetric, the critical value to the left of the distribution is simply: -2.262.
Visually, the error rate of 0.05 is partitioned into two parts:
- 0.025 to the left of -2.262 and
- 0.025 to the right of 2.262
We keep in mind these critical values of -2.262 and 2.262 for the fourth and last step.
Note that the red shaded areas in the previous plot are also known as the rejection regions. More on that in the following section.
These critical values can also be found in R, thanks to the qt() function:
The qt() function is used for the Student’s distribution ( q stands for quantile and t for Student). There are other functions accompanying the different distributions:
- qnorm() for the Normal distribution
- qchisq() for the Chi-square distribution
- qf() for the Fisher distribution
In this fourth and last step, all we have to do is to compare the test statistic (computed in step #2) with the critical values (found in step #3) in order to conclude the hypothesis test .
The only two possibilities when concluding a hypothesis test are:
- Rejection of the null hypothesis
- Non-rejection of the null hypothesis
In our example of adult weight, remember that:
- the t-stat is -2.189
- the critical values are -2.262 and 2.262
Also remember that:
- the t-stat gives an indication on how extreme our sample is compared to the null hypothesis
- the critical values are the threshold from which the t-stat is considered as too extreme
To compare the t-stat with the critical values, I always recommend to plot them:
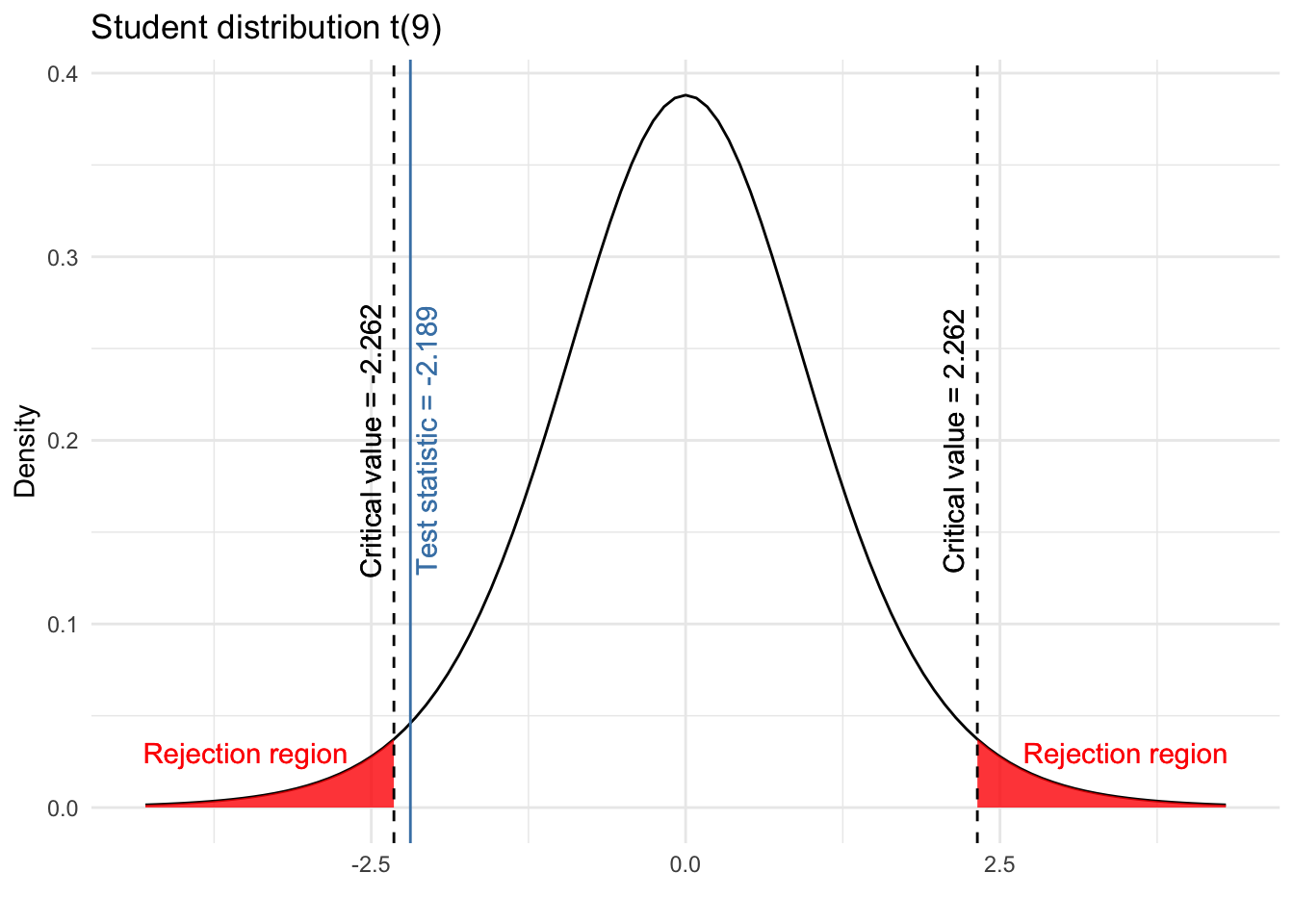
These two critical values form the rejection regions (the red shaded areas):
- from \(- \infty\) to -2.262, and
- from 2.262 to \(\infty\)
If the t-stat lies within one of the rejection region, we reject the null hypothesis . On the contrary, if the t-stat does not lie within any of the rejection region, we do not reject the null hypothesis .
As we can see from the above plot, the t-stat is less extreme than the critical value and therefore does not lie within any of the rejection region. In conclusion, we do not reject the null hypothesis that \(\mu = 80\) .
This is the conclusion in statistical terms but they are meaningless without proper interpretation. So it is a good practice to also interpret the result in the context of the problem:
At the 5% significance level, we do not reject the hypothesis that the mean weight of Belgian adults is 80 kg.
From a more philosophical (but still very important) perspective, note that we wrote “we do not reject the null hypothesis” and “we do not reject the hypothesis that the mean weight of Belgian adults is equal to 80 kg”. We did not write “we accept the null hypothesis” nor “the mean weight of Belgian adults is 80 kg”.
The reason is due to the fact that, in hypothesis testing, we conclude something about the population based on a sample. There is, therefore, always some uncertainty and we cannot be 100% sure that our conclusion is correct.
Perhaps it is the case that the mean weight of Belgian adults is in reality different than 80 kg, but we failed to prove it based on the data at hand. It may be the case that if we had more observations, we would have rejected the null hypothesis (since all else being equal, a larger sample size implies a more extreme t-stat). Or, it may be the case that even with more observations, we would not have rejected the null hypothesis because the mean weight of Belgian adults is in reality close to 80 kg. We cannot distinguish between the two.
So we can just say that we did not find enough evidence against the hypothesis that the mean weight of Belgian adults is 80 kg, but we do not conclude that the mean is equal to 80 kg.
If the difference is still not clear to you, the following example may help. Suppose a person is suspected of having committed a crime. This person is either innocent—the null hypothesis—or guilty—the alternative hypothesis. In the attempt to know if the suspect committed the crime, the police collects as much information and proof as possible. This is similar to the researcher collecting data to form a sample. And then the judge, based on the collected evidence, decides whether the suspect is considered as innocent or guilty. If there is enough evidence that the suspect committed the crime, the judge will conclude that the suspect is guilty. In other words, she will reject the null hypothesis of the suspect being innocent because there are enough evidence that the suspect committed the crime.
This is similar to the t-stat being more extreme than the critical value: we have enough information (based on the sample) to say that the null hypothesis is unlikely because our data would be too extreme if the null hypothesis were true. Since the sample cannot be “wrong” (it corresponds to the collected data), the only remaining possibility is that the null hypothesis is in fact wrong. This is the reason we write “we reject the null hypothesis”.
On the other hand, if there is not enough evidence that the suspect committed the crime (or no evidence at all), the judge will conclude that the suspect is considered as not guilty. In other words, she will not reject the null hypothesis of the suspect being innocent. But even if she concludes that the suspect is considered as not guilty, she will never be 100% sure that he is really innocent.
It may be the case that:
- the suspect did not commit the crime, or
- the suspect committed the crime but the police was not able to collect enough information against the suspect.
In the former case the suspect is really innocent, whereas in the latter case the suspect is guilty but the police and the judge failed to prove it because they failed to find enough evidence against him. Similar to hypothesis testing, the judge has to conclude the case by considering the suspect not guilty, without being able to distinguish between the two.
This is the main reason we write “we do not reject the null hypothesis” or “we fail to reject the null hypothesis” (you may even read in some textbooks conclusion such as “there is no sufficient evidence in the data to reject the null hypothesis”), and we do not write “we accept the null hypothesis”.
I hope this metaphor helped you to understand the reason why we reject the null hypothesis instead of accepting it.
In the following sections, we present two other methods used in hypothesis testing.
These methods will result in the exact same conclusion: non-rejection of the null hypothesis, that is, we do not reject the hypothesis that the mean weight of Belgian adults is 80 kg. It is thus presented only if you prefer to use these methods over the first one.
Method B, which consists in computing the p -value and comparing this p -value with the significance level \(\alpha\) , boils down to the following 4 steps:
- Computing the p -value
In this second method which uses the p -value, the first and second steps are similar than in the first method.
The null and alternative hypotheses remain the same:
- \(H_0: \mu = 80\)
- \(H_1: \mu \ne 80\)
Remember that the formula for the t-stat is different depending on the type of hypothesis test (one or two means, one or two proportions, one or two variances). In our case of one mean with unknown variance, we have:
The p -value is the probability (so it goes from 0 to 1) of observing a sample at least as extreme as the one we observed if the null hypothesis were true. In some sense, it gives you an indication on how likely your null hypothesis is . It is also defined as the smallest level of significance for which the data indicate rejection of the null hypothesis.
For more information about the p -value, I recommend reading this note about the p -value and the significance level \(\alpha\) .
Formally, the p -value is the area beyond the test statistic. Since we are doing a two-sided test, the p -value is thus the sum of the area above 2.189 and below -2.189.
Visually, the p -value is the sum of the two blue shaded areas in the following plot:
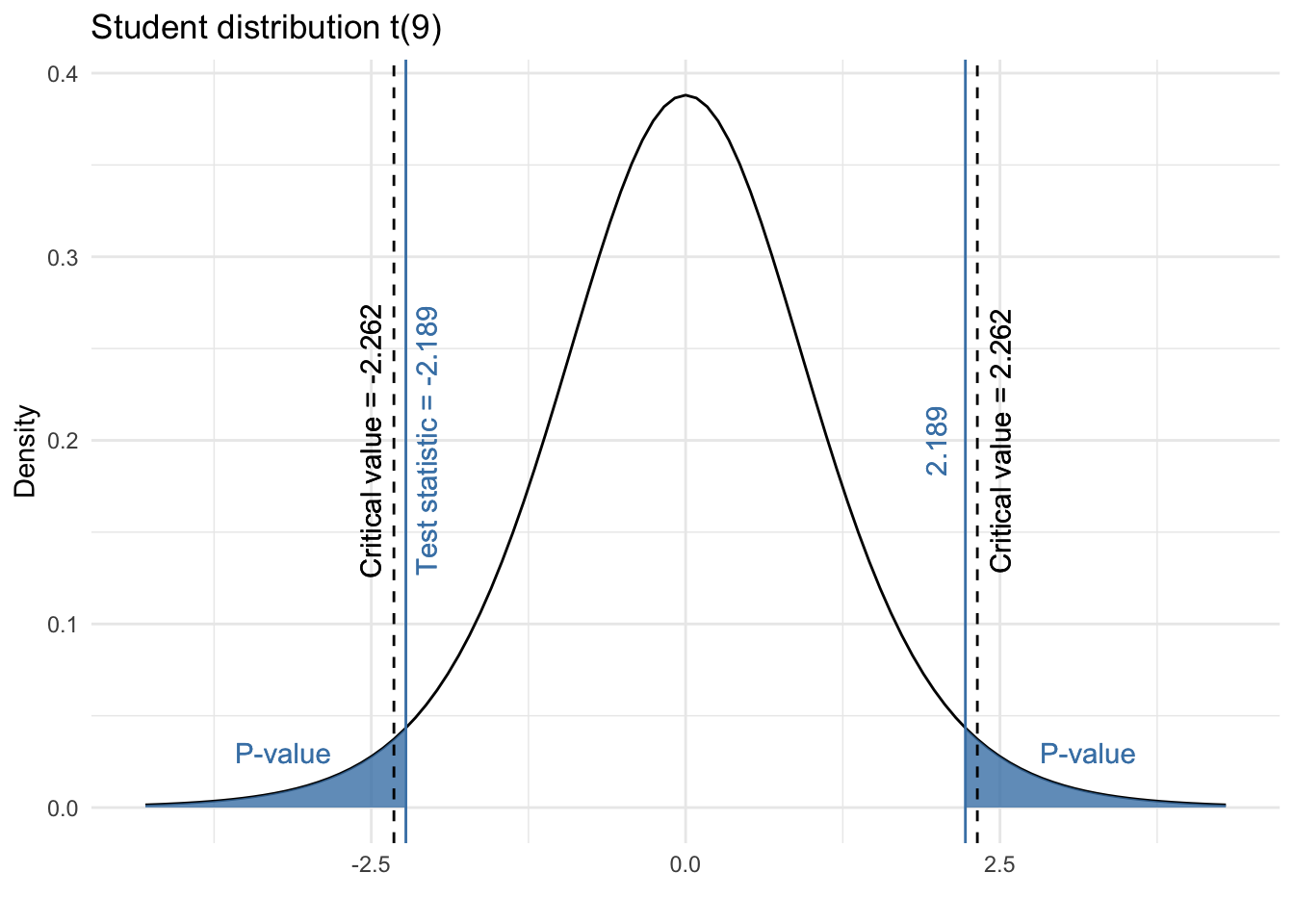
The p -value can computed with precision in R with the pt() function:
The p -value is 0.0563, which indicates that there is a 5.63% chance to observe a sample at least as extreme as the one observed if the null hypothesis were true. This already gives us a hint on whether our t-stat is too extreme or not (and thus whether our null hypothesis is likely or not), but we formally conclude in step #4.
Like the qt() function to find the critical value, we use pt() to find the p -value because the underlying distribution is the Student’s distribution.
Use pnorm() , pchisq() and pf() for the Normal, Chi-square and Fisher distribution, respectively. See also this Shiny app to compute the p -value given a certain t-stat for most probability distributions.
If you do not have access to a computer (during exams for example) you will not be able to compute the p -value precisely, but you can bound it using the statistical table referring to your test.
In our case, we use the Student distribution and we look at the row df = 9 (since df = n - 1):
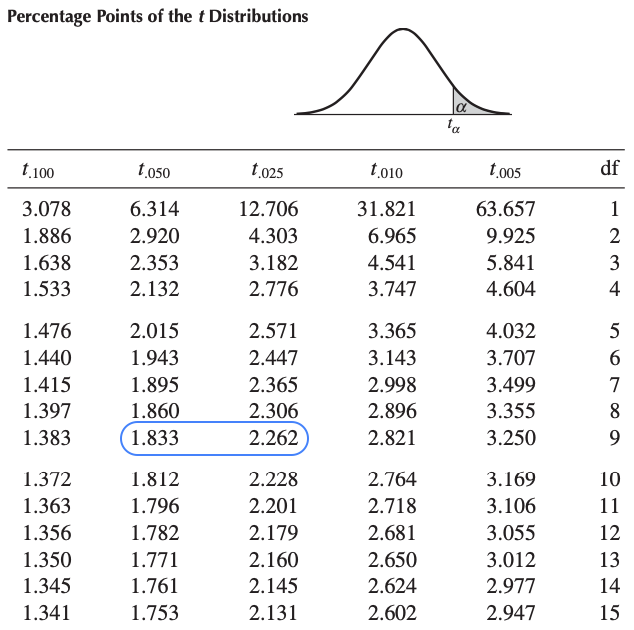
- The test statistic is -2.189
- We take the absolute value, which gives 2.189
- The value 2.189 is between 1.833 and 2.262 (highlighted in blue in the above table)
- the area to the right of 1.833 is 0.05
- the area to the right of 2.262 is 0.025
- So we know that the area to the right of 2.189 must be between 0.025 and 0.05
- Since the Student distribution is symmetric, we know that the area to the left of -2.189 must also be between 0.025 and 0.05
- Therefore, the sum of the two areas must be between 0.05 and 0.10
- In other words, the p -value is between 0.05 and 0.10 (i.e., 0.05 < p -value < 0.10)
Although we could not compute it precisely, it is enough to conclude our hypothesis test in the last step.
The final step is now to simply compare the p -value (computed in step #3) with the significance level \(\alpha\) . As for all statistical tests :
- If the p -value is smaller than \(\alpha\) ( p -value < 0.05) \(\rightarrow H_0\) is unlikely \(\rightarrow\) we reject the null hypothesis
- If the p -value is greater than or equal to \(\alpha\) ( p -value \(\ge\) 0.05) \(\rightarrow H_0\) is likely \(\rightarrow\) we do not reject the null hypothesis
No matter if we take into consideration the exact p -value (i.e., 0.0563) or the bounded one (0.05 < p -value < 0.10), it is larger than 0.05, so we do not reject the null hypothesis. 10 In the context of the problem, we do not reject the null hypothesis that the mean weight of Belgian adults is 80 kg.
Remember that rejecting (or not rejecting) a null hypothesis at the significance level \(\alpha\) using the critical value method (method A) is equivalent to rejecting (or not rejecting) the null hypothesis when the p -value is lower (equal or greater) than \(\alpha\) (method B).
This is the reason we find the exact same conclusion than with method A, and why you should too if you use both methods on the same data and with the same significance level.
Method C, which consists in computing the confidence interval and comparing this confidence interval with the target parameter (the parameter under the null hypothesis), boils down to the following 3 steps:
- Computing the confidence interval
In this last method which uses the confidence interval, the first step is similar than in the first two methods.
Like hypothesis testing, confidence intervals are a well-known tool in inferential statistics.
Confidence interval is an estimation procedure which produces an interval (i.e., a range of values) containing the true parameter with a certain —usually high— probability .
In the same way that there is a formula for each type of hypothesis test when computing the test statistics, there exists a formula for each type of confidence interval. Formulas for the different types of confidence intervals can be found in this Shiny app .
Here is the formula for a confidence interval on one mean \(\mu\) (with unknown population variance):
\[ (1-\alpha)\text{% CI for } \mu = \bar{x} \pm t_{\alpha/2, n - 1} \frac{s}{\sqrt{n}} \]
where \(t_{\alpha/2, n - 1}\) is found in the Student distribution table (and is similar to the critical value found in step #3 of method A).
Given our data and with \(\alpha\) = 0.05, we have:
\[ \begin{aligned} 95\text{% CI for } \mu &= \bar{x} \pm t_{\alpha/2, n - 1} \frac{s}{\sqrt{n}} \\ &= 71 \pm 2.262 \frac{13}{\sqrt{10}} \\ &= [61.70; 80.30] \end{aligned} \]
The 95% confidence interval for \(\mu\) is [61.70; 80.30] kg. But what does a 95% confidence interval mean?
We know that this estimation procedure has a 95% probability of producing an interval containing the true mean \(\mu\) . In other words, if we construct many confidence intervals (with different samples of the same size), 95% of them will , on average, include the mean of the population (the true parameter). So on average, 5% of these confidence intervals will not cover the true mean.
If you wish to decrease this last percentage, you can decrease the significance level (set \(\alpha\) = 0.01 or 0.02 for instance). All else being equal, this will increase the range of the confidence interval and thus increase the probability that it includes the true parameter.
The final step is simply to compare the confidence interval (constructed in step #2) with the value of the target parameter (the value under the null hypothesis, mentioned in step #1):
- If the confidence interval does not include the hypothesized value \(\rightarrow H_0\) is unlikely \(\rightarrow\) we reject the null hypothesis
- If the confidence interval includes the hypothesized value \(\rightarrow H_0\) is likely \(\rightarrow\) we do not reject the null hypothesis
In our example:
- the hypothesized value is 80 (since \(H_0: \mu\) = 80)
- 80 is included in the 95% confidence interval since it goes from 61.70 to 80.30 kg
- So we do not reject the null hypothesis
In the terms of the problem, we do not reject the hypothesis that the mean weight of Belgian adults is 80 kg.
As you can see, the conclusion is equivalent than with the critical value method (method A) and the p -value method (method B). Again, this must be the case since we use the same data and the same significance level \(\alpha\) for all three methods.
All three methods give the same conclusion. However, each method has its own advantage so I usually select the most convenient one depending on the situation:
- It is, in my opinion, the easiest and most straightforward method of the three when I do not have access to R.
- In addition to being able to know whether the null hypothesis is rejected or not, computing the exact p -value can be very convenient so I tend to use this method if I have access to R.
- If I need to test several hypothesized values , I tend to choose this method because I can construct one single confidence interval and compare it to as many values as I want. For example, with our 95% confidence interval [61.70; 80.30], I know that any value below 61.70 kg and above 80.30 kg will be rejected, without testing it for each value.
In this article, we reviewed the goals and when hypothesis testing is used. We then showed how to do a hypothesis test by hand through three different methods (A. critical value , B. p -value and C. confidence interval ). We also showed how to interpret the results in the context of the initial problem.
Although all three methods give the exact same conclusion when using the same data and the same significance level (otherwise there is a mistake somewhere), I also presented my personal preferences when it comes to choosing one method over the other two.
Thanks for reading.
I hope this article helped you to understand the structure of a hypothesis by hand. I remind you that, at least for the 6 hypothesis tests covered in this article, the formulas are different, but the structure and the reasoning behind it remain the same. So you basically have to know which formulas to use, and simply follow the steps mentioned in this article.
For the interested reader, I created two accompanying Shiny apps:
- Hypothesis testing and confidence intervals : after entering your data, the app illustrates all the steps in order to conclude the test and compute a confidence interval. See more information in this article .
- How to read statistical tables : the app helps you to compute the p -value given a t-stat for most probability distributions. See more information in this article .
As always, if you have a question or a suggestion related to the topic covered in this article, please add it as a comment so other readers can benefit from the discussion.
Suppose a researcher wants to test whether Belgian women are taller than French women. Suppose a health professional would like to know whether the proportion of smokers is different among athletes and non-athletes. It would take way too long to measure the height of all Belgian and French women and to ask all athletes and non-athletes their smoking habits. So most of the time, decisions are based on a representative sample of the population and not on the whole population. If we could measure the entire population in a reasonable time frame, we would not do any inferential statistics. ↩︎
Don’t get me wrong, this does not mean that hypothesis tests are never used in exploratory analyses. It is just much less frequent in exploratory research than in confirmatory research. ↩︎
You may see more or less steps in other articles or textbooks, depending on whether these steps are detailed or concise. Hypothesis testing should, however, follows the same process regardless of the number of steps. ↩︎
For one-sided tests, writing \(H_0: \mu = 80\) or \(H_0: \mu \ge 80\) are both correct. The point is that the null and alternative hypothesis must be mutually exclusive since you are testing one hypothesis against the other, so both cannot be true at the same time. ↩︎
To be complete, there are even different formulas within each type of test, depending on whether some assumptions are met or not. For the interested reader, see all the different scenarios and thus the different formulas for a test on one mean and on two means . ↩︎
There are more uncertainty if the population variance is unknown than if it is known, and this greater uncertainty is taken into account by using the Student distribution instead of the standard Normal distribution. Also note that as the sample size increases, the degrees of freedom of the Student distribution increases and the two distributions become more and more similar. For large sample size (usually from \(n >\) 30), the Student distribution becomes so close to the standard Normal distribution that, even if the population variance is unknown, the standard Normal distribution can be used. ↩︎
For a test on two independent samples, the degrees of freedom is \(n_1 + n_2 - 2\) , where \(n_1\) and \(n_2\) are the size of the first and second sample, respectively. Note the - 2 due to the fact that in this case, two quantities are estimated. ↩︎
The type II error is the probability of not rejecting the null hypothesis although it is in reality false. ↩︎
Whether this is a good or a bad standard is a question that comes up often and is debatable. This is, however, beyond the scope of the article. ↩︎
Again, p -values found via a statistical table or via R must be coherent. ↩︎
Related articles
- One-sample Wilcoxon test in R
- Correlation coefficient and correlation test in R
- One-proportion and chi-square goodness of fit test
- How to perform a one-sample t-test by hand and in R: test on one mean
Liked this post?
- Get updates every time a new article is published (no spam and unsubscribe anytime):
Yes, receive new posts by email
- Support the blog
FAQ Contribute Sitemap
Test for Normality in R: Three Different Methods & Interpretation
In this blog post, you will learn how to test for the normality of residuals in R. Testing the normality of residuals is a step in data analysis. It helps determine if the residuals follow a normal distribution , which is important in many fields, including data science and psychology. Approximately normal residuals allow for powerful parametric tests , while non-normal residuals can sometimes lead to inaccurate results and false conclusions.
Testing for normality in R can be done using various methods. One of the most commonly used tests is the Shapiro-Wilks test. This test tests the null hypothesis that a sample is drawn from a normal distribution. Another popular test is the Anderson-Darling test, which is more sensitive to deviations from normality in the distribution’s tails. Additionally, the Kolmogorov-Smirnov test can be used to test for normality. The Kolmogorov-Smirnov test compares the sample distribution to a normal one with the same mean and standard deviation. In addition to using various normality tests, it’s important to incorporate data visualization techniques to assess normality.
Table of Contents
Normality testing: why it’s important and how to test for normality.
Normality is a fundamental concept in statistics that refers to the distribution of a data set (residuals in our case). A normal distribution, also known as a Gaussian distribution, is a bell-shaped curve that is symmetric around the mean. In other words, the data is evenly distributed around the center of the distribution, with most values close to the mean and fewer values further away.
Examples of Normality in Data Science and Psychology
In psychology, normality is often used to describe the distribution of scores on psychological tests. For example, intelligence tests are designed to have a normal distribution, with most people scoring around the mean and fewer people scoring at the extremes. Normality is also important in hypothesis testing in psychology. Many statistical tests in psychology, such as t-tests and ANOVA, assume that the residuals are normally distributed. In some cases, violations of normality can lead to incorrect conclusions about the significance of the results.
Testing for Normality
Shapiro-wilks test.
The Shapiro-Wilks test is considered one of the most powerful normality tests. This means that it has a high ability to detect deviations from normality when they exist. However, the test is sensitive to sample size. It may detect deviations from normality in larger samples, even if the deviations are small and unlikely to affect the validity of parametric tests.
Anderson-Darling Test
Similar to the Shapiro-Wilks test, the Anderson-Darling test is based on the sample data and computes a test statistic that compares the observed distribution of the sample with the expected normal distribution. The test returns a p-value that can be compared to a significance level to determine whether the null hypothesis should be rejected.
The Kolmogorov-Smirnov Test for Normality
The Kolmogorov-Smirnov test is a statistical test used to check if a sample comes from a known distribution. Moreover, the test is non-parametric and can be used to check for normality and other distributions.
However, like other normality tests, the Kolmogorov-Smirnov test should not be used as the sole criterion for determining whether to use parametric or non-parametric tests. Instead, it should be used with factors such as the sample size, research question, and data analysis type.
Parametric Tests and Normality
Normality violated, requirements.
It would be best if you had basic statistics and data analysis knowledge to follow this blog post. Understanding normal distributions and statistical tests, such as t-tests and ANOVA, would be helpful.
Example Data
In the code chunk above, we first load the dplyr library for data manipulation.
To recode the hearing_status variable as a factor with levels “1” and “2” corresponding to “Normal” and “Hearing loss”, respectively, we use the mutate function from dplyr along with the recode_factor function. Of course, recoding the factor levels in R might not be useful, and you can skip this step.
How to Test for Normality in R: Three Methods
Shapiro-wilks test for normality, non-normal data.
In the code chunk above, an ANOVA is performed using the psych_data dataset. The ANOVA model is specified with RT as the dependent variable and Hearing as the independent variable. The results are stored in the object aov.fit .
Normal Data
Interpreting the shapiro-wilks test.
Interpreting the results from a Shapiro-Wilks test conducted in R is pretty straightforward. For the model including the reaction time variable, the p-value is less than 0.05 (for both groups), and we reject the null hypothesis that the residuals are normally distributed.
Reporting the Shapiro-Wilks Test for Normality: APA 7
The assumption of normality was assessed by using the Shapiro-Wilks test on the residuals from the ANOVA. Results indicated that the distribution of residuals deviated significantly from normal ( W = 0.56 p < 0.05; Hearing Loss: W = 0.54, p < 0.05).
According to the Shapiro-Wilk test, the residuals for the model including Working Memory Capacity as dependent variable was normally distributed ( W = 0.99, p = 0.26).
In the following section, we will examine how to carry out another normality test in R. Namely, the Anderson-Darling test.
Anderson-Darling Test for Normality
To perform the Anderson-Darling test for normality in R, we can use the ad.test() function from the nortest package in R. Here is how to perform the test on our example data:
In the code chunks above (RT and WMC), we first load the nortest library, which contains the ad.test() function for performing the Anderson-Darling test. Next, we carry out an ANOVA on the psych_data dataset, with Hearing as the independent variable and RT or wmc as the dependent variable. We save the residuals from each ANOVA object and pass them as an argument to the ad.test() function that tests the null hypothesis that the sample comes from a population with a normal distribution. This allows us to check the normality assumption for the ANOVA model’s residuals.
Interpret the Anderson-Darling Test for Normality
In the Anderson-Darling test for normality on the reaction time data for the normal-hearing group, the null hypothesis is that the residuals are normally distributed. The test result shows a statistic of A = 24.4 and a p-value smaller than 0.05. Since the p-value is smaller than the significance level of 0.05, we reject the null hypothesis. In conclusion, the residuals from the ANOVA using reaction time data as the dependent variable may not be normally distributed.
Report the Anderson-Darling Test: APA 7
The Anderson-Darling test for normality was performed on the reaction time model, and the results showed that the residuals were not normally distributed ( A =24.4 , p < .001). The same test was performed on the working memory capacity model, and the results showed that the residuals were normally distributed ( A = 0.29, p = .62).
Kolmogorov-Smirnov Test for Normality
Here are the code chunks for performing the Kolmogorov-Smirnov Test for Normality in R on the same example data:
Interpreting the Kolmogorov-Smirnov Test
How to report the kolmogorov-smirnov test: apa 7.
For the one-sample Kolmogorov-Smirnov tests, we found that the distribution of residuals was significantly different from a normal distribution ( D = 0.24, p < .001). . For the model including working memory capacity as a dependent varable, the distribution of residuals did not significantly deviate from normality ( D = 0.04, p = .89).
Again, violations of normality assumptions may only sometimes be problematic, particularly with large sample sizes or mild deviations from normality. See the previous sections on interpreting the Shapiro-Wilks and Anderson-Darling tests for more information.
Dealing with Non-normal Data
Z-score transformation, non-parametric tests.
Several non-parametric tests, such as the Wilcoxon rank-sum, Kruskal-Wallis, and Mann-Whitney U tests, can be used when data is not normally distributed. These tests do not assume normality and can be more appropriate when dealing with non-normal data. Here are some resources on this blog that may be useful:
Additional Approaches
Conclusion: test for normality in r.
By mastering the methods for testing for normality in R, you will be better equipped to conduct rigorous statistical analyses that produce accurate results and conclusions. We hope this blog post was helpful in your understanding of this crucial topic. Please share this post on social media and cite it in your work.
Leave a Comment Cancel Reply
- Stack Overflow Public questions & answers
- Stack Overflow for Teams Where developers & technologists share private knowledge with coworkers
- Talent Build your employer brand
- Advertising Reach developers & technologists worldwide
- Labs The future of collective knowledge sharing
- About the company
Collectives™ on Stack Overflow
Find centralized, trusted content and collaborate around the technologies you use most.
Q&A for work
Connect and share knowledge within a single location that is structured and easy to search.
Get early access and see previews of new features.
Seeing if data is normally distributed in R
Can someone please help me fill in the following function in R:
- normal-distribution
- 2 It's not really clear what you're asking. Are you looking for a function to evaluate whether a vector of numbers look like random draws from a normal distribution? If so, why not just say that? – Karl Oct 16, 2011 at 1:40
8 Answers 8
Normality tests don't do what most think they do. Shapiro's test, Anderson Darling, and others are null hypothesis tests AGAINST the the assumption of normality. These should not be used to determine whether to use normal theory statistical procedures. In fact they are of virtually no value to the data analyst. Under what conditions are we interested in rejecting the null hypothesis that the data are normally distributed? I have never come across a situation where a normal test is the right thing to do. When the sample size is small, even big departures from normality are not detected, and when your sample size is large, even the smallest deviation from normality will lead to a rejected null.
For example:
So, in both these cases (binomial and lognormal variates) the p-value is > 0.05 causing a failure to reject the null (that the data are normal). Does this mean we are to conclude that the data are normal? (hint: the answer is no). Failure to reject is not the same thing as accepting. This is hypothesis testing 101.
But what about larger sample sizes? Let's take the case where there the distribution is very nearly normal.

Here we are using a t-distribution with 200 degrees of freedom. The qq-plot shows the distribution is closer to normal than any distribution you are likely to see in the real world, but the test rejects normality with a very high degree of confidence.
Does the significant test against normality mean that we should not use normal theory statistics in this case? (another hint: the answer is no :) )
- 10 Very nice. The big follow-up question (which I have yet to find a satisfactory answer for, and would love to have a simple answer to give my students, but I doubt there is one) is: if one is using graphical diagnostics of a regression, how ( other than fitting a model/following a procedure that is robust against a certain class of violation [e.g. robust models, generalized least squares,] and showing that its results do not differ interestingly) does one decide whether to worry about a particular type of violation? – Ben Bolker Oct 17, 2011 at 1:59
- 19 For linear regression... 1. Don't worry much about normality. The CLT takes over quickly and if you have all but the smallest sample sizes and an even remotely reasonable looking histogram you are fine. 2. Worry about unequal variances (heteroskedasticity). I worry about this to the point of (almost) using HCCM tests by default. A scale location plot will give some idea of whether this is broken, but not always. Also, there is no a priori reason to assume equal variances in most cases. 3. Outliers. A cooks distance of > 1 is reasonable cause for concern. Those are my thoughts (FWIW). – Ian Fellows Oct 17, 2011 at 5:02
- 3 @IanFellows: you sure wrote a lot, but you didn't answer the OP's question. Is there a single function that returns TRUE or FALSE for whether data is normal or not? – stackoverflowuser2010 Nov 23, 2014 at 21:42
- 5 @stackoverflowuser2010, Here are two definitive answers to your simple question: (1) You can never, no matter how much data you collect, conclusively determine that it was generated from an exactly normal distribution. (2) Your data is not generated from an exactly normal distribution (no real data is). – Ian Fellows Nov 24, 2014 at 18:50
- 15 @stackoverflowuser2010, that is adorable. I particularly like the personal shot. You may have wanted to try googling me before you took it though. – Ian Fellows Nov 24, 2014 at 19:53
I would also highly recommend the SnowsPenultimateNormalityTest in the TeachingDemos package. The documentation of the function is far more useful to you than the test itself, though. Read it thoroughly before using the test.
- SnowsPenultimateNormalityTest reminds me of thix XKCD comic :) – adilapapaya Nov 11, 2017 at 20:11
SnowsPenultimateNormalityTest certainly has its virtues, but you may also want to look at qqnorm .
Consider using the function shapiro.test , which performs the Shapiro-Wilks test for normality. I've been happy with it.
- 4 This is generally reserved for small samples (n < 50), but can be used with samples up to ~ 2000 - Which I would consider a relatively small sample size. – derelict Feb 17, 2014 at 22:26
- 4 I don't want to be too negative, but (ignoring all of the larger-context answers here about why normality testing might be a bad idea), I'm worried about this package -- the tests it uses are undocumented. How does it differ from the tests in base R and in the nortest and normtest packages (Shapiro-Wilk, Anderson-Darling, Jarque-Bera, ...), all of which are very carefully characterized in the statistical literature? – Ben Bolker Nov 16, 2014 at 12:56
- having spent a few more seconds looking at the package, I think I can say it's pretty crude. It divides the data into bins and does a chi-squared test; while general, this approach is almost certainly less powerful than the better-known tests. – Ben Bolker Mar 14, 2018 at 1:23
The Anderson-Darling test is also be useful.
- If p-value is less than 0.05, does it mean that data is normally distributed? – ah bon May 7, 2020 at 9:28
In addition to qqplots and the Shapiro-Wilk test, the following methods may be useful.
Qualitative:
- histogram compared to the normal
- cdf compared to the normal
- ggdensity plot
Quantitative:
- nortest package normality tests
- normtest package normality tests
The qualitive methods can be produced using the following in R:
A word of caution - don't blindly apply tests. Having a solid understanding of stats will help you understand when to use which tests and the importance of assumptions in hypothesis testing.
when you perform a test, you ever have the probabilty to reject the null hypothesis when it is true.
See the nextt R code:
The graph shows that whether you have a sample size small or big a 5% of the times you have a chance to reject the null hypothesis when it s true (a Type-I error)
Not the answer you're looking for? Browse other questions tagged r normal-distribution or ask your own question .
- Featured on Meta
- The 2024 Developer Survey Is Live
- The return of Staging Ground to Stack Overflow
- The [tax] tag is being burninated
- Policy: Generative AI (e.g., ChatGPT) is banned
Hot Network Questions
- Movie I saw in the 80s where a substance oozed off of movie stairs leaving a wet cat behind
- Can we combine a laser with a gauss rifle to get a cinematic 'laser rifle'?
- Do reflective warning triangles blow away in wind storms?
- 1h 10m international > domestic transit at IST (Istanbul) on a single ticket
- My players think they found a loophole that gives them infinite poison and XP. How can I add the proper challenges to slow them down?
- Create repeating geometry across a face
- Is the B-theory of time only compatible with an infinitely renewing cyclical reality?
- Starlink Satellite Orbits
- British child with Italian mother. Which document can she use to travel to/from Italy on her own?
- Do you still cross out and redo the page numbers if you do it wrong in your scientific notebook?
- Expected Amp difference going from SEU-AL to Copper on HVAC?
- Cryptic Clue Explanation: Tree that's sported to keep visitors out at university (3)
- How do Authenticators work?
- What's the difference between cryogenic and Liquid propellant?
- Commutativity of the wreath product
- Executable files with a bytecode compiler/interpreter
- Group with a translation invariant ultrafilter
- Have I ruined my AC by running it with the outside cover on?
- For the square wave signal, why does a narrower square wave correspond to more spread in the frequency domain?
- Is there a phrase like "etymologically related" but for food?
- How big can a chicken get?
- Ubuntu Terminal with alternating colours for each line
- Selecting an opamp for a voltage follower circuit using a LTspice simulation
- Was it known in ancient Rome and Greece that boiling water made it safe to drink and if so, what was the theory behind this?
7.4.1 - Hypothesis Testing
Five step hypothesis testing procedure.
In the remaining lessons, we will use the following five step hypothesis testing procedure. This is slightly different from the five step procedure that we used when conducting randomization tests.
- Check assumptions and write hypotheses. The assumptions will vary depending on the test. In this lesson we'll be confirming that the sampling distribution is approximately normal by visually examining the randomization distribution. In later lessons you'll learn more objective assumptions. The null and alternative hypotheses will always be written in terms of population parameters; the null hypothesis will always contain the equality (i.e., \(=\)).
- Calculate the test statistic. Here, we'll be using the formula below for the general form of the test statistic.
- Determine the p-value. The p-value is the area under the standard normal distribution that is more extreme than the test statistic in the direction of the alternative hypothesis.
- Make a decision. If \(p \leq \alpha\) reject the null hypothesis. If \(p>\alpha\) fail to reject the null hypothesis.
- State a "real world" conclusion. Based on your decision in step 4, write a conclusion in terms of the original research question.
General Form of a Test Statistic
When using a standard normal distribution (i.e., z distribution), the test statistic is the standardized value that is the boundary of the p-value. Recall the formula for a z score: \(z=\frac{x-\overline x}{s}\). The formula for a test statistic will be similar. When conducting a hypothesis test the sampling distribution will be centered on the null parameter and the standard deviation is known as the standard error.
This formula puts our observed sample statistic on a standard scale (e.g., z distribution). A z score tells us where a score lies on a normal distribution in standard deviation units. The test statistic tells us where our sample statistic falls on the sampling distribution in standard error units.
7.4.1.1 - Video Example: Mean Body Temperature
Research question: Is the mean body temperature in the population different from 98.6° Fahrenheit?
7.4.1.2 - Video Example: Correlation Between Printer Price and PPM
Research question: Is there a positive correlation in the population between the price of an ink jet printer and how many pages per minute (ppm) it prints?
7.4.1.3 - Example: Proportion NFL Coin Toss Wins
Research question: Is the proportion of NFL overtime coin tosses that are won different from 0.50?
StatKey was used to construct a randomization distribution:
Step 1: Check assumptions and write hypotheses
From the given StatKey output, the randomization distribution is approximately normal.
\(H_0\colon p=0.50\)
\(H_a\colon p \ne 0.50\)
Step 2: Calculate the test statistic
\(test\;statistic=\dfrac{sample\;statistic-null\;parameter}{standard\;error}\)
The sample statistic is the proportion in the original sample, 0.561. The null parameter is 0.50. And, the standard error is 0.024.
\(test\;statistic=\dfrac{0.561-0.50}{0.024}=\dfrac{0.061}{0.024}=2.542\)
Step 3: Determine the p value
The p value will be the area on the z distribution that is more extreme than the test statistic of 2.542, in the direction of the alternative hypothesis. This is a two-tailed test:
The p value is the area in the left and right tails combined: \(p=0.0055110+0.0055110=0.011022\)
Step 4: Make a decision
The p value (0.011022) is less than the standard 0.05 alpha level, therefore we reject the null hypothesis.
Step 5: State a "real world" conclusion
There is evidence that the proportion of all NFL overtime coin tosses that are won is different from 0.50
7.4.1.4 - Example: Proportion of Women Students
Research question : Are more than 50% of all World Campus STAT 200 students women?
Data were collected from a representative sample of 501 World Campus STAT 200 students. In that sample, 284 students were women and 217 were not women.
StatKey was used to construct a sampling distribution using randomization methods:
Because this randomization distribution is approximately normal, we can find the p value by computing a standardized test statistic and using the z distribution.
The assumption here is that the sampling distribution is approximately normal. From the given StatKey output, the randomization distribution is approximately normal.
\(H_0\colon p=0.50\) \(H_a\colon p>0.50\)
2. Calculate the test statistic
\(test\;statistic=\dfrac{sample\;statistic-hypothesized\;parameter}{standard\;error}\)
The sample statistic is \(\widehat p = 284/501 = 0.567\).
The hypothesized parameter is the value from the hypotheses: \(p_0=0.50\).
The standard error on the randomization distribution above is 0.022.
\(test\;statistic=\dfrac{0.567-0.50}{0.022}=3.045\)
3. Determine the p value
We can find the p value by constructing a standard normal distribution and finding the area under the curve that is more extreme than our observed test statistic of 3.045, in the direction of the alternative hypothesis. In other words, \(P(z>3.045)\):
Our p value is 0.0011634
4. Make a decision
Our p value is less than or equal to the standard 0.05 alpha level, therefore we reject the null hypothesis.
5. State a "real world" conclusion
There is evidence that the proportion of all World Campus STAT 200 students who are women is greater than 0.50.
7.4.1.5 - Example: Mean Quiz Score
Research question: Is the mean quiz score different from 14 in the population?
\(H_0\colon \mu = 14\)
\(H_a\colon \mu \ne 14\)
The sample statistic is the mean in the original sample, 13.746 points. The null parameter is 14 points. And, the standard error, 0.142, can be found on the StatKey output.
\(test\;statistic=\dfrac{13.746-14}{0.142}=\dfrac{-0.254}{0.142}=-1.789\)
The p value will be the area on the z distribution that is more extreme than the test statistic of -1.789, in the direction of the alternative hypothesis:
This was a two-tailed test. The p value is the area in the left and right tails combined: \(p=0.0368074+0.0368074=0.0736148\)
The p value (0.0736148) is greater than the standard 0.05 alpha level, therefore we fail to reject the null hypothesis.
There is not enough evidence to state that the mean quiz score in the population is different from 14 points.
7.4.1.6 - Example: Difference in Mean Commute Times
Research question: Do the mean commute times in Atlanta and St. Louis differ in the population?
From the given StatKey output, the randomization distribution is approximately normal.
\(H_0: \mu_1-\mu_2=0\)
\(H_a: \mu_1 - \mu_2 \ne 0\)
Step 2: Compute the test statistic
\(test\;statistic=\dfrac{sample\;statistic - null \; parameter}{standard \;error}\)
The observed sample statistic is \(\overline x _1 - \overline x _2 = 7.14\). The null parameter is 0. And, the standard error, from the StatKey output, is 1.136.
\(test\;statistic=\dfrac{7.14-0}{1.136}=6.285\)
The p value will be the area on the z distribution that is more extreme than the test statistic of 6.285, in the direction of the alternative hypothesis:
This was a two-tailed test. The area in the two tailed combined is 0.000000. Theoretically, the p value cannot be 0 because there is always some chance that a Type I error was committed. This p value would be written as p < 0.001.
The p value is smaller than the standard 0.05 alpha level, therefore we reject the null hypothesis.
There is evidence that the mean commute times in Atlanta and St. Louis are different in the population.
- Introduction to Machine Learning
- Machine Learning with R
- Machine Learning with Python
- Statistics in R
- Math for Machine Learning
- Machine Learning Interview Questions
- Projects in R
- Deep Learning with R
- AI Algorithm
- How to Normalize Data in R?
- How to Perform a Wald Test in R
- How to Perform Runs Test in R
- How to Perform McNemar’s Test in R
- How to Perform an F-Test in Python
- How to Normalize and Standardize Data in R?
- How to Perform Dunn’s Test in Python
- How to Perform Grubbs’ Test in Python
- How to Perform Multivariate Normality Tests in Python
- How to Perform Bartlett’s Test in Python?
- How to Normalize Data in Excel?
- How to Create Summary Tables in R?
- How to Perform Fisher’s Exact Test in Python
- How to perform T-tests in MS Excel?
- How to Conduct a Sobel Test in R
- How to Calculate Normality of a Solution?
- How to Perform a Shapiro-Wilk Test in Python
- How to Use the replicate() Function in R?
- How to Create a Residual Plot in R
How to Test for Normality in R
Normality testing is important in statistics since it ensures the validity of various analytical procedures. Understanding whether data follows a normal distribution is critical for drawing appropriate conclusions and predictions. In this article, we look at the methods and approaches for assessing normalcy in the R Programming Language .
What is Normality Testing?
Normality testing determines if a particular dataset has a normal distribution. A normal distribution, sometimes called a Gaussian distribution, is distinguished by a symmetric bell-shaped curve. This assessment is critical since many statistical procedures, including t-tests , ANOVA, and linear regression, are based on the assumption of normality.
How to Perform Normality Testing in R
To do normality testing in R, first, install and load the required packages. Then, import your dataset into the R environment and perform the necessary normality test. Typically, while interpreting the data, the test statistic and related p-value are assessed.
Types of Normality Tests in R
In R, several methods are available for testing normality including :
- Shapiro-Wilk test
- Kolmogorov-Smirnov test
- Anderson-Darling test
Each test includes unique assumptions and statistical features, making it appropriate for a variety of contexts.
1. Shapiro-Wilk Test
The Shapiro-Wilk test is a statistical test that determines if a dataset represents a regularly distributed population.
2. Kolmogorov-Smirnov Test
The Kolmogorov-Smirnov test is a non-parametric test that determines if a dataset has a certain distribution.
3. Anderson-Darling Test
The Anderson-Darling test is a statistical test that determines if a dataset follows a specific distribution, notably the normal distribution.
Implications of Different P-Values
The significance of the p-value derived from normalcy testing cannot be overstated. A p-value that is less than a selected significance threshold (usually 0.05) indicates evidence that the null hypothesis of normality is not true. A larger p-value, on the other hand, suggests that there is insufficient data to rule out the null hypothesis. Comprehending these ramifications facilitates an efficient interpretation of the findings.
Graphical Methods for Testing Normality
Q-q plots (quantile-quantile plots), box plots and density plots.
Q-Q plots are a type of graphical tool that are used to determine if a dataset is distributed normally or not. Q-Q plots may be made in R with the qqnorm() and qqline() functions. Q-Q plots reveal various patterns that might shed light on the deviation from normalcy.

Normality in R
Histograms offer a graphic depiction of the data distribution. Histograms may be made in R by utilising the hist() function. An analysis of the histogram’s form might reveal departures from the norm.

For examining the data distribution graphically, box plots and density plots are helpful. Density plots depict the distribution of the data as a smooth curve, whereas box plots highlight the dispersion and central tendency of the distribution. When evaluating data distribution, these graphs can be used in addition to traditional normalcy tests.

In conclusion, checking for normalcy is an important stage in statistical analysis since it ensures the validity of subsequent inference and decision-making. Using a mix of numerical tests.

Please Login to comment...
Similar reads.
- R Machine Learning
Improve your Coding Skills with Practice
What kind of Experience do you want to share?
P-Value And Statistical Significance: What It Is & Why It Matters
Saul Mcleod, PhD
Editor-in-Chief for Simply Psychology
BSc (Hons) Psychology, MRes, PhD, University of Manchester
Saul Mcleod, PhD., is a qualified psychology teacher with over 18 years of experience in further and higher education. He has been published in peer-reviewed journals, including the Journal of Clinical Psychology.
Learn about our Editorial Process
Olivia Guy-Evans, MSc
Associate Editor for Simply Psychology
BSc (Hons) Psychology, MSc Psychology of Education
Olivia Guy-Evans is a writer and associate editor for Simply Psychology. She has previously worked in healthcare and educational sectors.
On This Page:
The p-value in statistics quantifies the evidence against a null hypothesis. A low p-value suggests data is inconsistent with the null, potentially favoring an alternative hypothesis. Common significance thresholds are 0.05 or 0.01.
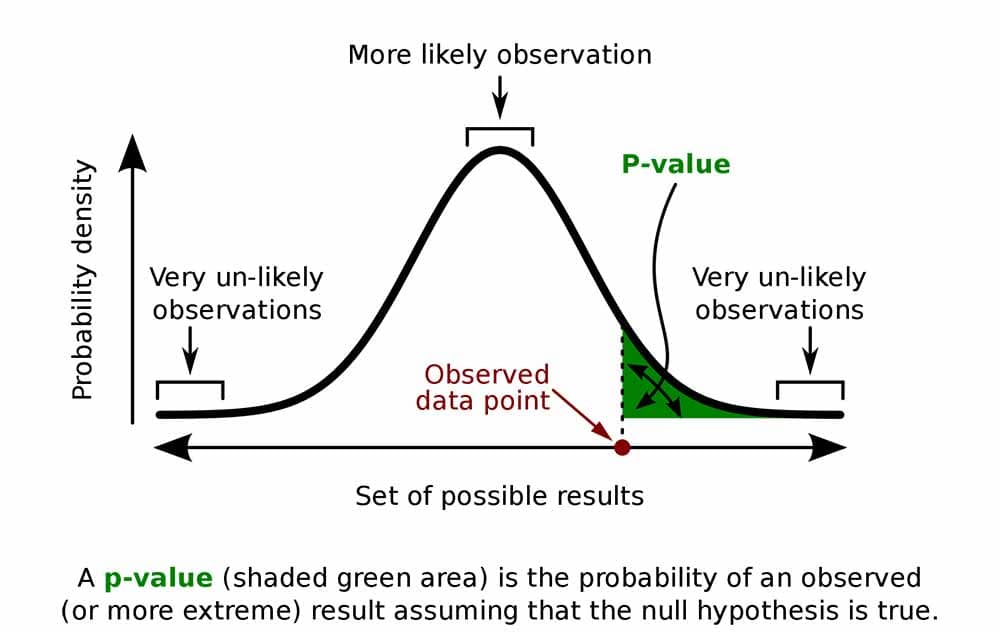
Hypothesis testing
When you perform a statistical test, a p-value helps you determine the significance of your results in relation to the null hypothesis.
The null hypothesis (H0) states no relationship exists between the two variables being studied (one variable does not affect the other). It states the results are due to chance and are not significant in supporting the idea being investigated. Thus, the null hypothesis assumes that whatever you try to prove did not happen.
The alternative hypothesis (Ha or H1) is the one you would believe if the null hypothesis is concluded to be untrue.
The alternative hypothesis states that the independent variable affected the dependent variable, and the results are significant in supporting the theory being investigated (i.e., the results are not due to random chance).
What a p-value tells you
A p-value, or probability value, is a number describing how likely it is that your data would have occurred by random chance (i.e., that the null hypothesis is true).
The level of statistical significance is often expressed as a p-value between 0 and 1.
The smaller the p -value, the less likely the results occurred by random chance, and the stronger the evidence that you should reject the null hypothesis.
Remember, a p-value doesn’t tell you if the null hypothesis is true or false. It just tells you how likely you’d see the data you observed (or more extreme data) if the null hypothesis was true. It’s a piece of evidence, not a definitive proof.
Example: Test Statistic and p-Value
Suppose you’re conducting a study to determine whether a new drug has an effect on pain relief compared to a placebo. If the new drug has no impact, your test statistic will be close to the one predicted by the null hypothesis (no difference between the drug and placebo groups), and the resulting p-value will be close to 1. It may not be precisely 1 because real-world variations may exist. Conversely, if the new drug indeed reduces pain significantly, your test statistic will diverge further from what’s expected under the null hypothesis, and the p-value will decrease. The p-value will never reach zero because there’s always a slim possibility, though highly improbable, that the observed results occurred by random chance.
P-value interpretation
The significance level (alpha) is a set probability threshold (often 0.05), while the p-value is the probability you calculate based on your study or analysis.
A p-value less than or equal to your significance level (typically ≤ 0.05) is statistically significant.
A p-value less than or equal to a predetermined significance level (often 0.05 or 0.01) indicates a statistically significant result, meaning the observed data provide strong evidence against the null hypothesis.
This suggests the effect under study likely represents a real relationship rather than just random chance.
For instance, if you set α = 0.05, you would reject the null hypothesis if your p -value ≤ 0.05.
It indicates strong evidence against the null hypothesis, as there is less than a 5% probability the null is correct (and the results are random).
Therefore, we reject the null hypothesis and accept the alternative hypothesis.
Example: Statistical Significance
Upon analyzing the pain relief effects of the new drug compared to the placebo, the computed p-value is less than 0.01, which falls well below the predetermined alpha value of 0.05. Consequently, you conclude that there is a statistically significant difference in pain relief between the new drug and the placebo.
What does a p-value of 0.001 mean?
A p-value of 0.001 is highly statistically significant beyond the commonly used 0.05 threshold. It indicates strong evidence of a real effect or difference, rather than just random variation.
Specifically, a p-value of 0.001 means there is only a 0.1% chance of obtaining a result at least as extreme as the one observed, assuming the null hypothesis is correct.
Such a small p-value provides strong evidence against the null hypothesis, leading to rejecting the null in favor of the alternative hypothesis.
A p-value more than the significance level (typically p > 0.05) is not statistically significant and indicates strong evidence for the null hypothesis.
This means we retain the null hypothesis and reject the alternative hypothesis. You should note that you cannot accept the null hypothesis; we can only reject it or fail to reject it.
Note : when the p-value is above your threshold of significance, it does not mean that there is a 95% probability that the alternative hypothesis is true.
One-Tailed Test
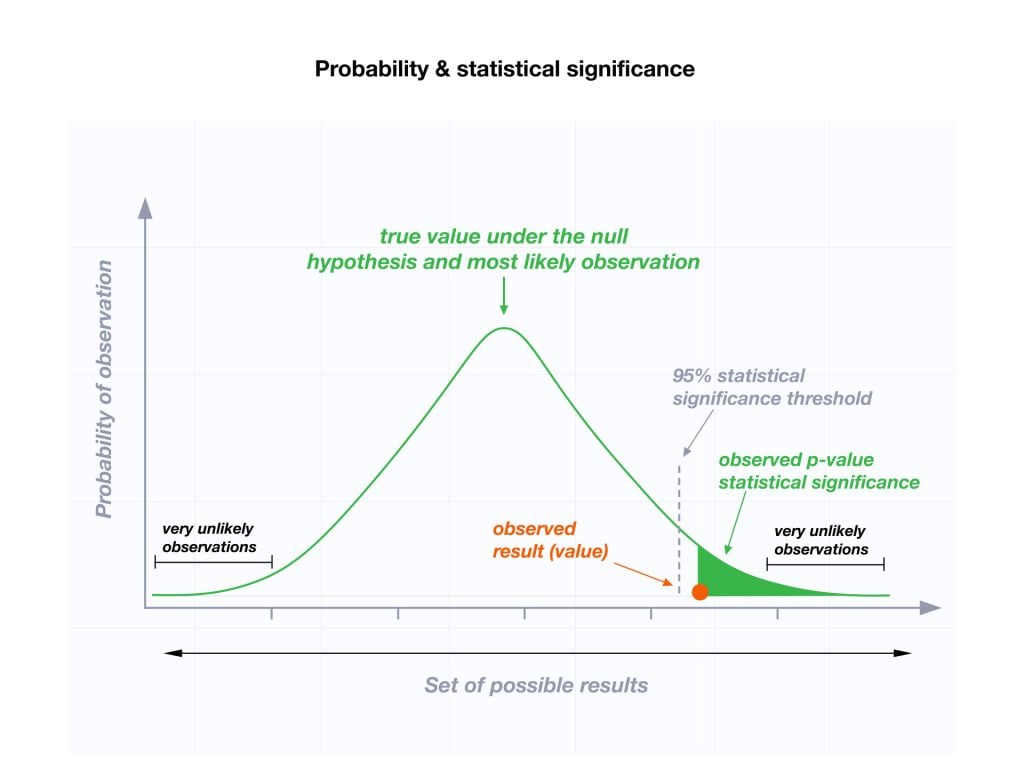
Two-Tailed Test
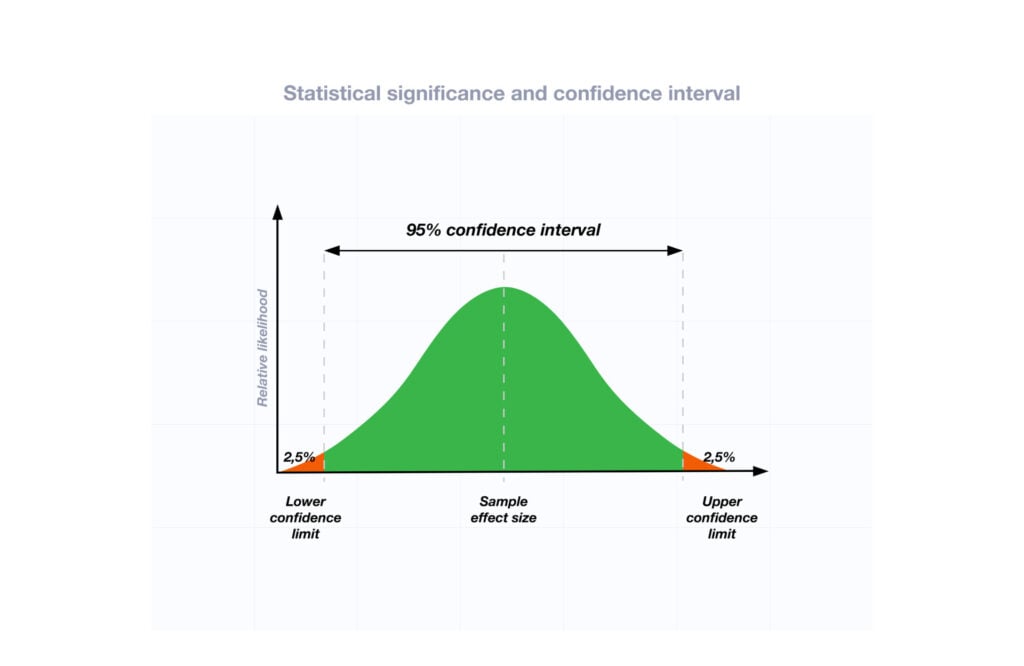
How do you calculate the p-value ?
Most statistical software packages like R, SPSS, and others automatically calculate your p-value. This is the easiest and most common way.
Online resources and tables are available to estimate the p-value based on your test statistic and degrees of freedom.
These tables help you understand how often you would expect to see your test statistic under the null hypothesis.
Understanding the Statistical Test:
Different statistical tests are designed to answer specific research questions or hypotheses. Each test has its own underlying assumptions and characteristics.
For example, you might use a t-test to compare means, a chi-squared test for categorical data, or a correlation test to measure the strength of a relationship between variables.
Be aware that the number of independent variables you include in your analysis can influence the magnitude of the test statistic needed to produce the same p-value.
This factor is particularly important to consider when comparing results across different analyses.
Example: Choosing a Statistical Test
If you’re comparing the effectiveness of just two different drugs in pain relief, a two-sample t-test is a suitable choice for comparing these two groups. However, when you’re examining the impact of three or more drugs, it’s more appropriate to employ an Analysis of Variance ( ANOVA) . Utilizing multiple pairwise comparisons in such cases can lead to artificially low p-values and an overestimation of the significance of differences between the drug groups.
How to report
A statistically significant result cannot prove that a research hypothesis is correct (which implies 100% certainty).
Instead, we may state our results “provide support for” or “give evidence for” our research hypothesis (as there is still a slight probability that the results occurred by chance and the null hypothesis was correct – e.g., less than 5%).
Example: Reporting the results
In our comparison of the pain relief effects of the new drug and the placebo, we observed that participants in the drug group experienced a significant reduction in pain ( M = 3.5; SD = 0.8) compared to those in the placebo group ( M = 5.2; SD = 0.7), resulting in an average difference of 1.7 points on the pain scale (t(98) = -9.36; p < 0.001).
The 6th edition of the APA style manual (American Psychological Association, 2010) states the following on the topic of reporting p-values:
“When reporting p values, report exact p values (e.g., p = .031) to two or three decimal places. However, report p values less than .001 as p < .001.
The tradition of reporting p values in the form p < .10, p < .05, p < .01, and so forth, was appropriate in a time when only limited tables of critical values were available.” (p. 114)
- Do not use 0 before the decimal point for the statistical value p as it cannot equal 1. In other words, write p = .001 instead of p = 0.001.
- Please pay attention to issues of italics ( p is always italicized) and spacing (either side of the = sign).
- p = .000 (as outputted by some statistical packages such as SPSS) is impossible and should be written as p < .001.
- The opposite of significant is “nonsignificant,” not “insignificant.”
Why is the p -value not enough?
A lower p-value is sometimes interpreted as meaning there is a stronger relationship between two variables.
However, statistical significance means that it is unlikely that the null hypothesis is true (less than 5%).
To understand the strength of the difference between the two groups (control vs. experimental) a researcher needs to calculate the effect size .
When do you reject the null hypothesis?
In statistical hypothesis testing, you reject the null hypothesis when the p-value is less than or equal to the significance level (α) you set before conducting your test. The significance level is the probability of rejecting the null hypothesis when it is true. Commonly used significance levels are 0.01, 0.05, and 0.10.
Remember, rejecting the null hypothesis doesn’t prove the alternative hypothesis; it just suggests that the alternative hypothesis may be plausible given the observed data.
The p -value is conditional upon the null hypothesis being true but is unrelated to the truth or falsity of the alternative hypothesis.
What does p-value of 0.05 mean?
If your p-value is less than or equal to 0.05 (the significance level), you would conclude that your result is statistically significant. This means the evidence is strong enough to reject the null hypothesis in favor of the alternative hypothesis.
Are all p-values below 0.05 considered statistically significant?
No, not all p-values below 0.05 are considered statistically significant. The threshold of 0.05 is commonly used, but it’s just a convention. Statistical significance depends on factors like the study design, sample size, and the magnitude of the observed effect.
A p-value below 0.05 means there is evidence against the null hypothesis, suggesting a real effect. However, it’s essential to consider the context and other factors when interpreting results.
Researchers also look at effect size and confidence intervals to determine the practical significance and reliability of findings.
How does sample size affect the interpretation of p-values?
Sample size can impact the interpretation of p-values. A larger sample size provides more reliable and precise estimates of the population, leading to narrower confidence intervals.
With a larger sample, even small differences between groups or effects can become statistically significant, yielding lower p-values. In contrast, smaller sample sizes may not have enough statistical power to detect smaller effects, resulting in higher p-values.
Therefore, a larger sample size increases the chances of finding statistically significant results when there is a genuine effect, making the findings more trustworthy and robust.
Can a non-significant p-value indicate that there is no effect or difference in the data?
No, a non-significant p-value does not necessarily indicate that there is no effect or difference in the data. It means that the observed data do not provide strong enough evidence to reject the null hypothesis.
There could still be a real effect or difference, but it might be smaller or more variable than the study was able to detect.
Other factors like sample size, study design, and measurement precision can influence the p-value. It’s important to consider the entire body of evidence and not rely solely on p-values when interpreting research findings.
Can P values be exactly zero?
While a p-value can be extremely small, it cannot technically be absolute zero. When a p-value is reported as p = 0.000, the actual p-value is too small for the software to display. This is often interpreted as strong evidence against the null hypothesis. For p values less than 0.001, report as p < .001
Further Information
- P-values and significance tests (Kahn Academy)
- Hypothesis testing and p-values (Kahn Academy)
- Wasserstein, R. L., Schirm, A. L., & Lazar, N. A. (2019). Moving to a world beyond “ p “< 0.05”.
- Criticism of using the “ p “< 0.05”.
- Publication manual of the American Psychological Association
- Statistics for Psychology Book Download
Bland, J. M., & Altman, D. G. (1994). One and two sided tests of significance: Authors’ reply. BMJ: British Medical Journal , 309 (6958), 874.
Goodman, S. N., & Royall, R. (1988). Evidence and scientific research. American Journal of Public Health , 78 (12), 1568-1574.
Goodman, S. (2008, July). A dirty dozen: twelve p-value misconceptions . In Seminars in hematology (Vol. 45, No. 3, pp. 135-140). WB Saunders.
Lang, J. M., Rothman, K. J., & Cann, C. I. (1998). That confounded P-value. Epidemiology (Cambridge, Mass.) , 9 (1), 7-8.
Related Articles

Exploratory Data Analysis

Research Methodology , Statistics
What Is Face Validity In Research? Importance & How To Measure

Criterion Validity: Definition & Examples
Convergent Validity: Definition and Examples

Content Validity in Research: Definition & Examples

Construct Validity In Psychology Research
- Study Guides
- Homework Questions
Testing Normal Distribution & Independence in Clinical Trials
- Skip to secondary menu
- Skip to main content
- Skip to primary sidebar
Statistics By Jim
Making statistics intuitive
Cumulative Distribution Function (CDF): Uses, Graphs & vs PDF
By Jim Frost 2 Comments
What is a Cumulative Distribution Function?
A cumulative distribution function (CDF) describes the probabilities of a random variable having values less than or equal to x. It is a cumulative function because it sums the total likelihood up to that point. Its output always ranges between 0 and 1.
CDFs have the following definition:
CDF(x) = P(X ≤ x)
Where X is the random variable, and x is a specific value. The CDF gives us the probability that the random variable X is less than or equal to x. These functions are non-decreasing. As x increases, the likelihood can either increase or stay constant, but it can’t decrease.
Both probability density functions (PDFs) and cumulative distribution functions provide likelihoods for random variables. However, PDFs calculate probability densities for x, while CDFs give the chances for ≤ x. Learn about Probability Density Functions .
Cumulative distribution functions exist for both continuous and discrete variables. Continuous functions find solutions using integrals, while discrete functions sum the probabilities for all discrete values that are less than or equal to each value. Statisticians refer to discrete functions as Probability Mass Functions .
Read on to learn why you’d use a cumulative distribution function, graph them, and learn more about how a CDF vs PDF differs.
Learn more about Cumulative Frequencies: Finding & Interpreting .
Using Cumulative Distribution Functions
Cumulative distribution functions are excellent for providing probabilities that the next observation will be less than or equal to the value you specify. This ability can help you make decisions that incorporate uncertainty.
Additionally, these cumulative probabilities are equivalent to percentiles. A cumulative probability of 0.80 is the same as the 80 th percentile. So, CDFs are great for finding percentiles. Learn more about Percentiles: Interpretations and Calculations .
For example, consider the height of an adult male in the United States. We can use the cumulative distribution function to find the probability that a person is less than or equal to 6 feet tall.
For CDF’s, we need to specify the type of distribution (e.g., normal, Weibull, binomial, etc.) and its parameters —just like we do for PDFs.
Adult males in the U.S. have heights that follow a normal distribution with a mean of 69.2 inches and a standard deviation of 2.66 inches. Consequently, we’ll need to use a normal CDF with these parameters to answer our question. Because we’re working in inches, I’ll enter 72 inches for 6 feet.
The typical CDF statistical output from your software or online calculator will look like the following:

The probability that an adult male will be 6 feet tall or shorter is 0.853745. Equivalently, you can say that a 6’ tall adult male is at the 85.4 th percentile.
Related post : Normal Distribution
Comparing Distributions
Cumulative distribution functions are fantastic for comparing two distributions. By comparing the CDFs of two random variables, we can see if one is more likely to be less than or equal to a specific value than the other. That helps us make decisions about whether one is more likely to have a particular property.
Imagine we’re a clothing manufacturer and want to compare the prevalence of 6’ tall men to women.
Next, we’ll use the normal CDF to find the probability that an adult woman will be 6’ tall or less. Women’s heights follow a normal distribution with a mean of 64.3 inches and a standard deviation of 2.58 inches.

The statistical output for the normal CDF indicates that women have a probability of 0.99858 for being ≤ 6’. That’s equivalent to the 99.9 th percentile.
85.4% of men and 99.9% of women are shorter than 6’. By dividing the inverse probabilities (1 – p), we find that men more than 6 feet tall are 103 times more likely to occur than women. As a clothing manufacturer, knowing that is helpful. A woman more than 6 feet tall is a rarity!
Graphing Normal CDFs
I always think graphs bring statistical concepts to life. So, let’s graph a cumulative distribution function to see it. We’ll return to the normal CDF for men’s heights.
On a cumulative distribution function plot, the horizontal axis displays the x values, while the vertical axis displays cumulative probabilities or percentiles. The curve represents corresponding pairs of x values and cumulative probabilities. For normal CDFs, the function sums from negative infinity up to the value of x, which is (-∞, x] in interval notation. Continuous variables produce a smooth curve, like below, while discrete variables produce a stepped function.

On the CDF graph for men’s heights, I’ve added a reference line at 6’ (i.e., 72”) to show the corresponding probability of 0.854, matching the earlier answer with rounding. Using these graphs, you can easily find probabilities and percentiles for other values. For instance, 70 inches (5′ 10″) is around the 60th percentile.
For comparison, the women’s chart is below. While the graph ends at 72 inches, the distribution actually extends to infinity in both directions.

A height of 6 feet is in the tail of the distribution.
Cumulative distribution functions (CDF) and probability distribution functions (PDF) both describe a random variable’s distribution. Both types of functions display the same underlying probability information but in a different manner. In simple terms, the PDF displays the shape of the distribution, while the CDF depicts the accumulation of probabilities as the value of the random variable increases. Learn more about Probability Distribution: Definition & Calculations .
PDFs can find cumulative probabilities by calculating the likelihood for a range up to a particular value. The PDF below shows the probability for the shaded area representing male heights up to 6’ (72”).

It finds the same probability as the CDF, showing how they present the same underlying information in a different format.
Now, imagine that you started with the shaded area to the left side of the PDF and systematically move it to the right while recording the cumulative probabilities—that produces the CDF!
The PDF gives the probability density, the likelihood of the random variable falling close to a value. In comparison, the cumulative distribution function sums the probability densities leading up to each value.
In this manner, the probability density on a PDF is the rate of change for the CDF. Consequently, the ranges where the PDF curve has relatively high probability densities correspond to areas on the CDF curve with steeper slopes. Lower PDF densities correspond to shallower CDF slopes. As the PDF’s curve approaches its peak at the mean, the CDF’s slope increases to its maximum steepness. After the PDF’s peak, the CDF slope flattens.
Learn more about Empirical Cumulative Distribution Function Plots . These graphs help you compare an observed cumulative distribution to a fitted distribution.
Share this:

Reader Interactions
March 16, 2024 at 2:36 am
“A cumulative distribution function (CDF) and a probability distribution function (PDF)” may be a typo.
March 16, 2024 at 7:35 pm
Thank you, Sakurai! I’ve fixed that!
Comments and Questions Cancel reply

IMAGES
VIDEO
COMMENTS
Many statistical tests make the assumption that datasets are normally distributed. There are four common ways to check this assumption in R: 1. (Visual Method) Create a histogram. If the histogram is roughly "bell-shaped", then the data is assumed to be normally distributed. 2. (Visual Method) Create a Q-Q plot.
As n tends to infinity t-distribution tends to a Normal, therefore if n is sufficiently large (say > 60) you could approximate the t-distribution with a Normal one. Now, by fixing a certain alpha (confidence level), we decide to reject the null Hypothesis (H0) if: Where is the sample mean, the standard deviation and z the percentile of the ...
Parametric (normal distributions) R Function: t.test() Null hypothesis (H 0): The means of the sampled distribution matches the expected mean. History: William Sealy Gosset ; T-tests should only be used when the population is at least 20 times larger than its respective sample.
There are several methods for evaluate normality, including the Kolmogorov-Smirnov (K-S) normality test and the Shapiro-Wilk's test. The null hypothesis of these tests is that "sample distribution is normal". If the test is significant, the distribution is non-normal. Shapiro-Wilk's method is widely recommended for normality test and it ...
Examining A Single VariableStatistical Hypothesis Testing Q-Q Normal Plots TheQ-Q Normal Plotof A is then the Q-Q plot of A against the standard normal distribution. NOTE:This will be a straight line if the distribution of A is normal of any mean and standard deviation. Happily, there is an R function that does all of this: qqnorm.
6.2.2.1 Known Standard Deviation. It is simple to calculate a hypothesis test in R (in fact, we already implicitly did this in the previous section). When we know the population standard deviation, we use a hypothesis test based on the standard normal, known as a \(z\)-test.Here, let's assume \(\sigma_X = 2\) (because that is the standard deviation of the distribution we simulated from above ...
Intro to hypothesis testing. Hypothesis testing is all about answering the question: for a parameter \ ... Our null distribution is then \(\mathrm{Normal}(8, 2)\). Now that we have a null distribution, we need to dream up a test statistic. In this class, you'll always be given a test statistic. For now we'll use the T statistic.
HYPOTHESIS TESTING IN R. Hypothesis testing is a statistical procedure used to make decisions or draw conclusions about the characteristics of a population based on information provided by a sample. NORMALITY TESTS. Normality tests are used to evaluate whether a data sample follows a normal distribution. These tests allow to verify if the data ...
Here's a step-by-step procedure for generating and testing power using R: Install and load the pwr package: # Load the pwr package library ( pwr) #> Warning: package 'pwr' was built under R version 4.2.3. Define the parameters for power analysis.
We consider testing whether the population mean μμ is equal to m0m0 or not. Therefore, we can formulate the data and hypotheses as below: Data Y1, ⋯, Yniid ∼ Normal(μ, σ2) Hypotheses. H1: μ = m0H 1: μ = m0. H2: μ ≠ m0H 2: μ ≠ m0. Priors. We also need to specify priors for μμ under both hypotheses.
In the following tutorials, we demonstrate the procedure of hypothesis testing in R first with the intuitive critical value approach. Then we discuss the popular p-value approach as alternative. ... Normal Distribution; Chi-squared Distribution; Student t Distribution; F Distribution; Interval Estimation. Point Estimate of Population Mean;
The null hypothesis of these tests is that "sample distribution is normal". If the test is significant, the distribution is non-normal. Shapiro-Wilk's method is widely recommended for normality test and it provides better power than K-S. It is based on the correlation between the data and the corresponding normal scores.
Areas under the normal distribution in R and by hand. Now that we have covered the \(Z\) ... A normality test is a hypothesis test, so as the sample size increases, their capacity of detecting smaller differences increases. So as the number of observations increases, the Shapiro-Wilk test becomes very sensitive even to a small deviation from ...
A normality test is a hypothesis test, so as the sample size increases, their capacity of detecting smaller differences increases. So as the number of observations increases, the Shapiro-Wilk test becomes very sensitive even to a small deviation from normality. ... Areas under the normal distribution in R and by hand Now that we have covered ...
I am trying to calculate the p-values of observations by comparing them to the normal distribution in R using pnorm(). I have constructed a random distribution as my background model on which I would like to test the significance of various tests. I know for example, my background normal distribution has a mean of 1 and a standard deviation of 3.
Step #1: Stating the null and alternative hypothesis. Step #2: Computing the test statistic. Step #3: Computing the p -value. Step #4: Concluding and interpreting the results. Method C: Comparing the target parameter with the confidence interval. Step #1: Stating the null and alternative hypothesis.
In this section, we will check for normality in R using three different methods. These methods are the Shapiro-Wilks test, the Anderson-Darling test, and the Kolmogorov-Smirnov test. Each of these tests provides a way to assess whether a sample of data comes from a normal distribution.
5. @stackoverflowuser2010, Here are two definitive answers to your simple question: (1) You can never, no matter how much data you collect, conclusively determine that it was generated from an exactly normal distribution. (2) Your data is not generated from an exactly normal distribution (no real data is). - Ian Fellows.
In hypothesis testing, we start with a null hypothesis (H0) and an alternative hypothesis (H1). For a t-test, the null hypothesis is typically that there's no difference between the means of the two groups, while the alternative hypothesis is that there is a difference. In this example: H0: μ1 = μ2 (the means of Group 1 and Group 2 are equal)
Step 1: Check assumptions and write hypotheses. The assumption here is that the sampling distribution is approximately normal. From the given StatKey output, the randomization distribution is approximately normal. \ (H_0\colon p=0.50\) \ (H_a\colon p>0.50\) 2. Calculate the test statistic.
Asymptotic one-sample Kolmogorov-Smirnov test data: data D = 0.095166, p-value = 0.3255 alternative hypothesis: two-sided 3. Anderson-Darling Test. The Anderson-Darling test is a statistical test that determines if a dataset follows a specific distribution, notably the normal distribution. R
In a one-tailed test, the entire significance level is allocated to one tail of the distribution. For example, if you are using a significance level of 0.05 (5%), you would reject the null hypothesis if your data point falls in the 5% tail on either the right (for a right-tailed test) or the left (for a left-tailed test) end of the distribution.
The Shapiro-Wilk test can come to our rescue. There is also a Python library, called Scipy, with the implementation of this test, in which the null hypothesis is that the variable follows a normal distribution. We reject the hypothesis if the p-value is smaller or equal to the significance level (ex: 0.05).
statistics document from liberty university, 10 pages, hypothesis testing examples example 1 • with a sample of size n=250. use the pooled data to test whether the distribution of the percent wound healing is approximately normal. specifically, use the following distribution: 30%, 40%, 20% and 10% and =0.05
It is a cumulative function because it sums the total likelihood up to that point. Its output always ranges between 0 and 1. CDFs have the following definition: CDF (x) = P (X ≤ x) Where X is the random variable, and x is a specific value. The CDF gives us the probability that the random variable X is less than or equal to x.