statistics numerical problem solving

Teach yourself statistics

Statistics Problems

One of the best ways to learn statistics is to solve practice problems. These problems test your understanding of statistics terminology and your ability to solve common statistics problems. Each problem includes a step-by-step explanation of the solution.

• Use the dropdown boxes to describe the type of problem you want to work on.
• click the Submit button to see problems and solutions.

Main topic:

Problem description:

In one state, 52% of the voters are Republicans, and 48% are Democrats. In a second state, 47% of the voters are Republicans, and 53% are Democrats. Suppose a simple random sample of 100 voters are surveyed from each state.

What is the probability that the survey will show a greater percentage of Republican voters in the second state than in the first state?

The correct answer is C. For this analysis, let P 1 = the proportion of Republican voters in the first state, P 2 = the proportion of Republican voters in the second state, p 1 = the proportion of Republican voters in the sample from the first state, and p 2 = the proportion of Republican voters in the sample from the second state. The number of voters sampled from the first state (n 1 ) = 100, and the number of voters sampled from the second state (n 2 ) = 100.

The solution involves four steps.

• Make sure the sample size is big enough to model differences with a normal population. Because n 1 P 1 = 100 * 0.52 = 52, n 1 (1 - P 1 ) = 100 * 0.48 = 48, n 2 P 2 = 100 * 0.47 = 47, and n 2 (1 - P 2 ) = 100 * 0.53 = 53 are each greater than 10, the sample size is large enough.
• Find the mean of the difference in sample proportions: E(p 1 - p 2 ) = P 1 - P 2 = 0.52 - 0.47 = 0.05.

σ d = sqrt{ [ P1( 1 - P 1 ) / n 1 ] + [ P 2 (1 - P 2 ) / n 2 ] }

σ d = sqrt{ [ (0.52)(0.48) / 100 ] + [ (0.47)(0.53) / 100 ] }

σ d = sqrt (0.002496 + 0.002491) = sqrt(0.004987) = 0.0706

z p 1 - p 2 = (x - μ p 1 - p 2 ) / σ d = (0 - 0.05)/0.0706 = -0.7082

Using Stat Trek's Normal Distribution Calculator , we find that the probability of a z-score being -0.7082 or less is 0.24.

Therefore, the probability that the survey will show a greater percentage of Republican voters in the second state than in the first state is 0.24.

See also: Difference Between Proportions

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons

Margin Size

• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

1.01: Introduction to Numerical Methods

• Last updated
• Save as PDF
• Page ID 126380

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)

( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

\( \newcommand{\Span}{\mathrm{span}}\)

\( \newcommand{\id}{\mathrm{id}}\)

\( \newcommand{\kernel}{\mathrm{null}\,}\)

\( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\)

\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\)

\( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)

\( \newcommand{\vectorA}[1]{\vec{#1}}      % arrow\)

\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}}      % arrow\)

\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vectorC}[1]{\textbf{#1}} \)

\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)

\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)

\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)

Lesson 1: Why Numerical Methods?

Learning objectives.

After successful completion of this lesson, you should be able to: 1) Enumerate the need for numerical methods.

Introduction

Numerical methods are techniques to approximate mathematical processes (examples of mathematical processes are integrals, differential equations, nonlinear equations).

Approximations are needed because

1) we cannot solve the procedure analytically, such as the standard normal cumulative distribution function

\[\Phi(x) = \frac{1}{\sqrt{2\pi}}\int_{- \infty}^{x}e^{- t^{2}/2}{dt} \;\;\;\;\;\;\;\;\;\;\;\;(\PageIndex{1.1}) \nonumber\]

2) the analytical method is intractable, such as solving a set of a thousand simultaneous linear equations for a thousand unknowns for finding forces in a truss (Figure \(\PageIndex{1.1}\)).

In the case of Equation (1), an exact solution is not available for \(\Phi(x)\) other than for \(x = 0\) and \(x \rightarrow \infty\) . For other values of \(x\) where an exact solution is not available, one may solve the problem by using approximate techniques such as the left-hand Reimann sum you were introduced to in the Integral Calculus course.

In the truss problem, one can solve \(1000\) simultaneous linear equations for \(1000\) unknowns without using a calculator. One can use fractions, long divisions, and long multiplications to get the exact answer. But just the thought of such a task is laborious. The task may seem less laborious if we are allowed to use a calculator, but it would still fall under the category of an intractable, if not an impossible, problem. So, we need to find a numerical technique and convert it into a computer program that solves a set of \(n\) equations and \(n\) unknowns.

Again, what are numerical methods? They are techniques to solve a mathematical problem approximately. As we go through the course, you will see that numerical methods let us find solutions close to the exact one, and we can quantify the approximate error associated with the answer. After all, what good is an approximation without quantifying how good the approximation is?

Audiovisual Lecture

Title: Why Do We Need Numerical Methods

Summary : This video is an introduction to why we need numerical methods.

Lesson 2: Steps of Solving an Engineering Problem

After successful completion of this lesson, you should be able to:

1) go through the stages (problem description, mathematical modeling, solving and implementation) of solving a particular physical problem.

Numerical methods are used by engineers and scientists to solve problems. However, numerical methods are just one step in solving an engineering problem. There are four steps for solving an engineering problem, as shown in Figure \(\PageIndex{2.1}\).

The first step is to describe the problem. The description would involve writing the background of the problem and the need for its solution. The second step is developing a mathematical model for the problem, and this could include the use of experiments or/and theory. The third step involves solving the mathematical model. The solution may consist of analytical or/and numerical means. The fourth step is implementing the solution to see if the problem is solved.

Let us see through an example of these four steps of solving an engineering problem.

Problem Description

To make the fulcrum (Figure \(\PageIndex{2.2}\)) of a bascule bridge, a long hollow steel shaft called the trunnion is shrunk-fit into a steel hub. The resulting steel trunnion-hub assembly is then shrunk-fit into the girder of the bridge.

The shrink-fitting is done by first immersing the trunnion in a cold medium such as a dry-ice/alcohol mixture. After the trunnion reaches the steady-state temperature, that is, the temperature of the cold medium, the outer diameter of the trunnion contracts. The trunnion is taken out of the medium and slid through the hole of the hub (Figure \(\PageIndex{2.3}\)).

When the trunnion heats up, it expands and creates an interference fit with the hub. In 1995, on one of the bridges in Florida, this assembly procedure did not work as designed. Before the trunnion could be inserted fully into the hub, the trunnion got stuck. Luckily, the trunnion was taken out before it got stuck permanently. Otherwise, a new trunnion and hub would need to be ordered at the cost of \(\$50,000\) . Coupled with construction delays, the total loss could have been more than a hundred thousand dollars.

Why did the trunnion get stuck? Because the trunnion had not contracted enough to slide through the hole. Can you find out why this happened?

Simple Mathematical Model

A hollow trunnion of an outside diameter \(12.363^{\prime\prime}\) is to be fitted in a hub of inner diameter \(12.358^{\prime\prime}\) . The trunnion was put in a dry ice/alcohol mixture (temperature of the fluid - dry-ice/alcohol mixture is \(- 108{^\circ}\text{F}\) ) to contract the trunnion so that it can be slid through the hole of the hub. To slide the trunnion without sticking, a diametrical clearance of at least \(0.01^{\prime\prime}\) is required between the trunnion and the hub. Assuming the room temperature is \(80{^\circ}\text{F}\) , is immersing the trunnion in a dry-ice/alcohol mixture a correct decision?

To calculate the contraction in the diameter of the trunnion, the thermal expansion coefficient at room temperature is used. In that case, the reduction \(\Delta D\) in the outer diameter of the trunnion is

\[\displaystyle\Delta D = D\alpha\Delta T \;\;\;\;\;\;\;\;\;\;\;\; (\PageIndex{2.1}) \nonumber\]

\[D = \text{ outer diameter of the trunnion,} \nonumber\]

\[\alpha = \text{ coefficient of thermal expansion coefficient at room temperature, and} \nonumber\]

\[\Delta T = \text{change in temperature.} \nonumber\]

Solution to Simple Mathematical Model

\[D = 12.363^{\prime\prime} \nonumber\]

\[\alpha = 6.47 \times 10^{-6}\ \text{in/in/}^{\circ}\text{F} \text{ at } 80{^\circ}\text{F} \nonumber\]

\[\displaystyle \begin{split} \Delta T&= T_{\text{fluid}} - T_{\text{room}}\\ &= - 108 - 80\\ &= - 188{^\circ}\ \text{F}\end{split} \nonumber\]

\[T_{\text{fluid}}= \text{ temperature of dry-ice/alcohol mixture} \nonumber\]

\[T_{\text{room}}= \text{ room temperature} \nonumber\]

the reduction in the outer diameter of the trunnion from Equation \((\PageIndex{2.1})\) hence is given by

\[\begin{split} \Delta D &= (12.363)\left( 6.47 \times 10^{- 6} \right)\left( - 188 \right)\\ &=- 0.01504^{\prime\prime} \end{split} \nonumber\]

So the trunnion is predicted to reduce in diameter by \(0.01504^{\prime\prime}\) . But is this enough reduction in diameter? As per specifications, the trunnion diameter needs to change by

\[\begin{split} \Delta D &= -\text{trunnion outside diameter} + \text{hub inner diameter} - \text{diametric clearance}\\ &= -12.363 +12.358 - 0.01\\ &= - 0.015^{\prime\prime} \end{split} \nonumber\]

So, according to this calculation, immersing the steel trunnion in dry-ice/alcohol mixture gives the desired contraction of greater than \(0.015^{\prime\prime}\) as the predicted contraction is \(0.01504^{\prime\prime}\) . But, when the steel trunnion was put in the hub, it got stuck. Why did this happen? Was our mathematical model adequate for this problem, or did we create a mathematical error?

Accurate Mathematical Model

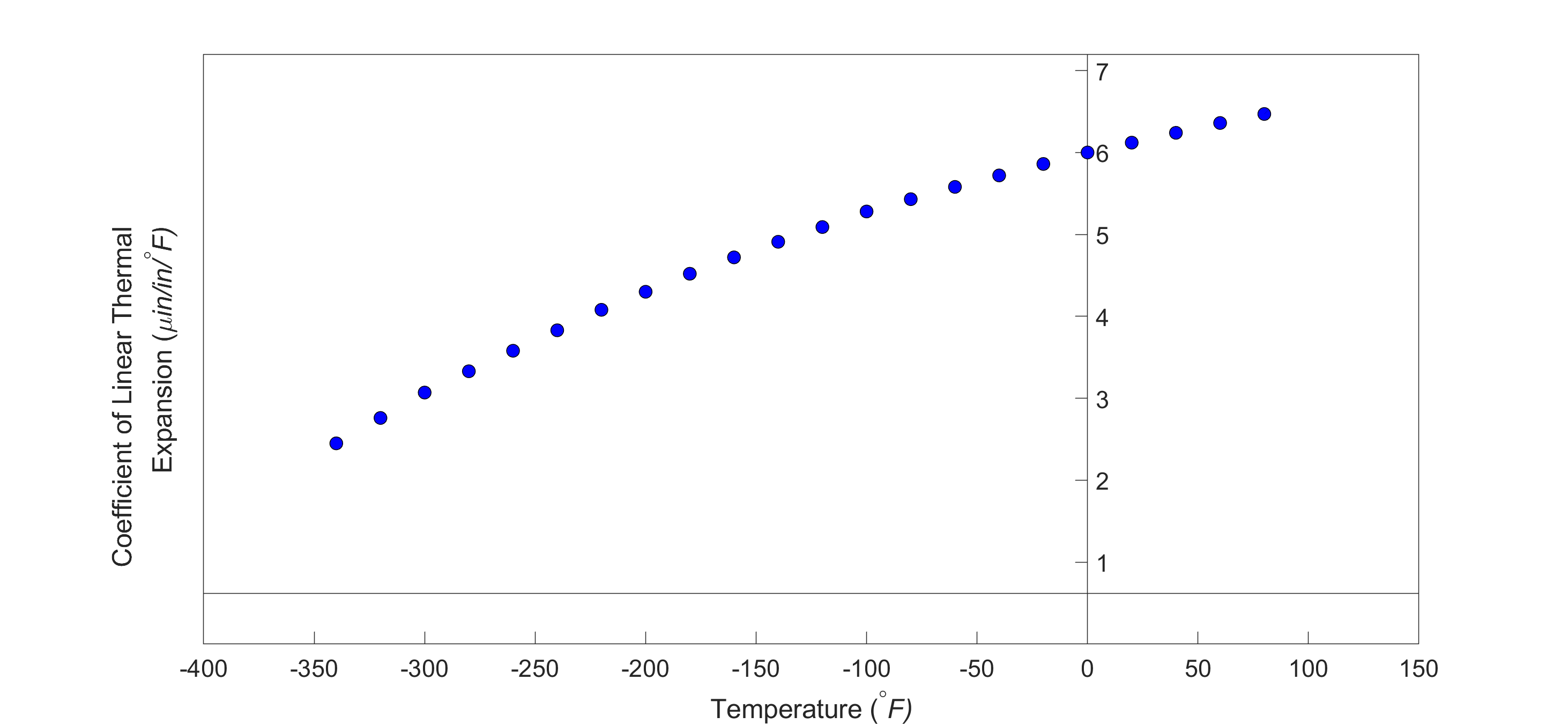
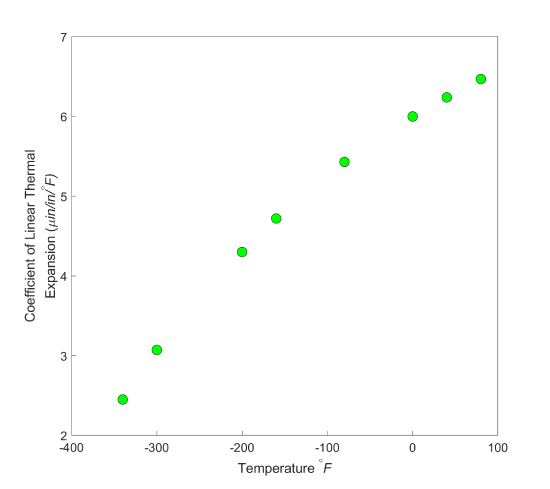
As shown in Figure \(\PageIndex{2.4}\) and Table 1, the thermal expansion coefficient of steel decreases with temperature and is not constant over the range of temperature the trunnion goes through. Hence, Equation \((\PageIndex{2.1})\) would overestimate the thermal contraction.

he contraction in the diameter of the trunnion for which the thermal expansion coefficient varies as a function of temperature is given by

\[ \Delta D = D\int_{T_{\text{room}}}^{T_{\text{fluid}}} \alpha dT \;\;\;\;\;\;\;\;\;\;\;\; (\PageIndex{2.2}) \nonumber\]

Solution to More Accurate Mathematical Model

So, one needs to curve fit the data to find the coefficient of thermal expansion as a function of temperature. This curve is found by regression where we best fit a function to the data given in Table 1. In this case, we may fit a second-order polynomial

\[\displaystyle\alpha = a_{0} + a_{1} T + a_{2} T^{2}\;\;\;\;\;\;\;\;\;\;\;\; (\PageIndex{2.3}) \nonumber\]

The values of the coefficients in the above Equation \((\PageIndex{2.3})\) will be found by polynomial regression (we will learn how to do this later in the chapter on Nonlinear Regression). At this point, we are just going to give you these values, and they are

\[\begin{bmatrix} a_{0} \\ a_{1} \\ a_{2} \\ \end{bmatrix} = \begin{bmatrix} 6.0150 \times 10^{- 6} \\ 6.1946 \times 10^{- 9} \\ - 1.2278 \times 10^{- 11} \\ \end{bmatrix} \nonumber\]

to give the polynomial regression model (Figure \(\PageIndex{2.5}\)) as

\[\displaystyle \begin{split} \alpha &= a_{0} + a_{1}T + a_{2}T^{2}\\ &= {6.0150} \times {1}{0}^{- 6} + {6.1946} \times {10}^{- 9}T - {1.2278} \times {10}^{- {11}}T^{2} \end{split} \;\;\;\;\;\;\;\;\;\;\;\; (\PageIndex{2.4}) \nonumber\]

Knowing the values of \(a_{0}\) , \(a_{1}\) , and \(a_{2}\) , we can then find the contraction in the trunnion diameter from Equations \((\PageIndex{2.2})\) and \((\PageIndex{2.3})\) as

\[\begin{split} \displaystyle\Delta D &= D\int_{T_{\text{room}}}^{T_{\text{fluid}}}{(a_{0} + a_{1}T + a_{2}T^{2}}){dT}\\ &= D\left\lbrack a_{0}T + a_{1}\frac{T^{2}}{2} + a_{2}\frac{T^{3}}{3} \right\rbrack\begin{matrix} T_{\text{fluid}} \\ \\ T_{\text{room}} \\ \end{matrix}\\ &= D\lbrack a_{0}(T_{\text{fluid}} - T_{\text{room}}) + a_{1}\frac{({T_{\text{fluid}}}^{2} - {T_{\text{room}}}^{2})}{2}\\ & \ \ \ \ \ + a_{2}\frac{({T_{\text{fluid}}}^{3} - {T_{\text{room}}}^{3})}{3}\rbrack\;\;\;\;\;\;\;\;\;\;\;\;(\PageIndex{2.5}) \end{split} \nonumber\]

Substituting the values of the variables gives

\[\displaystyle \begin{split} \Delta D &= 12.363\begin{bmatrix} 6.0150 \times 10^{- 6} \times ( - 108 - 80) \\ + 6.1946 \times 10^{- 9}\displaystyle \frac{\left( ( - 108)^{2} - (80)^{2} \right)}{2} \\ - 1.2278 \times 10^{- 11}\displaystyle \frac{(( - 108)^{3} - (80)^{3})}{3} \\ \end{bmatrix}\\ &= - 0.013689^{\prime\prime}\end{split} \nonumber\]

What do we find here? The contraction in the trunnion is not enough to meet the required specification of \(0.015^{\prime\prime}\) .

Implementing the Solution

Although we were able to find out why the trunnion got stuck in the hub, we still need to find and implement a solution. What if the trunnion were immersed in a medium that was cooler than the dry-ice/alcohol mixture of \(- 108{^\circ}F\) , say liquid nitrogen, which has a boiling temperature of \(- 321{^\circ}F\) ? Will that be enough for the specified contraction in the trunnion?

As given in Equation \((\PageIndex{2.5})\)

\[\displaystyle \begin{split} \Delta D &= D\int_{T_{\text{room}}}^{T_{\text{fluid}}}{(a_{0} + a_{1}T + a_{2}T^{2}}){dT}\\ &= D\left\lbrack a_{0}T + a_{1}\frac{T^{2}}{2} + a_{2}\frac{T^{3}}{3} \right\rbrack\begin{matrix} T_{\text{fluid}} \\ \\ T_{\text{room}} \\ \end{matrix}\\ &= D\lbrack a_{0}(T_{\text{fluid}} - T_{\text{room}}) + a_{1}\frac{({T_{\text{fluid}}}^{2} - {T_{\text{room}}}^{2})}{2}\\ & \ \ \ \ \ + a_{2}\frac{({T_{\text{fluid}}}^{3} - {T_{\text{room}}}^{3})}{3}\rbrack\;\;\;\;\;\;\;\;\;\;\;\; (\PageIndex{2.5}-repeated) \end{split} \nonumber\]

which gives

\[\displaystyle \begin{split} \Delta D &= 12.363\begin{bmatrix} 6.0150 \times 10^{- 6} \times ( - 321 - 80) \\ + 6.1946 \times 10^{- 9} \displaystyle\frac{\left( ( - 321)^{2} - (80)^{2} \right)}{2} \\ \ - 1.2278 \times 10^{- 11} \displaystyle\frac{(( - 321)^{3} - (80)^{3})}{3} \\ \end{bmatrix}\\ & \\ &= - 0.024420^{\prime\prime} \end{split} \nonumber\]

The magnitude of this contraction is larger than the specified value of \(0.015^{\prime\prime}\).

So here are some questions that you may want to ask yourself later in the course.

1) What if the trunnion were immersed in liquid nitrogen (boiling temperature \(= - 321{^\circ}\text{F}\) )? Will that cause enough contraction in the trunnion?

2) Rather than regressing the thermal expansion coefficient data to a second-order polynomial so that one can find the contraction in the trunnion OD, how would you use the trapezoidal rule of integration for unequal segments?

3) What is the relative difference between the two results?

4) We chose a second-order polynomial for regression. Would a different order polynomial be a better choice for regression? Is there an optimum order of polynomial we could use?

Title: Steps of Solving Engineering Problems

Summary : This video teaches you the steps of solving an engineering problem- define the problem, model the problem, solve, and implementation of the solution.

Lesson 3: Overview of Mathematical Processes Covered in This Course

1) enumerate the seven mathematical processes for which numerical methods are used.

Numerical methods are techniques to approximate mathematical processes. This introductory numerical methods course will develop and apply numerical techniques for the following mathematical processes:

1) Roots of Nonlinear Equations

2) Simultaneous Linear Equations

3) Curve Fitting via Interpolation

4) Differentiation

5) Curve Fitting via Regression

6) Numerical Integration

7) Ordinary Differential Equations.

Some undergraduate courses in numerical methods may include topics of partial differential equations, optimization, and fast Fourier transforms as well.

Roots of a Nonlinear Equation

The ubiquitous formula

\[ x = \frac{- b \pm \sqrt{b^2 - 4ac}}{2a} \;\;\;\;\;\;\;\;\;\;\;\; (\PageIndex{3.1}) \nonumber\]

of finding the roots of a quadratic equation \(\displaystyle ax^{2} + bx + c = 0\) goes back to the ancient world. But in the real world, we get equations that are not just the quadratic ones. They can be polynomial equations of a higher order and transcendental equations.

Take an example of a floating ball shown in Figure \(\PageIndex{3.1}\), where you are asked to find the depth to which the ball will get submerged when floating in the water.

Assume that the ball has a density of \(600\ \text{kg}/\text{m}^{3}\) and has a radius of \(0.055\ \text{m}\) . On applying the Newtons laws of motion and hence equating the weight of the ball to the buoyancy force, one finds that the depth, \(x\) in meters, to which the ball is underwater and is given by

\[\displaystyle 3.993 \times 10^{- 4} - 0.165x^{2} + x^{3} = 0 \;\;\;\;\;\;\;\;\;\;\;\; (\PageIndex{2}) \nonumber\]

Equation \((\PageIndex{3.2})\) is a cubic equation that you will need to solve. The equation will have three roots, and the root that is between \(0\ \text{m}\) (just touching the water surface) and \(0.11\ \text{m}\) (almost submerged) would be the depth to which the ball is submerged. The two other roots would be physically unacceptable. Note that a cubic equation with real coefficients can have a set of one real root and two complex roots or a set of three real roots. You may wonder, why could such an application be important? Let’s suppose you are filling in this tank with water, and you are using this ball as a control so that when the ball goes all the way to the top that the flow of the water stops – say in a fish tank that needs replenishing while the owner is away for a few weeks. So, we do need to figure out how much of the ball is submerged underwater.

A cubic equation can be solved exactly by radicals, but it is a tedious process. The same is true but even more complicated for a general fourth-order polynomial equation as well. However, there is no closed-form solution available for a general polynomial equation of fifth-order or more. So, one has to resort to numerical techniques to solve polynomial and other transcendental nonlinear equations (e.g., finding the nonzero roots of \(\tan x = x\) ).

Simultaneous Linear Equations

Ever since you were exposed to algebra, you have been solving simultaneous linear equations.

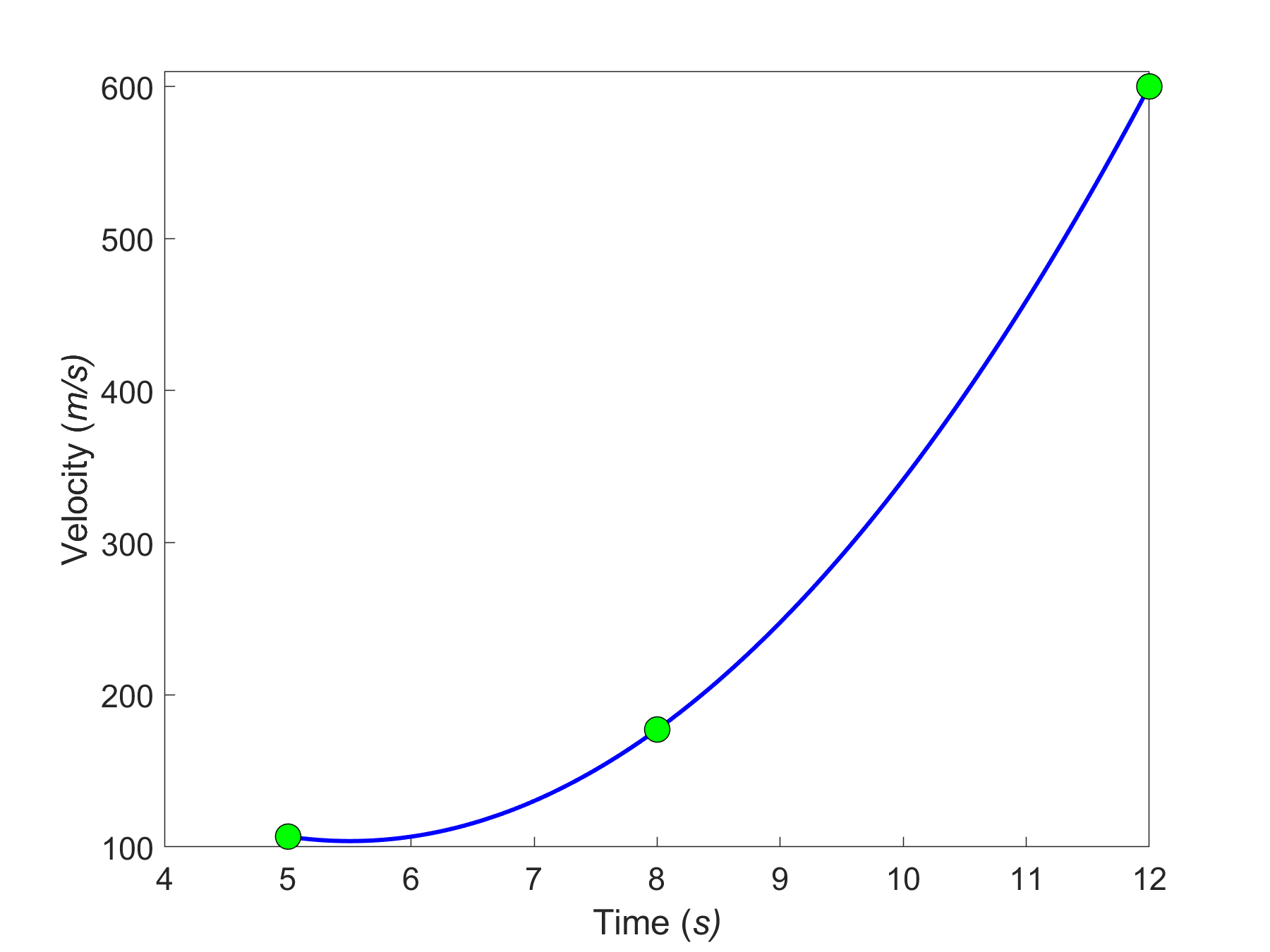
Take this problem statement as an example. Suppose the upward velocity of a rocket (Figure \(\PageIndex{3.2}\)) is given at three different times (Table \(\PageIndex{3.1}\)).

The velocity data is approximated by a polynomial as

\[\displaystyle v\left( t \right) = at^{2} + {bt} + c\ {, 5} \leq t \leq {12}.\;\;\;\;\;\;\;\;\;\;\;\;(\PageIndex{3.3}) \nonumber\]

To estimate the velocity at a time that is not given to us, we can set up the equations to find the coefficients \(a,b,c\) of the velocity profile.

The polynomial in Equation (3) is going through three data points \(\left( t_{1},v_{1} \right),\left( t_{2},v_{2} \right),\) and \(\left( t_{3},v_{3} \right)\) where from Table 1.1.3.1

\[\begin{split} t_{1} &= 5,v_{1} = 106.8\\ t_{2} &= 8,v_{2} = 177.2\\ t_{3} &= 12,v_{3} = 600.0 \end{split} \nonumber\]

Requiring that \(v\left( t \right) = at^{2} + bt + c\) passes through the three data points, gives

\[\begin{split} v\left( t_{1} \right) &= v_{1} = at_{1}^{2} + bt_{1} + c\\ v\left( t_{2} \right) &= v_{2} = at_{2}^{2} + bt_{2} + c\\ v\left( t_{3} \right) &= v_{3} = at_{3}^{2} + bt_{3} + c \end{split} \nonumber\]

Substituting the data \(\left( t_{1},\ v_{1} \right),\ \left( t_{2},\ v_{2} \right),\) and \(\left( t_{3},\ v_{3} \right)\) gives

\[\begin{split} a\left( 5^{2} \right) + b\left( 5 \right) + c = 106.8 \\ a\left( 8^{2} \right) + b\left( 8 \right) + c = 177.2 \\ a\left( 12^{2} \right) + b\left( 12 \right) + c = 600.0 \end{split} \nonumber\]

\[\begin{split} 25a + 5b + c = 106.8 \\ 64a + 8b + c = 177.2 \\ 144a + 12b + c = 600.0 \end{split} \;\;\;\;\;\;\;\;\;\;\;\; (\PageIndex{3.4}) \nonumber\]

Solving a few simultaneous linear equations such as the above set can be done without the knowledge of numerical techniques. However, imagine that instead of three given points, you were given 10 data points. Now the setting up as well as solving the set of 10 simultaneous linear equations without numerical techniques becomes laborious, if not impossible.

Curve Fitting by Interpolation

Interpolation involves that given a function as a set of data points. How does one find the value of the function at points that are not given?. For this, we choose a function, called an interpolant, and make it pass through all the points involved.

You may think that you have already used interpolation in courses such as Thermodynamics and Statistics. After all, it was just taking two points from a table at the back of the textbook or online and finding the value of the function at a point in between by using a straight line.

Take this problem statement as an example. Let’s suppose the upward velocity of a rocket is given at three different times (Table 1.1.3.1).

If one asked you to estimate the velocity at \(7\ \text{s}\) , one might simply use the straight-line formula you are most accustomed to as given below.

Given ( \(t_{1},\ v_{1}\) ) and ( \(t_{2},\ v_{2}\) ), the value of the function \(v\) at \(t\) is given by

\[\displaystyle v = v_{1} + \frac{v_{2} - v_{1}}{t_{2} - t_{1}}(t - t_{1}) \;\;\;\;\;\;\;\;\;\;\;\; (\PageIndex{3.5}) \nonumber\]

Although this is possibly enough for courses such as Thermodynamics and Statistics, there are two questions to ask. Is the value calculated accurately, and how accurate is it? To know that, one needs to calculate at least more than one value. In the above example of a rocket velocity vs. time, one can instead use a second-order polynomial interpolant and set up the three equations and three unknowns to find the unknown coefficients, \(a\) , \(b\) , and \(c\) as given in the previous section.

\[v\left( t \right) = at^{2} + {bt} + c{ ,\ 5} \leq t \leq {12}\;\;\;\;\;\;\;\;\;\;\;\; (\PageIndex{3.6}) \nonumber\]

Then, the resulting second-order polynomial can be used to find the velocity at \(t = 7\ \text{s}\) .

The value obtained from the second-order polynomial (Equation \((\PageIndex{3.6})\)) can be considered to be a new measure of the value of \(v( 7)\) , and the first-order polynomial (Equation \((\PageIndex{3.5})\)) result can be used to determine the accuracy of the results.

Numerical Differentiation

You have taken a semester-long course in Differential Calculus, where you found derivatives of continuous functions. So let’s suppose somebody gives you the velocity of a rocket as a continuous and at least once differentiable function of time and wants you to find acceleration. Indeed for this particular problem, you can use your differential calculus knowledge to differentiate the velocity function to get the acceleration and put in the value of time, \(t = 7\ \text{s}\) . What if the velocity vs. time is not given as a continuous and at least once differentiable function? Instead, let’s say the function is given at discrete data points (Table 1.1.3.1). How are you then going to find out what the acceleration at \(t = 7\ \text{s}\) ? Do we draw a straight line from \((5,106.8)\) to \((8,177.2)\) and use the straight-line slope as the estimate of acceleration? How do we know that this is adequate? We could incorporate all three points and find a second-order polynomial as given by Equation \((\PageIndex{3.6})\). This polynomial can now be differentiated to estimate the acceleration at \(t = 7\ \text{s}\) . Now the two values can be used to evaluate the accuracy of the calculated acceleration.

Curve Fitting by Regression

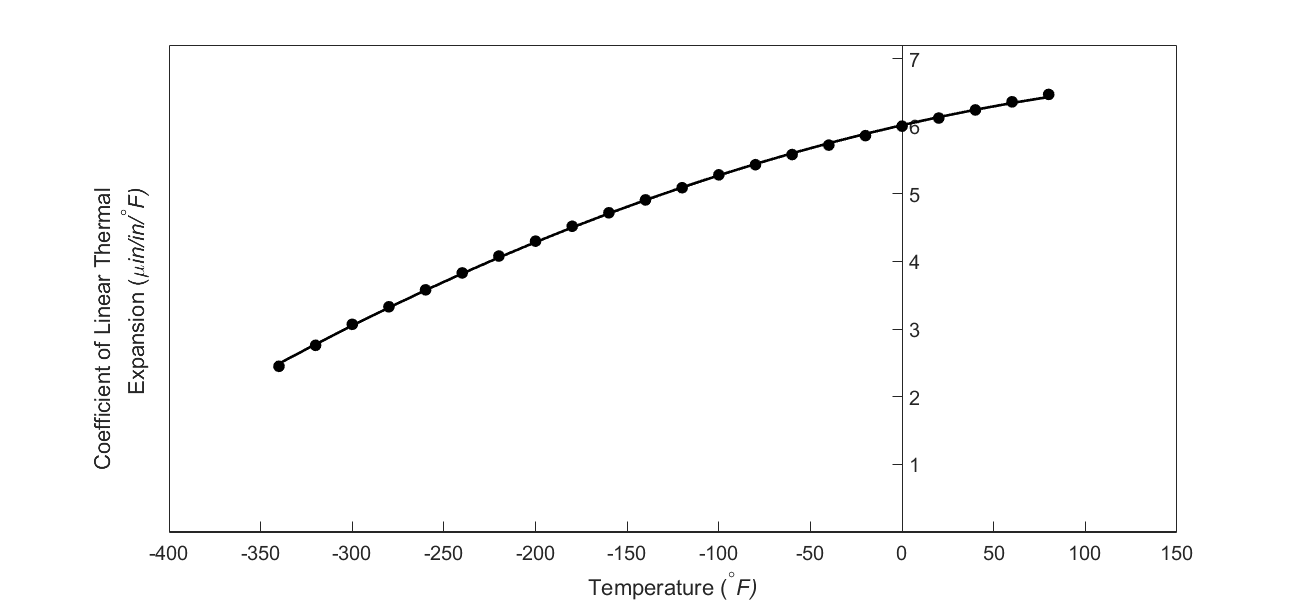
When we talked about curve fitting by interpolation, the chosen interpolant needs to go through all the points considered. What happens when we are given many data points, and we instead want a simplified formula to explain the relationship between two variables. See, for example, in Figure \(\PageIndex{3.4a}\), we are given the coefficient of linear thermal expansion data for cast steel as a function of temperature. Looking at the data, one may proclaim that a straight line could explain the data, and that is drawn in Figure \(\PageIndex{3.4b}\). How we draw this straight line is what is called regression. It would be based on minimizing some form of the residuals between what is observed (given data points) and what is predicted (straight line). It does not mean that every time you have data given to you, you draw a straight line. It is possible that a second-order polynomial or a transcendental function other than the first-order polynomial will be a better representation of this particular data. So these are the questions that we will answer when we discuss regression. We will also discuss the adequacy of linear regression models.

Numerical Integration

You have taken a whole course on integral calculus. Now, why would we need to make numerical approximations of integrals? Just like the standard normal cumulative distribution function

\[\displaystyle\Phi(x) = \frac{1}{\sqrt{2\pi}}\int_{- \infty}^{x}e^{- t^{2}/2}{dt} \;\;\;\;\;\;\;\;\;\;\;\; (\PageIndex{3.7}) \nonumber\]

cannot be solved exactly, or when the integrand values are given at discrete data points, we need to use numerical methods of integration.

In the previous lesson, we looked at the example of contracting the diameter of a trunnion for a bascule bridge fulcrum assembly by dipping it in a mixture of dry ice and alcohol. The contraction is given by

\[\Delta D = D\int_{T_{\text{room}}}^{T_{\text{fluid}}}{\alpha\ dT} \;\;\;\;\;\;\;\;\;\;\;\; (\PageIndex{3.8}) \nonumber\]

\[D = \text{outer diameter of the trunnion,} \nonumber\]

\[\alpha = \text{coefficient of linear thermal expansion that is varying with temperature} \nonumber\]

\[T_{\text{room}}= \text{room temperature} \nonumber\]

\[T_{\text{fluid}}= \text{temperature of dry-ice alcohol mixture.} \nonumber\]

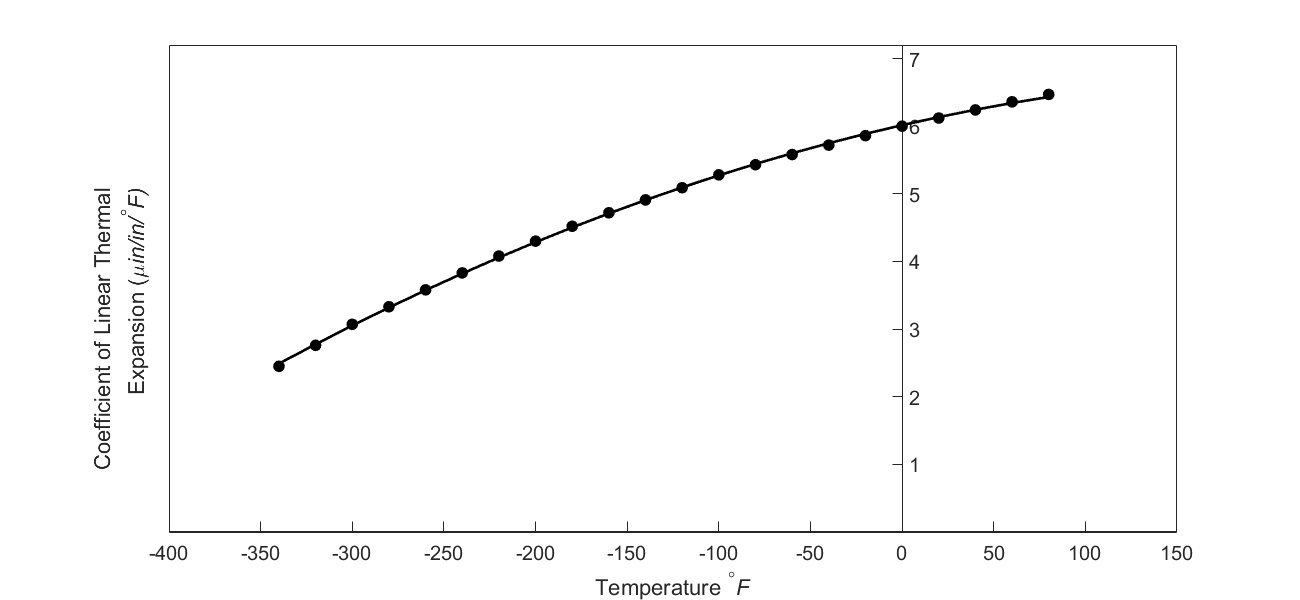
From Figure \(\PageIndex{3.4a}\), one can note that the coefficient of thermal expansion is only given at discrete temperatures and not as a known continuous function that could be integrated exactly. So we have to resort to numerical methods by approximating the data, say, by a second-order polynomial obtained via regression.

In Figure \(\PageIndex{3.6}\), the thermal expansion coefficient of typical cast steel is approximated by a second-order regression polynomial as given by Equation \((\PageIndex{3.9}\)) (how we get this is a later lesson in regression) as

\[\displaystyle\alpha = - 1.2278 \times 10^{- 11}T^{2} + 6.1946 \times 10^{- 9}T + 6.0150 \times 10^{- 6} \;\;\;\;\;\;\;\;\;\;\;\; (\PageIndex{3.9}) \nonumber\]

The contraction of the diameter then is given by

\[\displaystyle\Delta D = D\int_{T_{\text{room}}}^{T_{\text{fluid}}}{\left( - 1.2278 \times 10^{- 11}T^{2} + 6.1946 \times 10^{- 9}T + 6.015 \times 10^{- 6} \right){dT}} \;\;\;\;\;\;\;\; (\PageIndex{3.10}) \nonumber\]

and can now be calculated using integral calculus.

Numerical Solution of Ordinary Differential Equations

Taking the same example of the trunnion being dipped in a dry-ice/alcohol mixture, one could ask the question - What would the temperature of the trunnion be after dipping it in the mixture for 30 minutes? The model is given by an ordinary differential equation for the temperature \(\theta\) as a function of time, \({t.}\)

\[\displaystyle -{hA} \left(\theta - \theta_{a} \right) = {mC} \frac{d \theta}{dt}\;\;\;\;\;\;\;\;\;\;\;\; (\PageIndex{3.11}) \nonumber\]

\[h= \text{the convective cooling coefficient,}\ \text{W/m}^{2} \cdot \text{K} \nonumber\]

\[A = \text{surface area},\ \text{m}^2 \nonumber\]

\[\theta_{a} = \text{ambient temperature of dry-ice/alcohol mixture},\ \text{K} \nonumber\]

\[m = \text{mass of the trunnion, kg} \nonumber\]

\[C = \text{specific heat of the trunnion,}\ \text{J/(kg} \cdot \text{K)} \nonumber\]

The differential Equation \((\PageIndex{3.11})\) can be solved exactly by using the classical solution, Laplace transform, or separation of variables techniques. So, where do numerical methods enter into the picture for this problem? For the temperature range of room temperatures to cold media such as dry-ice/alcohol, several of the variables in Equation \((\PageIndex{3.11})\) are not constant but change with the temperature. These include the convection coefficient \(h\) as well as the specific heat \(C\) . Now, this differential equation has turned nonlinear as follows.

\[\displaystyle -h(\theta)A\left( \theta - \theta_{a} \right) = mC(\theta)\frac{d \theta}{dt} \;\;\;\;\;\;\;\;\;\;\;\; (\PageIndex{3.12}) \nonumber\]

The ordinary differential Equation \((\PageIndex{3.12})\) cannot be solved by exact methods and would need to be solved by a numerical method.

In the above discussion, we have illustrated the need for numerical methods for each of the seven mathematical processes in the course. In the lessons to follow, we will be developing various numerical techniques to approximate the mathematical processes to calculate acceptable accurate values while calculating associated errors.

Title: Overview of Mathematical Processes Covered in This Course

Summary : This lecture shows you four mathematical procedures that need numerical methods - namely, nonlinear equations, differentiation, simultaneous linear equations, and interpolation.

Multiple Choice Test

(1). Solving an engineering problem requires four steps. In order of sequence, the four steps are

(A) formulate, model, solve, implement

(B) formulate, solve, model, implement

(C) formulate, model, implement, solve

(D) model, formulate, implement, solve

(2). One of the roots of the equation \(x^{3} - 3x^{2} + x - 3 = 0\) is

(C) \(\sqrt{3}\)

(3). The solution to the set of equations

\[\begin{split} 25a + b + c &= 25 \\ 64a + 8b + c &= 71\\ 144a + 12b + c &= 155 \end{split} \nonumber\]

most nearly is \(\left( a,b,c \right) =\)

(A) \((1,1,1)\)

(B) \((1,-1,1)\)

(C) \((1,1,-1)\)

(D) does not have a unique solution.

(4). The exact integral of \(\displaystyle \int_{0}^{\frac{\pi}{4}} 2 \cos 2x \ dx\) is most nearly

(A) \(-1.000\)

(B) \(1.000\)

(C) \(0.000\)

(D) \(2.000\)

(5). The value of \(\displaystyle \frac{dy}{dx}\left( 1.0 \right)\) , given \(y = 2\sin\left( 3x \right)\), is most nearly

(A) \(-5.9399\)

(B) \(-1.980\)

(C) \(0.31402\)

(D) \(5.9918\)

(6). The form of the exact solution of the ordinary differential equation \(\displaystyle 2\frac{dy}{dx} + 3y = 5e^{- x},\ y\left( 0 \right) = 5\) is

(A) \(Ae^{- 1.5x} + Be^{x}\)

(B) \(Ae^{- 1.5x} + Be^{- x}\)

(C) \(Ae^{1.5x} + Be^{- x}\)

(D) \(Ae^{- 1.5x} + Bxe^{- x}\)

For complete solution, go to

http://nm.mathforcollege.com/mcquizzes/01aae/quiz_01aae_introduction_answers.pdf

Problem Set

(1). Give one example of an engineering problem where each of the following mathematical procedures is used. If possible, draw from your experience in other classes or from any professional experience you have gathered to date.

a) Differentiation

b) Nonlinear equations

c) Simultaneous linear equations

d) Regression

e) Interpolation

f) Integration

g) Ordinary differential equations

(2). Only using your nonprogrammable calculator, find the root of

\[x^{3} - 0.165x^{2} + 3.993 \times 10^{- 4} = 0 \nonumber\]

by any method. Hint: Find one root by hit and trial, and use long division for factoring the polynomial.

\(0.06237758151,\ 0.1463595047,\ -0.04373708621\)

(3). Solve the following system of simultaneous linear equations by any method

\[\begin{split} 25a + 5b + c &= 106.8\\ 64a + 8b + c &= 177.2\\ 144a + 12b + c &= 279.2 \end{split} \nonumber\]

\(a = 0.2904761905,\ b = 19.69047619,\ c = 1.085714286\)

(4). You are given data for the upward velocity of a rocket as a function of time in the table below. Find the velocity at \(t = 16 \ \text{s}\) .

\(543.0420000\ \text{m/s}\)

(5). Integrate exactly.

\[\int_{0}^{\pi/2}\sin2x \ dx \nonumber\]

\[\frac{dy}{dx}(x = 1.4) \nonumber\]

\[y = e^{x} + \sin(x) \nonumber\]

\(4.225167110\)

(7). Solve the following ordinary differential equation exactly.

\[\frac{dy}{dx} + y = e^{- x}, \ y(0) = 5 \nonumber\]

Also find \(y(0),\ \displaystyle \frac{dy}{dx}\ (0),\ y(2.5),\ \displaystyle\frac{dy}{dx}\ (2.5)\)

\(\displaystyle y(0)=5,\ \frac{dy}{dx}(0)=-4,\ y(2.5)=0.61563,\ \frac{dy}{dx}(2.5)=-0.53355\)

If you're seeing this message, it means we're having trouble loading external resources on our website.

If you're behind a web filter, please make sure that the domains *.kastatic.org and *.kasandbox.org are unblocked.

To log in and use all the features of Khan Academy, please enable JavaScript in your browser.

Unit 7: Medium: Problem solving and data analysis

About this unit.

This unit tackles the medium-difficulty problem solving and data analysis questions on the SAT Math test. Work through each skill, taking quizzes and the unit test to level up your mastery progress.

Ratios, rates, and proportions: medium

• Ratios, rates, and proportions | SAT lesson (Opens a modal)
• Ratios, rates, and proportions — Basic example (Opens a modal)
• Ratios, rates, and proportions — Harder example (Opens a modal)
• Ratios, rates, and proportions: medium Get 3 of 4 questions to level up!

Unit conversion: medium

• Unit conversion | Lesson (Opens a modal)
• Units — Basic example (Opens a modal)
• Units — Harder example (Opens a modal)
• Unit conversion: medium Get 3 of 4 questions to level up!

Percentages: medium

• Percentages | Lesson (Opens a modal)
• Percents — Basic example (Opens a modal)
• Percents — Harder example (Opens a modal)
• Percentages: medium Get 3 of 4 questions to level up!

Center, spread, and shape of distributions: medium

• Center, spread, and shape of distributions | Lesson (Opens a modal)
• Center, spread, and shape of distributions — Basic example (Opens a modal)
• Center, spread, and shape of distributions — Harder example (Opens a modal)
• Center, spread, and shape of distributions: medium Get 3 of 4 questions to level up!

Data representations: medium

• Data representations | Lesson (Opens a modal)
• Key features of graphs — Basic example (Opens a modal)
• Key features of graphs — Harder example (Opens a modal)
• Data representations: medium Get 3 of 4 questions to level up!

Scatterplots: medium

• Scatterplots | Lesson (Opens a modal)
• Scatterplots — Basic example (Opens a modal)
• Scatterplots — Harder example (Opens a modal)
• Scatterplots: medium Get 3 of 4 questions to level up!

Linear and exponential growth: medium

• Linear and exponential growth | Lesson (Opens a modal)
• Linear and exponential growth — Basic example (Opens a modal)
• Linear and exponential growth — Harder example (Opens a modal)
• Linear and exponential growth: medium Get 3 of 4 questions to level up!

Probability and relative frequency: medium

• Probability and relative frequency | Lesson (Opens a modal)
• Table data — Basic example (Opens a modal)
• Table data — Harder example (Opens a modal)
• Probability and relative frequency: medium Get 3 of 4 questions to level up!

Data inferences: medium

• Data inferences | Lesson (Opens a modal)
• Data inferences — Basic example (Opens a modal)
• Data inferences — Harder example (Opens a modal)
• Data inferences: medium Get 3 of 4 questions to level up!

Evaluating statistical claims: medium

• Evaluating statistical claims | Lesson (Opens a modal)
• Data collection and conclusions — Basic example (Opens a modal)
• Data collection and conclusions — Harder example (Opens a modal)
• Evaluating statistical claims: medium Get 3 of 4 questions to level up!

How to Solve Statistical Problems Efficiently [Master Your Data Analysis Skills]

• November 17, 2023

Are you tired of feeling overstimulated by statistical problems? Welcome – you have now found the perfect article.

We understand the frustration that comes with trying to make sense of complex data sets.

Let’s work hand-in-hand to unpack those statistical secrets and find clarity in the numbers.

Do you find yourself stuck, unable to move forward because of statistical roadblocks? We’ve been there too. Our skill in solving statistical problems will help you find the way in through the toughest tough difficulties with confidence. Let’s tackle these problems hand-in-hand and pave the way to success.

As experts in the field, we know what it takes to conquer statistical problems effectively. This article is adjusted to meet your needs and provide you with the solutions you’ve been searching for. Join us on this voyage towards mastering statistics and unpack a world of possibilities.

Key Takeaways

• Data collection is the foundation of statistical analysis and must be accurate.
• Understanding descriptive and inferential statistics is critical for looking at and interpreting data effectively.
• Probability quantifies uncertainty and helps in making smart decisionss during statistical analysis.
• Identifying common statistical roadblocks like misinterpreting data or selecting inappropriate tests is important for effective problem-solving.
• Strategies like understanding the problem, choosing the right tools, and practicing regularly are key to tackling statistical tough difficulties.
• Using tools such as statistical software, graphing calculators, and online resources can aid in solving statistical problems efficiently.

Understanding Statistical Problems

When exploring the world of statistics, it’s critical to assimilate the nature of statistical problems. These problems often involve interpreting data, looking at patterns, and drawing meaningful endings. Here are some key points to consider:

• Data Collection: The foundation of statistical analysis lies in accurate data collection. Whether it’s surveys, experiments, or observational studies, gathering relevant data is important.
• Descriptive Statistics: Understanding descriptive statistics helps in summarizing and interpreting data effectively. Measures such as mean, median, and standard deviation provide useful ideas.
• Inferential Statistics: This branch of statistics involves making predictions or inferences about a population based on sample data. It helps us understand patterns and trends past the observed data.
• Probability: Probability is huge in statistical analysis by quantifying uncertainty. It helps us assess the likelihood of events and make smart decisionss.

To solve statistical problems proficiently, one must have a solid grasp of these key concepts.

By honing our statistical literacy and analytical skills, we can find the way in through complex data sets with confidence.

Let’s investigate more into the area of statistics and unpack its secrets.

Identifying Common Statistical Roadblocks

When tackling statistical problems, identifying common roadblocks is important to effectively find the way in the problem-solving process.

Let’s investigate some key problems individuals often encounter:

• Misinterpretation of Data: One of the primary tough difficulties is misinterpreting the data, leading to erroneous endings and flawed analysis.
• Selection of Appropriate Statistical Tests: Choosing the right statistical test can be perplexing, impacting the accuracy of results. It’s critical to have a solid understanding of when to apply each test.
• Assumptions Violation: Many statistical methods are based on certain assumptions. Violating these assumptions can skew results and mislead interpretations.

To overcome these roadblocks, it’s necessary to acquire a solid foundation in statistical principles and methodologies.

By honing our analytical skills and continuously improving our statistical literacy, we can adeptly address these tough difficulties and excel in statistical problem-solving.

For more ideas on tackling statistical problems, refer to this full guide on Common Statistical Errors .

Strategies for Tackling Statistical Tough difficulties

When facing statistical tough difficulties, it’s critical to employ effective strategies to find the way in through complex data analysis.

Here are some key approaches to tackle statistical problems:

• Understand the Problem: Before exploring analysis, ensure a clear comprehension of the statistical problem at hand.
• Choose the Right Tools: Selecting appropriate statistical tests is important for accurate results.
• Check Assumptions: Verify that the data meets the assumptions of the chosen statistical method to avoid skewed outcomes.
• Consult Resources: Refer to reputable sources like textbooks or online statistical guides for assistance.
• Practice Regularly: Improve statistical skills through consistent practice and application in various scenarios.
• Seek Guidance: When in doubt, seek advice from experienced statisticians or mentors.

By adopting these strategies, individuals can improve their problem-solving abilities and overcome statistical problems with confidence.

For further ideas on statistical problem-solving, refer to a full guide on Common Statistical Errors .

Tools for Solving Statistical Problems

When it comes to tackling statistical tough difficulties effectively, having the right tools at our disposal is important.

Here are some key tools that can aid us in solving statistical problems:

• Statistical Software: Using software like R or Python can simplify complex calculations and streamline data analysis processes.
• Graphing Calculators: These tools are handy for visualizing data and identifying trends or patterns.
• Online Resources: Websites like Kaggle or Stack Overflow offer useful ideas, tutorials, and communities for statistical problem-solving.
• Textbooks and Guides: Referencing textbooks such as “Introduction to Statistical Learning” or online guides can provide in-depth explanations and step-by-step solutions.

By using these tools effectively, we can improve our problem-solving capabilities and approach statistical tough difficulties with confidence.

For further ideas on common statistical errors to avoid, we recommend checking out the full guide on Common Statistical Errors For useful tips and strategies.

Putting in place Effective Solutions

When approaching statistical problems, it’s critical to have a strategic plan in place.

Here are some key steps to consider for putting in place effective solutions:

• Define the Problem: Clearly outline the statistical problem at hand to understand its scope and requirements fully.
• Collect Data: Gather relevant data sets from credible sources or conduct surveys to acquire the necessary information for analysis.
• Choose the Right Model: Select the appropriate statistical model based on the nature of the data and the specific question being addressed.
• Use Advanced Tools: Use statistical software such as R or Python to perform complex analyses and generate accurate results.
• Validate Results: Verify the accuracy of the findings through strict testing and validation procedures to ensure the reliability of the endings.

By following these steps, we can streamline the statistical problem-solving process and arrive at well-informed and data-driven decisions.

For further ideas and strategies on tackling statistical tough difficulties, we recommend exploring resources such as DataCamp That offer interactive learning experiences and tutorials on statistical analysis.

• Recent Posts

• Razer Keyboard: Using Without the Software [Discover the Surprising Answer] - May 21, 2024
• Do Senior Software Engineers Do Coding Interviews? [Master Your Interview Skills Now] - May 21, 2024
• Master Python for Data Science: Unleash Machine Learning Power [Boost Your Skills Now] - May 21, 2024

• Request new password
• Create a new account

Statistics with R

Student resources, chapter 3: descriptive statistics: numerical methods.

1. A sample contains the following data values: 1.50, 1.50, 10.50, 3.40, 10.50, 11.50, and 2.00. What is the mean? Create an object named E3_1; apply the mean() function.

#Comment1. Use the c() function; read data values into object E3_1. E3_1 <- c(1.50, 1.50, 10.50, 3.40, 10.50, 11.50, 2.00) #Comment2. Use the mean() function to find the mean. mean(E3_1) ## [1]  5.842857

Answer: The mean is 5.843.

2. Find the median of the sample (above) in two ways: (a) use the median() function to find it directly, and (b) use the sort() function to locate the middle value visually.

#Comment1. Use the median() function to find the median. median(E3_1) ##  [1]  3.4 #Comment2. Use the sort() function to arrange data values in #ascending order. sort(E3_1) ## [1] 1.5 1.5 2.0 3.4 10.5 10.5 11.5

Answer: The median of a data set is the middle value when the data items are arranged in ascending order. Once the data values have been sorted into ascending order (we have done this above using the sort() function) it is clear that the middle value is 3.4 since there are 3 values to the left of 3.4 and 3 values to the right. Alternatively, the function median() can be used to find the median directly.

3. Create a vector with the following elements: -37.7, -0.3, 0.00, 0.91, e , π , 5.1, 2e and 113,754, where e is the base of the natural logarithm (roughly 2.718282...) and the ratio of a circle's diameter to its radius (about 3.141593...). Name the object E3_ 2. What are the median and the mean? The 78th percentile? What are the variance and the standard deviation? Note that R understands exp(1) as e , pi as π .

#Comment1. Use the c() function to create the object E3_2. E3_2 <- c(-37.7, -0.3, 0.00, 0.91, exp(1), pi, 5.1, 2*exp(1), 113754) #Comment2. Use the mean() function to find the mean. mean(E3_2) ## [1] 12637.03 #Comment3. Use the median() function to find the median. median(E3_2) ## [1] 2.718282 #Comment4. Use the quantile() function with prob = c(0.78) #to find the 78th percentile. quantile(E3_2, prob = c(0.78)) ## 78% ## 5.180775 #Comment5. Use the var() function to find the variance. var(E3_2) ## [1] 1437840293 #Comment6. Use the sd() function to find the standard deviation. sd(E3_2) ## [1] 37918.86

Answer: The mean is 12,637.03; the median is 2.718282..., or e . Since the data values in E3_ 2 are arranged in ascending order, the median is easily identifed as the middle value, e (or 2.718282...), since there are four values below and four values above. Moreover, simply summing all nine data values, and dividing by nine, provides the mean. The 78th percentile is reported as 5.180775; the variance and standard deviation are 1,437,840,293 and 37,918.86, respectively.

4. Consider the following data values: 10, 20, 30, 40, 50, 60, 70, 80, 90, and 100. What are the 10th and 90th percentiles? Hint: use function seq(from=,to=,by=) to create the data set. Name the data set E3_3.

#Comment1. Use the seq(from =, to =, by =) function to create #object E3_3 E3_3 <- seq(from = 10, to = 100, by = 10) #Comment2. Examine the contents of E3_3 to make sure it contains #the desired elements. E3_3 ## [1] 10 20 30 40 50 60 70 80 90 100 #Comment3. Use the quantile() function to find the 10th and 90th #percentiles. Remember to use probs=c(0.1, 0.9) quantile(E3_3, probs = c(0.1, 0.9)) ## 10% 90% ## 19 91

Answer: The 10th and 90th percentiles are 19 and 91, respectively. Note that the 10th percentile (19) is a value which exceeds at least 10% of items in the data set; the 90th percentile (91) is a value which exceeds at least 90% of the items. Note also that it is possible to define any percentiles by setting the values in the probs=c() argument of the quantiles() function.

5. What is the median of E3_3? Find the middle value visually and with the median() function.

#Comment. Use function median() to find the median. median(E3_3) ## [1] 55

Answer: This data set has an even number of values, all arranged in ascending order. Accordingly, the median is found by taking the average of the values in the two middle positions: the average of 50 (the value in the 5th position) and 60 (the value in the 6th position) is 55.

6. The mode is the value that occurs with greatest frequency in a set of data, and it is used as one of the measures of central tendency. Consider a sample with these nine values: 5, 1, 3, 9, 7, 1, 6, 11, and 8. Does the mode provide a measure of central tendency similar to that of the mean? The median?

#Comment1. Use the c() function and read the data into object E3_4. E3_4 <- c(5, 1, 3, 9, 7, 1, 6, 11, 8) #Comment2. Use the table() function to create a frequency #distribution. table(E3_4) ## E3_4 ##    1    3   5    6   7   8   9  11 ##    2    1   1    1   1   1   1   1 #Comment3. Use the mean() and median() functions to find the #mean and median of E3_4. mean(E3_4) ## [1] 5.666667 median(E3_4) ## [1] 6

Answer: Since the value of the mode in this instance is 1 (it appears twice), it provides less insight into the central tendency of this sample than does the mean (5.667) or the median (6).

7. Consider another sample with these nine values: 5, 1, 3, 9, 7, 4, 6, 11, and 8. How well does the mode capture the central tendency of this sample?

Answer: Since all the data items appear only once, there is no single value for the mode; there are nine modes, one for each data value.

8. Find the 90th percentile, the 1st, 2nd, and 3rd quartiles as well as the minimum and maximum values of the LakeHuron data set (which is part of the R package and was used in the Chapter 1 in-text  exercises). What is the mean? What is the median?

#Comment1. Use the quantile() function with prob=c(). quantile(LakeHuron, prob = c(0.00, 0.25, 0.50, 0.75, 0.90, 1.00))

##  0%                25%      50%         75%           90%        100% ##  575.960   578.135   579.120   579.875    580.646   581.860

#Comment2. Use the mean() function to find the mean.

mean(LakeHuron)

## [1] 579.0041

#Comment3. Use the median() function to find the median.

median(LakeHuron)

## [1] 579.12

Answer: The minimum value (the 0 percentile) is 575.960 and the maximum value (the 100th percentile) is 581.860; the 1st, 2nd, and 3rd quartiles are 578.135, 579.120, and 579.875, respectively. The median (also known as the 2nd quartile or the 50th percentile) is 579.120. The mean is 579.0041 while the 90th percentile is 580.646.

9. Find the range, the interquartile range, the variance, the standard deviation, and the coefficient of variation of the LakeHuron data set.

#Comment1. Find the range by subtracting min() from max(). max(LakeHuron) - min(LakeHuron) ## [1] 5.9 #Comment2. Use the IQR() function to find the interquartile range. IQR(LakeHuron) ## [1] 1.74 #Comment3. Use the var() function to find the variance. var(LakeHuron) ## [1] 1.737911 #Comment4. Use the sd() function to find the standard deviation. sd(LakeHuron) ## [1] 1.318299 #Comment5. To find the coefficient of variation, find sd()/mean(). sd(LakeHuron) / mean(LakeHuron) ## [1] 0.002276838

Answer: The range is 5.9 feet and the interquartile range is 1.74 feet. Moreover, the variance and standard deviation are 1.737911 and 1.318299 feet, respectively. Finally, the coeffcient of variation is 0.002276838; that is, the standard deviation is only about 0.228% of the mean.

10. What are the range and interquartile range for the following data set: -37.7, -0.3, 0.00, 0.91, e, π , 5.1, 2 e and 113,754? Note that this is the same data set as that used above where we named it E3_2.

#Comment1. To find range, subtract min() from max(). max(E3_2) - min(E3_2) ## [1] 113791.7 #Comment 2. To find interquartile range, use IQR() function. IQR(E3_2) ## [1] 5.1

Answer: The range is 113,791.7; the interquartile range is 5.1. The great difference between these two measures of dispersion results from the fact that the interquartile range provides the range of the middle 50% of the data while the range includes all data values, including the outliers.

11.Using the vectorization capability of R, find the sample variance and sample standard deviation of the data set E3_3 (used above). (This exercise provides the opportunity to write and execute some basic R code for the purpose of deriving the variance and standard deviation of a simple data set.) Check both answers against those using the var() and sd() functions. Recall that the expression for the sample variance is

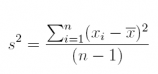
#Comment1. Use mean() to find mean of E3_3; assign to xbar. xbar <- mean(E3_3) #Comment2. Find the deviations about the mean; assign to devs . devs <- (E3_3 - xbar) #Comment3. Find the squared deviations about the mean; assign #the result to sqrd.devs. sqrd.devs <- (devs) ^ 2 #Comment4. Sum the squared deviations about the mean; assign #result to the object sum.sqrd.devs . sum.sqrd.devs <- sum(sqrd.devs) #Comment5. Divide the sum of squared deviations by (n-1) #to find the variance; assign result to the object variance. variance <- sum.sqrd.devs / (length(E3_3) - 1) #Comment6. Examine the contents of variance. variance ## [1] 916.6667 #Comment7. The standard deviation is the positive square root #of the variance; assign result to the object standard.deviation. standard.deviation <- sqrt(variance) #Comment8. Examine the contents of standard.deviation. standard.deviation ## [1] 30.2765 #Comment9. Use the var() function to find the variance. var(E3_3)

## [1] 916.6667 #Comment10. Use the sd() function to find the standard #deviation. sd(E3_3) ## [1] 30.2765

Answer: The variance is 916.6667; the standard deviation is 30.2765. The answers reported by var() and sd() equal those produced by way of vectorization.

12. The temps data set (available on the companion website) includes the high-and-low temperatures (in degrees Celsius) for April 1, 2016 of ten major European cities; import the data set into an object named E3_5. What is the covariance of the high and low temperatures? What does the covariance tell us?

Answer: The covariance of the two variables is 37.28889. Although it is difficult to learn very much from the value of the covariance of the two variables, we do know that the two variables are positively related. This is an unsurprising nding because the cities having the warmest daytime temperatures are also those that have the warmest nighttime temperatures.

#Comment1. Read data set temps into the object named E3_5. E3_5 <- temps #Comment2. Use the head(,3) function to find out the variable names. head(E3_5, 3) ##               City        Daytemp   Nighttemp ##        1   Athens          21             12 ##       2    Barcelona     12              9 ##       3    Dublin             6             1 #Comment3. Use the cov() function to find the covariance. The #variable names are Daytemp and Nighttemp. cov(E3_5$Daytemp, E3_5$Nighttemp) ## [1] 37.28889

13. To gain practice using R, calculate the covariance of the two variables in the temps data (available on the companion website). Do not use the function cov(). Recall that the sample covariance between two variables x and y is:

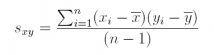
#Comment1. Find the deviations between each observation #on Daytemp and its mean. Name resulting object devx. devx <- (E3_5$Daytemp - mean(E3_5$Daytemp)) #Comment2. Find the deviations between each observation #on Nighttemp and its mean. Name resulting object devy. devy <- (E3_5$Nighttemp - mean(E3_5$Nighttemp)) #Comment3. Find product of devx and devy; name result crossproduct. crossproduct <- devx * devy #Comment4. Find the covariance by dividing crossproduct by (n-1), # or 9. Assign the result to object named covariance. covariance <- sum(crossproduct) / (length(E3_5$Daytemp) - 1) #Comment5. Examine contents of covariance. Confirm that it is #the same value as that found in previous exercise. covariance ## [1] 37.28889

14. There are several ways we might explore the relationship between two variables. In the next few exercises, we analyze the daily_ idx_ chg data set (available on the companion website) to explore the pros and cons of several of those methods. The data set itself consists of the percent daily change (from the previous trading day) of the closing numbers for two different widely-traded stock indices, the Dow Jones Industrial Average and the S&P500, for all trading days from April 2 to April 30, 2012. Comment on the data. What is the covariance of the price movements for the two indices? What does the covariance tell us about the relationship between the two variables? As a first step, import the data into an object named E3_6.

#Comment1. Read the daily_idx_chg data into the object E3_6. E3_6 <- daily_idx_chg

#Comment2. Use the summary() function to identify the variable names #and to acquire a feel for what the data look like. summary(E3_6) ##        PCT.DOW.CHG                 PCT.SP.CHG ##        Min. :-1.6500                     Min. :-1.7100 ##        1st Qu.:-0.6675                 1st Qu.:-0.6525 ##        Median : 0.0350                 Median :-0.0550 ##        Mean : 0.0045                    Mean :-0.0340 ##        3rd Qu.: 0.6075                  3rd Qu.: 0.6875 ##        Max. : 1.5000                      Max. : 1.5500 #Comment3. Use the cov() function to find the covariance. cov(E3_6) ##                             PCT.DOW.CHG  PCT.SP.CHG ## PCT.DOW.CHG      0.7542682          0.7693505 ## PCT.SP.CHG          0.7693505           0.8562042

Answer: The two variable names are PCT.DOW.CHG and PCT.SP.CHG; the data values seem to be centered around 0 with values ranging from around 1.55 to -1.71 The covariance is 0.7693505 which tells us only that the two variables are positively related.

15. Standardize the daily_idx_chg data and re-calculate the covariance. Is it the same?

#Comment1. Use the scale() function to standardize the data. #Assign the result to the object named std_indices . std_indices <- scale(E3_6) #Comment2. Use the cov() function to find the covariance. cov(std_indices) ##                             PCT.DOW.CHG  PCT.SP.CHG ## PCT.DOW.CHG    1.0000000           0.9573543 ## PCT.SP.CHG         0.9573543          1.0000000

Answer: The covariance is 0.9573543. No, the covariance is not the same, even though it has been applied to the same data. In fact, the covariance on raw data does not (in general) equal the covariance on the same data when standardized.

16. Find the correlation of the two variables in the daily _idx_ chg data.

#Comment. Use the cor() function to find the correlation. cor(E3_6) ##                             PCT.DOW.CHG   PCT.SP.CHG ##  PCT.DOW.CHG   1.0000000           0.9573543 ##  PCT.SP.CHG        0.9573543           1.0000000

Answer: The correlation is 0.9573543, exactly the same as the covariance of the standardized variables. In general, the correlation of two unstandardized variables equals the covariance of the same two variables in standardized form.

17. Standardize the daily _idx_ chg data and re-calculate the correlation. Is it the same?

#Comment. Use the cor() function to find the correlation. cor(std_indices) ##                                 PCT.DOW.CHG      PCT.SP.CHG ##    PCT.DOW.CHG      1.0000000             0.9573543 ##    PCT.SP.CHG           0.9573543            1.0000000

Answer: The correlation between the standardized values is exactly the same as the correlation between the unstandardized values: 0.9573543. While the covariance is a ected by how the data are scaled—making it more dicult to interpret—the correlation is not a affected.

18. Make a scatter plot of the daily idx_ chg_ data with PCT.DOW.CHG on the horizontal axis, PCT.SP.CHG on the vertical. Add a main title and labels for the horizontal and vertical axes. Does the scatter plot con rm the positive linear association suggested by the correlation coeffcient?

#Comment. Use the plot() function to produce the scatter p lot. plot(E3_6$PCT.DOW.CHG, E3_6$PCT.SP.CHG,

xlab ='Percentage Daily Change in the Dow', ylab ='Percentage Daily Change in the S&P500', pch = 19, col ='purple', main ='A Plot of Daily Percent Changes in the Dow and S&P500')

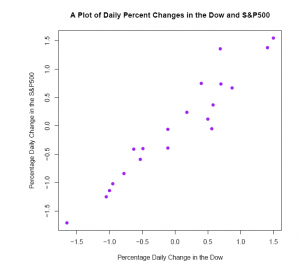
Answer: The scatter plot is consistent with a correlation coefficient of 0.9573543. There is a strongly positive linear association between the two stock market indices.

19. Below we have a curvilinear relationship where the points can be connected with a smooth, parabolic curve. See scatter plot. Which is the most likely correlation coefficient describing this relationship? -0.90, -0.50, -0.10, 0.00, +0.10, +0.50, or +0.90. (In the next four exercises, the code producing the scatter plots is included.)

x <- c(0, -1, -2, -3, -4) y <- c(4, 2, 1, 2, 4) data <- data.frame(X = x, Y = y) plot(data$X, data$Y, pch = 19, xlab ='x', ylab ='y')

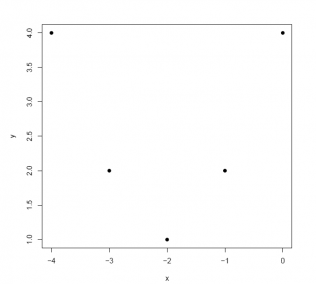
Answer: The correlation coefficient is 0.00.

cor(data$X, data$Y) ## [1] 0 Despite the points being scattered in a way characterized by a curvilinear relationship, the correlation coefficient describes the strength of the linear relationship between two variables. Just because a correlation coecient is zero does not mean that there is no relationship between the two variables. As we see in this case, there may be a relationship that is curvilinear rather than linear.

20. Which is the most likely correlation coefficient describing the relationship below? See the scatter plot. -0.90, -0.50, -0.10, 0.00, +0.10, +0.50, or +0.90.

x <- c(16, 13, 8, 6, 5)

y <- c(15, 20, 25, 25, 30)

data <- data.frame(X = x, Y = y)

plot(data$X, data$Y, pch = 19, xlab ='x', ylab ='y')

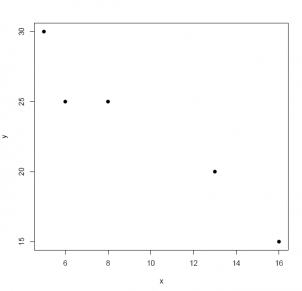
Answer: -0.90 is the closest value that the correlation coefficient might take: the relationship between the two variables is not only negative, it is linear as well. In fact, the correlation coefficient is -0.9657823.

cor(data$X, data$Y) ## [1] -0.9657823

21. Which is the most likely correlation coefficient describing the relationship below? -0.90, -0.50, -0.10, 0.00, +0.10, +0.50, or +0.90?

x <- c(24, 22, 22, 21, 19) y <- c(27, 24, 23, 21, 19) data <- data.frame(X = x, Y = y) plot(data$X, data$Y, pch = 19, xlab ='x', ylab ='y')

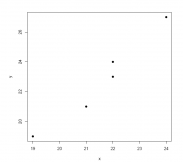
Answer: +0.90 is the closest value that the correlation coefficient might take: the relationship between the two variables is not only positive, it is linear as well. cor(data$X, data$Y) ## [1] 0.9800379 In fact, the correlation coefficient is +0.9800379.

22. Which is the most likely correlation coefficient describing the relationship below? -0.90, -0.50, -0.10, 0.00, +0.10, +0.50, or +0.90.

x <- c(0, -30, -30, -30, -60) y <- c(-20, 10, -20, -50, -20) data <- data.frame(X = x, Y = y) plot(data$X, data$Y, pch = 19, xlab ='x', ylab ='y')

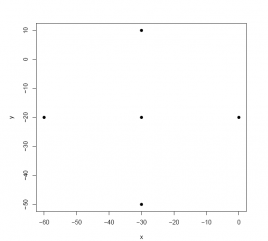
Answer: Although there is a pattern of points in the scatter diagram, there is no discernable linear relationship. In fact, the correlation coefficient is 0.00. cor(data$X, data$Y) ## [1] 0

23. The Empirical Rule states that approximately 68% of values of a normally-distributed variable fall in the interval from 1 standard deviation below the mean to 1 standard deviation above the mean. (A slightly more precise percentage is 68.269%.) Verify this claim by (a) generating n = 1, 000, 000 normally-distributed values with a mean of 100 and standard deviation of 15, and then (b) "counting" the number of data values that fall in this interval. If this claim is true, then approximately (0.68269)(1, 000, 000) = 682, 690 values should fall in the interval from 85 to 115; roughly (0.15866)(1, 000, 000) = 158, 655 below 85; and approximately (0.15866)(1, 000, 000) = 158, 655 values above 115. Use the rnorm(1000000,100,15) function.

#Comment1. Use the rnorm() function to generate n=1,000,000 #normally-distributed data values with a mean of 100 and standard #deviation of 15; name the resulting object normal_data. normal_data <- rnorm(1000000, 100, 15) #Comment2. Count the number of data values in the object named #normal_data that are at least 1 standard deviation below the #mean (that is, at least 15 below 100, or 85). Name this value a .

a <- length(which(normal_data <= 85)) #Comment3. Examine the contents of a to confirm that it is near #15.866 percent of 1,000,000, or roughly 158,666. a ## [1] 158607 #Comment4. Count the number of data values in the object named #normal_data that are at least 1 standard deviation above the #mean (that is, at least 15 above 100, or 115). Name this value b . b <- length(which(normal_data >= 115)) #Comment5. Examine the contents of b to confirm that it is near #15.866 percent of 1,000,000, or roughly 158,666. b ## [1] 158334 #Comment6. Calculate the proportion of 1,000,000 data items that #fall in the interval from 1 standard deviation below the mean to #1 standard deviation above the mean. Name that proportion c. c <- (1000000 - (a + b)) / 1000000 #Comment7. Examine the contents of c. To ensure that we understand #how c is calculated, plug the values for a (Comment3) and b #(Comment5) into the expression for c (Comment6). c ## [1] 0.683059 Using the data generation capability of R, we can confirm that the proportion of data values falling in the interval from one standard deviation below the mean to one standard deviation above the mean is approximately 68% .

24. The Empirical Rule also tells us that approximately 95% of values of a normally- distributed variable fall in the interval from 2 standard deviations below the mean to 2 standard deviations above the mean . (A more precise percentage is 95.45%.) Verify this claim. If this claim is true, then approximately (0.9545)(1, 000, 000) = 954, 500 values should fall in the interval from 70 to 130; roughly (0,02275)(1, 000, 000) = 22, 750 below 70; and approximately (0.02775)(1, 000, 000) = 22, 750 above 130.

#Comment1. Count the number of data values in normal_data that #are at least 2 standard deviations below the mean (that is, at #least 30 below 100, or 70); name this object a. a <- length(which(normal_data <= 70)) #Comment2. Examine the contents of a. Is it near 22,750? a ## [1] 22762 #Comment3. Count the number of data values in normal_data that #are at least 2 standard deviations above the mean (that is, at #least 30 above 100, or 130); name this object b. b <- length(which(normal_data >= 130)) #Comment4. Examine the contents of b. Is it near 22,750? b ## [1] 22717 #Comment5. Calculate the proportion of 1,000,000 data items that #fall in the interval from 2 standard deviations below the mean to #2 standard deviations above the mean. Name that proportion c. c <- (1000000 - (a + b)) / 1000000 #Comment6. Examine the contents of c. Is it near 0.9545? c ## [1] 0.954521 The proportion of data values falling in the interval from two standard deviations below the mean to two standard deviations above the mean is approximately 95:45%.

25. Use the R data generation function to draw n = 1, 000, 000 values from a uniform distribution that runs from a = 75 to b = 125; import the 1,000,000 data values into an object named uniform_data.

To help you envision uniformly-distributed data running between 75 and 125, see the histogram below. Also, see the Chapter 2 Appendix for an example of how the runif() function is used to simulate data values.

#Comment1. Use the runif() function to generate n=1,000,000 #uniformly-distributed data values over the interval from 75 to #125; name the resulting object uniform_data. uniform_data <- runif(1000000, 75, 125) #Comment2. To visualize how the data values are distributed, #use the hist() function to create a picture of the distribution. hist(uniform_data,

breaks = 50, xlim = c(70, 130), ylim = c(0, 25000), col ='blue')

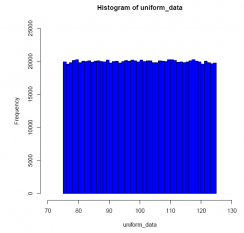
What is the proportion of values that falls in the interval from 90 to 110?

Answer:  From this simulation exercise, we see that the proportion of uniformly- distributed data values (running from 75 to 125) that falls in the interval from 90 to 110 is (roughly) 0.40.

#Comment1. Count the number of data values in uniform_data that #are less than or equal to 90 (that is, all the data values that #fall in interval from 75 to 90); name this object a.

a <- length(which(uniform_data <= 90))

#Comment2. Examine the contents of a. Is it near 300,000? a ## [1] 300090 #Comment3. Count the number of data values in uniform_data that #are greater than or equal to 110 (that is, all the data values #that fall in the interval from 110 to 125); name this object b. b <- length(which(uniform_data >= 110)) #Comment4. Examine the contents of b. Is it near 300,000? b ## [1] 299374 #Comment5. Calculate the proportion of 1,000,000 data values that #fall in the interval from 90 to 110. Name that proportion c. c <- (1000000 - (a + b)) / 1000000 #Comment6. Examine the contents of c. Is it near 0.40? c ## [1] 0.400536 From the histogram, we see that a uniformly-distributed variable assumes the "shape" of a rectangle, and therefore the proportion of data values falling in any interval is directly proportional to the length of that interval. In this case, since the question concerns the proportion of data values in an interval of width 20 (= 110 - 90) for a distribution of width 50 (= 125 - 75), the proportion of data values falling in the interval from 90 to 110 is 20/50 or 0.40.

Please ensure that your password is at least 8 characters and contains each of the following:

• a special character: @$#!%*?&

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons

Margin Size

• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

10.E: Correlation and Regression (Exercises)

• Last updated
• Save as PDF
• Page ID 1115

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)

( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

\( \newcommand{\Span}{\mathrm{span}}\)

\( \newcommand{\id}{\mathrm{id}}\)

\( \newcommand{\kernel}{\mathrm{null}\,}\)

\( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\)

\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\)

\( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)

\( \newcommand{\vectorA}[1]{\vec{#1}}      % arrow\)

\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}}      % arrow\)

\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vectorC}[1]{\textbf{#1}} \)

\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)

\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)

\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)

These are homework exercises to accompany the Textmap created for "Introductory Statistics" by Shafer and Zhang.

10.1 Linear Relationships Between Variables

• Pick five distinct \(x\)-values, use the equation to compute the corresponding \(y\)-values, and plot the five points obtained.
• Give the value of the slope of the line; give the value of the \(y\)-intercept.
• The slope is positive.
• The \(y\)-intercept is positive.
• The slope is zero.
• The \(y\)-intercept is negative.
• The \(y\)-intercept is zero.
• The slope is negative.
• Plot the data in a scatter diagram.
• Based on the plot, explain whether the relationship between \(x\) and \(y\) appears to be deterministic or to involve randomness.
• Based on the plot, explain whether the relationship between \(x\) and \(y\) appears to be linear or not linear.

Applications

• Explain whether the relationship between the weight \(y\) and the amount \(x\) of gasoline is deterministic or contains an element of randomness.
• Predict the weight of gasoline on a tank truck that has just been loaded with \(6,750\) gallons of gasoline.
• Explain whether the relationship between the cost \(y\) of renting the scooter for a day and the distance \(x\) that the scooter is driven that day is deterministic or contains an element of randomness.
• A person intends to rent a scooter one day for a trip to an attraction \(17\) miles away. Assuming that the total distance the scooter is driven is \(34\) miles, predict the cost of the rental.
• Write down the linear equation that relates the labor cost \(y\) to the number of hours \(x\) that the repairman is on site.
• Calculate the labor cost for a service call that lasts \(2.5\) hours.
• Write down the linear equation that relates the cost \(y\) (in cents) of a call to its length \(x\).
• Calculate the cost of a call that lasts \(23\) minutes.

Large Data Set Exercises

Large Data Sets not available

• Large \(\text{Data Set 1}\) lists the SAT scores and GPAs of \(1,000\) students. Plot the scatter diagram with SAT score as the independent variable (\(x\)) and GPA as the dependent variable (\(y\)). Comment on the appearance and strength of any linear trend.
• Large \(\text{Data Set 12}\) lists the golf scores on one round of golf for \(75\) golfers first using their own original clubs, then using clubs of a new, experimental design (after two months of familiarization with the new clubs). Plot the scatter diagram with golf score using the original clubs as the independent variable (\(x\)) and golf score using the new clubs as the dependent variable (\(y\)). Comment on the appearance and strength of any linear trend.
• Large \(\text{Data Set 13}\) records the number of bidders and sales price of a particular type of antique grandfather clock at \(60\) auctions. Plot the scatter diagram with the number of bidders at the auction as the independent variable (\(x\)) and the sales price as the dependent variable (\(y\)). Comment on the appearance and strength of any linear trend.
• Answers vary.
• Slope \(m=0.5\); \(y\)-intercept \(b=2\) .
• Slope \(m=-2\); \(y\)-intercept \(b=4\) .
• \(y\) increases.
• Impossible to tell.
• \(y\) does not change.
• Scatter diagram needed.
• Involves randomness.
• Deterministic.
• Not linear.
• \(41,647.5\) pounds.
• \(y=50x+150\) .
• There appears to a hint of some positive correlation.
• There appears to be clear positive correlation.

10.2 The Linear Correlation Coefficient

With the exception of the exercises at the end of Section 10.3, the first Basic exercise in each of the following sections through Section 10.7 uses the data from the first exercise here, the second Basic exercise uses the data from the second exercise here, and so on, and similarly for the Application exercises. Save your computations done on these exercises so that you do not need to repeat them later.

• Draw the scatter plot.
• Based on the scatter plot, predict the sign of the linear correlation coefficient. Explain your answer.
• Compute the linear correlation coefficient and compare its sign to your answer to part (b).
• Compute the linear correlation coefficient for the sample data summarized by the following information: \[n=5\; \; \sum x=25\; \; \sum x^2=165\\ \sum y=24\; \; \sum y^2=134\; \; \sum xy=144\\ 1\leq x\leq 9\]
• Compute the linear correlation coefficient for the sample data summarized by the following information: \[n=5\; \; \sum x=31\; \; \sum x^2=253\\ \sum y=18\; \; \sum y^2=90\; \; \sum xy=148\\ 2\leq x\leq 12\]
• Compute the linear correlation coefficient for the sample data summarized by the following information: \[n=10\; \; \sum x=0\; \; \sum x^2=60\\ \sum y=24\; \; \sum y^2=234\; \; \sum xy=-87\\ -4\leq x\leq 4\]
• Compute the linear correlation coefficient for the sample data summarized by the following information: \[n=10\; \; \sum x=-3\; \; \sum x^2=263\\ \sum y=55\; \; \sum y^2=917\; \; \sum xy=-355\\ -10\leq x\leq 10\]
• The age \(x\) in months and vocabulary \(y\) were measured for six children, with the results shown in the table. \[\begin{array}{c|c c c c c c c} x &13 &14 &15 &16 &16 &18 \\ \hline y &8 &10 &15 &20 &27 &30\\ \end{array}\] Compute the linear correlation coefficient for these sample data and interpret its meaning in the context of the problem.
• The curb weight \(x\) in hundreds of pounds and braking distance \(y\) in feet, at \(50\) miles per hour on dry pavement, were measured for five vehicles, with the results shown in the table. \[\begin{array}{c|c c c c c c } x &25 &27.5 &32.5 &35 &45 \\ \hline y &105 &125 &140 &140 &150 \\ \end{array}\] Compute the linear correlation coefficient for these sample data and interpret its meaning in the context of the problem.
• The age \(x\) and resting heart rate \(y\) were measured for ten men, with the results shown in the table. \[\begin{array}{c|c c c c c c } x &20 &23 &30 &37 &35 \\ \hline y &72 &71 &73 &74 &74 \\ \end{array}\\ \begin{array}{c|c c c c c c } x &45 &51 &55 &60 &63 \\ \hline y &73 &72 &79 &75 &77 \\ \end{array}\\\] Compute the linear correlation coefficient for these sample data and interpret its meaning in the context of the problem.
• The wind speed \(x\) in miles per hour and wave height \(y\) in feet were measured under various conditions on an enclosed deep water sea, with the results shown in the table, \[\begin{array}{c|c c c c c c } x &0 &0 &2 &7 &7 \\ \hline y &2.0 &0.0 &0.3 &0.7 &3.3 \\ \end{array}\\ \begin{array}{c|c c c c c c } x &9 &13 &20 &22 &31 \\ \hline y &4.9 &4.9 &3.0 &6.9 &5.9 \\ \end{array}\\\] Compute the linear correlation coefficient for these sample data and interpret its meaning in the context of the problem.
• The advertising expenditure \(x\) and sales \(y\) in thousands of dollars for a small retail business in its first eight years in operation are shown in the table. \[\begin{array}{c|c c c c c } x &1.4 &1.6 &1.6 &2.0 \\ \hline y &180 &184 &190 &220 \\ \end{array}\\ \begin{array}{c|c c c c c c } x &2.0 &2.2 &2.4 &2.6 \\ \hline y &186 &215 &205 &240 \\ \end{array}\\\] Compute the linear correlation coefficient for these sample data and interpret its meaning in the context of the problem.
• The height \(x\) at age \(2\) and \(y\) at age \(20\), both in inches, for ten women are tabulated in the table. \[\begin{array}{c|c c c c c } x &31.3 &31.7 &32.5 &33.5 &34.4\\ \hline y &60.7 &61.0 &63.1 &64.2 &65.9 \\ \end{array}\\ \begin{array}{c|c c c c c } x &35.2 &35.8 &32.7 &33.6 &34.8 \\ \hline y &68.2 &67.6 &62.3 &64.9 &66.8 \\ \end{array}\\\] Compute the linear correlation coefficient for these sample data and interpret its meaning in the context of the problem.
• The course average \(x\) just before a final exam and the score \(y\) on the final exam were recorded for \(15\) randomly selected students in a large physics class, with the results shown in the table. \[\begin{array}{c|c c c c c } x &69.3 &87.7 &50.5 &51.9 &82.7\\ \hline y &56 &89 &55 &49 &61 \\ \end{array}\\ \begin{array}{c|c c c c c } x &70.5 &72.4 &91.7 &83.3 &86.5 \\ \hline y &66 &72 &83 &73 &82 \\ \end{array}\\ \begin{array}{c|c c c c c } x &79.3 &78.5 &75.7 &52.3 &62.2 \\ \hline y &92 &80 &64 &18 &76 \\ \end{array}\\\] Compute the linear correlation coefficient for these sample data and interpret its meaning in the context of the problem.
• The table shows the acres \(x\) of corn planted and acres \(y\) of corn harvested, in millions of acres, in a particular country in ten successive years. \[\begin{array}{c|c c c c c } x &75.7 &78.9 &78.6 &80.9 &81.8\\ \hline y &68.8 &69.3 &70.9 &73.6 &75.1 \\ \end{array}\\ \begin{array}{c|c c c c c } x &78.3 &93.5 &85.9 &86.4 &88.2 \\ \hline y &70.6 &86.5 &78.6 &79.5 &81.4 \\ \end{array}\\\] Compute the linear correlation coefficient for these sample data and interpret its meaning in the context of the problem.
• Fifty male subjects drank a measured amount \(x\) (in ounces) of a medication and the concentration \(y\) (in percent) in their blood of the active ingredient was measured \(30\) minutes later. The sample data are summarized by the following information. \[n=50\; \; \sum x=112.5\; \; \sum y=4.83\\ \sum xy=15.255\; \; 0\leq x\leq 4.5\\ \sum x^2=356.25\; \; \sum y^2=0.667\] Compute the linear correlation coefficient for these sample data and interpret its meaning in the context of the problem.
• In an effort to produce a formula for estimating the age of large free-standing oak trees non-invasively, the girth \(x\) (in inches) five feet off the ground of \(15\) such trees of known age \(y\) (in years) was measured. The sample data are summarized by the following information. \[n=15\; \; \sum x=3368\; \; \sum y=6496\\ \sum xy=1,933,219\; \; 74\leq x\leq 395\\ \sum x^2=917,780\; \; \sum y^2=4,260,666\] Compute the linear correlation coefficient for these sample data and interpret its meaning in the context of the problem.
• Construction standards specify the strength of concrete \(28\) days after it is poured. For \(30\) samples of various types of concrete the strength \(x\) after \(3\) days and the strength \(y\) after \(28\) days (both in hundreds of pounds per square inch) were measured. The sample data are summarized by the following information. \[n=30\; \; \sum x=501.6\; \; \sum y=1338.8\\ \sum xy=23,246.55\; \; 11\leq x\leq 22\\ \sum x^2=8724.74\; \; \sum y^2=61,980.14\] Compute the linear correlation coefficient for these sample data and interpret its meaning in the context of the problem.
• Power-generating facilities used forecasts of temperature to forecast energy demand. The average temperature \(x\) (degrees Fahrenheit) and the day’s energy demand \(y\) (million watt-hours) were recorded on \(40\) randomly selected winter days in the region served by a power company. The sample data are summarized by the following information. \[n=40\; \; \sum x=2000\; \; \sum y=2969\\ \sum xy=143,042\; \; 40\leq x\leq 60\\ \sum x^2=101,340\; \; \sum y^2=243,027\] Compute the linear correlation coefficient for these sample data and interpret its meaning in the context of the problem.

Additional Exercises

• the number \(x\) of pages in a book and the age \(y\) of the author
• the number \(x\) of pages in a book and the age \(y\) of the intended reader
• the weight \(x\) of an automobile and the fuel economy \(y\) in miles per gallon
• the weight \(x\) of an automobile and the reading \(y\) on its odometer
• the amount \(x\) of a sedative a person took an hour ago and the time \(y\) it takes him to respond to a stimulus
• the length \(x\) of time an emergency flare will burn and the length \(y\) of time the match used to light it burned
• the average length \(x\) of time that calls to a retail call center are on hold one day and the number \(y\) of calls received that day
• the length \(x\) of a regularly scheduled commercial flight between two cities and the headwind \(y\) encountered by the aircraft
• the value \(x\) of a house and the its size \(y\) in square feet
• the average temperature \(x\) on a winter day and the energy consumption \(y\) of the furnace
• Changing the units of measurement on two variables \(x\) and \(y\) should not change the linear correlation coefficient. Moreover, most change of units amount to simply multiplying one unit by the other (for example, \(1\) foot = \(12\) inches). Multiply each \(x\) value in the table in Exercise 1 by two and compute the linear correlation coefficient for the new data set. Compare the new value of \(r\) to the one for the original data.
• Refer to the previous exercise. Multiply each \(x\) value in the table in Exercise 2 by two, multiply each \(y\) value by three, and compute the linear correlation coefficient for the new data set. Compare the new value of \(r\) to the one for the original data.
• Reversing the roles of \(x\) and \(y\) in the data set of Exercise 1 produces the data set \[\begin{array}{c|c c c c c} x &2 &4 &6 &5 &9 \\ \hline y &0 &1 &3 &5 &8\\ \end{array}\] Compute the linear correlation coefficient of the new set of data and compare it to what you got in Exercise 1.
• In the context of the previous problem, look at the formula for \(r\) and see if you can tell why what you observed there must be true for every data set.
• Large \(\text{Data Set 1}\) lists the SAT scores and GPAs of \(1,000\) students. Compute the linear correlation coefficient \(r\). Compare its value to your comments on the appearance and strength of any linear trend in the scatter diagram that you constructed in the first large data set problem for Section 10.1.
• Large \(\text{Data Set 12}\) lists the golf scores on one round of golf for \(75\) golfers first using their own original clubs, then using clubs of a new, experimental design (after two months of familiarization with the new clubs). Compute the linear correlation coefficient \(r\). Compare its value to your comments on the appearance and strength of any linear trend in the scatter diagram that you constructed in the second large data set problem for Section 10.1.
• Large \(\text{Data Set 13}\) records the number of bidders and sales price of a particular type of antique grandfather clock at \(60\) auctions. Compute the linear correlation coefficient \(r\). Compare its value to your comments on the appearance and strength of any linear trend in the scatter diagram that you constructed in the third large data set problem for Section 10.1.
• \(r=0.921\)
• \(r=-0.794\)
• \(r=0.707\)
• \(r=0.4601\)
• \(r=0.9002\)

10.3 Modelling Linear Relationships with Randomness Present

• State the three assumptions that are the basis for the Simple Linear Regression Model.
• The Simple Linear Regression Model is summarized by the equation \[y=\beta _1x+\beta _0+\varepsilon\] Identify the deterministic part and the random part.
• Is the number \(\beta _1\) in the equation \(y=\beta _1x+\beta _0\) a statistic or a population parameter? Explain.
• Is the number \(\sigma\) in the Simple Linear Regression Model a statistic or a population parameter? Explain.
• Describe what to look for in a scatter diagram in order to check that the assumptions of the Simple Linear Regression Model are true.
• True or false: the assumptions of the Simple Linear Regression Model must hold exactly in order for the procedures and analysis developed in this chapter to be useful.
• The mean of \(y\) is linearly related to \(x\).
• For each given \(x\), \(y\) is a normal random variable with mean \(\beta _1x+\beta _0\) and a standard deviation \(\sigma\).
• All the observations of \(y\) in the sample are independent.
• \(\beta _1\) is a population parameter.
• A linear trend.

10.4 The Least Squares Regression Line

For the Basic and Application exercises in this section use the computations that were done for the exercises with the same number in Section 10.2.

• Compute the least squares regression line for the data in Exercise 1 of Section 10.2.
• Compute the least squares regression line for the data in Exercise 2 of Section 10.2.
• Compute the least squares regression line for the data in Exercise 3 of Section 10.2.
• Compute the least squares regression line for the data in Exercise 4 of Section 10.2.
• Compute the least squares regression line.
• Compute the sum of the squared errors \(\text{SSE}\) using the definition \(\sum (y-\hat{y})^2\).
• Compute the sum of the squared errors \(\text{SSE}\) using the formula \(SSE=SS_{yy}-\widehat{\beta _1}SS_{xy}\).
• Compute the least squares regression line for the data in Exercise 7 of Section 10.2.
• Compute the least squares regression line for the data in Exercise 8 of Section 10.2.
• Can you compute the sum of the squared errors \(\text{SSE}\) using the definition \(\sum (y-\hat{y})^2\)? Explain.
• On average, how many new words does a child from \(13\) to \(18\) months old learn each month? Explain.
• Estimate the average vocabulary of all \(16\)-month-old children.
• On average, how many additional feet are added to the braking distance for each additional \(100\) pounds of weight? Explain.
• Estimate the average braking distance of all cars weighing \(3,000\) pounds.
• Estimate the average resting heart rate of all \(40\)-year-old men.
• Estimate the average resting heart rate of all newborn baby boys. Comment on the validity of the estimate.
• Estimate the average wave height when the wind is blowing at \(10\) miles per hour.
• Estimate the average wave height when there is no wind blowing. Comment on the validity of the estimate.
• On average, for each additional thousand dollars spent on advertising, how does revenue change? Explain.
• Estimate the revenue if \(\$2,500\) is spent on advertising next year.
• On average, for each additional inch of height of two-year-old girl, what is the change in the adult height? Explain.
• Predict the adult height of a two-year-old girl who is \(33\) inches tall.
• Compute \(\text{SSE}\) using the formula \(SSE=SS_{yy}-\widehat{\beta _1}SS_{xy}\).
• Estimate the average final exam score of all students whose course average just before the exam is \(85\).
• Estimate the number of acres that would be harvested if \(90\) million acres of corn were planted.
• Interpret the value of the slope of the least squares regression line in the context of the problem.
• Estimate the average concentration of the active ingredient in the blood in men after consuming \(1\) ounce of the medication.
• Estimate the age of an oak tree whose girth five feet off the ground is \(92\) inches.
• The \(28\)-day strength of concrete used on a certain job must be at least \(3,200\) psi. If the \(3\)-day strength is \(1,300\) psi, would we anticipate that the concrete will be sufficiently strong on the \(28^{th}\) day? Explain fully.
• If the power facility is called upon to provide more than \(95\) million watt-hours tomorrow then energy will have to be purchased from elsewhere at a premium. The forecast is for an average temperature of \(42\) degrees. Should the company plan on purchasing power at a premium?
• Verify that no matter what the data are, the least squares regression line always passes through the point with coordinates \((\bar{x},\bar{y})\). Hint: Find the predicted value of \(y\) when \(x=\bar{x}\).
• Reverse the roles of x and y and compute the least squares regression line for the new data set \[\begin{array}{c|c c c c c c} x &2 &4 &6 &5 &9 \\ \hline y &0 &1 &3 &5 &8\\ \end{array}\]
• Interchanging x and y corresponds geometrically to reflecting the scatter plot in a 45-degree line. Reflecting the regression line for the original data the same way gives a line with the equation \(\bar{y}=1.346x-3.600\). Is this the equation that you got in part (a)? Can you figure out why not? Hint: Think about how x and y are treated differently geometrically in the computation of the goodness of fit.
• Compute \(\text{SSE}\) for each line and see if they fit the same, or if one fits the data better than the other.
• Compute the least squares regression line with SAT score as the independent variable (\(x\)) and GPA as the dependent variable (\(y\)).
• Interpret the meaning of the slope \(\widehat{\beta _1}\) of regression line in the context of problem.
• Compute \(\text{SSE}\) the measure of the goodness of fit of the regression line to the sample data.
• Estimate the GPA of a student whose SAT score is \(1350\).
• Compute the least squares regression line with scores using the original clubs as the independent variable (\(x\)) and scores using the new clubs as the dependent variable (\(y\)).
• Estimate the score with the new clubs of a golfer whose score with the old clubs is \(73\).
• Compute the least squares regression line with the number of bidders present at the auction as the independent variable (\(x\)) and sales price as the dependent variable (\(y\)).
• Estimate the sales price of a clock at an auction at which the number of bidders is seven.
• \(\hat{y}=0.743x+2.675\)
• \(\hat{y}=-0.610x+4.082\)
• \(\hat{y}=0.625x+1.25,\; SSE=5\)
• \(\hat{y}=0.6x+1.8\)
• \(\hat{y}=-1.45x+2.4,\; SSE=50.25\) (cannot use the definition to compute)
• \(\hat{y}=4.848x-56\)
• \(\hat{y}=0.114x+69.222\)
• \(69.2\), invalid extrapolation
• \(\hat{y}=42.024x+119.502\)
• increases by \(\$42,024\)
• \(\$224,562\)
• \(\hat{y}=1.045x-8.527\)
• \(2151.93367\)
• \(\hat{y}=0.043x+0.001\)
• For each additional ounce of medication consumed blood concentration of the active ingredient increases by \(0.043\%\)
• \(0.044\%\)
• \(\hat{y}=2.550x+1.993\)
• Predicted \(28\)-day strength is \(3,514\) psi; sufficiently strong
• \(\hat{y}=0.0016x+0.022\)
• On average, every \(100\) point increase in SAT score adds \(0.16\) point to the GPA.
• \(SSE=432.10\)
• \(\hat{y}=2.182\)
• \(\hat{y}=116.62x+6955.1\)
• On average, every \(1\) additional bidder at an auction raises the price by \(116.62\) dollars.
• \(SSE=1850314.08\)
• \(\hat{y}=7771.44\)

10.5 Statistical Inferences About β1

For the Basic and Application exercises in this section use the computations that were done for the exercises with the same number in Section 10.2 and Section 10.4.

• Construct the \(95\%\) confidence interval for the slope \(\beta _1\) of the population regression line based on the sample data set of Exercise 1 of Section 10.2.
• Construct the \(90\%\) confidence interval for the slope \(\beta _1\) of the population regression line based on the sample data set of Exercise 2 of Section 10.2.
• Construct the \(90\%\) confidence interval for the slope \(\beta _1\) of the population regression line based on the sample data set of Exercise 3 of Section 10.2.
• Construct the \(99\%\) confidence interval for the slope \(\beta _1\) of the population regression line based on the sample data set of Exercise 4 of Section 10.2.
• For the data in Exercise 5 of Section 10.2 test, at the \(10\%\) level of significance, whether \(x\) is useful for predicting \(y\) (that is, whether \(\beta _1\neq 0\)).
• For the data in Exercise 6 of Section 10.2 test, at the \(5\%\) level of significance, whether \(x\) is useful for predicting \(y\) (that is, whether \(\beta _1\neq 0\)).
• Construct the \(90\%\) confidence interval for the slope \(\beta _1\) of the population regression line based on the sample data set of Exercise 7 of Section 10.2.
• Construct the \(95\%\) confidence interval for the slope \(\beta _1\) of the population regression line based on the sample data set of Exercise 8 of Section 10.2.
• For the data in Exercise 9 of Section 10.2 test, at the \(1\%\) level of significance, whether \(x\) is useful for predicting \(y\) (that is, whether \(\beta _1\neq 0\)).
• For the data in Exercise 10 of Section 10.2 test, at the \(1\%\) level of significance, whether \(x\) is useful for predicting \(y\) (that is, whether \(\beta _1\neq 0\)).
• For the data in Exercise 11 of Section 10.2 construct a \(90\%\) confidence interval for the mean number of new words acquired per month by children between \(13\) and \(18\) months of age.
• For the data in Exercise 12 of Section 10.2 construct a \(90\%\) confidence interval for the mean increased braking distance for each additional \(100\) pounds of vehicle weight.
• For the data in Exercise 13 of Section 10.2 test, at the \(10\%\) level of significance, whether age is useful for predicting resting heart rate.
• For the data in Exercise 14 of Section 10.2 test, at the \(10\%\) level of significance, whether wind speed is useful for predicting wave height.
• Construct the \(95\%\) confidence interval for the mean increase in revenue per additional thousand dollars spent on advertising.
• An advertising agency tells the business owner that for every additional thousand dollars spent on advertising, revenue will increase by over \(\$25,000\). Test this claim (which is the alternative hypothesis) at the \(5\%\) level of significance.
• Perform the test of part (b) at the \(10\%\) level of significance.
• Based on the results in (b) and (c), how believable is the ad agency’s claim? (This is a subjective judgement.)
• Construct the \(90\%\) confidence interval for the mean increase in height per additional inch of length at age two.
• It is claimed that for girls each additional inch of length at age two means more than an additional inch of height at maturity. Test this claim (which is the alternative hypothesis) at the \(10\%\) level of significance.
• For the data in Exercise 17 of Section 10.2 test, at the \(10\%\) level of significance, whether course average before the final exam is useful for predicting the final exam grade.
• For the situation described in Exercise 18 of Section 10.2, an agronomist claims that each additional million acres planted results in more than \(750,000\) additional acres harvested. Test this claim at the \(1\%\) level of significance.
• For the data in Exercise 19 of Section 10.2 test, at the \(1/10\)th of \(1\%\) level of significance, whether, ignoring all other facts such as age and body mass, the amount of the medication consumed is a useful predictor of blood concentration of the active ingredient.
• For the data in Exercise 20 of Section 10.2 test, at the \(1\%\) level of significance, whether for each additional inch of girth the age of the tree increases by at least two and one-half years.
• Construct the \(95\%\) confidence interval for the mean increase in strength at \(28\) days for each additional hundred psi increase in strength at \(3\) days.
• Test, at the \(1/10\)th of \(1\%\) level of significance, whether the \(3\)-day strength is useful for predicting \(28\)-day strength.
• Construct the \(99\%\) confidence interval for the mean decrease in energy demand for each one-degree drop in temperature.
• An engineer with the power company believes that for each one-degree increase in temperature, daily energy demand will decrease by more than \(3.6\) million watt-hours. Test this claim at the \(1\%\) level of significance.
• Compute the \(90\%\) confidence interval for the slope \(\beta _1\) of the population regression line with SAT score as the independent variable (\(x\)) and GPA as the dependent variable (\(y\)).
• Test, at the \(10\%\) level of significance, the hypothesis that the slope of the population regression line is greater than \(0.001\), against the null hypothesis that it is exactly \(0.001\).
• Compute the \(95\%\) confidence interval for the slope \(\beta _1\) of the population regression line with scores using the original clubs as the independent variable (\(x\)) and scores using the new clubs as the dependent variable (\(y\)).
• Test, at the \(10\%\) level of significance, the hypothesis that the slope of the population regression line is different from \(1\), against the null hypothesis that it is exactly \(1\).
• Compute the \(95\%\) confidence interval for the slope \(\beta _1\) of the population regression line with the number of bidders present at the auction as the independent variable(\(x\)) and sales price as the dependent variable (\(y\)).
• Test, at the \(10\%\) level of significance, the hypothesis that the average sales price increases by more than \(\$90\) for each additional bidder at an auction, against the default that it increases by exactly \(\$90\).
• \(0.743\pm 0.578\)
• \(-0.610\pm 0.633\)
• \(T=1.732,\; \pm t_{0.05}=\pm 2.353\), do not reject \(H_0\)
• \(0.6\pm 0.451\)
• \(T=-4.481,\; \pm t_{0.005}=\pm 3.355\), reject \(H_0\)
• \(4.8\pm 1.7\) words
• \(T=2.843,\; \pm t_{0.05}=\pm 1.860\), reject \(H_0\)
• \(42.024\pm 28.011\) thousand dollars
• \(T=1.487,\; \pm t_{0.05}=\pm 1.943\), do not reject \(H_0\)
• \(t_{0.10}=1.440\), reject \(H_0\)
• \(T=4.096,\; \pm t_{0.05}=\pm 1.771\), reject \(H_0\)
• \(T=25.524,\; \pm t_{0.0005}=\pm 3.505\), reject \(H_0\)
• \(2.550\pm 0.127\) hundred psi
• \(T=41.072,\; \pm t_{0.005}=\pm 3.674\), reject \(H_0\)
• \((0.0014,0.0018)\)
• \(H_0:\beta _1=0.001\; vs\; H_a:\beta _1>0.001\). Test Statistic: \(Z=6.1625\). Rejection Region: \([1.28,+\infty )\). Decision: Reject \(H_0\)
• \((101.789,131.4435)\)
• \(H_0:\beta _1=90\; vs\; H_a:\beta _1>90\). Test Statistic: \(T=3.5938,\; d.f.=58\). Rejection Region: \([1.296,+\infty )\). Decision: Reject \(H_0\)

10.6 The Coefficient of Determination

For the Basic and Application exercises in this section use the computations that were done for the exercises with the same number in Section 10.2, Section 10.4, and Section 10.5.

• For the sample data set of Exercise 1 of Section 10.2 find the coefficient of determination using the formula \(r^2=\widehat{\beta _1}SS_{xy}/SS_{yy}\). Confirm your answer by squaring \(r\) as computed in that exercise.
• For the sample data set of Exercise 2 of Section 10.2" find the coefficient of determination using the formula \(r^2=\widehat{\beta _1}SS_{xy}/SS_{yy}\). Confirm your answer by squaring \(r\) as computed in that exercise.
• For the sample data set of Exercise 3 of Section 10.2 find the coefficient of determination using the formula \(r^2=\widehat{\beta _1}SS_{xy}/SS_{yy}\). Confirm your answer by squaring \(r\) as computed in that exercise.
• For the sample data set of Exercise 4 of Section 10.2 find the coefficient of determination using the formula \(r^2=\widehat{\beta _1}SS_{xy}/SS_{yy}\). Confirm your answer by squaring \(r\) as computed in that exercise.
• For the sample data set of Exercise 5 of Section 10.2 find the coefficient of determination using the formula \(r^2=\widehat{\beta _1}SS_{xy}/SS_{yy}\). Confirm your answer by squaring \(r\) as computed in that exercise.
• For the sample data set of Exercise 6 of Section 10.2 find the coefficient of determination using the formula \(r^2=\widehat{\beta _1}SS_{xy}/SS_{yy}\). Confirm your answer by squaring \(r\) as computed in that exercise.
• For the sample data set of Exercise 7 of Section 10.2 find the coefficient of determination using the formula \(r^2=(SS_{yy}-SSE)/SS_{yy}\). Confirm your answer by squaring \(r\) as computed in that exercise.
• For the data in Exercise 11 of Section 10.2 compute the coefficient of determination and interpret its value in the context of age and vocabulary.
• For the data in Exercise 12 of Section 10.2" compute the coefficient of determination and interpret its value in the context of vehicle weight and braking distance.
• For the data in Exercise 13 of Section 10.2 compute the coefficient of determination and interpret its value in the context of age and resting heart rate. In the age range of the data, does age seem to be a very important factor with regard to heart rate?
• For the data in Exercise 14 of Section 10.2 compute the coefficient of determination and interpret its value in the context of wind speed and wave height. Does wind speed seem to be a very important factor with regard to wave height?
• For the data in Exercise 15 of Section 10.2 find the proportion of the variability in revenue that is explained by level of advertising.
• For the data in Exercise 16 of Section 10.2 find the proportion of the variability in adult height that is explained by the variation in length at age two.
• For the data in Exercise 17 of Section 10.2 compute the coefficient of determination and interpret its value in the context of course average before the final exam and score on the final exam.
• For the data in Exercise 18 of Section 10.2 compute the coefficient of determination and interpret its value in the context of acres planted and acres harvested.
• For the data in Exercise 19 of Section 10.2 compute the coefficient of determination and interpret its value in the context of the amount of the medication consumed and blood concentration of the active ingredient.
• For the data in Exercise 20 of Section 10.2 compute the coefficient of determination and interpret its value in the context of tree size and age.
• For the data in Exercise 21 of Section 10.2 find the proportion of the variability in \(28\)-day strength of concrete that is accounted for by variation in \(3\)-day strength.
• For the data in Exercise 22 of Section 10.2 find the proportion of the variability in energy demand that is accounted for by variation in average temperature.
• Large \(\text{Data Set 1}\) lists the SAT scores and GPAs of \(1,000\) students. Compute the coefficient of determination and interpret its value in the context of SAT scores and GPAs.
• Large \(\text{Data Set 12}\) lists the golf scores on one round of golf for \(75\) golfers first using their own original clubs, then using clubs of a new, experimental design (after two months of familiarization with the new clubs). Compute the coefficient of determination and interpret its value in the context of golf scores with the two kinds of golf clubs.
• Large \(\text{Data Set 13}\) records the number of bidders and sales price of a particular type of antique grandfather clock at \(60\) auctions. Compute the coefficient of determination and interpret its value in the context of the number of bidders at an auction and the price of this type of antique grandfather clock.
• \(0.898\); about \(90\%\) of the variability in vocabulary is explained by age
• \(0.503\); about \(50\%\) of the variability in heart rate is explained by age. Age is a significant but not dominant factor in explaining heart rate.
• The proportion is \(r^2=0.692\)
• \(0.563\); about \(56\%\) of the variability in final exam scores is explained by course average before the final exam
• \(0.931\); about \(93\%\) of the variability in the blood concentration of the active ingredient is explained by the amount of the medication consumed
• The proportion is \(r^2=0.984\)
• \(r^2=21.17\%\)
• \(r^2=81.04\%\)

10.7 Estimation and Prediction

For the Basic and Application exercises in this section use the computations that were done for the exercises with the same number in previous sections.

• Give a point estimate for the mean value of \(y\) in the sub-population determined by the condition \(x = 4\).
• Construct the \(90\%\) confidence interval for that mean value.
• Give a point estimate for the mean value of \(y\) in the sub-population determined by the condition \(x = 7\).
• Construct the \(95\%\) confidence interval for that mean value.
• Give a point estimate for the mean value of \(y\) in the sub-population determined by the condition \(x = 2\).
• Construct the \(80\%\) confidence interval for that mean value.
• Give a point estimate for the mean value of \(y\) in the sub-population determined by the condition \(x = 1\).
• Give a point estimate for the mean value of \(y\) in the sub-population determined by the condition \(x = 5\).
• Give a point estimate for the mean value of \(y\) in the sub-population determined by the condition \(x = 6\).
• Construct the \(99\%\) confidence interval for that mean value.
• Is it valid to make the same estimates for \(x = 12\)? Explain.
• Give a point estimate for the mean value of \(y\) in the sub-population determined by the condition \(x = 12\).
• Is it valid to make the same estimates for \(x = 0\)? Explain.
• Give a point estimate for the mean value of \(y\) in the sub-population determined by the condition \(x = 0\).
• Is it valid to make the same estimates for \(x = -1\)? Explain.
• Give a point estimate for the mean value of \(y\) in the sub-population determined by the condition \(x = 8\).
• Give a point estimate for the average number of words in the vocabulary of \(18\)-month-old children.
• Give a point estimate for the average braking distance of automobiles that weigh \(3,250\) pounds.
• Is it valid to make the same estimates for \(5,000\)-pound automobiles? Explain.
• Give a point estimate for the resting heart rate of a man who is \(35\) years old.
• One of the men in the sample is \(35\) years old, but his resting heart rate is not what you computed in part (a). Explain why this is not a contradiction.
• Construct the \(90\%\) confidence interval for the mean resting heart rate of all \(35\)-year-old men.
• Give a point estimate for the wave height when the wind speed is \(13\) miles per hour.
• One of the wind speeds in the sample is \(13\) miles per hour, but the height of waves that day is not what you computed in part (a). Explain why this is not a contradiction.
• Construct the \(95\%\) confidence interval for the mean wave height on days when the wind speed is \(13\) miles per hour.
• The business owner intends to spend \(\$2,500\) on advertising next year. Give an estimate of next year’s revenue based on this fact.
• Construct the \(90\%\) prediction interval for next year’s revenue, based on the intent to spend \(\$2,500\) on advertising.
• A two-year-old girl is \(32.3\) inches long. Predict her adult height.
• Construct the \(95\%\) prediction interval for the girl’s adult height.
• Lodovico has a \(78.6\) average in his physics class just before the final. Give a point estimate of what his final exam grade will be.
• Explain whether an interval estimate for this problem is a confidence interval or a prediction interval.
• Based on your answer to (b), construct an interval estimate for Lodovico’s final exam grade at the \(90\%\) level of confidence.
• This year \(86.2\) million acres of corn were planted. Give a point estimate of the number of acres that will be harvested this year.
• Based on your answer to (b), construct an interval estimate for the number of acres that will be harvested this year, at the \(99\%\) level of confidence.
• Give a point estimate for the blood concentration of the active ingredient of this medication in a man who has consumed \(1.5\) ounces of the medication just recently.
• Gratiano just consumed \(1.5\) ounces of this medication \(30\) minutes ago. Construct a \(95\%\) prediction interval for the concentration of the active ingredient in his blood right now.
• You measure the girth of a free-standing oak tree five feet off the ground and obtain the value \(127\) inches. How old do you estimate the tree to be?
• Construct a \(90\%\) prediction interval for the age of this tree.
• A test cylinder of concrete three days old fails at \(1,750\) psi. Predict what the \(28\)-day strength of the concrete will be.
• Construct a \(99\%\) prediction interval for the \(28\)-day strength of this concrete.
• Based on your answer to (b), what would be the minimum \(28\)-day strength you could expect this concrete to exhibit?
• Tomorrow’s average temperature is forecast to be \(53\) degrees. Estimate the energy demand tomorrow.
• Construct a \(99\%\) prediction interval for the energy demand tomorrow.
• Based on your answer to (b), what would be the minimum demand you could expect?
• Give a point estimate of the mean GPA of all students who score \(1350\) on the SAT.
• Construct a \(90\%\) confidence interval for the mean GPA of all students who score \(1350\) on the SAT.
• Thurio averages \(72\) strokes per round with his own clubs. Give a point estimate for his score on one round if he switches to the new clubs.
• Based on your answer to (b), construct an interval estimate for Thurio’s score on one round if he switches to the new clubs, at \(90\%\) confidence.
• There are seven likely bidders at the Verona auction today. Give a point estimate for the price of such a clock at today’s auction.
• Based on your answer to (b), construct an interval estimate for the likely sale price of such a clock at today’s sale, at \(95\%\) confidence.
• \(5.647\pm 1.253\)
• \(-0.188\pm 3.041\)
• \(1.875\pm 1.423\)
• \(5.4\pm 3.355\)
• invalid (extrapolation)
• 2.4 ± 1.474 2.4 ± 1.474 \(2.4\pm 1.474\)
• valid (\(-1\) is in the range of the \(x\)-values in the data set)
• \(31.3\) words
• \(31.3\pm 7.1\) words
• not valid, since two years is \(24\) months, hence this is extrapolation
• \(73.2\) beats/min
• The man’s heart rate is not the predicted average for all men his age.
• \(73.2\pm 1.2\) beats/min
• \(\$224,562 \pm \$28,699\)
• Prediction (one person, not an average for all who have average \(78.6\) before the final exam)
• \(74\pm 24\)
• \(0.066\%\)
• \(0.066\pm 0.034\%\)
• \(4,656\) psi
• 4,656 ± 321 \(4,656\pm 321\) psi
• \(4,656-321=4,335\) psi
• \((2.1421,2.2316)\)
• \(7771.39\)
• A prediction interval.
• \((7410.41,8132.38)\)

Solver Title

Generating PDF...

• Pre Algebra Order of Operations Factors & Primes Fractions Long Arithmetic Decimals Exponents & Radicals Ratios & Proportions Percent Modulo Number Line Expanded Form Mean, Median & Mode
• Algebra Equations Inequalities System of Equations System of Inequalities Basic Operations Algebraic Properties Partial Fractions Polynomials Rational Expressions Sequences Power Sums Interval Notation Pi (Product) Notation Induction Logical Sets Word Problems
• Pre Calculus Equations Inequalities Scientific Calculator Scientific Notation Arithmetics Complex Numbers Polar/Cartesian Simultaneous Equations System of Inequalities Polynomials Rationales Functions Arithmetic & Comp. Coordinate Geometry Plane Geometry Solid Geometry Conic Sections Trigonometry
• Calculus Derivatives Derivative Applications Limits Integrals Integral Applications Integral Approximation Series ODE Multivariable Calculus Laplace Transform Taylor/Maclaurin Series Fourier Series Fourier Transform
• Functions Line Equations Functions Arithmetic & Comp. Conic Sections Transformation
• Linear Algebra Matrices Vectors
• Trigonometry Identities Proving Identities Trig Equations Trig Inequalities Evaluate Functions Simplify
• Statistics Mean Geometric Mean Quadratic Mean Average Median Mode Order Minimum Maximum Probability Mid-Range Range Standard Deviation Variance Lower Quartile Upper Quartile Interquartile Range Midhinge Standard Normal Distribution
• Physics Mechanics
• Chemistry Chemical Reactions Chemical Properties
• Finance Simple Interest Compound Interest Present Value Future Value
• Economics Point of Diminishing Return
• Conversions Roman Numerals Radical to Exponent Exponent to Radical To Fraction To Decimal To Mixed Number To Improper Fraction Radians to Degrees Degrees to Radians Hexadecimal Scientific Notation Distance Weight Time Volume
• Pre Algebra
• Pre Calculus
• Linear Algebra
• Trigonometry
• Geometric Mean
• Quadratic Mean
• Probability
• Standard Deviation
• Lower Quartile
• Upper Quartile
• Interquartile Range
• Standard Normal Distribution
• Conversions

Most Used Actions

Number line.

• arithmetic\:mean\:1,\:2,\:3,\:4,\:5,\:6
• geometric\:mean\:\left\{0.42,\:0.52,\:0.58,\:0.62\right\}
• quadratic\:mean\:-4,\:5,\:6,\:9
• median\:\:\left\{1,\:7,\:-3,\:4,\:9\right\}
• mode\:\left\{90,\:94,\:53,\:68,\:79,\:94,\:87,\:90,\:70,\:69,\:65,\:89,\:85\right\}
• minimum\:-4,\:5,\:6,\:9
• maximum\:\frac{31}{100},\:\frac{23}{105},\:\frac{31}{205},\:\frac{54}{205}
• mid\:range\:1,\:2,\:3,\:4,\:5,\:6
• range\:\:\left\{1,\:7,\:-3,\:4,\:9\right\}
• standard\:deviation\:\:\left\{1,\:7,\:-3,\:4,\:9\right\}
• variance\:1,\:2,\:3,\:4,\:5,\:6
• lower\:quartile\:-4,\:5,\:6,\:9
• upper\:quartile\:\left\{0.42,\:0.52,\:0.58,\:0.62\right\}
• interquartile\:range\:1,\:2,\:3,\:4,\:5,\:6
• midhinge\:\left\{90,\:94,\:53,\:68,\:79,\:84,\:87,\:72,\:70,\:69,\:65,\:89,\:85\right\}
• What is the best calculator for statistics?
• Symbolab offers an online calculator specifically for statistics that can perform a wide range of calculations, including standard deviation, variance, range and normal distribution. It also provides detailed step-by-step solutions.
• What is statistics?
• Statistics is the branch of mathematics that deals with the collection, analysis, interpretation, presentation, and organization of data. There are two main branches of statistics: descriptive statistics, and inferential statistics.
• What is descriptive statistics?
• Descriptive statistics is a branch of statistics that deals with summarizing, organizing and describing data. Descriptive statistics uses measures such as central tendency (mean, median, and mode) and measures of variability (range, standard deviation, variance) to give an overview of the data.
• What is inferential statistics?
• Inferential statistics is a branch of statistics that deals with making predictions and inferences about a population based on a sample of data. Inferential statistics uses probability theory and statistical models to make predictions and inferences about a population.
• What is the difference between statistics and probability?
• Statistics is the branch of mathematics dealing with the collection, analysis, interpretation, presentation, and organization of data, while probability is the branch of mathematics dealing with the likelihood of occurrence of different events.

statistics-calculator

• Lies, Damned Lies, and Statistics Statistics is about analyzing data, for instance the mean is commonly used to measure the “central tendency” of...

Please add a message.

Message received. Thanks for the feedback.

Free Mathematics Tutorials

Linear Regression Problems with Solutions

Linear regression and modelling problems are presented along with their solutions at the bottom of the page. Also a linear regression calculator and grapher may be used to check answers and create more opportunities for practice.

Solutions to the Above Problems

More references and links.

• Linear Regression Calculator and Grapher .
• Linear Least Squares Fitting.
• elementary statistics and probabilities .

Popular Pages

• Normal Distribution Problems with Answers
• Free Mathematics Tutorials, Problems and Worksheets (with applets)
• Elementary Statistics and Probability Tutorials and Problems
• Free Algebra Questions and Problems with Answers
• Statistics and Probability Problems with Answers - sample 2

Stay In Touch

• Privacy Policy

This is an active research project

We're here to help, feedback is appreciated.

Limitations

Upload a screenshot and solve any math, physics, or accounting problem instantly with MathGPT!

Drag & drop an image file here, or click to select an image.