linear equations in one variable and problem solving

• Math Article
• Linear Equation In One Variable

Linear Equation in One Variable

The linear equations in one variable  is an equation which is expressed in the form of ax+b = 0, where a and b are two integers, and x is a variable and has only one solution. For example, 2x+3=8 is a linear equation having a single variable in it. Therefore, this equation has only one solution, which is x = 5/2. Whereas if we speak about linear equation in two variables, it has two solutions.

The concept of linear equation in one variable has been covered in this lesson, including its definition, solutions, examples, word problems and worksheet questions. This is an important topic for Class 6, 7 and 8 students. The concepts covered in this lesson are mentioned below in the table of contents. So, what is one variable equation?

Table of Content:

Linear Equation in One Variable Definition

A linear equation in one variable is an equation which has a maximum of one variable of order 1. It is of the form ax + b = 0 , where x is the variable.

This equation has only one solution. A few examples are:

Standard Form of Linear Equations in One Variable

The standard form of linear equations in one variable is represented as:

• ‘a’ and ‘b’ are real numbers.
• Both ‘a’ and ‘b’ are not equal to zero.

Thus, the formula of linear equation in one variable is ax + b = 0.

Solving Linear Equations in One Variable

For solving an equation having only one variable, the following steps are followed

• Step 1 : Using LCM, clear the fractions if any.
• Step 2: Simplify both sides of the equation.
• Step 3: Isolate the variable.
• Step 4: Verify your answer.

Example of Solution of Linear Equation in One Variable

Let us understand the concept with the help of an example.

For solving equations with variables on both sides, the following steps are followed:

Consider the equation: 5x – 9 = -3x + 19

Step 1: Transpose all the variables on one side of the equation. By transpose, we mean to shift the variables from one side of the equation to the other side of the equation. In the method of transposition, the operation on the operand gets reversed.

In the equation 5x – 9 = -3x + 19, we transpose -3x from the right-hand side to the left-hand side of the equality, the operation gets reversed upon transposition and the equation becomes:

5x – 9 +3x = 19

⇒ 8x -9 = 19

Step 2: Similarly transpose all the constant terms on the other side of the equation as below:

⇒ 8x = 19 + 9

Step 3: Divide the equation with 8 on both sides of the equality.

8x/8 = 28/8

If we substitute x = 28/8 in the equation 5x – 9 = -3x + 19, we will get 9 = 9, thereby satisfying the equality and giving us the required solution.

Related Topics:

• Application of linear equations
• Linear Equations Formula
• Graphing Of Linear Equations
• Linear Equations In Two Variables Class 9
• Important Questions Class 8 Maths Chapter 2 Linear Equations One Variable
• Linear Equations One Variable Worksheet

Linear Equation in One Variable Examples

Example 1 : Solve for x, 2x – 4 = 0

Add 4 both sides

2x – 4 + 4 = 0 + 4

Divide each side by 2, we get

x = 4/2 = 2

So, x = 2 is the answer.

Example 2: Solve 12m – 10 = 6

12m – 10 = 6

Add 10 both sides

12m – 10 + 10 = 6 + 10

Divide each side by 12, we get

12m/12 = 16/12

m = 16/12 = 4/3

Answer: m = 4/3

Linear Equations in One Variable Word Problems

Problem: The length of the legs of an isosceles triangle is 4 meters more than its base. If the Perimeter of the triangle is 44 meters, find the lengths of the sides of the triangle.

Let us assume the base measures ‘x’ meter. Hence, each of the legs measure y = (x + 4) meters.

The Perimeter of a triangle is the sum of the three sides.

The equations are formed and solved as follows:

x + 2(x + 4) = 44

x + 2x + 8 = 44

3x + 8 = 44

3x = 44 – 8 = 36

The length of the base is solved as 12 meters. Hence, each of the two legs measure 16 meters.

Linear Equations in One Variable Word Questions (Worksheet)

A few practice questions are given below.

• Question 1: Solve ( 10x – 7) = 21
• Question 2: Find the multiples, if the sum of two consecutive multiples of 6 is 68.
• Question 3: Verify that if x = -3, is a solution of the linear equation 10x + 7 = 13 – 5x.

Frequently Asked Questions

How many solutions does a linear equation in one variable have.

Every linear equation in one variable has a one and unique solution. If the equation has two or more variables then it becomes a linear equation in two variables or linear equations in three variables and so on and the number of solutions varies as per the count of variables an equation contains.

What is the formula of linear equation in one variable?

The formula or the standard form of an equation having only 1 variable is given as ax + b = 0. In this, there is only 1 variable, i.e. x.

How to easily solve any equation having one variable?

First, put the variable on the left-hand side and the numerical values on the right-hand side. Change the operators while changing sides of the terms and then solve for the variable.

Put your understanding of this concept to test by answering a few MCQs. Click ‘Start Quiz’ to begin!

Select the correct answer and click on the “Finish” button Check your score and answers at the end of the quiz

Visit BYJU’S for all Maths related queries and study materials

Your result is as below

Request OTP on Voice Call

Leave a Comment Cancel reply

Your Mobile number and Email id will not be published. Required fields are marked *

Post My Comment

Hi my name is abhay pratap singh

Please give me lenear eqation in two variable question

Please check: https://byjus.com/maths/linear-equations-in-two-variables/

Register with BYJU'S & Download Free PDFs

Register with byju's & watch live videos.

5.2 Linear Equations in One Variable with Applications

Learning objectives.

After completing this section, you should be able to:

• Solve linear equations in one variable using properties of equations.
• Construct a linear equation to solve applications.
• Determine equations with no solution or infinitely many solutions.
• Solve a formula for a given variable.

In this section, we will study linear equations in one variable. There are several real-world scenarios that can be represented by linear equations: taxi rentals with a flat fee and a rate per mile; cell phone bills that charge a monthly fee plus a separate rate per text; gym memberships with a monthly fee plus a rate per class taken; etc. For example, if you join your local gym at $10 per month and pay $5 per class, how many classes can you take if your gym budget is $75 per month?

Linear Equations and Applications

Solving any equation is like discovering the answer to a puzzle. The purpose of solving an equation is to find the value or values of the variable that makes the equation a true statement. Any value of the variable that makes the equation true is called a solution to the equation. It is the answer to the puzzle! There are many types of equations that we will learn to solve. In this section, we will focus on a linear equation , which is an equation in one variable that can be written as

where a a and b b are real numbers and a ≠ 0 a ≠ 0 , such that a a is the coefficient of x x and b b is the constant.

To solve a linear equation, it is a good idea to have an overall strategy that can be used to solve any linear equation. In the Example 5.12, we will give the steps of a general strategy for solving any linear equation. Simplifying each side of the equation as much as possible first makes the rest of the steps easier.

Example 5.12

Solving a linear equation using a general strategy.

Solve 7 ( n − 3 ) − 8 = − 15 7 ( n − 3 ) − 8 = − 15

Your Turn 5.12

In Example 5.12 , we used both the addition and division property of equations. All the properties of equations are summarized in table below. Basically, what you do to one side of the equation, you must do to the other side of the equation to preserve equality.

Be careful to multiply and divide every term on each side of the equation. For example, 2 + x = x 3 2 + x = x 3 is solved by multiplying BOTH sides of the equation by 3 to get 3 ( 2 + x ) = 3 ( x 3 ) 3 ( 2 + x ) = 3 ( x 3 ) which gives 6 + 3 x = x 6 + 3 x = x . Using parentheses will help you remember to use the distributive property! A division example, such as 3 ( x + 2 ) = 6 x + 9 3 ( x + 2 ) = 6 x + 9 , can be solved by dividing BOTH sides of the equation by 3 to get 3 ( x + 2 ) 3 = 6 x + 9 3 , 3 ( x + 2 ) 3 = 6 x + 9 3 , which then will lead to x + 2 = 2 x + 3 x + 2 = 2 x + 3 .

Example 5.13

Solving a linear equation using properties of equations.

Solve 9 ( y − 2 ) − y = 16 + 7 y 9 ( y − 2 ) − y = 16 + 7 y .

Step 1: Simplify each side.

Step 2: Collect all variables on one side.

Step 3: Collect constant terms on one side.

Step 4: Make the coefficient of the variable 1. Already done!

Step 5: Check.

Your Turn 5.13

Who invented the symbol for equals .

Before the creation of a symbol for equality, it was usually expressed with a word that meant equals, such as aequales (Latin), esgale (French), or gleich (German). Welsh mathematician and physician Robert Recorde is given credit for inventing the modern sign. It first appears in writing in The Whetstone of Witte , a book Recorde wrote about algebra, which was published in 1557. In this book, Recorde states, "I will set as I do often in work use, a pair of parallels, or Gemowe (twin) lines of one length, thus: ===, because no two things can be more equal." Although his version of the sign was a bit longer than the one we use today, his idea stuck and "=" is used throughout the world to indicate equality in mathematics.

In Algebraic Expressions , you translated an English sentence into an equation. In this section, we take that one step further and translate an English paragraph into an equation, and then we solve the equation. We can go back to the opening question in this section: If you join your local gym at $10 per month and pay $5 per class, how many classes can you take if your gym budget is $75 per month? We can create an equation for this scenario and then solve the equation (see Example 5.15 ).

Example 5.14

Constructing a linear equation to solve an application.

The Beaudrie family has two cats, Basil and Max. Together, they weigh 23 pounds. Basil weighs 16 pounds. How much does Max weigh?

Let b b = Basil’s weight and m m = Max’s weight.

We also know that Basil weighs 16 pounds so:

Steps 1 and 2: 16 + m = 23 16 + m = 23

Since both sides are simplified, the variable is on one side of the equation, we start in Step 3 and collect the constants on one side:

Step 4: is already done so we go to Step 5:

Basil weighs 16 pounds and Max weighs 7 pounds.

Your Turn 5.14

Example 5.15, constructing a linear equation to solve another application.

If you join your local gym at $10 per month and pay $5 per class, how many classes can you take if your gym budget is $75 per month?

If we let x x = number of classes, the expression 5 x + 10 5 x + 10 would represent what you pay per month if each class is $5 and there’s a $10 monthly fee per class. $10 is your constant. If you want to know how many classes you can take if you have a $75 monthly gym budget, set the equation equal to 75. Then solve the equation 5 x + 10 = 75 5 x + 10 = 75 for x x .

Steps 1 and 2:

The solution is 13 classes. You can take 13 classes on a $75 monthly gym budget.

Your Turn 5.15

Example 5.16, constructing an application from a linear equation.

Write an application that can be solved using the equation 50 x + 35 = 185 50 x + 35 = 185 . Then solve your application.

Answers will vary. Let’s say you want to rent a snowblower for a huge winter storm coming up. If x x = the number of days you rent a snowblower, then the expression 50 x + 35 50 x + 35 represents what you pay if, for each day, it costs $50 to rent the snowblower and there is a $35 flat rental fee. $35 is the constant. To find out how many days you can rent a snowblower for $185, set the expression equal to 185. Then solve the equation 50 x + 35 = 185 50 x + 35 = 185 for x x .

The equation is 50 x + 35 = 185 50 x + 35 = 185 and the solution is 3 days. You can rent a snowblower for 3 days on a $185 budget.

Your Turn 5.16

Linear equations with no solutions or infinitely many solutions.

Every linear equation we have solved thus far has given us one numerical solution. Now we'll look at linear equations for which there are no solutions or infinitely many solutions.

Example 5.17

Solving a linear equation with no solution.

Solve 3 ( x + 4 ) = 4 x + 8 − x 3 ( x + 4 ) = 4 x + 8 − x .

Step 1: Simplify each side. 3 ( x + 4 ) = 4 x + 8 − x 3 ( x + 4 ) = 4 x + 8 − x

Step 2: Collect all variables to one side. 3 x + 12 − 3 x = 3 x + 8 − 3 x 3 x + 12 − 3 x = 3 x + 8 − 3 x

The variable x x disappeared! When this happens, you need to examine what remains. In this particular case, we have 12 = 8 12 = 8 , which is not a true statement. When you have a false statement, then you know the equation has no solution; there does not exist a value for x x that can be put into the equation that will make it true.

Your Turn 5.17

Example 5.18, solving a linear equation with infinitely many solutions.

Solve 2 ( x + 5 ) = 4 ( x + 3 ) − 2 x − 2 2 ( x + 5 ) = 4 ( x + 3 ) − 2 x − 2 .

As with the previous example, the variable disappeared. In this case, however, we have a true statement ( 10 = 10 10 = 10 ). When this occurs we say there are infinitely many solutions; any value for x x will make this statement true.

Your Turn 5.18

Solving a formula for a given variable.

You are probably familiar with some geometry formulas. A formula is a mathematical description of the relationship between variables. Formulas are also used in the sciences, such as chemistry, physics, and biology. In medicine they are used for calculations for dispensing medicine or determining body mass index. Spreadsheet programs rely on formulas to make calculations. It is important to be able to manipulate formulas and solve for specific variables.

To solve a formula for a specific variable means to isolate that variable on one side of the equal sign with a coefficient of 1. All other variables and constants are on the other side of the equal sign. To see how to solve a formula for a specific variable, we will start with the distance, rate, and time formula.

Example 5.19

Solving for a given variable with distance, rate, and time.

Solve the formula d = r t d = r t for t t . This is the distance formula where d d = distance, r r = rate, and t t = time.

Divide both sides by r r : d / r = r t / r d / r = r t / r

d / r = t d / r = t

Your Turn 5.19

Solving for a Variable in an Equation

Example 5.20

Solving for a given variable in the area formula for a triangle.

Solve the formula A = ½ A = ½ bh bh for h h . This is the area formula of a triangle where A A = area, b b = base, and h h = height.

Step 1: Multiply both sides by 2.

Step 2: Divide both sides by b b .

Your Turn 5.20

Work it out, using algebra to understand card tricks.

You will need to perform this card trick with another person. Before you begin, the two people must first decide which of the two will be the Dealer and which will be the Partner , as each will do something different. Once you have decided upon that, follow the steps here:

Step 1: Dealer and Partner: Take a regular deck of 52 cards, and remove the face cards and the 10s.

Step 2: Dealer and Partner: Shuffle the remaining cards

Step 3: Dealer and Partner: Select one card each, but keep them face down and don’t look at them yet.

Step 4: Dealer: Look at your card (just the Dealer!). Multiply its value by 2 (Aces = 1).

Step 5: Dealer: Add 2 to this result.

Step 6: Dealer: Multiply your answer by 5.

Step 7: Partner: Look at your card.

Step 8: Partner: Calculate: 10 - your card, and tell this information to the dealer.

Step 9: Dealer: Subtract the value the Partner tells you from your total to get a final answer.

Step 10: Dealer: verbally state the final answer.

Step 11: Dealer and Partner: Turn over your cards. Now, answer the following questions

• Did the trick work? How do you know?
• Why did this occur? In other words, how does this trick work?

Check Your Understanding

• F = 5 9 C − 32
• F = 9 5 C − 32
• F = 5 9 C + 32
• F = 9 5 C + 32
• C = K + 273
• K = C + 273
• K = C − 273
• C = K − 273
• K = 5 9 ( F − 32 ) + 273
• K = 5 9 F + 241
• K = 9 5 ( F − 32 ) + 273
• K = 9 5 F + 241
• R = 5 9 C − 492
• R = 9 5 C + 492
• R = C + 492
• R = 5 9 ( C − 492 )

Section 5.2 Exercises

As an Amazon Associate we earn from qualifying purchases.

This book may not be used in the training of large language models or otherwise be ingested into large language models or generative AI offerings without OpenStax's permission.

Want to cite, share, or modify this book? This book uses the Creative Commons Attribution License and you must attribute OpenStax.

Access for free at https://openstax.org/books/contemporary-mathematics/pages/1-introduction

• Authors: Donna Kirk
• Publisher/website: OpenStax
• Book title: Contemporary Mathematics
• Publication date: Mar 22, 2023
• Location: Houston, Texas
• Book URL: https://openstax.org/books/contemporary-mathematics/pages/1-introduction
• Section URL: https://openstax.org/books/contemporary-mathematics/pages/5-2-linear-equations-in-one-variable-with-applications

© Dec 21, 2023 OpenStax. Textbook content produced by OpenStax is licensed under a Creative Commons Attribution License . The OpenStax name, OpenStax logo, OpenStax book covers, OpenStax CNX name, and OpenStax CNX logo are not subject to the Creative Commons license and may not be reproduced without the prior and express written consent of Rice University.

Chapter 2 Equations and Inequalities

2.1 Linear Equations in One Variable

Learning objectives.

In this section you will:

• Solve equations in one variable.
• Solve a rational equation.

Caroline is a full-time college student planning a spring break vacation. To earn enough money for the trip, she has taken a part-time job at the local bank that pays $15.00/hr, and she opened a savings account with an initial deposit of $400 on January 15. She arranged for direct deposit of her payroll checks. If spring break begins March 20 and the trip will cost approximately $2,500, how many hours will she have to work to earn enough to pay for her vacation? If she can only work 4 hours per day, how many days per week will she have to work? How many weeks will it take? In this section, we will investigate problems like this and others, which generate graphs like the line in Figure 1.

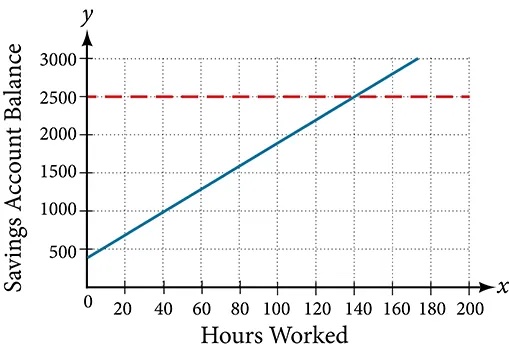
Solving Linear Equations in One Variable

A linear equation is an equation of a straight line, written in one variable. The only power of the variable is 1. Linear equations in one variable may take the form[latex]\,ax+b=0\,[/latex]and are solved using basic algebraic operations.

We begin by classifying linear equations in one variable as one of three types: identity, conditional, or inconsistent. An identity equation is true for all values of the variable. Here is an example of an identity equation.

The solution set consists of all values that make the equation true. For this equation, the solution set is all real numbers because any real number substituted for[latex]\,x\,[/latex]will make the equation true.

A conditional equation is true for only some values of the variable. For example, if we are to solve the equation[latex]\,5x+2=3x-6,[/latex] we have the following:

The solution set consists of one number:[latex]\,\left\{-4\right\}.\,[/latex]It is the only solution, and therefore, we have solved a conditional equation.

An inconsistent equation results in a false statement. For example, if we are to solve[latex]\,5x-15=5\left(x-4\right),[/latex] we have the following:

Indeed,[latex]\,-15\ne \,-20.\,[/latex]There is no solution because this is an inconsistent equation.

Solving linear equations in one variable involves the fundamental properties of equality and basic algebraic operations. A brief review of those operations follows.

Linear Equation in One Variable

A linear equation in one variable can be written in the form

where a and b are real numbers,[latex]\,a\ne 0.[/latex]

Given a linear equation in one variable, use algebra to solve it.

The following steps are used to manipulate an equation and isolate the unknown variable, so that the last line reads[latex]\,x=\text{_________,}[/latex] if x is the unknown. There is no set order, as the steps used depend on what is given:

• We may add, subtract, multiply, or divide an equation by a number or an expression as long as we do the same thing to both sides of the equal sign. Note that we cannot divide by zero.
• Apply the distributive property as needed:[latex]\,a\left(b+c\right)=ab+ac.[/latex]
• Isolate the variable on one side of the equation.
• When the variable is multiplied by a coefficient in the final stage, multiply both sides of the equation by the reciprocal of the coefficient.

Solving an Equation in One Variable

Solve the following equation:[latex]\,2x+7=19.[/latex]

This equation can be written in the form[latex]\,ax+b=0\,[/latex]by subtracting[latex]\,19\,[/latex]from both sides. However, we may proceed to solve the equation in its original form by performing algebraic operations.

The solution is 6

Solve the linear equation in one variable:[latex]\,2x+1=-9.[/latex]

[latex]x=-5[/latex]

Solving an Equation Algebraically When the Variable Appears on Both Sides

Solve the following equation: 4( x – 3) + 12 = 15 – 5 ( x + 6) 

Apply standard algebraic properties.

This problem requires the distributive property to be applied twice, and then the properties of algebra are used to reach the final line,[latex]\,x=-\frac{5}{3}.[/latex]

Solve the equation in one variable:[latex]\,-2\left(3x-1\right)+x=14-x.[/latex]

[latex]x=-3[/latex]

Solving a Rational Equation

In this section, we look at rational equations that, after some manipulation, result in a linear equation. If an equation contains at least one rational expression, it is considered a rational equation .

Recall that a rational number is the ratio of two numbers, such as[latex]\,\frac{2}{3}\,[/latex]or[latex]\,\frac{7}{2}.\,[/latex]A rational expression is the ratio, or quotient, of two polynomials. Here are three examples.

Rational equations have a variable in the denominator in at least one of the terms. Our goal is to perform algebraic operations so that the variables appear in the numerator. In fact, we will eliminate all denominators by multiplying both sides of the equation by the least common denominator (LCD).

Finding the LCD is identifying an expression that contains the highest power of all of the factors in all of the denominators. We do this because when the equation is multiplied by the LCD, the common factors in the LCD and in each denominator will equal one and will cancel out.

Solve the rational equation:[latex]\,\frac{7}{2x}-\frac{5}{3x}=\frac{22}{3}.[/latex]

We have three denominators;[latex]\,2x,3x,[/latex]and 3. The LCD must contain[latex]\,2x,3x,[/latex]and 3. An LCD of[latex]\,6x\,[/latex]contains all three denominators. In other words, each denominator can be divided evenly into the LCD. Next, multiply both sides of the equation by the LCD[latex]\,6x.[/latex]

A common mistake made when solving rational equations involves finding the LCD when one of the denominators is a binomial—two terms added or subtracted—such as[latex]\,\left(x+1\right).\,[/latex]Always consider a binomial as an individual factor—the terms cannot be separated. For example, suppose a problem has three terms and the denominators are[latex]\,x,[/latex][latex]x-1,[/latex] and[latex]\,3x-3.\,[/latex]First, factor all denominators. We then have[latex]\,x,[/latex][latex]\left(x-1\right),[/latex]and[latex]\,3\left(x-1\right)\,[/latex]as the denominators. (Note the parentheses placed around the second denominator.) Only the last two denominators have a common factor of[latex]\,\left(x-1\right).\,[/latex]The[latex]\,x\,[/latex]in the first denominator is separate from the[latex]\,x\,[/latex]in the[latex]\,\left(x-1\right)\,[/latex]denominators. An effective way to remember this is to write factored and binomial denominators in parentheses, and consider each parentheses as a separate unit or a separate factor. The LCD in this instance is found by multiplying together the[latex]\,x,[/latex] one factor of[latex]\,\left(x-1\right),[/latex] and the 3. Thus, the LCD is the following:

So, both sides of the equation would be multiplied by[latex]\,3x\left(x-1\right).\,[/latex]Leave the LCD in factored form, as this makes it easier to see how each denominator in the problem cancels out.

Another example is a problem with two denominators, such as[latex]\,x\,[/latex]and[latex]\,{x}^{2}+2x.\,[/latex]Once the second denominator is factored as[latex]\,{x}^{2}+2x=x\left(x+2\right),[/latex] there is a common factor of x in both denominators and the LCD is[latex]\,x\left(x+2\right).[/latex]

Sometimes we have a rational equation in the form of a proportion—that is, when one fraction equals another fraction and there are no other terms in the equation.

We can use another method of solving the equation without finding the LCD: cross-multiplication. We multiply terms by crossing over the equal sign.

Multiply[latex]\,a\left(d\right)\,[/latex]and[latex]\,b\left(c\right),[/latex] which results in[latex]\,ad=bc.[/latex]

Any solution that makes a denominator in the original expression equal zero must be excluded from the possibilities.

Rational Equations

A rational equation contains at least one rational expression where the variable appears in at least one of the denominators.

Given a rational equation, solve it.

• Factor all denominators in the equation.
• Find and exclude values that set each denominator equal to zero.
• Find the LCD.
• Multiply the whole equation by the LCD. If the LCD is correct, there will be no denominators left.
• Solve the remaining equation.
• Make sure to check solutions back in the original equations to avoid a solution producing zero in a denominator

Solving a Rational Equation without Factoring

Solve the following rational equation:

We have three denominators:[latex]\,x,[/latex][latex]2,[/latex]and[latex]\,2x.\,[/latex]No factoring is required. The product of the first two denominators is equal to the third denominator, so, the LCD is[latex]\,2x.\,[/latex]Only one value is excluded from a solution set, 0.[latex][/latex] Next, multiply the whole equation (both sides of the equal sign) by[latex]\,2x.[/latex]

The proposed solution is −1,[latex][/latex] which is not an excluded value, so the solution set contains one number,[latex]\,x=-1,[/latex]or[latex]\,\left\{-1\right\}\,[/latex]written in set notation.

Solve the rational equation:[latex]\,\frac{2}{3x}=\frac{1}{4}-\frac{1}{6x}.[/latex]

[latex]x=\frac{10}{3}[/latex]

Solving a Rational Equation by Factoring the Denominator

Solve the following rational equation:[latex]\,\frac{1}{x}=\frac{1}{10}-\frac{3}{4x}.[/latex]

First find the common denominator. The three denominators in factored form are[latex]\,x,10=2\cdot 5,[/latex] and[latex]\,4x=2\cdot 2\cdot x.\,[/latex]The smallest expression that is divisible by each one of the denominators is[latex]\,20x.\,[/latex]Only[latex]\,x=0\,[/latex]is an excluded value. Multiply the whole equation by[latex]\,20x.[/latex]

The solution is[latex]\,\frac{35}{2}.[/latex]

Solve the rational equation:[latex]\,-\frac{5}{2x}+\frac{3}{4x}=-\frac{7}{4}.[/latex]

[latex]x=1[/latex]

Solving Rational Equations with a Binomial in the Denominator

Solve the following rational equations and state the excluded values:

• [latex]\frac{3}{x-6}=\frac{5}{x}[/latex]
• [latex]\frac{x}{x-3}=\frac{5}{x-3}-\frac{1}{2}[/latex]
• [latex]\frac{x}{x-2}=\frac{5}{x-2}-\frac{1}{2}[/latex]

The denominators[latex]\,x\,[/latex]and[latex]\,x-6\,[/latex]have nothing in common. Therefore, the LCD is the product[latex]\,x\left(x-6\right).\,[/latex]However, for this problem, we can cross-multiply.

The solution is 15.[latex][/latex] The excluded values are [latex]6[/latex] and [latex]0.[/latex]

The LCD is[latex]\,2\left(x-3\right).\,[/latex]Multiply both sides of the equation by[latex]\,2\left(x-3\right).[/latex]

The solution is[latex]\,\frac{13}{3}.\,[/latex]The excluded value is [latex]3.[/latex]

The least common denominator is[latex]\,2\left(x-2\right).\,[/latex]Multiply both sides of the equation by[latex]\,x\left(x-2\right).[/latex]

The solution is 4. The excluded value is [latex]2.[/latex]

Solve[latex]\,\frac{-3}{2x+1}=\frac{4}{3x+1}.\,[/latex]State the excluded values.

[latex]x=-\frac{7}{17}.\,[/latex]Excluded values are[latex]\,x=-\frac{1}{2}\,[/latex]and[latex]\,x=-\frac{1}{3}.[/latex]

Solving a Rational Equation with Factored Denominators and Stating Excluded Values

Solve the rational equation after factoring the denominators:[latex]\,\frac{2}{x+1}-\frac{1}{x-1}=\frac{2x}{{x}^{2}-1}.\,[/latex]State the excluded values.

We must factor the denominator[latex]\,{x}^{2}-1.\,[/latex]We recognize this as the difference of squares, and factor it as[latex]\,\left(x-1\right)\left(x+1\right).\,[/latex]Thus, the LCD that contains each denominator is[latex]\,\left(x-1\right)\left(x+1\right).\,[/latex]Multiply the whole equation by the LCD, cancel out the denominators, and solve the remaining equation.

The solution is [latex]\,-3.\,[/latex]The excluded values are [latex]\,1\,[/latex] and [latex]\,-1.[/latex]

Solve the rational equation:[latex]\,\frac{2}{x-2}+\frac{1}{x+1}=\frac{1}{{x}^{2}-x-2}.[/latex]

[latex]x=\frac{1}{3}[/latex]

Key Concepts

• We can solve linear equations in one variable in the form[latex]\,ax+b=0\,[/latex]using standard algebraic properties.
• A rational expression is a quotient of two polynomials. We use the LCD to clear the fractions from an equation.
• All solutions to a rational equation should be verified within the original equation to avoid an undefined term, or zero in the denominator.

Section Exercises

• What does it mean when we say that a linear equation is inconsistent?
• When solving the following equation:  [latex]\frac{2}{x-5}=\frac{4}{x+1}[/latex] explain why we must exclude[latex]\,x=5\,[/latex]and[latex]\,x=-1\,[/latex]as possible solutions from the solution set.

If we insert either value into the equation, they make an expression in the equation undefined (zero in the denominator).

For the following exercises, solve the equation for[latex]\,x.[/latex]

• [latex]7x+2=3x-9[/latex]
• [latex]4x-3=5[/latex]

[latex]x=2[/latex]

• [latex]3\left(x+2\right)-12=5\left(x+1\right)[/latex]
• [latex]12-5\left(x+3\right)=2x-5[/latex]

[latex]x=\frac{2}{7}[/latex]

• [latex]\frac{1}{2}-\frac{1}{3}x=\frac{4}{3}[/latex]
• [latex]\frac{x}{3}-\frac{3}{4}=\frac{2x+3}{12}[/latex]

[latex]x=6[/latex]

• [latex]\frac{2}{3}x+\frac{1}{2}=\frac{31}{6}[/latex]
• [latex]3\left(2x-1\right)+x=5x+3[/latex]

[latex]x=3[/latex]

• [latex]\frac{2x}{3}-\frac{3}{4}=\frac{x}{6}+\frac{21}{4}[/latex]
• [latex]\frac{x+2}{4}-\frac{x-1}{3}=2[/latex]

[latex]x=-14[/latex]

For the following exercises, solve each rational equation for[latex]\,x.\,[/latex]State all x -values that are excluded from the solution set.

• [latex]\frac{3}{x}-\frac{1}{3}=\frac{1}{6}[/latex]
• [latex]2-\frac{3}{x+4}=\frac{x+2}{x+4}[/latex]

[latex]x\ne -4;[/latex][latex]x=-3[/latex]

• [latex]\frac{3}{x-2}=\frac{1}{x-1}+\frac{7}{\left(x-1\right)\left(x-2\right)}[/latex]
• [latex]\frac{3x}{x-1}+2=\frac{3}{x-1}[/latex]

[latex]x\ne 1;[/latex]when we solve this we get[latex]\,x=1,[/latex]which is excluded, therefore NO solution

• [latex]\frac{5}{x+1}+\frac{1}{x-3}=\frac{-6}{{x}^{2}-2x-3}[/latex]
• [latex]\frac{1}{x}=\frac{1}{5}+\frac{3}{2x}[/latex]

[latex]x\ne 0;[/latex][latex]x=\frac{-5}{2}[/latex]

Media Attributions

• 2.1 Figure 1 © OpenStax Algebra and Trigonometry is licensed under a CC BY (Attribution) license
• 2.1 Proportion Graphic © OpenStax Algebra and Trignometry is licensed under a CC BY (Attribution) license

College Algebra Copyright © 2024 by LOUIS: The Louisiana Library Network is licensed under a Creative Commons Attribution 4.0 International License , except where otherwise noted.

Share This Book

NEW CHAPTER 6 Linear Equations and Inequalities in One Variable

6.1.1 solving linear equations in one variable, solving linear equations, learning objectives.

• Determine whether or not an equation in one variable is defined as a linear equation
• Use the addition and subtraction property to solve a linear equation
• Use the multiplication and division property to solve a linear equation
• Equality : The state of two or more entities having the same value.
• Equation : a statement that two expressions are equal.
• Solution : a number or numbers that make an equation true.
• Equivalent equations: two or more equations that have identical solutions.

Linear Equations

An equation with just one variable is said to be  linear when the highest power on the variable is [latex]1[/latex]. Remember that [latex]{x}^{1}[/latex] is equivalent to [latex]x[/latex], so any equation that can be simplified to [latex]ax+b=c[/latex] (where [latex]a,b,c[/latex] are real numbers) is a linear equation in one variable . For example, the equation [latex]2x+3=7, \;5x=7,\; -\frac{3}{4}x+\frac{7}{3}=\frac{6}{5}[/latex] are all linear equations because the highest power of [latex]x[/latex] is [latex]1[/latex]. On the other hand, the equation [latex]{x}^3+2{x}^2=4x-2[/latex] is NOT linear because the highest power of [latex]x[/latex] is [latex]3[/latex], not [latex]1[/latex].

Determine whether the equation is linear:

a) [latex]3x-7=6x+2[/latex]

b) [latex]{x}^{3}-5{x}^{2}=5x+6[/latex]

c) [latex]x(x+6)=8[/latex]

d) [latex]x-\frac{3}{8} =\frac{1}{2}[/latex]

Determine whether the equation [latex]6x-7=8{x}^{2}+5[/latex] is linear.

[latex]6x-7=8{x}^{2}+5[/latex] is NOT linear since the highest power of [latex]x[/latex] is [latex]2[/latex], not [latex]1[/latex].

Determine whether the equation [latex]\frac{4}{5}x+6=\frac{-7}{3}x[/latex] is linear.

[latex]\frac{4}{5}x+6=\frac{-7}{3}x[/latex] is linear since the highest power of [latex]x[/latex] is [latex]1[/latex].

The Addition and Subtraction Property of Equality

When an equation contains a variable such as [latex]x[/latex], this variable is considered an unknown value. In many cases, we can find the possible values for [latex]x[/latex] that would make the equation true. We can  solve  the equation for [latex]x[/latex].

For some equations like [latex]x + 3 =5[/latex] it is easy to guess the solution: the only possible value of [latex]x[/latex] is [latex]2[/latex], because [latex]2 + 3 = 5[/latex]. However, it becomes useful to have a process for finding solutions for unknowns as problems become more complex.

In order to solve an equation, we need to  isolate the variable . Isolating the variable means rewriting an equivalent equation in which the variable is on one side of the equation and everything else is on the other side of the equation. The variable is an unknown quantity whose value we are trying to find. We have a solution when we reorganize the equation into the form [latex]x[/latex] = a constant.

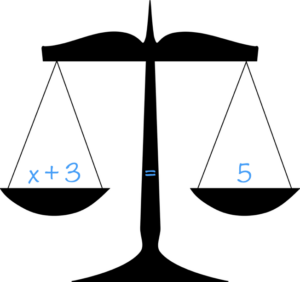
The second we add or subtract a “weight” to one side of the scale, it will become unbalanced. In order to right that balance, we must add or subtract the same “weight” to the other side of the sale.

To solve this equation for [latex]x[/latex], we need to isolate [latex]x[/latex] by removing the [latex]+3[/latex] from the left side of the equation. We do this this by “undoing” the addition of [latex]+3[/latex] by subtracting [latex]3[/latex].  In other words we use the inverse operation of addition, which is subtraction. But if we subtract [latex]3[/latex] from the left side of the equation, we must also subtract [latex]3[/latex] from the right side to keep the equation balanced.

[latex]x+3\;\;\;\;\;\;=5 \\ x+3\color{blue}{-3}=5\color{blue}{-3} \\ x\;\;\;\;\;\;\;\;\;\;\;\;\,=2[/latex]

We can verify that [latex]x=2[/latex] is indeed the solution by substituting [latex]2[/latex] in for [latex]x[/latex] in the original equation: [latex]x+3=5 \\ 2+3=5 \\ 5=5[/latex] Since this is true, [latex]x=2[/latex] is the solution of [latex]x+3=5[/latex].

If the equation is [latex]x-5=9[/latex], we isolate the variable by adding [latex]5[/latex] to both sides of the equation. This is because, to isolate [latex]x[/latex] we must “undo” subtract [latex]5[/latex] by adding [latex]5[/latex]: 

[latex]x-5=9 \\ x-5\color{blue}{+5}=9\color{blue}{+5} \\ x\;\;\;\;\;\;\;\;\;\;\;\;\,=14[/latex]

Again, we can verify the solution: [latex]x-5\;\;\;\;\;\;=9 \\ 14 - 5 = 9 \\ 9=9[/latex] True.

When we add or subtract the same term to both sides of an equation, we get an equivalent equation . Equivalent equations are two or more equations that have identical solutions. This leads us to the the Addition and Subtraction Property of Equality .

Addition & subtraction Property of Equality

For all real numbers [latex]a,b[/latex], and [latex]c[/latex], if [latex]a=b[/latex], then [latex]a+c=b+c[/latex] and [latex]a-c=b-c[/latex].

Adding or subtracting the same term to both sides of an equation will result in an equivalent equation .

Solve: [latex]x+11=-3[/latex]

Solution: To isolate [latex]x[/latex], we undo the addition of [latex]11[/latex] by using the Subtraction Property of Equality.

Since [latex]x=-14[/latex] makes [latex]x+11=-3[/latex] a true statement, we know that it is a solution to the equation.

https://ohm.lumenlearning.com/multiembedq.php?id=141721&theme=oea&iframe_resize_id=mom200

Solve: [latex]m - 4=-5[/latex]

https://ohm.lumenlearning.com/multiembedq.php?id=141723&theme=oea&iframe_resize_id=mom27

Linear Equations Containing Fractions

It is not uncommon to encounter equations that contain fractions; therefore, in the following examples, we will demonstrate how to use the addition property of equality to solve an equation with fractions.

Solve: [latex]n-\frac{3}{8} =\frac{1}{2}[/latex]

https://ohm.lumenlearning.com/multiembedq.php?id=141732&theme=oea&iframe_resize_id=mom25

Watch this video for more examples of solving equations that include fractions and require addition or subtraction.

Linear Equations Containing Decimals

Decimals will be encountered any time money or metric measurements are used.

Solve [latex]a - 3.7=4.3[/latex]

https://ohm.lumenlearning.com/multiembedq.php?id=141736&theme=oea&iframe_resize_id=mom29

The Multiplication and Division Properties of Equality

Just as we can add or subtract the same exact quantity on both sides of an equation, we can also multiply or divide both sides of an equation by the same quantity to write an equivalent equation. This makes sense because multiplication is just repeated addition and division is multiplication by a reciprocal.

For example, to solve the equation [latex]3x=15[/latex] we need to isolate the variable [latex]x[/latex] which is multiplied by [latex]3[/latex]. To “undo” this multiplication, we divide both sides of the equation by [latex]3[/latex]:  [latex]\frac{3x}\color{blue}{{3}}=\frac{15}\color{blue}{{3}}[/latex]. Since [latex]\frac{3}{3}=1[/latex] and [latex]1x=x[/latex], this simplifies to [latex]x=5[/latex] and we have our solution.

On the other hand, in the equation [latex]\frac{1}{2}x=-5[/latex] the variable [latex]x[/latex] is multiplied by [latex]\frac{1}{2}[/latex]. To isolate the variable we need to turn [latex]\frac{1}{2}[/latex] into [latex]1[/latex] by multiplying by the reciprocal [latex]2[/latex]:     [latex]\color{blue}{2}\left(\frac{1}{2}x\right)=\color{blue}{2}(-5)[/latex]. This simplifies to [latex]x=-10[/latex] and we have our solution.

This characteristic of equations is generalized in the M ultiplication & Division Property of Equality .

multiplication & Division Property of Equality

For all real numbers [latex]a,b,c[/latex], and [latex]c\ne 0[/latex], if [latex]a=b[/latex], then [latex]ac=bc[/latex] and [latex]\Large\frac{a}{c}\normalsize =\Large\frac{b}{c}[/latex].

Multiplying or dividing the same non-zero* term to both sides of an equation will result in an equivalent equation .

*Technically we could multiply both sides of an equation by zero but that would wipe out our entire equation to [latex]0=0[/latex]. However, we can never divide by zero as that is undefined.

When the equation involves multiplication or division, we can “undo” these operations by using the inverse operation to isolate the variable.

Solve [latex]3x=24[/latex]. When you are done, check your solution.

Divide both sides of the equation by [latex]3[/latex] to isolate the variable (this is will give you a coefficient of  [latex]1[/latex]). Dividing by [latex]3[/latex] is the same as multiplying by [latex] \frac{1}{3}[/latex].

[latex]\begin{array}{r}\underline{3x}=\underline{24}\\3\,\,\,\,\,\,\,\,\,\,\,\,3\,\\x=8\,\,\,\end{array}[/latex]

Check by substituting your solution, [latex]8[/latex], for the variable in the original equation.

[latex]\begin{array}{r}3x=24 \\ 3\cdot8=24 \\ 24=24\end{array}[/latex]

The solution is correct!

[latex]x=8[/latex]

Solve: [latex]\frac{a}{-7} =-42[/latex]

Solution Here [latex]a[/latex] is divided by [latex]-7[/latex]. We can multiply both sides by [latex]-7[/latex] to isolate [latex]a[/latex].

https://ohm.lumenlearning.com/multiembedq.php?id=141868&theme=oea&iframe_resize_id=mom21

Another way to think about solving an equation when the operation is multiplication or division is that we want to multiply the coefficient by the multiplicative inverse (reciprocal) in order to change the coefficient to [latex]1[/latex].

In the following example, we change the coefficient to  [latex]1[/latex] by multiplying by the multiplicative inverse of [latex]\frac{1}{2}[/latex].

Solve [latex] \frac{1}{2}x=8[/latex] for [latex]x[/latex].

We can multiply both sides by the reciprocal of [latex]\frac{1}{2}[/latex], which is [latex]\frac{2}{1}[/latex].

[latex]\begin{array}{r}\color{blue}{\left(\frac{2}{1}\right)}\frac{1}{2 }{ x }=\color{blue}{\left(\frac{2}{1}\right)}8\\(1)x= 16\,\,\,\,\\{ x }=16\,\,\,\,\,\end{array}[/latex]

The video shows examples of how to use the Multiplication and Division Property of Equality to solve one-step equations with integers and fractions.

Solve: [latex]4x=-28[/latex]

To solve this equation, we use the Division Property of Equality to divide both sides by [latex]4[/latex].

Since this is a true statement, [latex]x=-7[/latex] is a solution to [latex]4x=-28[/latex].

https://ohm.lumenlearning.com/multiembedq.php?id=141857&theme=oea&iframe_resize_id=mom2

As we solve equations that require several steps, it is not unusual to end up with an equation that looks like the one in the next example, with a negative sign in front of the variable.  

Solve: [latex]-r=2[/latex]

Solution: Remember [latex]-r[/latex] is equivalent to [latex]-1r[/latex].

https://ohm.lumenlearning.com/multiembedq.php?id=141865&theme=oea&iframe_resize_id=mom22

The equations [latex]x=4[/latex] and [latex]4=x[/latex] are equivalent. Both say that [latex]x[/latex] is equal to [latex]4[/latex]. This is an example of The Reflection Property of Equality .

The Reflection Property of Equality

If [latex]a=b[/latex], then [latex]b=a[/latex], for all real numbers [latex]a[/latex] and [latex]b[/latex].

This implies that it does not matter which side of the equation the variable term ends up on.

The next video includes examples of using the division and multiplication properties to solve equations with the variable on the right side of the equal sign.

Two-Step Linear Equations

If the equation is in the form [latex]ax+b=c[/latex], where [latex]x[/latex] is the variable, we can solve the equation as before. First we must isolate the [latex]x-[/latex]term by “undoing” the addition or subtraction. Then we isolate the variable by “undoing” the multiplication or division.

1. Solve: [latex]4x+6=-14[/latex]

In this equation, the variable is only on the left side. It makes sense to call the left side the variable side. Therefore, the right side will be the constant side.

2. Solve: [latex]2y - 7=15[/latex]

Solution: Notice that the variable is only on the left side of the equation, so this will be the variable side, and the right side will be the constant side. Since the left side is the variable side, the [latex]7[/latex] is out of place. It is subtracted from the [latex]2y[/latex], so to “undo” subtraction, add [latex]7[/latex] to both sides.

Solve [latex]3y+2=11[/latex]

Subtract [latex]2[/latex] from both sides of the equation to get the term with the variable by itself.

[latex] \displaystyle \begin{array}{r}3y+2\,\,\,=\,\,11\\\underline{\,\,\,\,\,\,\,\color{blue}{-2}\,\,\,\,\,\,\,\,\color{blue}{-2}}\\3y\,\,\,\,=\,\,\,\,\,9\end{array}[/latex]

Divide both sides of the equation by [latex]3[/latex] to get a coefficient of [latex]1[/latex] for the variable.

[latex]\begin{array}{r}\,\,\,\,\,\,\underline{3y}\,\,\,\,=\,\,\,\,\,\underline{9}\\3\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,9\\\,\,\,\,\,\,\,\,\,\,y\,\,\,\,=\,\,\,\,3\end{array}[/latex]

[latex]y=3[/latex]

https://ohm.lumenlearning.com/multiembedq.php?id=142131&theme=oea&iframe_resize_id=mom2

In the following video, we show examples of solving two step linear equations.

Remember to check the solution of an algebraic equation by substituting the value of the variable into the original equation.

Privacy Policy

Solving Linear Equations

Solving linear equations means finding the value of the variable(s) given in the linear equations. A linear equation is a combination of an algebraic expression and an equal to (=) symbol. It has a degree of 1 or it can be called a first-degree equation. For example, x + y = 4 is a linear equation. Sometimes, we may have to find the values of variables involved in a linear equation. When we are given two or more such linear equations, we can find the values of each variable by solving linear equations. There are a few methods to solve linear equations. Let us discuss each of these methods in detail.

Solving Linear Equations in One Variable

A linear equation in one variable is an equation of degree one and has only one variable term. It is of the form 'ax+b = 0', where 'a' is a non zero number and 'x' is a variable. By solving linear equations in one variable, we get only one solution for the given variable. An example for this is 3x - 6 = 0. The variable 'x' has only one solution, which is calculated as 3x - 6 = 0 3x = 6 x = 6/3 x = 2

For solving linear equations with one variable, simplify the equation such that all the variable terms are brought to one side and the constant value is brought to the other side. If there are any fractional terms then find the LCM ( Least Common Multiple ) and simplify them such that the variable terms are on one side and the constant terms are on the other side. Let us work out a small example to understand this.

4x + 8 = 8x - 10. To find the value of 'x', let us simplify and bring the 'x' terms to one side and the constant terms to another side.

4x - 8x = -10 - 8 -4x = -18 4x = 18 x = 18/4 On simplifying, we get x = 9/2.

Solving Linear Equations by Substitution Method

The substitution method is one of the methods of solving linear equations. In the substitution method , we rearrange the equation such that one of the values is substituted in the second equation. Now that we are left with an equation that has only one variable, we can solve it and find the value of that variable. In the two given equations, any equation can be taken and the value of a variable can be found and substituted in another equation. For solving linear equations using the substitution method, follow the steps mentioned below. Let us understand this with an example of solving the following system of linear equations. x + y = 6 --------------(1) 2x + 4y = 20 -----------(2)

Step 1: Find the value of one of the variables using any one of the equations. In this case, let us find the value of 'x' from equation (1). x + y = 6 ---------(1) x = 6 - y Step 2: Substitute the value of the variable found in step 1 in the second linear equation. Now, let us substitute the value of 'x' in the second equation 2x + 4y = 20.

x = 6 - y Substituting the value of 'x' in 2x + 4y = 20, we get,

2(6 - y) + 4y = 20 12 - 2y + 4y = 20 12 + 2y = 20 2y = 20 - 12 2y = 8 y = 8/2 y = 4 Step 3: Now substitute the value of 'y' in either equation (1) or (2). Let us substitute the value of 'y' in equation (1).

x + y = 6 x + 4 = 6 x = 6 - 4 x = 2 Therefore, by substitution method, the linear equations are solved, and the value of x is 2 and y is 4.

Solving Linear Equations by Elimination Method

The elimination method is another way to solve a system of linear equations. Here we make an attempt to multiply either the 'x' variable term or the 'y' variable term with a constant value such that either the 'x' variable terms or the 'y' variable terms cancel out and gives us the value of the other variable. Let us understand the steps of solving linear equations by elimination method . Consider the given linear equations: 2x + y = 11 ----------- (1) x + 3y = 18 ---------- (2) Step 1: Check whether the terms are arranged in a way such that the 'x' term is followed by a 'y' term and an equal to sign and after the equal to sign the constant term should be present. The given set of linear equations are already arranged in the correct way which is ax+by=c or ax+by-c=0.

Step 2: The next step is to multiply either one or both the equations by a constant value such that it will make either the 'x' terms or the 'y' terms cancel out which would help us find the value of the other variable. Now in equation (2), let us multiply every term by the number 2 to make the coefficients of x the same in both the equations. x + 3y = 18 ---------- (2) Multiplying all the terms in equation (2) by 2, we get,

2(x) + 2(3y) = 2(18). Now equation (2) becomes, 2x + 6y = 36 -----------(2)

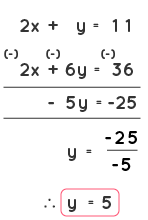
Therefore, y = 5. Step 4: Using the value obtained in step 3, find out the value of another variable by substituting the value in any of the equations. Let us substitute the value of 'y' in equation (1). We get, 2x + y = 11 2x + 5 = 11 2x = 11 - 5 2x = 6 x = 6/2 x = 3

Therefore, by solving linear equations, we get the value of x = 3 and y = 5.

Graphical Method of Solving Linear Equations

Another method for solving linear equations is by using the graph. When we are given a system of linear equations, we graph both the equations by finding values for 'y' for different values of 'x' in the coordinate system. Once it is done, we find the point of intersection of these two lines. The (x,y) values at the point of intersection give the solution for these linear equations. Let us take two linear equations and solve them using the graphical method.

x + y = 8 -------(1)

y = x + 2 --------(2)

Let us take some values for 'x' and find the values for 'y' for the equation x + y = 8. This can also be rewritten as y = 8 - x.

Let us take some values for 'x' and find the values for 'y' in the equation y = x + 2.

Plotting these points on the coordinate plane, we get a graph like this.

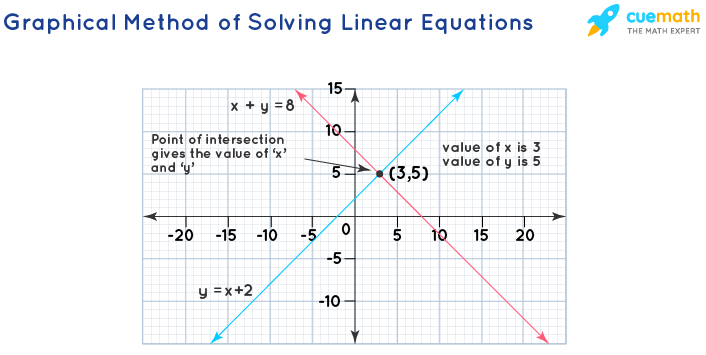
Now, we find the point of intersection of these lines to find the values of 'x' and 'y'. The two lines intersect at the point (3,5). Therefore, x = 3 and y = 5 by using the graphical method of solving linear equations .

This method is also used to find the optimal solution of linear programming problems. Let us look at one more method of solving linear equations, which is the cross multiplication method.

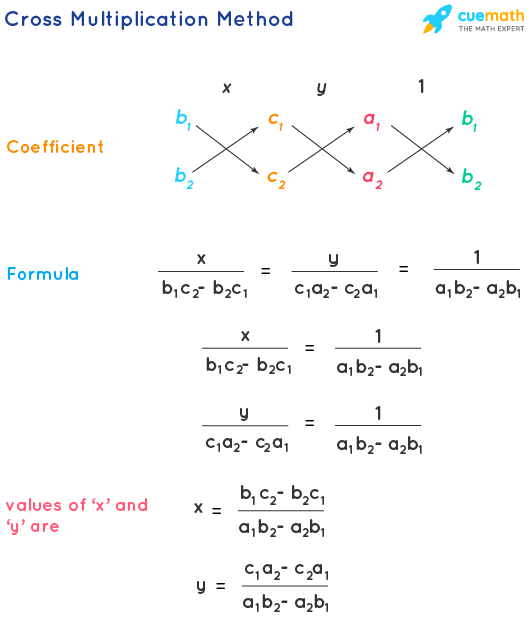
Cross Multiplication Method of Solving Linear Equations

The cross multiplication method enables us to solve linear equations by picking the coefficients of all the terms ('x' , 'y' and the constant terms) in the format shown below and apply the formula for finding the values of 'x' and 'y'.

Topics Related to Solving Linear Equations

Check the given articles related to solving linear equations.

• Linear Equations
• Application of Linear Equations
• Two-Variable Linear Equations
• Linear Equations and Half Planes
• One Variable Linear Equations and Inequations

Solving Linear Equations Examples

Example 1: Solve the following linear equations by the substitution method.

3x + y = 13 --------- (1) 2x + 3y = 18 -------- (2)

By using the substitution method of solving linear equations, let us take the first equation and find the value of 'y' and substitute it in the second equation.

From equation (1), y = 13-3x. Now, substituting the value of 'y' in equation (2), we get, 2x + 3 (13 - 3x) = 18 2x + 39 - 9x = 18 -7x + 39 = 18 -7x = 18 - 39 -7x = -21 x = -21/-7 x = 3 Now, let us substitute the value of 'x = 3' in equation (1) and find the value of 'y'. 3x + y = 13 ------- (1) 3(3) + y = 13 9 + y = 13 y = 13 - 9 y = 4

Therefore, by the substitution method, the value of x is 3 and y is 4.

Example 2: Using the elimination method of solving linear equations find the values of 'x' and 'y'.

3x + y = 21 ------ (1) 2x + 3y = 28 -------- (2)

By using the elimination method, let us make the 'y' variable to be the same in both the equations (1) and (2). To do this let us multiply all the terms of the first equation by 3. Therefore equation (1) becomes,

3(3x) + 3(y) = 63 9x + 3y = 63 ---------- (3) The second equation is, 2x + 3y = 28 Now let us cancel the 'y' terms and find the value of 'x' by subtracting equation (2) from equation (3). This is done by changing the signs of all the terms in equation (2).

Example 3: Using the cross multiplication method of solving linear equations, solve the following equations.

x + 2y - 16 = 0 --------- (1) 4x - y - 10 = 0 ---------- (2)

Compare the given equation with \(a_{1}\)x + \(b_{1}\)y + \(c_{1}\) = 0, and \(a_{2}\)x+\(b_{2}\)y+\(c_{2}\) = 0. From the given equations,

\(a_{1}\) = 1, \(a_{2}\) = 4, \(b_{1}\) = 2, \(b_{2}\) = -1, \(c_{1}\) = -16, and \(c_{2}\) = -10.

By cross multiplication method,

x = \(b_{1}\)\(c_{2}\) - \(b_{2}\)\(c_{1}\)/\(a_{1}\)\(b_{2}\) - \(a_{2}\)\(b_{1}\) y = \(c_{1}\)\(a_{2}\) - \(c_{2}\)\(a_{1}\) / \(a_{1}\)\(b_{2}\) - \(a_{2}\)\(b_{1}\)

Substituting the values in the formula we get,

x = ((2)(-10)) - ((-1)(-16)) / ((1)(-1)) - ((4)(2)) x = (-20-16)/(-1-8) x = -36/-9 x = 36/9 x = 4 y = ((-16)(4)) - ((-10)(1)) / ((1)(-1)) - ((4)(2)) y = (-64 + 10) / (-1 - 8) y = -54 / -9 y = 54/9 y = 6 Therefore, by the cross multiplication method, the value of x is 4 and y is 6.

go to slide go to slide go to slide

Book a Free Trial Class

Practice Questions on Solving Linear Equations

Faqs on solving linear equations, what does it mean by solving linear equations.

An equation that has a degree of 1 is called a linear equation. We can have one variable linear equations , two-variable linear equations , linear equations with three variables, and more depending on the number of variables in it. Solving linear equations means finding the values of all the variables present in the equation. This can be done by substitution method, elimination method, graphical method, and the cross multiplication method . All these methods are different ways of finding the values of the variables.

How to Use the Substitution Method for Solving Linear Equations?

The substitution method of solving equations states that for a given system of linear equations, find the value of either 'x' or 'y' from any of the given equations and then substitute the value found of 'x' or 'y' in another equation so that the other unknown value can be found.

How to Use the Elimination Method for Solving Linear Equations?

In the elimination method of solving linear equations, we multiply a constant or a number with one equation or both the equations such that either the 'x' terms or the 'y' terms are the same. Then we cancel out the same term in both the equations by either adding or subtracting them and find the value of one variable (either 'x' or 'y'). After finding one of the values, we substitute the value in one of the equations and find the other unknown value.

What is the Graphical Method of Solving Linear Equations?

In the graphical method of solving linear equations, we find the value of 'y' from the given equations by putting the values of x as 0, 1, 2, 3, and so on, and plot a graph in the coordinate system for the line for various values of 'x' for both the system of linear equations. We will see that these two lines intersect at a point. This point is the solution for the given system of linear equations. If there is no intersection point between two lines, then we consider them as parallel lines , and if we found that both the lines lie on each other, those are known as coincident lines and have infinitely many solutions.

What are the Steps of Solving Linear Equations that has One Variable?

A linear equation is an equation with degree 1. To solve a linear equation that has one variable we bring the variable to one side and the constant value to the other side. Then, a non-zero number may be added, subtracted, multiplied, or divided on both sides of the equation. For example, a linear equation with one variable will be of the form 'x - 4 = 2'. To find the value of 'x', we add the constant value '4' to both sides of the equation. Therefore, the value of 'x = 6'.

What are the Steps of Solving Linear Equations having Three Variables?

To solve a system of linear equations that has three variables, we take any two equations and variables. We then take another pair of linear equations and also solve for the same variable. Now that, we have two linear equations with two variables, we can use the substitution method or elimination method, or any other method to solve the values of two unknown variables. After finding these two variables, we substitute them in any of the three equations to find the third unknown variable.

What are the 4 Methods of Solving Linear Equations?

The methods for solving linear equations are given below:

• Substitution method
• Elimination method
• Cross multiplication method
• Graphical method

Word Problems on Linear Equations

Worked-out word problems on linear equations with solutions explained step-by-step in different types of examples.

There are several problems which involve relations among known and unknown numbers and can be put in the form of equations. The equations are generally stated in words and it is for this reason we refer to these problems as word problems. With the help of equations in one variable, we have already practiced equations to solve some real life problems.

Steps involved in solving a linear equation word problem: ● Read the problem carefully and note what is given and what is required and what is given. ● Denote the unknown by the variables as x, y, ……. ● Translate the problem to the language of mathematics or mathematical statements. ● Form the linear equation in one variable using the conditions given in the problems. ● Solve the equation for the unknown. ● Verify to be sure whether the answer satisfies the conditions of the problem.

Step-by-step application of linear equations to solve practical word problems:

1. The sum of two numbers is 25. One of the numbers exceeds the other by 9. Find the numbers. 

Solution: Then the other number = x + 9 Let the number be x.  Sum of two numbers = 25 According to question, x + x + 9 = 25 ⇒ 2x + 9 = 25 ⇒ 2x = 25 - 9 (transposing 9 to the R.H.S changes to -9)  ⇒ 2x = 16 ⇒ 2x/2 = 16/2 (divide by 2 on both the sides)  ⇒ x = 8 Therefore, x + 9 = 8 + 9 = 17 Therefore, the two numbers are 8 and 17.

2.The difference between the two numbers is 48. The ratio of the two numbers is 7:3. What are the two numbers?  Solution:   Let the common ratio be x.  Let the common ratio be x.  Their difference = 48 According to the question,  7x - 3x = 48  ⇒ 4x = 48  ⇒ x = 48/4  ⇒ x = 12 Therefore, 7x = 7 × 12 = 84           3x = 3 × 12 = 36  Therefore, the two numbers are 84 and 36.

3. The length of a rectangle is twice its breadth. If the perimeter is 72 metre, find the length and breadth of the rectangle.  Solution: Let the breadth of the rectangle be x,  Then the length of the rectangle = 2x Perimeter of the rectangle = 72 Therefore, according to the question 2(x + 2x) = 72 ⇒ 2 × 3x = 72 ⇒ 6x = 72  ⇒ x = 72/6 ⇒ x = 12 We know, length of the rectangle = 2x                       = 2 × 12 = 24 Therefore, length of the rectangle is 24 m and breadth of the rectangle is 12 m.

4. Aaron is 5 years younger than Ron. Four years later, Ron will be twice as old as Aaron. Find their present ages. 

Solution: Let Ron’s present age be x.  Then Aaron’s present age = x - 5 After 4 years Ron’s age = x + 4, Aaron’s age x - 5 + 4.  According to the question;  Ron will be twice as old as Aaron.  Therefore, x + 4 = 2(x - 5 + 4)  ⇒ x + 4 = 2(x - 1)  ⇒ x + 4 = 2x - 2 ⇒ x + 4 = 2x - 2 ⇒ x - 2x = -2 - 4 ⇒ -x = -6 ⇒ x = 6 Therefore, Aaron’s present age = x - 5 = 6 - 5 = 1 Therefore, present age of Ron = 6 years and present age of Aaron = 1 year.

5. A number is divided into two parts, such that one part is 10 more than the other. If the two parts are in the ratio 5 : 3, find the number and the two parts.  Solution: Let one part of the number be x Then the other part of the number = x + 10 The ratio of the two numbers is 5 : 3 Therefore, (x + 10)/x = 5/3 ⇒ 3(x + 10) = 5x  ⇒ 3x + 30 = 5x ⇒ 30 = 5x - 3x ⇒ 30 = 2x  ⇒ x = 30/2  ⇒ x = 15 Therefore, x + 10 = 15 + 10 = 25 Therefore, the number = 25 + 15 = 40  The two parts are 15 and 25. 

More solved examples with detailed explanation on the word problems on linear equations.

6. Robert’s father is 4 times as old as Robert. After 5 years, father will be three times as old as Robert. Find their present ages.  Solution: Let Robert’s age be x years.  Then Robert’s father’s age = 4x After 5 years, Robert’s age = x + 5 Father’s age = 4x + 5 According to the question,  4x + 5 = 3(x + 5)  ⇒ 4x + 5 = 3x + 15  ⇒ 4x - 3x = 15 - 5  ⇒ x = 10 ⇒ 4x = 4 × 10 = 40  Robert’s present age is 10 years and that of his father’s age = 40 years.  

7. The sum of two consecutive multiples of 5 is 55. Find these multiples.  Solution: Let the first multiple of 5 be x.  Then the other multiple of 5 will be x + 5 and their sum = 55 Therefore, x + x + 5 = 55 ⇒ 2x + 5 = 55 ⇒ 2x = 55 - 5 ⇒ 2x = 50 ⇒ x = 50/2  ⇒ x = 25  Therefore, the multiples of 5, i.e., x + 5 = 25 + 5 = 30 Therefore, the two consecutive multiples of 5 whose sum is 55 are 25 and 30.  

8. The difference in the measures of two complementary angles is 12°. Find the measure of the angles.  Solution: Let the angle be x.  Complement of x = 90 - x Given their difference = 12° Therefore, (90 - x) - x = 12° ⇒ 90 - 2x = 12 ⇒ -2x = 12 - 90 ⇒ -2x = -78 ⇒ 2x/2 = 78/2 ⇒ x = 39 Therefore, 90 - x = 90 - 39 = 51  Therefore, the two complementary angles are 39° and 51°

9. The cost of two tables and three chairs is $705. If the table costs $40 more than the chair, find the cost of the table and the chair.  Solution: The table cost $ 40 more than the chair.  Let us assume the cost of the chair to be x.  Then the cost of the table = $ 40 + x The cost of 3 chairs = 3 × x = 3x and the cost of 2 tables 2(40 + x)  Total cost of 2 tables and 3 chairs = $705 Therefore, 2(40 + x) + 3x = 705 80 + 2x + 3x = 705 80 + 5x = 705 5x = 705 - 80 5x = 625/5 x = 125 and 40 + x = 40 + 125 = 165 Therefore, the cost of each chair is $125 and that of each table is $165. 

10. If 3/5 ᵗʰ of a number is 4 more than 1/2 the number, then what is the number?  Solution: Let the number be x, then 3/5 ᵗʰ of the number = 3x/5 Also, 1/2 of the number = x/2  According to the question,  3/5 ᵗʰ of the number is 4 more than 1/2 of the number.  ⇒ 3x/5 - x/2 = 4 ⇒ (6x - 5x)/10 = 4 ⇒ x/10 = 4 ⇒ x = 40 The required number is 40.  

Try to follow the methods of solving word problems on linear equations and then observe the detailed instruction on the application of equations to solve the problems.

●   Equations

What is an Equation?

What is a Linear Equation?

How to Solve Linear Equations?

Solving Linear Equations

Problems on Linear Equations in One Variable

Word Problems on Linear Equations in One Variable

Practice Test on Linear Equations

Practice Test on Word Problems on Linear Equations

●   Equations - Worksheets

Worksheet on Linear Equations

Worksheet on Word Problems on Linear Equation

7th Grade Math Problems   8th Grade Math Practice   From Word Problems on Linear Equations to HOME PAGE

Didn't find what you were looking for? Or want to know more information about Math Only Math . Use this Google Search to find what you need.

New! Comments

• Preschool Activities
• Kindergarten Math
• 1st Grade Math
• 2nd Grade Math
• 3rd Grade Math
• 4th Grade Math
• 5th Grade Math
• 6th Grade Math
• 7th Grade Math
• 8th Grade Math
• 9th Grade Math
• 10th Grade Math
• 11 & 12 Grade Math
• Concepts of Sets
• Probability
• Boolean Algebra
• Math Coloring Pages
• Multiplication Table
• Cool Maths Games
• Math Flash Cards
• Online Math Quiz
• Math Puzzles
• Binary System
• Math Dictionary
• Conversion Chart
• Homework Sheets
• Math Problem Ans
• Free Math Answers
• Printable Math Sheet
• Funny Math Answers
• Employment Test
• Math Patterns
• Link Partners
• Privacy Policy

Recent Articles

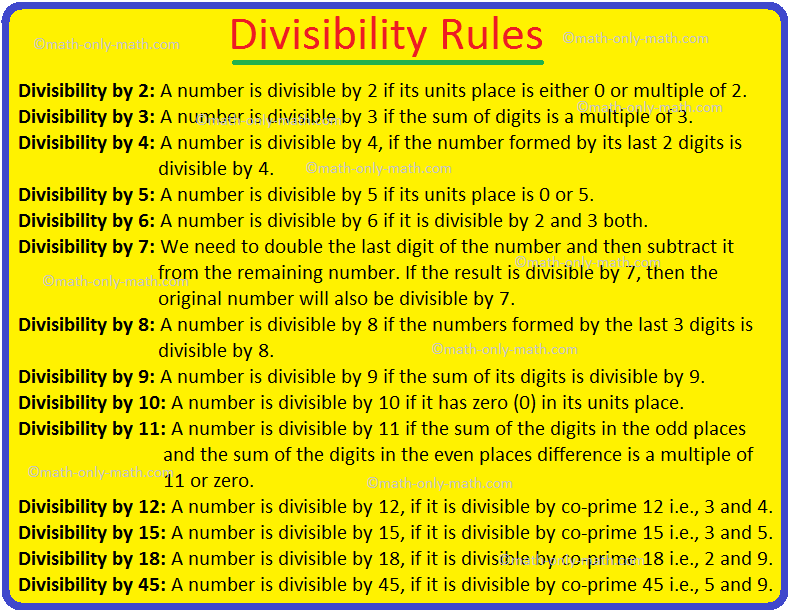
Divisibility Rules | Divisibility Test|Divisibility Rules From 2 to 18

Jun 01, 24 06:41 PM

Consecutive Numbers and Alternate Numbers | Definition | Examples

Jun 01, 24 06:20 PM

Prime and Composite Numbers | Prime Numbers | Composite Numbers

Jun 01, 24 03:45 PM

Prime Triplet Numbers | Examples on Prime Triplet | Question Answer

Jun 01, 24 11:59 AM

Perfect Numbers | Factors | Solved Examples | Sum of Its Factors |

May 31, 24 07:04 PM

© and ™ math-only-math.com. All Rights Reserved. 2010 - 2024.

CHAPTER 5: LINEAR EQUATIONS IN ONE VARIABLE

5-4: Solving Linear Equations in One Variable

Introduction.

Being able to solve linear equations in one variable is necessary to support learning of other topics in mathematics. It is also necessary to be able to transfer the skill of equation solving to other subject areas. But this can only happen if we understand the conceptual knowledge surrounding solving linear equations and don’t rely on procedural knowledge. In other words, knowing the steps required to solve linear equations is not going to get us very far. Understanding what a linear equation is telling us is the key to solving linear equations and being able to transfer our knowledge to other fields of inquiry.

  Solving Linear Equations in One Variable

To solve a linear equation in one variable, we use the properties of equality to isolate the variable on one side of the equation. That is, to end up with an equation of the form variable = number.

Explore 1 – Solving a linear equation

Before we write an equation we need to think about what makes up that equation. We need to understand the equation by asking questions: What do we know and what do we need to find? How are the known and unknown related?

Known: total cost = $250; tax rate = 6.5%  Unknown: price of the clutch; tax paid on the price of the clutch  Relationship:  The total cost of the clutch = price + tax

The maximum price Calum can afford for the clutch is $234.74.

Solving the equation is written mathematically as:

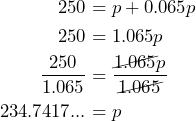
Any time a variable term has a number (coefficient) multiplied onto it, we must undo the multiplication by dividing by that number to isolate the variable (i.e., get the variable on its own).

Most linear equations cannot be solved by using only one property of equality. Most will require two or more properties of equality to be used to isolate the variable.

Explore 2 – Solving a linear equation

Dasan bought two pairs of shoes for his twins. He noticed that shipping cost $5.99 and the total cost was $93.49. Write an equation that represents this situation then solve the equation to determine the price of each pair of shoes.

Known: shipping = $5.99; total cost = for $93.49; number of pairs of shoes bought = 2.  Unknown: price of a pair of shoes

Relationship: (number of pairs of shoes) times (price of a pair of shoes) + shipping = total cost

The price of each pair of shoes was $43.75.

Applying the properties of equality results in equivalent equations that have the same solution as the original equation. These equations get simpler the closer we get to a solution. When we have a number added to a variable term, we use the subtraction property of equality to isolate the variable term. Once the variable term is isolated, we can solve for the variable by applying the division property of equality.

Explore 3 – Solving a linear equation

Uber charges a base fee of $10 per ride, then charges $1.50 per mile for each mile traveled. Jose would like to limit how much he spends on Uber to $35, how many miles can he travel?

We need to write an equation that we can solve to determine the number of miles Jose can travel.

The equation is:  total charge = base fee + mileage charge

To solve this equation we will first isolate the variable term, then isolate the variable:

Finally, we answer the question: Jose can travel 16.67 miles for $35.

Explore 4 – Variable terms on both sides

To break even means that the amount they spend to make and sell the cupcakes (the cost) equals the amount of money they will bring in from selling the cupcakes (the revenue). In other words, they will neither make a profit nor a loss.

Their cost consists of $200 for the location and $8 for every dozen cupcakes. Their revenue consists of $1.50 for each cupcake they sell.

If 12 cupcakes costs $8 to make, then each cupcake costs $8/12 = $0.67.

At the break even point, cost = revenue, with cost = $200 for the location + $0.67 times the number of cupcakes sold, and revenue = $1.50 times the number of cupcakes sold.

Now that we have solved the equation, we can answer the question: They will have to sell 241 cupcakes to break even.

To write this mathematically, each equation is equivalent to the one above it:

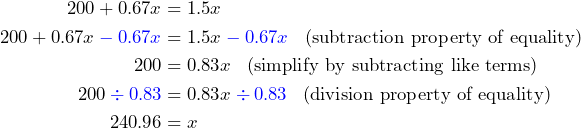
To check this for reasonability we can think of 240 cupcakes as 20 dozen cupcakes (20 · 12 = 240). And the cost of baking 20 dozen is $8 · 20 = $160. That added to the location cost of $200 = $360. On the other hand, their revenue is $1.50 per cupcake which amounts to $1.50(240) – $360. So our answer appears to make sense.

When we solve equations it is customary to write each equivalent equation directly below the equation we manipulate, with the = signs lined up. This makes it much easier to see what is happening, and to catch any errors that may occur.

Explore 5 – Variable terms on both sides

At a baseball game, Enola goes to the concession stand and buys 3 hot dogs and a $6 soda. Her friend, Malia also goes to the concession stand and buys 4 hot dogs. They are comparing the receipts and find that they both spent the same amount on their purchases. Determine the price of a hot dog.

The hot dogs cost $6 each.

Since concessions are notoriously overpriced at ball games, a $6 hot dog seems reasonable.

Solving a linear equation in one variable

• Simplify each side of the equation, if required. Use the distributive property to eliminate parentheses, and combine like terms.
• Isolate the variable term on one side of the equation and numbers on the other side. Use the addition or subtraction property of equality.
• Isolate the variable. Use the multiplication or division property of equality.
• Check your answer in the original equation to make sure it is a solution.
• Check your answer for reasonability using common sense and lived experience.

• What is the purpose of solving an equation?

The purpose of solving an equation is to determine the value of the variable that will satisfy the equation or make the equation true.

• What is a solution of an equation?

The solution of an equation is a number that will satisfy the equation or make the equation true if the value of the variable is substituted into the equation.

• Exactly how many solutions does a conditional linear equation in one variable have?
• How would we undo subtraction in an equation?

To  undo subtraction, we add the same amount to both sides of the equation.

• How would we undo multiplication in an equation?

To  undo multiplication, we divide both sides of the equation by the same amount.

Practice Exercises

• The 2021 Census counted 1.8 million Indigenous people, accounting for 5.0% of the total population in Canada [1] . Write an equation then use it to determine the population of Canada.
• 63.04 inches = 5 ft 3 in
• a) 65°F  b) 24 chirps per minute

Perspectives

• In 2021, there were 70,545 Inuit living in Canada, with 69.0% living in Inuit Nunanga t—t he homeland of Inuit in Canada. Write an equation and use it to determine how many Inuit live in Inuit Nunangat.

• The number of American military fatalities from WWI (1917-18) and WWII (1939-45) combined was less than those of the American Civil War (1861-65). 288,883 more military personnel were killed in WWII than WWI. The American Civil War accounted for 98,085 more military fatalities than WWI and WWII combined. If there were an estimated 620,000 military fatalities in the American Civil War, how many military fatalities were there in WWI and WWII?

• If 75 gallons of water are added to a pool that is already half full, the pool becomes two-thirds full. a) Define a variable and write an equation to determine the capacity of the pool.     b) Use the equation to determine the capacity of the pool.
• On the same day that Calum bought a $40,000 car, Kirsty bought a plot of land for $6000. Calum’s car is expected to lose $1450 per year, while Kirsty’s land is expected to gain $550 per year. a) Define a variable and write an equation to determine when the value of Calum’s car will equal that of Kirsty’s land.  b) Use the equation to determine when the two values will be the same.

• a) 1998     b) 2010     c) They are very close; just off my a few months. The differences can be accounted for by rounding in the model.

• a) Only 47 of the 120 answered the questions correctly.     b) 885 Americans had to take the survey to get 200 correct answers.

Solver Title

Generating PDF...

• Pre Algebra Order of Operations Factors & Primes Fractions Long Arithmetic Decimals Exponents & Radicals Ratios & Proportions Percent Modulo Number Line Expanded Form Mean, Median & Mode
• Algebra Equations Inequalities System of Equations System of Inequalities Basic Operations Algebraic Properties Partial Fractions Polynomials Rational Expressions Sequences Power Sums Interval Notation Pi (Product) Notation Induction Logical Sets Word Problems
• Pre Calculus Equations Inequalities Scientific Calculator Scientific Notation Arithmetics Complex Numbers Polar/Cartesian Simultaneous Equations System of Inequalities Polynomials Rationales Functions Arithmetic & Comp. Coordinate Geometry Plane Geometry Solid Geometry Conic Sections Trigonometry
• Calculus Derivatives Derivative Applications Limits Integrals Integral Applications Integral Approximation Series ODE Multivariable Calculus Laplace Transform Taylor/Maclaurin Series Fourier Series Fourier Transform
• Functions Line Equations Functions Arithmetic & Comp. Conic Sections Transformation
• Linear Algebra Matrices Vectors
• Trigonometry Identities Proving Identities Trig Equations Trig Inequalities Evaluate Functions Simplify
• Statistics Mean Geometric Mean Quadratic Mean Average Median Mode Order Minimum Maximum Probability Mid-Range Range Standard Deviation Variance Lower Quartile Upper Quartile Interquartile Range Midhinge Standard Normal Distribution
• Physics Mechanics
• Chemistry Chemical Reactions Chemical Properties
• Finance Simple Interest Compound Interest Present Value Future Value
• Economics Point of Diminishing Return
• Conversions Roman Numerals Radical to Exponent Exponent to Radical To Fraction To Decimal To Mixed Number To Improper Fraction Radians to Degrees Degrees to Radians Hexadecimal Scientific Notation Distance Weight Time Volume
• Pre Algebra
• One-Step Addition
• One-Step Subtraction
• One-Step Multiplication
• One-Step Division
• One-Step Decimals
• Two-Step Integers
• Two-Step Add/Subtract
• Two-Step Multiply/Divide
• Two-Step Fractions
• Two-Step Decimals
• Multi-Step Integers
• Multi-Step with Parentheses
• Multi-Step Rational
• Multi-Step Fractions
• Multi-Step Decimals
• Solve by Factoring
• Completing the Square
• Quadratic Formula
• Biquadratic
• Logarithmic
• Exponential
• Rational Roots
• Floor/Ceiling
• Equation Given Roots
• Newton Raphson
• Substitution
• Elimination
• Cramer's Rule
• Gaussian Elimination
• System of Inequalities
• Perfect Squares
• Difference of Squares
• Difference of Cubes
• Sum of Cubes
• Polynomials
• Distributive Property
• FOIL method
• Perfect Cubes
• Binomial Expansion
• Negative Rule
• Product Rule
• Quotient Rule
• Expand Power Rule
• Fraction Exponent
• Exponent Rules
• Exponential Form
• Logarithmic Form
• Absolute Value
• Rational Number
• Powers of i
• Complex Form
• Partial Fractions
• Is Polynomial
• Leading Coefficient
• Leading Term
• Standard Form
• Complete the Square
• Synthetic Division
• Linear Factors
• Rationalize Denominator
• Rationalize Numerator
• Identify Type
• Convergence
• Interval Notation
• Pi (Product) Notation
• Boolean Algebra
• Truth Table
• Mutual Exclusive
• Cardinality
• Caretesian Product
• Age Problems
• Distance Problems
• Cost Problems
• Investment Problems
• Number Problems
• Percent Problems
• Addition/Subtraction
• Multiplication/Division
• Dice Problems
• Coin Problems
• Card Problems
• Pre Calculus
• Linear Algebra
• Trigonometry
• Conversions

Most Used Actions

Number line.

• \frac{3}{4}x+\frac{5}{6}=5x-\frac{125}{3}
• \sqrt{2}x-\sqrt{3}=\sqrt{5}
• 7y+5-3y+1=2y+2
• \frac{x}{3}+\frac{x}{2}=10
• What is a linear equation?
• A linear equation represents a straight line on a coordinate plane. It can be written in the form: y = mx + b where m is the slope of the line and b is the y-intercept.
• How do you find the linear equation?
• To find the linear equation you need to know the slope and the y-intercept of the line. To find the slope use the formula m = (y2 - y1) / (x2 - x1) where (x1, y1) and (x2, y2) are two points on the line. The y-intercept is the point at which x=0.
• What are the 4 methods of solving linear equations?
• There are four common methods to solve a system of linear equations: Graphing, Substitution, Elimination and Matrix.
• How do you identify a linear equation?
• Here are a few ways to identify a linear equation: Look at the degree of the equation, a linear equation is a first-degree equation. Check if the equation has two variables. Graph the equation.
• What is the most basic linear equation?
• The most basic linear equation is a first-degree equation with one variable, usually written in the form of y = mx + b, where m is the slope of the line and b is the y-intercept.

linear-equation-calculator

• Middle School Math Solutions – Equation Calculator Welcome to our new "Getting Started" math solutions series. Over the next few weeks, we'll be showing how Symbolab...

Please add a message.

Message received. Thanks for the feedback.

If you're seeing this message, it means we're having trouble loading external resources on our website.

If you're behind a web filter, please make sure that the domains *.kastatic.org and *.kasandbox.org are unblocked.

To log in and use all the features of Khan Academy, please enable JavaScript in your browser.

Unit 2: Linear equations in one variable

Solving equations with variable on one side.

• Worked example: two-step equations (Opens a modal)
• Equation with variables on both sides: fractions (Opens a modal)
• Two-step equations Get 5 of 7 questions to level up!
• Equations with variables on both sides: decimals & fractions Get 3 of 4 questions to level up!

Solving equations with variables on both sides

• Equations with parentheses (Opens a modal)
• Equations with variables on both sides Get 3 of 4 questions to level up!
• Equations with parentheses: decimals & fractions Get 3 of 4 questions to level up!

Equations reducible to linear form

• No videos or articles available in this lesson
• Solving equations reducible to linear form Get 3 of 4 questions to level up!

Linear equations word problems

• Two-step equation word problem: garden (Opens a modal)
• Sums of consecutive integers (Opens a modal)
• Two-step equation word problem: oranges (Opens a modal)
• Word problems linear equations (basic) Get 3 of 4 questions to level up!
• Sums of consecutive integers Get 3 of 4 questions to level up!
• Linear equations word problems (advanced) Get 3 of 4 questions to level up!

Our mission is to provide a free, world-class education to anyone, anywhere.

Khan Academy is a 501(c)(3) nonprofit organization. Donate or volunteer today!

Site Navigation

• Our interns
• Our content specialists
• Our leadership
• Our supporters
• Our contributors
• Our finances
• Internships
• Help center
• Support community
• Share your story

Download our apps

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons

Margin Size

• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

2.1: Linear Equations

• Last updated
• Save as PDF
• Page ID 96380

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)

( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

\( \newcommand{\Span}{\mathrm{span}}\)

\( \newcommand{\id}{\mathrm{id}}\)

\( \newcommand{\kernel}{\mathrm{null}\,}\)

\( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\)

\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\)

\( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)

\( \newcommand{\vectorA}[1]{\vec{#1}}      % arrow\)

\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}}      % arrow\)

\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vectorC}[1]{\textbf{#1}} \)

\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)

\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)

\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)

Learning Objectives

By the end of this section, you will be able to:

• Understand what it means to solve a linear equation.
• Solve linear equations with one unknown, i.e., one-variable.

Be Prepared

Before you get started, take this readiness quiz.

• Simplify \(3(2+x)\).
• Simplify \(\dfrac{1}{3}+\dfrac{9}{4}\cdot \dfrac{5}{7}\).
• Is the expression \(9 x^{2}-12 x+4\) linear?

Introduction to Equations

In this unit we will use these expressions in applications!In the previous unit we used expressions to represent quantities when it involved a quantity that is either unknown or could be any of a number of values. For example, we may want to represent the total amount of money in a bin that had 5 dollars and a certain number of quarters. How could we do this? We first did some examples where we chose a specific number of quarters:

If we had 3 quarters then we have \(\$ 5.75\). If the bin contains 7 quarters then the bin has \(\$ 5+1.75=\$ 6.75\). Using this as an example, we can try to discover what we do if we don't know how many quarters we are dealing with. We let the variable \(q\) represent the number of quarters. Then we can translate the sum made by having \(q\) quarters: \(\dfrac{q}{4}\). We can test this on our 7 quarters: \(\dfrac{7}{4}=1.75\). To then find the total in the bin we add the 5 dollars. So the total amount in the bin is \(5+q/4.\)

We can test this on 3 quarters:

\[5+\dfrac{3}{4}=5.75\]

and on 7 quarters:

\[5+\dfrac{7}{4}=5+1.75=6.75.\]

But in this unit, we recognize this expression represents the amount of money in the bin no matter what \(q\) is and we use this fact to solve problems. For example, suppose we know that the money in the bin is equal to \(\$8.25\) and we want to know how many quarters there are. Then we represent the amount of money in the bin in two ways which then must be equal (since they represent the same quantity):

\(8.25=5+\dfrac{q}{4}.\)

This is an assertion about \(q\). Sometimes we have used equal signs during a simplification of an expression. Such equal signs implicitly mean that equation holds for all values of the variables except those that leave an expression undefined. In the case of this equation and others in this unit, these equalities say something about the variable, and for 'most' values of the variable the equation is false. We will seek the values which make the equality true, .i.e., we seek to solve these equations.

We can imagine ourselves looking at this bin and putting aside the \(\$5\). We then know that what is left is both \(3.25\) and \(\dfrac{q}{4}\), so that the contribution of the quarters is \(\$3.25\) which we can figure out using our experience with counting money that there are \(13\) quarters.

The expression \(5+\dfrac{q}{4}\) has two basic interpretations: If there are several such bins then we could use the expression \(5+\dfrac{q}{4}\) and substitute the number of quarters, one at a time, in for \(q\) to find the total amount of money in each bin; or maybe, for example we have only one bin but someone will tell us later how many quarters are in the bin and we will use this expression, substituting what they tell us for \(q\), to find out how much money is in that bin. The latter interpretation is what was used above. We know there were a certain but currently unknown number of quarters in the bin. Combining this with the information that the total amount of money in the bin was \(\$8.25\) we learned what \(q\) must be.

The above is just a simple example to illustrate the basic notions we will be using in this section. We will do many examples with the expressions we used in the last unit. Before continuing, make sure you understand this most simple example.

Linear Equations and Their Solutions

Just as linear expressions are the simplest expressions involving only multiplication and addition of numbers, here we consider equations involving these expressions.

We begin by returning to the example in the introduction and considering the 'solution.'

You may be familiar with how to solve this equation, but the basics of solving equations lie in this one example.

Recall that in the example we had a bin with 5 dollars and a certain number of quarters. We arrived at an expression equal to the amount of money in the bin once the number of quarters (which we will call '\(q\)') is known and substituted. The expression is

\(5+\dfrac{q}{4}.\)

The question raised in the introduction was to suppose we know something about the amount of money in the bin, namely, that it contains \(\$8.25\) and we want to find the number of quarters. We wrote the amount of money in two ways (which then must be equal!). On the one hand we know the bin contains \(\$8.25\) and on the other hand we know that if it has \(q\) quarters, it has \(5+\dfrac{q}{4}.\) dollars. So,

We figured out how many quarters there are (13) using our heads and experience. Here, we would like to proceed differently so that it sets the stage for more complicated problems.

The equality \(8.25=5+\dfrac{q}{4}.\) means that if we substitute the number of quarters in for the variable \(q\), we have a true statement. We already saw that there are 13 quarters and we see that

We say that \(8.25=5+\dfrac{q}{4}\) is an equation with one variable and \(q=13\) is a solution. This equation is in fact a linear equation since the expressions on both sides are linear expressions.

This is a verification of the solution. If we were unable to figure this out by using our experience, how could we find the solution?

Notice that we are interested in finding \(q\). If we knew what \(q\) was we could evaluate \(q\) by first dividing by 4 and then adding the result to 5. Here we must use the order of operations. So to undo these actions, we must undo them in the opposite order. And to maintain the truth of the equation, we must do the same thing to both sides.

Note that if you do the arithmetic correctly you should see the operation you are undoing disappearing as you wished!

We have had extensive practice with simplifications in the first unit, so from now on we will just indicate when we have simplified.

We introduce some general vocabulary:

An equation is   a mathematical sentence of the form (an expression)\(=\) (another expression).

A solution to an equation in a variable (lets call it \(x\)) is a number that we can substitute in for \(x\) that makes the equation true.

Two equations are equivalent if they have the same solutions.

Finding the solutions of an equation is called solving the equation.

A linear equation with one variable \(x\) is an equation that is equivalent to an equation \(Ax+B=0\), where \(A\not= 0\).

To solve a linear equation with one variable means to find the number that when substituted makes the equation true. If \(a\) is a solution to the equation with the variable \(x\), then we may also say \(x=a\), is a solution (it is a simplification of the original assertion).

Example \(\PageIndex{4}\)

Why is the equation \(5=3x-2\) linear? Solve the equation.

The equation is linear because both sides can be written in the form \(ax+b\) and so are linear expressions. We note that for most values of \(x\) the equation is not satisfied.

What is the solution then? Or maybe there is more than one?

The assertion about \(x\) is that if we multiply by 3 and then subtract 2 from the result, we should get 5. We need to undo this in the reverse order. And, to preserve the equality, whatever we do to one side of the equal sign we must do to the other. We need to write an equivalent equation of the form \(x=a\), that is, to see to it that \(x\) is on one side of an equation and a number is on the other side.

We see that by undoing the actions on \(x\), we were led to the conclusion that \(x\) must be 7/3. So there is only one solution!

Try It \(\PageIndex{5}\)

Why is the equation \(2x+5=3\) linear? Solve the equation.

Answers vary. \(x=-1\)

Try It \(\PageIndex{6}\)

Why is the equation \(2m+5=-m+3\) linear? Solve the equation. Note that you can do anything to both sides of the equation to get your desired outcome!

Answers vary. \(m=-2/3 \)

Example \(\PageIndex{7}\)

The perimeter of an enclosed rectangle is 60 feet. The length is twice six more than the width. What are the dimensions of the enclosure?

Let's start with some example to understand the relation between the width and the length. If the width is 4 feet, for example, and the length is twice (six more than the width), then the length is 2 times 10 feet or, 20 feet. Since this leads to a perimeter of 20+4+20+4=48 feet (which isn't the correct perimeter, but has the correct width/length relation). We see here also that our answer should have a width larger than 4 feet since the perimeter of 48 feet is less than the required 60 feet. If the width is 10 feet, then the length is twice (six more than the width), or twice 16 feet, or, 32 feet. The perimeter in this example will be greater than 64 so the width here is too long. But we can use our examples to lead us to write down an expression for the length if \(w\) stands for the unknown width. The length is twice (six more than the width), or twice (6+\(w\)). Now we can't actually add since we don't know what \(w\) is, but we can still multiply by 2 to get that the length is \(2(6+w)\).  We indicate this on a picture.  This picture is only to help us with relationships and will very likely not have the final length or width correct!

So, we know then that the perimeter for the width \(w\) we are looking for is

\(w+2(6+w)+w+2(6+w)=2w+4(6+w).\)

We know that the perimeter is also 60 feet, so 60 must be equal to the expression above for the \(w\) we seek:

\(60= 2w+4(6+w).\)

We can use our skills of simplifying to rewrite the right side to get the equivalent equation

Notice that the right hand side says to multiply \(w\) by 6 and then add 24. To undo these actions we must undo them in the opposite order!

Now, the two sides of this equation are equal for the \(w\) we are looking for, so the equality is preserved if we subtract 24 from both sides.

This gives us:

\(60-24= 6w+24-24\), or, simplifying both sides, \(36= 6w.\)

We can then divide both sides by 6 and since 36 is the same as \(6w\) for the \(w\) we are looking for, dividing both sides by 6 will result in an equality:

\(36/6= 6w/6\), or, \(w=6 \;\mathrm{feet}\).

We recall that the length is \(2(6+w)=2(6+6)=24\) feet.

So the rectangular enclosure has a width of 6 feet and a length of 24 feet.

(We can check that the length is twice six more than the width and that the perimeter is 60 feet).

Try It \(\PageIndex{8}\)

The perimeter of an enclosed isosceles triangle is 40 feet. The length of the shortest side is 7 less than half of the two longest (equal) sides. What are the length of the sides of the enclosure? Give some examples of any expression you develop and write your solution in detail.

Answers vary. \(94/5\; \mathrm{ft}, 94/5 \;\mathrm{ft}, 12/5\; \mathrm{ ft} .\)

Writing Exercises \(\PageIndex{9}\)

• How do you recognize a linear equation?
• Give an example of a linear equation.
• Do all linear equations have a solution?
• Explain the relationship between the order of operations and the process of solving \(3x-4=7\).

Exit Problem

A rectangular garden has a length the is 10 feet longer than its width.  The perimeter is 42 feet.  What are the dimensions of the garden?

Key Concepts

Linear equation

Solution to a linear equation

Solving a linear equation

Game Central

Similar problems from web search.

• Trending Now
• Foundational Courses
• Data Science
• Practice Problem
• Machine Learning
• System Design
• DevOps Tutorial
• Interview Preparation For Software Developers
• Must Coding Questions - Company-wise
• Must Do Coding Questions - Topic-wise
• Company-wise Practice Problems
• Company Preparation
• Competitive Programming
• Software Design-Patterns
• Company-wise Interview Experience
• Experienced - Interview Experiences
• Internship - Interview Experiences
• Problem of the Day
• Topic-wise Practice
• Difficulty Level - School
• Difficulty Level - Basic
• Difficulty Level - Easy
• Difficulty Level - Medium
• Difficulty Level - Hard
• Leaderboard !!
• Explore More...
• Linked List
• Binary Tree
• Binary Search Tree
• Advance Data Structures
• All Data Structures
• Analysis of Algorithms
• Searching Algorithms
• Sorting Algorithms
• Pattern Searching
• Geometric Algorithms
• Mathematical Algorithms
• Randomized Algorithms
• Greedy Algorithms
• Dynamic Programming
• Divide & Conquer
• Backtracking
• Branch & Bound
• All Algorithms
• Tailwind CSS
• Web Browser
• File Formats
• Operating Systems
• Computer Network
• Computer Organization & Architecture
• Compiler Design
• Digital Elec. & Logic Design
• Software Engineering
• Engineering Mathematics
• Complete Data Science Course
• Data Science Tutorial
• Machine Learning Tutorial
• Deep Learning Tutorial
• NLP Tutorial
• Machine Learning Projects
• Data Analysis Tutorial
• Python Tutorial
• Django Tutorial
• Pandas Tutorial
• Kivy Tutorial
• Tkinter Tutorial
• OpenCV Tutorial
• Selenium Tutorial
• GATE CS Notes
• Gate Corner
• Previous Year GATE Papers
• Last Minute Notes (LMNs)
• Important Topic For GATE CS
• GATE Course
• Previous Year Paper: CS exams
• Git Tutorial
• AWS Tutorial
• Docker Tutorial
• Kubernetes Tutorial
• Microsoft Azure Tutorial
• Python Quiz
• JavaScript Quiz
• Data Structures Quiz
• Algorithms Quiz
• Topic-wise MCQs
• CBSE Notes 2023-24
• CBSE Class 8 Notes
• CBSE Class 9 Notes
• CBSE Class 10 Notes
• CBSE Class 11 Notes
• CBSE Class 12 Notes
• School Programming
• English Grammar
• Accountancy
• Business Studies
• Human Resource Management
• Top 100 Puzzles
• Mathematical Riddles

Solving for One Variable

Solve for 𝑦 in the equation 2𝑥+𝑦=7 when 𝑥=2.

This question is part of this quiz :

Please comment below if you find anything wrong in the above post Feeling lost in the world of random DSA topics, wasting time without progress? It's time for a change! Join our DSA course, where we'll guide you on an exciting journey to master DSA efficiently and on schedule. Ready to dive in? Explore our Free Demo Content and join our DSA course, trusted by over 100,000 geeks!

• DSA In JAVA/C++
• DSA in Python
• DSA in JavaScript