different methods of solving assignment problem

Assignment Problem: Meaning, Methods and Variations | Operations Research

After reading this article you will learn about:- 1. Meaning of Assignment Problem 2. Definition of Assignment Problem 3. Mathematical Formulation 4. Hungarian Method 5. Variations.

Meaning of Assignment Problem:

An assignment problem is a particular case of transportation problem where the objective is to assign a number of resources to an equal number of activities so as to minimise total cost or maximize total profit of allocation.

The problem of assignment arises because available resources such as men, machines etc. have varying degrees of efficiency for performing different activities, therefore, cost, profit or loss of performing the different activities is different.

Thus, the problem is “How should the assignments be made so as to optimize the given objective”. Some of the problem where the assignment technique may be useful are assignment of workers to machines, salesman to different sales areas.

Definition of Assignment Problem:

ADVERTISEMENTS:

Suppose there are n jobs to be performed and n persons are available for doing these jobs. Assume that each person can do each job at a term, though with varying degree of efficiency, let c ij be the cost if the i-th person is assigned to the j-th job. The problem is to find an assignment (which job should be assigned to which person one on-one basis) So that the total cost of performing all jobs is minimum, problem of this kind are known as assignment problem.

The assignment problem can be stated in the form of n x n cost matrix C real members as given in the following table:

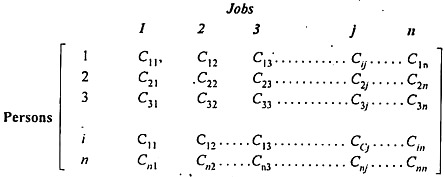
www.springer.com The European Mathematical Society

StatProb Collection
Recent changes
Current events
Random page
Project talk
Request account
What links here
Related changes
Special pages
Printable version
Permanent link
Page information
View source

Assignment problem

The problem of optimally assigning $ m $ individuals to $ m $ jobs. It can be formulated as a linear programming problem that is a special case of the transport problem :

maximize $ \sum _ {i,j } c _ {ij } x _ {ij } $

$$ \sum _ { j } x _ {ij } = a _ {i} , i = 1 \dots m $$

(origins or supply),

$$ \sum _ { i } x _ {ij } = b _ {j} , j = 1 \dots n $$

(destinations or demand), where $ x _ {ij } \geq 0 $ and $ \sum a _ {i} = \sum b _ {j} $, which is called the balance condition. The assignment problem arises when $ m = n $ and all $ a _ {i} $ and $ b _ {j} $ are $ 1 $.

If all $ a _ {i} $ and $ b _ {j} $ in the transposed problem are integers, then there is an optimal solution for which all $ x _ {ij } $ are integers (Dantzig's theorem on integral solutions of the transport problem).

In the assignment problem, for such a solution $ x _ {ij } $ is either zero or one; $ x _ {ij } = 1 $ means that person $ i $ is assigned to job $ j $; the weight $ c _ {ij } $ is the utility of person $ i $ assigned to job $ j $.

The special structure of the transport problem and the assignment problem makes it possible to use algorithms that are more efficient than the simplex method . Some of these use the Hungarian method (see, e.g., [a5] , [a1] , Chapt. 7), which is based on the König–Egervary theorem (see König theorem ), the method of potentials (see [a1] , [a2] ), the out-of-kilter algorithm (see, e.g., [a3] ) or the transportation simplex method.

In turn, the transportation problem is a special case of the network optimization problem.

A totally different assignment problem is the pole assignment problem in control theory.

This page was last edited on 5 April 2020, at 18:48.
Privacy policy
About Encyclopedia of Mathematics
Disclaimers
Impressum-Legal

404 Not found

Operations Research by

Get full access to Operations Research and 60K+ other titles, with a free 10-day trial of O'Reilly.

There are also live events, courses curated by job role, and more.

Assignment Problem

5.1 introduction.

The assignment problem is one of the special type of transportation problem for which more efficient (less-time consuming) solution method has been devised by KUHN (1956) and FLOOD (1956). The justification of the steps leading to the solution is based on theorems proved by Hungarian mathematicians KONEIG (1950) and EGERVARY (1953), hence the method is named Hungarian.

5.2 GENERAL MODEL OF THE ASSIGNMENT PROBLEM

Consider n jobs and n persons. Assume that each job can be done only by one person and the time a person required for completing the i th job (i = 1,2,...n) by the j th person (j = 1,2,...n) is denoted by a real number C ij . On the whole this model deals with the assignment of n candidates to n jobs ...

Get Operations Research now with the O’Reilly learning platform.

O’Reilly members experience books, live events, courses curated by job role, and more from O’Reilly and nearly 200 top publishers.

Don’t leave empty-handed

Get Mark Richards’s Software Architecture Patterns ebook to better understand how to design components—and how they should interact.

It’s yours, free.

Check it out now on O’Reilly

Dive in for free with a 10-day trial of the O’Reilly learning platform—then explore all the other resources our members count on to build skills and solve problems every day.

Google OR-Tools
Español – América Latina
Português – Brasil
Tiếng Việt

Solving an Assignment Problem

This section presents an example that shows how to solve an assignment problem using both the MIP solver and the CP-SAT solver.

In the example there are five workers (numbered 0-4) and four tasks (numbered 0-3). Note that there is one more worker than in the example in the Overview .

The costs of assigning workers to tasks are shown in the following table.

The problem is to assign each worker to at most one task, with no two workers performing the same task, while minimizing the total cost. Since there are more workers than tasks, one worker will not be assigned a task.

MIP solution

The following sections describe how to solve the problem using the MPSolver wrapper .

Import the libraries

The following code imports the required libraries.

Create the data

The following code creates the data for the problem.

The costs array corresponds to the table of costs for assigning workers to tasks, shown above.

Declare the MIP solver

The following code declares the MIP solver.

Create the variables

The following code creates binary integer variables for the problem.

Create the constraints

Create the objective function.

The following code creates the objective function for the problem.

The value of the objective function is the total cost over all variables that are assigned the value 1 by the solver.

Invoke the solver

The following code invokes the solver.

Print the solution

The following code prints the solution to the problem.

Here is the output of the program.

Complete programs

Here are the complete programs for the MIP solution.

CP SAT solution

The following sections describe how to solve the problem using the CP-SAT solver.

Declare the model

The following code declares the CP-SAT model.

The following code sets up the data for the problem.

The following code creates the constraints for the problem.

Here are the complete programs for the CP-SAT solution.

Except as otherwise noted, the content of this page is licensed under the Creative Commons Attribution 4.0 License , and code samples are licensed under the Apache 2.0 License . For details, see the Google Developers Site Policies . Java is a registered trademark of Oracle and/or its affiliates.

Last updated 2023-01-02 UTC.

Principedia

Successful Strategies for Solving Problems on Assignments

Solving complex problems is a challenging task and warrants ongoing effort throughout your career. A number of approaches that expert problem-solvers find useful are summarized below, and you may find these strategies helpful in your own work. Any quantitative problem, whether in economics, science, or engineering, requires a two-step approach: analyze, then compute. Jumping directly to “number-crunching” without thinking through the logic of the problem is counter-productive. Conversely, analyzing a problem and then computing carelessly  will not result in the right answer either. So, think first, calculate, and always check your results. And remember, attitude matters. Approach solving a problem as something that you know you can do, rather than something you think that you can’t do. Very few of us can see the answer to a problem without working through various approaches first.

Analysis Stage

Read the problem carefully at least twice, aloud if possible, then restate the problem in your own words.
Write down all the information that you know in the problem and separate, if necessary, the “givens” from the “constraints.”
Think about what can be done with the information that is given. What are some relationships within the information given? What does this particular problem have in common conceptually with course material or other questions that you have solved?
Draw pictures or graphs to help you sort through what’s really going on in the problem. These will help you recall related course material that will help you solve the problem. However, be sure to check that the assumptions underlying the picture or graph you have drawn are the same as the assumptions made in the problem. If they are not, you will need to take this into consideration when setting up your approach.

Computing Stage

If the actual numbers involved in the problem are too large, small, or abstract and seem to be getting in the way of your thinking, substitute simple numbers and plan your approach. Then, once you get an understanding of the concepts in the problem, you can go back to the numbers given.
Once you have a plan, do the necessary calculations. If you think of a simpler or more elegant approach, you can try it afterwards and use it as a check of your logic. Be careful about changing your approach in the middle of a problem. You can inadvertently include some incorrect or inapplicable assumptions from the prior plan.
Throughout the computing stage, pause periodically to be sure that you understand the intuition behind each concept in the problem. Doing this will not only strengthen your understanding of the material, but it will also help you in solving other problems that also focus on those concepts.
Resist the temptation to consult the answer key before you have finished the problem. Problems often look logical when someone else does them; that recognition does not require the same knowledge as solving the problem yourself. Likewise, when soliciting help from the AI or course head, ask for direction or a helpful tip only—avoid having them work the problem for you. This approach will help ensure that you really understand the problem—an essential prerequisite for successfully solving problems on exams and quizzes where no outside help is available.
Check your results. Does the answer make sense given the information you have and the concepts involved? Does the answer make sense in the real world? Are the units reasonable? Are the units the ones specified in the problem? If you substitute your answer for the unknown in the problem, does it fit the criteria given? Does your answer fit within the range of an estimate that you made prior to calculating the result? One especially effective way to check your results is to work with a study partner or group. Discussing various options for a problem can help you uncover both computational errors and errors in your thinking about the problem. Before doing this, of course, make sure that working with someone else is acceptable to your course instructor.
Ask yourself why this question is important. Lectures, precepts, problem sets, and exams are all intended to increase your knowledge of the subject. Thinking about the connection between a problem and the rest of the course material will strengthen your overall understanding.

If you get stuck, take a break. Research has shown that the brain works very productively on problems while we sleep—so plan your problem-solving sessions in such a way that you do a “first pass.” Then, get a night’s rest, return to the problem set the next day, and think about approaching the problem in an entirely different way.

References and Further Reading:

Adapted in part from Walter Pauk. How to Study in College , 7th edition, Houghton Mifflin Co., 2001

← Questions to Ask Yourself When Problem Solving
Breaking Down Large Projects Into Manageable Pieces →

Procedure, Example Solved Problem | Operations Research - Solution of assignment problems (Hungarian Method) | 12th Business Maths and Statistics : Chapter 10 : Operations Research

Chapter: 12th business maths and statistics : chapter 10 : operations research.

Solution of assignment problems (Hungarian Method)

First check whether the number of rows is equal to the numbers of columns, if it is so, the assignment problem is said to be balanced.

Step :1 Choose the least element in each row and subtract it from all the elements of that row.

Step :2 Choose the least element in each column and subtract it from all the elements of that column. Step 2 has to be performed from the table obtained in step 1.

Step:3 Check whether there is atleast one zero in each row and each column and make an assignment as follows.

Step :4 If each row and each column contains exactly one assignment, then the solution is optimal.

Example 10.7

Solve the following assignment problem. Cell values represent cost of assigning job A, B, C and D to the machines I, II, III and IV.

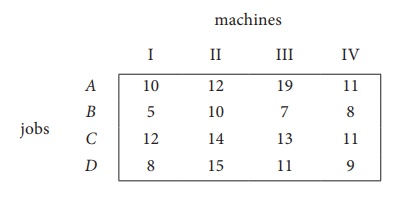
Here the number of rows and columns are equal.

∴ The given assignment problem is balanced. Now let us find the solution.

Step 1: Select a smallest element in each row and subtract this from all the elements in its row.

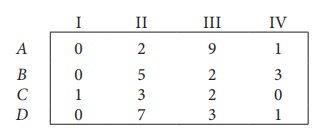
Look for atleast one zero in each row and each column.Otherwise go to step 2.

Step 2: Select the smallest element in each column and subtract this from all the elements in its column.

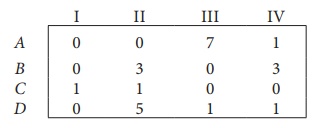
Since each row and column contains atleast one zero, assignments can be made.

Step 3 (Assignment):

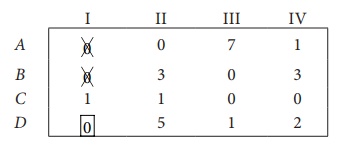
Thus all the four assignments have been made. The optimal assignment schedule and total cost is

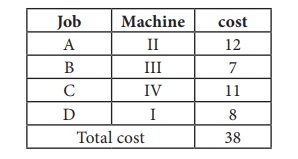
The optimal assignment (minimum) cost

Example 10.8

Consider the problem of assigning five jobs to five persons. The assignment costs are given as follows. Determine the optimum assignment schedule.

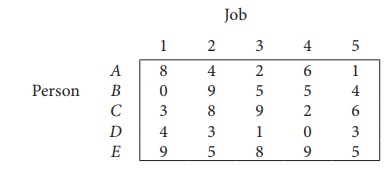
∴ The given assignment problem is balanced.

Now let us find the solution.

The cost matrix of the given assignment problem is

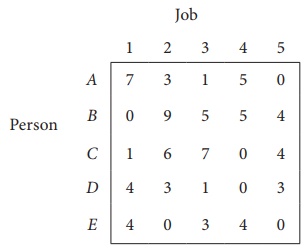
Column 3 contains no zero. Go to Step 2.

Thus all the five assignments have been made. The Optimal assignment schedule and total cost is

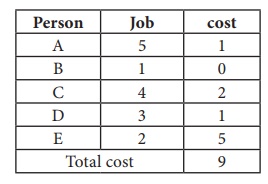
The optimal assignment (minimum) cost = ` 9

Example 10.9

Solve the following assignment problem.

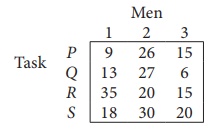
Since the number of columns is less than the number of rows, given assignment problem is unbalanced one. To balance it , introduce a dummy column with all the entries zero. The revised assignment problem is

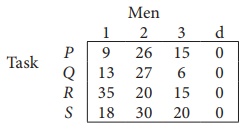
Here only 3 tasks can be assigned to 3 men.

Step 1: is not necessary, since each row contains zero entry. Go to Step 2.

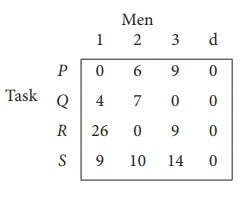
Step 3 (Assignment) :

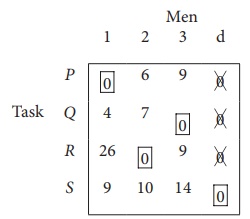
Since each row and each columncontains exactly one assignment,all the three men have been assigned a task. But task S is not assigned to any Man. The optimal assignment schedule and total cost is

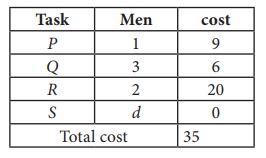
The optimal assignment (minimum) cost = ₹ 35

Assignment Problem: Linear Programming

The assignment problem is a special type of transportation problem , where the objective is to minimize the cost or time of completing a number of jobs by a number of persons.

In other words, when the problem involves the allocation of n different facilities to n different tasks, it is often termed as an assignment problem.

The model's primary usefulness is for planning. The assignment problem also encompasses an important sub-class of so-called shortest- (or longest-) route models. The assignment model is useful in solving problems such as, assignment of machines to jobs, assignment of salesmen to sales territories, travelling salesman problem, etc.

It may be noted that with n facilities and n jobs, there are n! possible assignments. One way of finding an optimal assignment is to write all the n! possible arrangements, evaluate their total cost, and select the assignment with minimum cost. But, due to heavy computational burden this method is not suitable. This chapter concentrates on an efficient method for solving assignment problems that was developed by a Hungarian mathematician D.Konig.

"A mathematician is a device for turning coffee into theorems." -Paul Erdos

Formulation of an assignment problem

Suppose a company has n persons of different capacities available for performing each different job in the concern, and there are the same number of jobs of different types. One person can be given one and only one job. The objective of this assignment problem is to assign n persons to n jobs, so as to minimize the total assignment cost. The cost matrix for this problem is given below:

The structure of an assignment problem is identical to that of a transportation problem.

To formulate the assignment problem in mathematical programming terms , we define the activity variables as

for i = 1, 2, ..., n and j = 1, 2, ..., n

In the above table, c ij is the cost of performing jth job by ith worker.

Generalized Form of an Assignment Problem

The optimization model is

Minimize c 11 x 11 + c 12 x 12 + ------- + c nn x nn

subject to x i1 + x i2 +..........+ x in = 1 i = 1, 2,......., n x 1j + x 2j +..........+ x nj = 1 j = 1, 2,......., n

x ij = 0 or 1

In Σ Sigma notation

x ij = 0 or 1 for all i and j

An assignment problem can be solved by transportation methods, but due to high degree of degeneracy the usual computational techniques of a transportation problem become very inefficient. Therefore, a special method is available for solving such type of problems in a more efficient way.

Assumptions in Assignment Problem

Number of jobs is equal to the number of machines or persons.
Each man or machine is assigned only one job.
Each man or machine is independently capable of handling any job to be done.
Assigning criteria is clearly specified (minimizing cost or maximizing profit).

Share this article with your friends

Operations Research Simplified Back Next

Goal programming Linear programming Simplex Method Transportation Problem

35 problem-solving techniques and methods for solving complex problems

Design your next session with SessionLab

Join the 150,000+ facilitators  using SessionLab.

How do you identify problems?

How do you identify the right solution.

Tips for more effective problem-solving

Complete problem-solving methods

Problem-solving techniques to identify and analyze problems
Problem-solving techniques for developing solutions

Problem-solving warm-up activities

Closing activities for a problem-solving process.

Before you can move towards finding the right solution for a given problem, you first need to identify and define the problem you wish to solve.

Here, you want to clearly articulate what the problem is and allow your group to do the same. Remember that everyone in a group is likely to have differing perspectives and alignment is necessary in order to help the group move forward.

Identifying a problem accurately also requires that all members of a group are able to contribute their views in an open and safe manner. It can be scary for people to stand up and contribute, especially if the problems or challenges are emotive or personal in nature. Be sure to try and create a psychologically safe space for these kinds of discussions.

Remember that problem analysis and further discussion are also important. Not taking the time to fully analyze and discuss a challenge can result in the development of solutions that are not fit for purpose or do not address the underlying issue.

Successfully identifying and then analyzing a problem means facilitating a group through activities designed to help them clearly and honestly articulate their thoughts and produce usable insight.

With this data, you might then produce a problem statement that clearly describes the problem you wish to be addressed and also state the goal of any process you undertake to tackle this issue.

Finding solutions is the end goal of any process. Complex organizational challenges can only be solved with an appropriate solution but discovering them requires using the right problem-solving tool.

After you’ve explored a problem and discussed ideas, you need to help a team discuss and choose the right solution. Consensus tools and methods such as those below help a group explore possible solutions before then voting for the best. They’re a great way to tap into the collective intelligence of the group for great results!

Remember that the process is often iterative. Great problem solvers often roadtest a viable solution in a measured way to see what works too. While you might not get the right solution on your first try, the methods below help teams land on the most likely to succeed solution while also holding space for improvement.

Every effective problem solving process begins with an agenda . A well-structured workshop is one of the best methods for successfully guiding a group from exploring a problem to implementing a solution.

In SessionLab, it’s easy to go from an idea to a complete agenda . Start by dragging and dropping your core problem solving activities into place . Add timings, breaks and necessary materials before sharing your agenda with your colleagues.

The resulting agenda will be your guide to an effective and productive problem solving session that will also help you stay organized on the day!

Tips for more effective problem solving

Problem-solving activities are only one part of the puzzle. While a great method can help unlock your team’s ability to solve problems, without a thoughtful approach and strong facilitation the solutions may not be fit for purpose.

Let’s take a look at some problem-solving tips you can apply to any process to help it be a success!

Clearly define the problem

Jumping straight to solutions can be tempting, though without first clearly articulating a problem, the solution might not be the right one. Many of the problem-solving activities below include sections where the problem is explored and clearly defined before moving on.

This is a vital part of the problem-solving process and taking the time to fully define an issue can save time and effort later. A clear definition helps identify irrelevant information and it also ensures that your team sets off on the right track.

Don’t jump to conclusions

It’s easy for groups to exhibit cognitive bias or have preconceived ideas about both problems and potential solutions. Be sure to back up any problem statements or potential solutions with facts, research, and adequate forethought.

The best techniques ask participants to be methodical and challenge preconceived notions. Make sure you give the group enough time and space to collect relevant information and consider the problem in a new way. By approaching the process with a clear, rational mindset, you’ll often find that better solutions are more forthcoming.

Try different approaches

Problems come in all shapes and sizes and so too should the methods you use to solve them. If you find that one approach isn’t yielding results and your team isn’t finding different solutions, try mixing it up. You’ll be surprised at how using a new creative activity can unblock your team and generate great solutions.

Don’t take it personally

Depending on the nature of your team or organizational problems, it’s easy for conversations to get heated. While it’s good for participants to be engaged in the discussions, ensure that emotions don’t run too high and that blame isn’t thrown around while finding solutions.

You’re all in it together, and even if your team or area is seeing problems, that isn’t necessarily a disparagement of you personally. Using facilitation skills to manage group dynamics is one effective method of helping conversations be more constructive.

Get the right people in the room

Your problem-solving method is often only as effective as the group using it. Getting the right people on the job and managing the number of people present is important too!

If the group is too small, you may not get enough different perspectives to effectively solve a problem. If the group is too large, you can go round and round during the ideation stages.

Creating the right group makeup is also important in ensuring you have the necessary expertise and skillset to both identify and follow up on potential solutions. Carefully consider who to include at each stage to help ensure your problem-solving method is followed and positioned for success.

Document everything

The best solutions can take refinement, iteration, and reflection to come out. Get into a habit of documenting your process in order to keep all the learnings from the session and to allow ideas to mature and develop. Many of the methods below involve the creation of documents or shared resources. Be sure to keep and share these so everyone can benefit from the work done!

Bring a facilitator

Facilitation is all about making group processes easier. With a subject as potentially emotive and important as problem-solving, having an impartial third party in the form of a facilitator can make all the difference in finding great solutions and keeping the process moving. Consider bringing a facilitator to your problem-solving session to get better results and generate meaningful solutions!

Develop your problem-solving skills

It takes time and practice to be an effective problem solver. While some roles or participants might more naturally gravitate towards problem-solving, it can take development and planning to help everyone create better solutions.

You might develop a training program, run a problem-solving workshop or simply ask your team to practice using the techniques below. Check out our post on problem-solving skills to see how you and your group can develop the right mental process and be more resilient to issues too!

Design a great agenda

Workshops are a great format for solving problems. With the right approach, you can focus a group and help them find the solutions to their own problems. But designing a process can be time-consuming and finding the right activities can be difficult.

Check out our workshop planning guide to level-up your agenda design and start running more effective workshops. Need inspiration? Check out templates designed by expert facilitators to help you kickstart your process!

In this section, we’ll look at in-depth problem-solving methods that provide a complete end-to-end process for developing effective solutions. These will help guide your team from the discovery and definition of a problem through to delivering the right solution.

If you’re looking for an all-encompassing method or problem-solving model, these processes are a great place to start. They’ll ask your team to challenge preconceived ideas and adopt a mindset for solving problems more effectively.

Six Thinking Hats
Lightning Decision Jam
Problem Definition Process
Discovery & Action Dialogue

Design Sprint 2.0

Open Space Technology

1. Six Thinking Hats

Individual approaches to solving a problem can be very different based on what team or role an individual holds. It can be easy for existing biases or perspectives to find their way into the mix, or for internal politics to direct a conversation.

Six Thinking Hats is a classic method for identifying the problems that need to be solved and enables your team to consider them from different angles, whether that is by focusing on facts and data, creative solutions, or by considering why a particular solution might not work.

Like all problem-solving frameworks, Six Thinking Hats is effective at helping teams remove roadblocks from a conversation or discussion and come to terms with all the aspects necessary to solve complex problems.

2. Lightning Decision Jam

Featured courtesy of Jonathan Courtney of AJ&Smart Berlin, Lightning Decision Jam is one of those strategies that should be in every facilitation toolbox. Exploring problems and finding solutions is often creative in nature, though as with any creative process, there is the potential to lose focus and get lost.

Unstructured discussions might get you there in the end, but it’s much more effective to use a method that creates a clear process and team focus.

In Lightning Decision Jam, participants are invited to begin by writing challenges, concerns, or mistakes on post-its without discussing them before then being invited by the moderator to present them to the group.

From there, the team vote on which problems to solve and are guided through steps that will allow them to reframe those problems, create solutions and then decide what to execute on.

By deciding the problems that need to be solved as a team before moving on, this group process is great for ensuring the whole team is aligned and can take ownership over the next stages.

Lightning Decision Jam (LDJ) #action #decision making #problem solving #issue analysis #innovation #design #remote-friendly The problem with anything that requires creative thinking is that it’s easy to get lost—lose focus and fall into the trap of having useless, open-ended, unstructured discussions. Here’s the most effective solution I’ve found: Replace all open, unstructured discussion with a clear process. What to use this exercise for: Anything which requires a group of people to make decisions, solve problems or discuss challenges. It’s always good to frame an LDJ session with a broad topic, here are some examples: The conversion flow of our checkout Our internal design process How we organise events Keeping up with our competition Improving sales flow

3. Problem Definition Process

While problems can be complex, the problem-solving methods you use to identify and solve those problems can often be simple in design.

By taking the time to truly identify and define a problem before asking the group to reframe the challenge as an opportunity, this method is a great way to enable change.

Begin by identifying a focus question and exploring the ways in which it manifests before splitting into five teams who will each consider the problem using a different method: escape, reversal, exaggeration, distortion or wishful. Teams develop a problem objective and create ideas in line with their method before then feeding them back to the group.

This method is great for enabling in-depth discussions while also creating space for finding creative solutions too!

Problem Definition #problem solving #idea generation #creativity #online #remote-friendly A problem solving technique to define a problem, challenge or opportunity and to generate ideas.

4. The 5 Whys

Sometimes, a group needs to go further with their strategies and analyze the root cause at the heart of organizational issues. An RCA or root cause analysis is the process of identifying what is at the heart of business problems or recurring challenges.

The 5 Whys is a simple and effective method of helping a group go find the root cause of any problem or challenge and conduct analysis that will deliver results.

By beginning with the creation of a problem statement and going through five stages to refine it, The 5 Whys provides everything you need to truly discover the cause of an issue.

The 5 Whys #hyperisland #innovation This simple and powerful method is useful for getting to the core of a problem or challenge. As the title suggests, the group defines a problems, then asks the question “why” five times, often using the resulting explanation as a starting point for creative problem solving.

5. World Cafe

World Cafe is a simple but powerful facilitation technique to help bigger groups to focus their energy and attention on solving complex problems.

World Cafe enables this approach by creating a relaxed atmosphere where participants are able to self-organize and explore topics relevant and important to them which are themed around a central problem-solving purpose. Create the right atmosphere by modeling your space after a cafe and after guiding the group through the method, let them take the lead!

Making problem-solving a part of your organization’s culture in the long term can be a difficult undertaking. More approachable formats like World Cafe can be especially effective in bringing people unfamiliar with workshops into the fold.

World Cafe #hyperisland #innovation #issue analysis World Café is a simple yet powerful method, originated by Juanita Brown, for enabling meaningful conversations driven completely by participants and the topics that are relevant and important to them. Facilitators create a cafe-style space and provide simple guidelines. Participants then self-organize and explore a set of relevant topics or questions for conversation.

6. Discovery & Action Dialogue (DAD)

One of the best approaches is to create a safe space for a group to share and discover practices and behaviors that can help them find their own solutions.

With DAD, you can help a group choose which problems they wish to solve and which approaches they will take to do so. It’s great at helping remove resistance to change and can help get buy-in at every level too!

This process of enabling frontline ownership is great in ensuring follow-through and is one of the methods you will want in your toolbox as a facilitator.

Discovery & Action Dialogue (DAD) #idea generation #liberating structures #action #issue analysis #remote-friendly DADs make it easy for a group or community to discover practices and behaviors that enable some individuals (without access to special resources and facing the same constraints) to find better solutions than their peers to common problems. These are called positive deviant (PD) behaviors and practices. DADs make it possible for people in the group, unit, or community to discover by themselves these PD practices. DADs also create favorable conditions for stimulating participants’ creativity in spaces where they can feel safe to invent new and more effective practices. Resistance to change evaporates as participants are unleashed to choose freely which practices they will adopt or try and which problems they will tackle. DADs make it possible to achieve frontline ownership of solutions.

7. Design Sprint 2.0

Want to see how a team can solve big problems and move forward with prototyping and testing solutions in a few days? The Design Sprint 2.0 template from Jake Knapp, author of Sprint, is a complete agenda for a with proven results.

Developing the right agenda can involve difficult but necessary planning. Ensuring all the correct steps are followed can also be stressful or time-consuming depending on your level of experience.

Use this complete 4-day workshop template if you are finding there is no obvious solution to your challenge and want to focus your team around a specific problem that might require a shortcut to launching a minimum viable product or waiting for the organization-wide implementation of a solution.

8. Open space technology

Open space technology- developed by Harrison Owen – creates a space where large groups are invited to take ownership of their problem solving and lead individual sessions. Open space technology is a great format when you have a great deal of expertise and insight in the room and want to allow for different takes and approaches on a particular theme or problem you need to be solved.

Start by bringing your participants together to align around a central theme and focus their efforts. Explain the ground rules to help guide the problem-solving process and then invite members to identify any issue connecting to the central theme that they are interested in and are prepared to take responsibility for.

Once participants have decided on their approach to the core theme, they write their issue on a piece of paper, announce it to the group, pick a session time and place, and post the paper on the wall. As the wall fills up with sessions, the group is then invited to join the sessions that interest them the most and which they can contribute to, then you’re ready to begin!

Everyone joins the problem-solving group they’ve signed up to, record the discussion and if appropriate, findings can then be shared with the rest of the group afterward.

Open Space Technology #action plan #idea generation #problem solving #issue analysis #large group #online #remote-friendly Open Space is a methodology for large groups to create their agenda discerning important topics for discussion, suitable for conferences, community gatherings and whole system facilitation

Techniques to identify and analyze problems

Using a problem-solving method to help a team identify and analyze a problem can be a quick and effective addition to any workshop or meeting.

While further actions are always necessary, you can generate momentum and alignment easily, and these activities are a great place to get started.

We’ve put together this list of techniques to help you and your team with problem identification, analysis, and discussion that sets the foundation for developing effective solutions.

Let’s take a look!

The Creativity Dice
Fishbone Analysis
Problem Tree
SWOT Analysis
Agreement-Certainty Matrix
The Journalistic Six
LEGO Challenge
What, So What, Now What?
Journalists

Individual and group perspectives are incredibly important, but what happens if people are set in their minds and need a change of perspective in order to approach a problem more effectively?

Flip It is a method we love because it is both simple to understand and run, and allows groups to understand how their perspectives and biases are formed.

Participants in Flip It are first invited to consider concerns, issues, or problems from a perspective of fear and write them on a flip chart. Then, the group is asked to consider those same issues from a perspective of hope and flip their understanding.

No problem and solution is free from existing bias and by changing perspectives with Flip It, you can then develop a problem solving model quickly and effectively.

Flip It! #gamestorming #problem solving #action Often, a change in a problem or situation comes simply from a change in our perspectives. Flip It! is a quick game designed to show players that perspectives are made, not born.

10. The Creativity Dice

One of the most useful problem solving skills you can teach your team is of approaching challenges with creativity, flexibility, and openness. Games like The Creativity Dice allow teams to overcome the potential hurdle of too much linear thinking and approach the process with a sense of fun and speed.

In The Creativity Dice, participants are organized around a topic and roll a dice to determine what they will work on for a period of 3 minutes at a time. They might roll a 3 and work on investigating factual information on the chosen topic. They might roll a 1 and work on identifying the specific goals, standards, or criteria for the session.

Encouraging rapid work and iteration while asking participants to be flexible are great skills to cultivate. Having a stage for idea incubation in this game is also important. Moments of pause can help ensure the ideas that are put forward are the most suitable.

The Creativity Dice #creativity #problem solving #thiagi #issue analysis Too much linear thinking is hazardous to creative problem solving. To be creative, you should approach the problem (or the opportunity) from different points of view. You should leave a thought hanging in mid-air and move to another. This skipping around prevents premature closure and lets your brain incubate one line of thought while you consciously pursue another.

11. Fishbone Analysis

Organizational or team challenges are rarely simple, and it’s important to remember that one problem can be an indication of something that goes deeper and may require further consideration to be solved.

Fishbone Analysis helps groups to dig deeper and understand the origins of a problem. It’s a great example of a root cause analysis method that is simple for everyone on a team to get their head around.

Participants in this activity are asked to annotate a diagram of a fish, first adding the problem or issue to be worked on at the head of a fish before then brainstorming the root causes of the problem and adding them as bones on the fish.

Using abstractions such as a diagram of a fish can really help a team break out of their regular thinking and develop a creative approach.

Fishbone Analysis #problem solving ##root cause analysis #decision making #online facilitation A process to help identify and understand the origins of problems, issues or observations.

12. Problem Tree

Encouraging visual thinking can be an essential part of many strategies. By simply reframing and clarifying problems, a group can move towards developing a problem solving model that works for them.

In Problem Tree, groups are asked to first brainstorm a list of problems – these can be design problems, team problems or larger business problems – and then organize them into a hierarchy. The hierarchy could be from most important to least important or abstract to practical, though the key thing with problem solving games that involve this aspect is that your group has some way of managing and sorting all the issues that are raised.

Once you have a list of problems that need to be solved and have organized them accordingly, you’re then well-positioned for the next problem solving steps.

Problem tree #define intentions #create #design #issue analysis A problem tree is a tool to clarify the hierarchy of problems addressed by the team within a design project; it represents high level problems or related sublevel problems.

13. SWOT Analysis

Chances are you’ve heard of the SWOT Analysis before. This problem-solving method focuses on identifying strengths, weaknesses, opportunities, and threats is a tried and tested method for both individuals and teams.

Start by creating a desired end state or outcome and bare this in mind – any process solving model is made more effective by knowing what you are moving towards. Create a quadrant made up of the four categories of a SWOT analysis and ask participants to generate ideas based on each of those quadrants.

Once you have those ideas assembled in their quadrants, cluster them together based on their affinity with other ideas. These clusters are then used to facilitate group conversations and move things forward.

SWOT analysis #gamestorming #problem solving #action #meeting facilitation The SWOT Analysis is a long-standing technique of looking at what we have, with respect to the desired end state, as well as what we could improve on. It gives us an opportunity to gauge approaching opportunities and dangers, and assess the seriousness of the conditions that affect our future. When we understand those conditions, we can influence what comes next.

14. Agreement-Certainty Matrix

Not every problem-solving approach is right for every challenge, and deciding on the right method for the challenge at hand is a key part of being an effective team.

The Agreement Certainty matrix helps teams align on the nature of the challenges facing them. By sorting problems from simple to chaotic, your team can understand what methods are suitable for each problem and what they can do to ensure effective results.

If you are already using Liberating Structures techniques as part of your problem-solving strategy, the Agreement-Certainty Matrix can be an invaluable addition to your process. We’ve found it particularly if you are having issues with recurring problems in your organization and want to go deeper in understanding the root cause.

Agreement-Certainty Matrix #issue analysis #liberating structures #problem solving You can help individuals or groups avoid the frequent mistake of trying to solve a problem with methods that are not adapted to the nature of their challenge. The combination of two questions makes it possible to easily sort challenges into four categories: simple, complicated, complex , and chaotic . A problem is simple when it can be solved reliably with practices that are easy to duplicate. It is complicated when experts are required to devise a sophisticated solution that will yield the desired results predictably. A problem is complex when there are several valid ways to proceed but outcomes are not predictable in detail. Chaotic is when the context is too turbulent to identify a path forward. A loose analogy may be used to describe these differences: simple is like following a recipe, complicated like sending a rocket to the moon, complex like raising a child, and chaotic is like the game “Pin the Tail on the Donkey.” The Liberating Structures Matching Matrix in Chapter 5 can be used as the first step to clarify the nature of a challenge and avoid the mismatches between problems and solutions that are frequently at the root of chronic, recurring problems.

Organizing and charting a team’s progress can be important in ensuring its success. SQUID (Sequential Question and Insight Diagram) is a great model that allows a team to effectively switch between giving questions and answers and develop the skills they need to stay on track throughout the process.

Begin with two different colored sticky notes – one for questions and one for answers – and with your central topic (the head of the squid) on the board. Ask the group to first come up with a series of questions connected to their best guess of how to approach the topic. Ask the group to come up with answers to those questions, fix them to the board and connect them with a line. After some discussion, go back to question mode by responding to the generated answers or other points on the board.

It’s rewarding to see a diagram grow throughout the exercise, and a completed SQUID can provide a visual resource for future effort and as an example for other teams.

SQUID #gamestorming #project planning #issue analysis #problem solving When exploring an information space, it’s important for a group to know where they are at any given time. By using SQUID, a group charts out the territory as they go and can navigate accordingly. SQUID stands for Sequential Question and Insight Diagram.

16. Speed Boat

To continue with our nautical theme, Speed Boat is a short and sweet activity that can help a team quickly identify what employees, clients or service users might have a problem with and analyze what might be standing in the way of achieving a solution.

Methods that allow for a group to make observations, have insights and obtain those eureka moments quickly are invaluable when trying to solve complex problems.

In Speed Boat, the approach is to first consider what anchors and challenges might be holding an organization (or boat) back. Bonus points if you are able to identify any sharks in the water and develop ideas that can also deal with competitors!

Speed Boat #gamestorming #problem solving #action Speedboat is a short and sweet way to identify what your employees or clients don’t like about your product/service or what’s standing in the way of a desired goal.

17. The Journalistic Six

Some of the most effective ways of solving problems is by encouraging teams to be more inclusive and diverse in their thinking.

Based on the six key questions journalism students are taught to answer in articles and news stories, The Journalistic Six helps create teams to see the whole picture. By using who, what, when, where, why, and how to facilitate the conversation and encourage creative thinking, your team can make sure that the problem identification and problem analysis stages of the are covered exhaustively and thoughtfully. Reporter’s notebook and dictaphone optional.

The Journalistic Six – Who What When Where Why How #idea generation #issue analysis #problem solving #online #creative thinking #remote-friendly A questioning method for generating, explaining, investigating ideas.

18. LEGO Challenge

Now for an activity that is a little out of the (toy) box. LEGO Serious Play is a facilitation methodology that can be used to improve creative thinking and problem-solving skills.

The LEGO Challenge includes giving each member of the team an assignment that is hidden from the rest of the group while they create a structure without speaking.

What the LEGO challenge brings to the table is a fun working example of working with stakeholders who might not be on the same page to solve problems. Also, it’s LEGO! Who doesn’t love LEGO!

LEGO Challenge #hyperisland #team A team-building activity in which groups must work together to build a structure out of LEGO, but each individual has a secret “assignment” which makes the collaborative process more challenging. It emphasizes group communication, leadership dynamics, conflict, cooperation, patience and problem solving strategy.

19. What, So What, Now What?

If not carefully managed, the problem identification and problem analysis stages of the problem-solving process can actually create more problems and misunderstandings.

The What, So What, Now What? problem-solving activity is designed to help collect insights and move forward while also eliminating the possibility of disagreement when it comes to identifying, clarifying, and analyzing organizational or work problems.

Facilitation is all about bringing groups together so that might work on a shared goal and the best problem-solving strategies ensure that teams are aligned in purpose, if not initially in opinion or insight.

Throughout the three steps of this game, you give everyone on a team to reflect on a problem by asking what happened, why it is important, and what actions should then be taken.

This can be a great activity for bringing our individual perceptions about a problem or challenge and contextualizing it in a larger group setting. This is one of the most important problem-solving skills you can bring to your organization.

W³ – What, So What, Now What? #issue analysis #innovation #liberating structures You can help groups reflect on a shared experience in a way that builds understanding and spurs coordinated action while avoiding unproductive conflict. It is possible for every voice to be heard while simultaneously sifting for insights and shaping new direction. Progressing in stages makes this practical—from collecting facts about What Happened to making sense of these facts with So What and finally to what actions logically follow with Now What . The shared progression eliminates most of the misunderstandings that otherwise fuel disagreements about what to do. Voila!

20. Journalists

Problem analysis can be one of the most important and decisive stages of all problem-solving tools. Sometimes, a team can become bogged down in the details and are unable to move forward.

Journalists is an activity that can avoid a group from getting stuck in the problem identification or problem analysis stages of the process.

In Journalists, the group is invited to draft the front page of a fictional newspaper and figure out what stories deserve to be on the cover and what headlines those stories will have. By reframing how your problems and challenges are approached, you can help a team move productively through the process and be better prepared for the steps to follow.

Journalists #vision #big picture #issue analysis #remote-friendly This is an exercise to use when the group gets stuck in details and struggles to see the big picture. Also good for defining a vision.

Problem-solving techniques for developing solutions

The success of any problem-solving process can be measured by the solutions it produces. After you’ve defined the issue, explored existing ideas, and ideated, it’s time to narrow down to the correct solution.

Use these problem-solving techniques when you want to help your team find consensus, compare possible solutions, and move towards taking action on a particular problem.

Improved Solutions
Four-Step Sketch
15% Solutions
How-Now-Wow matrix
Impact Effort Matrix

21. Mindspin

Brainstorming is part of the bread and butter of the problem-solving process and all problem-solving strategies benefit from getting ideas out and challenging a team to generate solutions quickly.

With Mindspin, participants are encouraged not only to generate ideas but to do so under time constraints and by slamming down cards and passing them on. By doing multiple rounds, your team can begin with a free generation of possible solutions before moving on to developing those solutions and encouraging further ideation.

This is one of our favorite problem-solving activities and can be great for keeping the energy up throughout the workshop. Remember the importance of helping people become engaged in the process – energizing problem-solving techniques like Mindspin can help ensure your team stays engaged and happy, even when the problems they’re coming together to solve are complex.

MindSpin #teampedia #idea generation #problem solving #action A fast and loud method to enhance brainstorming within a team. Since this activity has more than round ideas that are repetitive can be ruled out leaving more creative and innovative answers to the challenge.

22. Improved Solutions

After a team has successfully identified a problem and come up with a few solutions, it can be tempting to call the work of the problem-solving process complete. That said, the first solution is not necessarily the best, and by including a further review and reflection activity into your problem-solving model, you can ensure your group reaches the best possible result.

One of a number of problem-solving games from Thiagi Group, Improved Solutions helps you go the extra mile and develop suggested solutions with close consideration and peer review. By supporting the discussion of several problems at once and by shifting team roles throughout, this problem-solving technique is a dynamic way of finding the best solution.

Improved Solutions #creativity #thiagi #problem solving #action #team You can improve any solution by objectively reviewing its strengths and weaknesses and making suitable adjustments. In this creativity framegame, you improve the solutions to several problems. To maintain objective detachment, you deal with a different problem during each of six rounds and assume different roles (problem owner, consultant, basher, booster, enhancer, and evaluator) during each round. At the conclusion of the activity, each player ends up with two solutions to her problem.

23. Four Step Sketch

Creative thinking and visual ideation does not need to be confined to the opening stages of your problem-solving strategies. Exercises that include sketching and prototyping on paper can be effective at the solution finding and development stage of the process, and can be great for keeping a team engaged.

By going from simple notes to a crazy 8s round that involves rapidly sketching 8 variations on their ideas before then producing a final solution sketch, the group is able to iterate quickly and visually. Problem-solving techniques like Four-Step Sketch are great if you have a group of different thinkers and want to change things up from a more textual or discussion-based approach.

Four-Step Sketch #design sprint #innovation #idea generation #remote-friendly The four-step sketch is an exercise that helps people to create well-formed concepts through a structured process that includes: Review key information Start design work on paper, Consider multiple variations , Create a detailed solution . This exercise is preceded by a set of other activities allowing the group to clarify the challenge they want to solve. See how the Four Step Sketch exercise fits into a Design Sprint

24. 15% Solutions

Some problems are simpler than others and with the right problem-solving activities, you can empower people to take immediate actions that can help create organizational change.

Part of the liberating structures toolkit, 15% solutions is a problem-solving technique that focuses on finding and implementing solutions quickly. A process of iterating and making small changes quickly can help generate momentum and an appetite for solving complex problems.

Problem-solving strategies can live and die on whether people are onboard. Getting some quick wins is a great way of getting people behind the process.

It can be extremely empowering for a team to realize that problem-solving techniques can be deployed quickly and easily and delineate between things they can positively impact and those things they cannot change.

15% Solutions #action #liberating structures #remote-friendly You can reveal the actions, however small, that everyone can do immediately. At a minimum, these will create momentum, and that may make a BIG difference. 15% Solutions show that there is no reason to wait around, feel powerless, or fearful. They help people pick it up a level. They get individuals and the group to focus on what is within their discretion instead of what they cannot change. With a very simple question, you can flip the conversation to what can be done and find solutions to big problems that are often distributed widely in places not known in advance. Shifting a few grains of sand may trigger a landslide and change the whole landscape.

25. How-Now-Wow Matrix

The problem-solving process is often creative, as complex problems usually require a change of thinking and creative response in order to find the best solutions. While it’s common for the first stages to encourage creative thinking, groups can often gravitate to familiar solutions when it comes to the end of the process.

When selecting solutions, you don’t want to lose your creative energy! The How-Now-Wow Matrix from Gamestorming is a great problem-solving activity that enables a group to stay creative and think out of the box when it comes to selecting the right solution for a given problem.

Problem-solving techniques that encourage creative thinking and the ideation and selection of new solutions can be the most effective in organisational change. Give the How-Now-Wow Matrix a go, and not just for how pleasant it is to say out loud.

How-Now-Wow Matrix #gamestorming #idea generation #remote-friendly When people want to develop new ideas, they most often think out of the box in the brainstorming or divergent phase. However, when it comes to convergence, people often end up picking ideas that are most familiar to them. This is called a ‘creative paradox’ or a ‘creadox’. The How-Now-Wow matrix is an idea selection tool that breaks the creadox by forcing people to weigh each idea on 2 parameters.

26. Impact and Effort Matrix

All problem-solving techniques hope to not only find solutions to a given problem or challenge but to find the best solution. When it comes to finding a solution, groups are invited to put on their decision-making hats and really think about how a proposed idea would work in practice.

The Impact and Effort Matrix is one of the problem-solving techniques that fall into this camp, empowering participants to first generate ideas and then categorize them into a 2×2 matrix based on impact and effort.

Activities that invite critical thinking while remaining simple are invaluable. Use the Impact and Effort Matrix to move from ideation and towards evaluating potential solutions before then committing to them.

Impact and Effort Matrix #gamestorming #decision making #action #remote-friendly In this decision-making exercise, possible actions are mapped based on two factors: effort required to implement and potential impact. Categorizing ideas along these lines is a useful technique in decision making, as it obliges contributors to balance and evaluate suggested actions before committing to them.

27. Dotmocracy

If you’ve followed each of the problem-solving steps with your group successfully, you should move towards the end of your process with heaps of possible solutions developed with a specific problem in mind. But how do you help a group go from ideation to putting a solution into action?

Dotmocracy – or Dot Voting -is a tried and tested method of helping a team in the problem-solving process make decisions and put actions in place with a degree of oversight and consensus.

One of the problem-solving techniques that should be in every facilitator’s toolbox, Dot Voting is fast and effective and can help identify the most popular and best solutions and help bring a group to a decision effectively.

Dotmocracy #action #decision making #group prioritization #hyperisland #remote-friendly Dotmocracy is a simple method for group prioritization or decision-making. It is not an activity on its own, but a method to use in processes where prioritization or decision-making is the aim. The method supports a group to quickly see which options are most popular or relevant. The options or ideas are written on post-its and stuck up on a wall for the whole group to see. Each person votes for the options they think are the strongest, and that information is used to inform a decision.

All facilitators know that warm-ups and icebreakers are useful for any workshop or group process. Problem-solving workshops are no different.

Use these problem-solving techniques to warm up a group and prepare them for the rest of the process. Activating your group by tapping into some of the top problem-solving skills can be one of the best ways to see great outcomes from your session.

Check-in/Check-out
Doodling Together
Show and Tell
Constellations
Draw a Tree

28. Check-in / Check-out

Solid processes are planned from beginning to end, and the best facilitators know that setting the tone and establishing a safe, open environment can be integral to a successful problem-solving process.

Check-in / Check-out is a great way to begin and/or bookend a problem-solving workshop. Checking in to a session emphasizes that everyone will be seen, heard, and expected to contribute.

If you are running a series of meetings, setting a consistent pattern of checking in and checking out can really help your team get into a groove. We recommend this opening-closing activity for small to medium-sized groups though it can work with large groups if they’re disciplined!

Check-in / Check-out #team #opening #closing #hyperisland #remote-friendly Either checking-in or checking-out is a simple way for a team to open or close a process, symbolically and in a collaborative way. Checking-in/out invites each member in a group to be present, seen and heard, and to express a reflection or a feeling. Checking-in emphasizes presence, focus and group commitment; checking-out emphasizes reflection and symbolic closure.

29. Doodling Together

Thinking creatively and not being afraid to make suggestions are important problem-solving skills for any group or team, and warming up by encouraging these behaviors is a great way to start.

Doodling Together is one of our favorite creative ice breaker games – it’s quick, effective, and fun and can make all following problem-solving steps easier by encouraging a group to collaborate visually. By passing cards and adding additional items as they go, the workshop group gets into a groove of co-creation and idea development that is crucial to finding solutions to problems.

Doodling Together #collaboration #creativity #teamwork #fun #team #visual methods #energiser #icebreaker #remote-friendly Create wild, weird and often funny postcards together & establish a group’s creative confidence.

30. Show and Tell

You might remember some version of Show and Tell from being a kid in school and it’s a great problem-solving activity to kick off a session.

Asking participants to prepare a little something before a workshop by bringing an object for show and tell can help them warm up before the session has even begun! Games that include a physical object can also help encourage early engagement before moving onto more big-picture thinking.

By asking your participants to tell stories about why they chose to bring a particular item to the group, you can help teams see things from new perspectives and see both differences and similarities in the way they approach a topic. Great groundwork for approaching a problem-solving process as a team!

Show and Tell #gamestorming #action #opening #meeting facilitation Show and Tell taps into the power of metaphors to reveal players’ underlying assumptions and associations around a topic The aim of the game is to get a deeper understanding of stakeholders’ perspectives on anything—a new project, an organizational restructuring, a shift in the company’s vision or team dynamic.

31. Constellations

Who doesn’t love stars? Constellations is a great warm-up activity for any workshop as it gets people up off their feet, energized, and ready to engage in new ways with established topics. It’s also great for showing existing beliefs, biases, and patterns that can come into play as part of your session.

Using warm-up games that help build trust and connection while also allowing for non-verbal responses can be great for easing people into the problem-solving process and encouraging engagement from everyone in the group. Constellations is great in large spaces that allow for movement and is definitely a practical exercise to allow the group to see patterns that are otherwise invisible.

Constellations #trust #connection #opening #coaching #patterns #system Individuals express their response to a statement or idea by standing closer or further from a central object. Used with teams to reveal system, hidden patterns, perspectives.

32. Draw a Tree

Problem-solving games that help raise group awareness through a central, unifying metaphor can be effective ways to warm-up a group in any problem-solving model.

Draw a Tree is a simple warm-up activity you can use in any group and which can provide a quick jolt of energy. Start by asking your participants to draw a tree in just 45 seconds – they can choose whether it will be abstract or realistic.

Once the timer is up, ask the group how many people included the roots of the tree and use this as a means to discuss how we can ignore important parts of any system simply because they are not visible.

All problem-solving strategies are made more effective by thinking of problems critically and by exposing things that may not normally come to light. Warm-up games like Draw a Tree are great in that they quickly demonstrate some key problem-solving skills in an accessible and effective way.

Draw a Tree #thiagi #opening #perspectives #remote-friendly With this game you can raise awarness about being more mindful, and aware of the environment we live in.

Each step of the problem-solving workshop benefits from an intelligent deployment of activities, games, and techniques. Bringing your session to an effective close helps ensure that solutions are followed through on and that you also celebrate what has been achieved.

Here are some problem-solving activities you can use to effectively close a workshop or meeting and ensure the great work you’ve done can continue afterward.

One Breath Feedback
Who What When Matrix
Response Cards

How do I conclude a problem-solving process?

All good things must come to an end. With the bulk of the work done, it can be tempting to conclude your workshop swiftly and without a moment to debrief and align. This can be problematic in that it doesn’t allow your team to fully process the results or reflect on the process.

At the end of an effective session, your team will have gone through a process that, while productive, can be exhausting. It’s important to give your group a moment to take a breath, ensure that they are clear on future actions, and provide short feedback before leaving the space.

The primary purpose of any problem-solving method is to generate solutions and then implement them. Be sure to take the opportunity to ensure everyone is aligned and ready to effectively implement the solutions you produced in the workshop.

Remember that every process can be improved and by giving a short moment to collect feedback in the session, you can further refine your problem-solving methods and see further success in the future too.

33. One Breath Feedback

Maintaining attention and focus during the closing stages of a problem-solving workshop can be tricky and so being concise when giving feedback can be important. It’s easy to incur “death by feedback” should some team members go on for too long sharing their perspectives in a quick feedback round.

One Breath Feedback is a great closing activity for workshops. You give everyone an opportunity to provide feedback on what they’ve done but only in the space of a single breath. This keeps feedback short and to the point and means that everyone is encouraged to provide the most important piece of feedback to them.

One breath feedback #closing #feedback #action This is a feedback round in just one breath that excels in maintaining attention: each participants is able to speak during just one breath … for most people that’s around 20 to 25 seconds … unless of course you’ve been a deep sea diver in which case you’ll be able to do it for longer.

34. Who What When Matrix

Matrices feature as part of many effective problem-solving strategies and with good reason. They are easily recognizable, simple to use, and generate results.

The Who What When Matrix is a great tool to use when closing your problem-solving session by attributing a who, what and when to the actions and solutions you have decided upon. The resulting matrix is a simple, easy-to-follow way of ensuring your team can move forward.

Great solutions can’t be enacted without action and ownership. Your problem-solving process should include a stage for allocating tasks to individuals or teams and creating a realistic timeframe for those solutions to be implemented or checked out. Use this method to keep the solution implementation process clear and simple for all involved.

Who/What/When Matrix #gamestorming #action #project planning With Who/What/When matrix, you can connect people with clear actions they have defined and have committed to.

35. Response cards

Group discussion can comprise the bulk of most problem-solving activities and by the end of the process, you might find that your team is talked out!

Providing a means for your team to give feedback with short written notes can ensure everyone is head and can contribute without the need to stand up and talk. Depending on the needs of the group, giving an alternative can help ensure everyone can contribute to your problem-solving model in the way that makes the most sense for them.

Response Cards is a great way to close a workshop if you are looking for a gentle warm-down and want to get some swift discussion around some of the feedback that is raised.

Response Cards #debriefing #closing #structured sharing #questions and answers #thiagi #action It can be hard to involve everyone during a closing of a session. Some might stay in the background or get unheard because of louder participants. However, with the use of Response Cards, everyone will be involved in providing feedback or clarify questions at the end of a session.

Save time and effort discovering the right solutions

A structured problem solving process is a surefire way of solving tough problems, discovering creative solutions and driving organizational change. But how can you design for successful outcomes?

With SessionLab, it’s easy to design engaging workshops that deliver results. Drag, drop and reorder blocks to build your agenda. When you make changes or update your agenda, your session timing adjusts automatically , saving you time on manual adjustments.

Collaborating with stakeholders or clients? Share your agenda with a single click and collaborate in real-time. No more sending documents back and forth over email.

Explore how to use SessionLab to design effective problem solving workshops or watch this five minute video to see the planner in action!

Over to you

The problem-solving process can often be as complicated and multifaceted as the problems they are set-up to solve. With the right problem-solving techniques and a mix of creative exercises designed to guide discussion and generate purposeful ideas, we hope we’ve given you the tools to find the best solutions as simply and easily as possible.

Is there a problem-solving technique that you are missing here? Do you have a favorite activity or method you use when facilitating? Let us know in the comments below, we’d love to hear from you!

thank you very much for these excellent techniques

Certainly wonderful article, very detailed. Shared!

Your list of techniques for problem solving can be helpfully extended by adding TRIZ to the list of techniques. TRIZ has 40 problem solving techniques derived from methods inventros and patent holders used to get new patents. About 10-12 are general approaches. many organization sponsor classes in TRIZ that are used to solve business problems or general organiztational problems. You can take a look at TRIZ and dwonload a free internet booklet to see if you feel it shound be included per your selection process.

Design your next workshop with SessionLab

Join the 150,000 facilitators using SessionLab

School Guide
Mathematics
Number System and Arithmetic
Trigonometry
Probability
Mensuration
Maths Formulas
Class 8 Maths Notes
Class 9 Maths Notes
Class 10 Maths Notes
Class 11 Maths Notes
Class 12 Maths Notes
Graphical Solution of Linear Programming Problems
Linear Programming
Solving Linear Inequalities Word Problems
Stars and Bars Algorithms for Competitive Programming
Python | Linear search on list or tuples
Top 50 Dynamic Programming Coding Problems for Interviews
Dynamic Programming (DP) Tutorial with Problems
Program to find all types of Matrix
Dynamic Programming | High-effort vs. Low-effort Tasks Problem
Python | Linear Programming in Pulp
C++ Program for the Fractional Knapsack Problem
Transportation Problem | Set 1 (Introduction)
Algorithms | Dynamic Programming | Question 7
Algorithms | Dynamic Programming | Question 4
Algorithms | Dynamic Programming | Question 3
Algorithms | Dynamic Programming | Question 2
How to begin with Competitive Programming?
Dynamic Programming (DP) on Grids
Knuth's Optimization in Dynamic Programming

Types of Linear Programming Problems

Linear programming is a mathematical technique for optimizing operations under a given set of constraints. The basic goal of linear programming is to maximize or minimize the total numerical value. It is regarded as one of the most essential strategies for determining optimum resource utilization. Linear programming challenges include a variety of problems involving cost minimization and profit maximization, among others. They will be briefly discussed in this article.

The purpose of this article is to provide students with a comprehensive understanding of the different types of linear programming problems and their solutions.

What is Linear Programming?

Linear programming (LP) is a mathematical optimization technique used to maximize or minimize a linear objective function, subject to a set of linear equality and inequality constraints. It is widely used in various fields such as economics, engineering, operations research, and management science to find the best possible outcome given limited resources.

Components of Linear Programming

Components of linear programming include:

Objective Function: This is a linear function that needs to be optimized (maximized or minimized). It represents the quantity to be maximized or minimized, such as profit, cost, time, etc.
Decision Variables: These are the variables that represent the choices or decisions to be made. They are the unknown quantities that the optimization process seeks to determine. Decision variables must be continuous and can take any real value within a specified range.
Constraints: These are restrictions or limitations on the decision variables that must be satisfied. Constraints can be expressed as linear equations or inequalities. They represent the limitations imposed by available resources, capacity constraints, demand requirements, etc.
Feasible Region: The feasible region is the set of all possible combinations of decision variables that satisfy all constraints. It is defined by the intersection of the constraint boundaries.
Optimal Solution: This is the best possible solution that maximizes or minimizes the objective function while satisfying all constraints. In graphical terms, it is the point within the feasible region that maximizes or minimizes the objective function.

Linear programming provides a systematic and efficient approach to decision-making in situations where resources are limited and objectives need to be optimized.

Different Types of Linear Programming Problems

The following are the types of linear programming problems:

Manufacturing problems
Diet problems
Transportation problems
Optimal alignment problem

Let’s discuss more about each of them.

Manufacturing Problems

In these problems, we evaluate the number of units of various items that should be produced and sold by a company when each product requires a given number of workforce, machine hours, labour hours per unit of product, warehouse space per unit of output, and so on, to maximize profit.

Manufacturing problems involve maximizing the production rate or net profits of manufactured products, which might measure the available workspace, the number of workers, machine hours, packing materials used, raw materials required, the product’s market value, and other factors. These are commonly used in the industrial sector to anticipate a company’s future capital increase over time.

Diet Problems

In these challenges, we assess how many components or nutrients a diet should contain in order to lower the cost of the desired diet while guaranteeing the minimal amount of each vitamin.

As the name suggests, diet-related problems can be resolved by eating more particular foods that are rich in essential nutrients and can support the adoption of a particular diet plan. Finding a set of meals that will satisfy a set of daily nutritional demands for the least amount of money is the aim of a diet problem.

Transportation Problems

In these problems , we create a transportation schedule to discover the most cost-effective method of carrying a product from various plants/factories to various markets.

The study of transportation routes or how items from diverse production sources are transported to various markets to minimize the total transportation cost is linked to transportation difficulties. Analyzing such challenges is crucial for large firms with several production units and a broad customer base.

Optimal Assignment Problems

This problem addresses a company’s completion of a given task/assignment by selecting a specific number of employees to complete the assignment within the required timeframe, assuming that each person works on only one job. Event planning and management in major organizations, for example, are examples of such problems.

Constraints and Objective Function of Each Linear Programming Problem

Steps for solving linear programming problems.

Step 1: Identify the decision variables : The first step is to determine which choice factors control the behaviour of the objective function. A function that needs to be optimised is an objective function. Determine the decision variables and designate them with X, Y, and Z symbols.

Step 2: Form an objective function : Using the decision variables, write out an algebraic expression that displays the quantity we aim to maximize.

Step 3: Identify the constraints : Choose and write the given linear inequalities from the data.

Step 4: Draw the graph for the given data : Construct the graph by using constraints for solving the linear programming problem.

Step 5: Draw the feasible region : Every constraint on the problem is satisfied by this portion of the graph. Anywhere in the feasible zone is a viable solution for the objective function.

Step 6: Choosing the optimal point : Choose the point for which the given function has maximum or minimum values.

Solved Problems of Linear Programming Problems

Question 1. A factory manufactures two types of gadgets, regular and premium. Each gadget requires the use of two operations, assembly and finishing, and there are at most 12 hours available for each operation. A regular gadget requires 1 hour of assembly and 2 hours of finishing, while a premium gadget needs 2 hours of assembly and 1 hour of finishing. Due to other restrictions, the company can make at most 7 gadgets a day. If a profit of $20 is realized for each regular gadget and $30 for a premium gadget, how many of each should be manufactured to maximize profit?

We define our unknowns:

Let the number of regular gadgets manufactured each day = x

and the number of premium gadgets manufactured each day = y

The objective function is

P = 20x + 30y

We now write the constraints. The fourth sentence states that the company can make at most 7 gadgets a day. This translates as

Since the regular gadget requires one hour of assembly and the premium gadget requires two hours of assembly, and there are at most 12 hours available for this operation, we get

x + 2y ≤ 12

Similarly, the regular gadget requires two hours of finishing and the premium gadget one hour. Again, there are at most 12 hours available for finishing. This gives us the following constraint.

2x + y ≤ 12

The fact that x and y can never be negative is represented by the following two constraints:

x ≥ 0, and y ≥ 0.

We have formulated the problem as follows :

Maximize P=20x + 30y Subject to : x + y ≤ 7, x + 2y ≤ 122, x + y ≤ 12, x ≥ 0, y ≥ 0

In order to solve the problem, we next graph the constraints and feasible region.

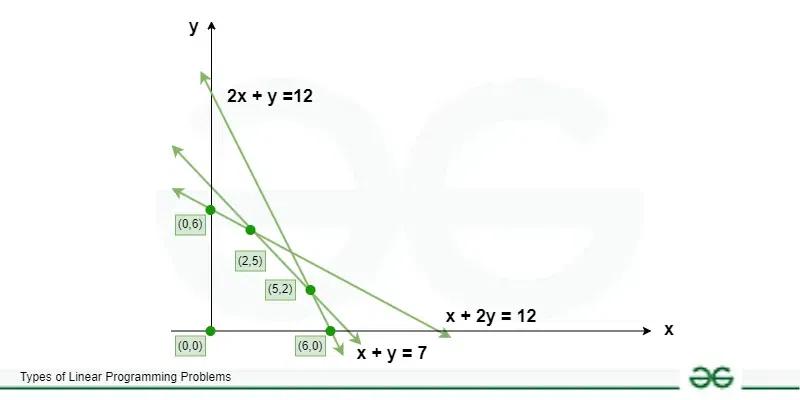
Again, we have shaded the feasible region, where all constraints are satisfied.

Since the extreme value of the objective function always takes place at the vertices of the feasible region, we identify all the critical points. They are listed as (0, 0), (0, 6), (2, 5), (5, 2), and (6, 0). To maximize profit, we will substitute these points in the objective function to see which point gives us the maximum profit each day. The results are listed below.

FAQ on Linear programming

How many methods are there in lpp.

There are different methods to solve a linear programming problem. Such as Graphical method, Simplex method, Ellipsoid method, Interior point methods.

What are the four 4 special cases in linear programming?

Four special cases and difficulties arise at times when using the graphical approach to solving LP problems: (1) infeasibility, (2) unboundedness, (3) redundancy, and (4) alternate optimal solutions.

What are the 3 components of linear programming?

The basic components of the LP are as follows: Decision Variables. Constraints. Objective Functions.

What are the applications of LPP?

LPP applications may include production scheduling, inventory policies, investment portfolio, allocation of advertising budget, construction of warehouses, etc.

What are the limitations of LPP?

Constraints (limitations) should be expressed in mathematical form. Relationships between two or more variables should be linear. The values of the variables should always be non-negative or zero. There should always be finite and infinite inputs and output numbers.

Please Login to comment...

Improve your Coding Skills with Practice

What kind of Experience do you want to share?

Results for "assignment problem"

How to Solve the Assignment Problem: A Complete Guide

Operations Research

Solve the assignment problem with ease using the Hungarian method. Our comprehensive guide walks you through the steps to minimize costs and maximize profits.

Unbalanced Assignment Problem: Definition, Formulation, and Solution Methods

Learn about the Unbalanced Assignment Problem in Operations Research (OR) – its definition, formulation, and solutions. Solve assignment problems with ease!

Maximisation in an Assignment Problem: Optimizing Assignments for Maximum Benefit

Learn how to maximize the benefits associated with each task in an assignment problem. This blog covers everything from understanding the problem to implementing solutions.

Crew Assignment Problem: Optimizing the Allocation of Tasks to Crew Members

Learn about Crew Assignment Problem and how it helps optimize the allocation of tasks to crew members. Explore its benefits, challenges, and real-world applications.

Understanding the Problem with Some Infeasible Assignments in Assignment Models

Learn about infeasible assignments in assignment models, why they occur, and how to deal with them in this informative blog. Ensure your decision-making is not compromised.

Variety of Problems in Job Production: Challenges and Solutions

Management of Machines and Materials

Explore the problems associated with job production, including labor costs, materials management, scheduling complexities, quality control, and resource allocation. Discover solutions to address these challenges and capitalize on the benefits of customization and flexibility offered by job production.

Models in Operations Research: A Comprehensive Guide to Understand and Apply OR Models

Learn about the different types of models used in Operations Research, their advantages and limitations, and how they are applied in real-world scenarios.

Line Balancing Methods: Achieving Efficiency in Production

Discover various line balancing methods used in manufacturing and assembly operations to distribute workload evenly across workstations. Learn how these methods improve efficiency, reduce bottlenecks, and enhance productivity in production processes.

Resource Scheduling and Allocation

Project Management

Learn how to effectively allocate resources to project activities and optimize resource utilization with resource scheduling and allocation techniques. Discover the resource scheduling problem, classification of scheduling problems, and resource allocation methods, including leveling, smoothing, resource-constrained scheduling, and the Critical Chain Method (CCM). Ensure project success by effectively managing resource allocation in your projects.

Designing of the Monitoring System

Capital Investment and Financing Decisions

Master the art of designing a robust monitoring system for your projects. Explore the key steps, from defining objectives to selecting KPIs, and learn how to collect, analyze, and report data effectively. Designing an effective monitoring system is your key to project success and informed decision-making.

Potential Appraisal: Identifying and Nurturing Future Leaders

Human Resource Management

Unlocking the future leadership potential within your organization is key to sustained success. Explore the concept of potential appraisal, its methods, and how it shapes tomorrow’s leaders.

Classification of Grievances

Industrial and Employment Relations

Explore the classification of grievances in the workplace based on different criteria. Understand the categories, including individual grievances, collective grievances, systemic grievances, policy-related grievances, interpersonal grievances, and procedural grievances. Categorizing grievances helps organizations identify patterns and develop targeted solutions to address employee concerns effectively.

Comparative study of typical neural solvers in solving math word problems

Original Article
Open access
Published: 22 May 2024

Cite this article

You have full access to this open access article

Bin He ORCID: orcid.org/0000-0003-2088-8193 1 ,
Xinguo Yu 1 ,
Litian Huang 1 ,
Hao Meng 1 ,
Guanghua Liang 1 &
Shengnan Chen 1

In recent years, there has been a significant increase in the design of neural network models for solving math word problems (MWPs). These neural solvers have been designed with various architectures and evaluated on diverse datasets, posing challenges in fair and effective performance evaluation. This paper presents a comparative study of representative neural solvers, aiming to elucidate their technical features and performance variations in solving different types of MWPs. Firstly, an in-depth technical analysis is conducted from the initial deep neural solver DNS to the state-of-the-art GPT-4. To enhance the technical analysis, a unified framework is introduced, which comprises highly reusable modules decoupled from existing MWP solvers. Subsequently, a testbed is established to conveniently reproduce existing solvers and develop new solvers by combing these reusable modules, and finely regrouped datasets are provided to facilitate the comparative evaluation of the designed solvers. Then, comprehensive testing is conducted and detailed results for eight representative MWP solvers on five finely regrouped datasets are reported. The comparative analysis yields several key findings: (1) Pre-trained language model-based solvers demonstrate significant accuracy advantages across nearly all datasets, although they suffer from limitations in math equation calculation. (2) Models integrated with tree decoders exhibit strong performance in generating complex math equations. (3) Identifying and appropriately representing implicit knowledge hidden in problem texts is crucial for improving the accuracy of math equation generation. Finally, the paper also discusses the major technical challenges and potential research directions in this field. The insights gained from this analysis offer valuable guidance for future research, model development, and performance optimization in the field of math word problem solving.

Avoid common mistakes on your manuscript.

Introduction

Math Word Problem (MWP) solving has been a long-standing research problem in the field of artificial intelligence [ 1 ]. However, previous methods required hand-crafted features, making them less effective for general problem-solving. In a milestone contribution, Wang et al. [ 2 ] designed the first deep learning-based algorithm, DNS, to solve MWPs, eliminating the need for hand-crafted features. Since then, multiple neural solvers with various network cells and architectures have emerged [ 3 , 4 , 5 , 6 , 7 , 8 , 9 ], with pioneering experiments conducted on diverse datasets with varying sizes and characteristics [ 1 , 10 ]. However, the experimental results show that even MWP solvers built with similar architectures exhibit varying performance on datasets with different characteristics. Hence, a precise and impartial analysis of the existing MWP solvers has become essential to reveal the potential factors of network cells and architectures that affect the performance of neural solvers in solving different characteristics of MWPs.

Earlier MWP solvers leveraged manually designed rules or semantic parsing to map problem text into math equations, followed by an equation solver to obtain the final answer. These early efforts could only solve a limited number of problems defined in advance. Inspired by deep learning models for natural language processing [ 11 , 12 ], recent neural solvers use an Encoder-Decoder framework [ 13 ] to transform a sequence of problem sentences into another sequence of arithmetic expressions or equations. The Encoder captures the information presented by the problem text, which can be divided into two categories: sequence-based representation learning [ 5 , 14 , 15 ] and graph-based representation learning [ 6 , 16 , 17 ]. Sequence-based representation learning processes the problem text as a sequence of tokens using recurrent neural networks [ 18 , 19 ] or transformers [ 11 ], while graph-based representation learning constructs a graph from the problem text. Graph neural networks (e.g., graph transformer model [ 20 ], inductive graph learning model [ 21 ]) are then used to learn a representation for the entire graph. Mathematical expressions can be viewed as sequences of symbols or modeled as trees based on their syntactic structure, allowing Decoders to predict output expressions based on the encoding vectors produced by the encoder. By combining different types of encoders and decoders, diverse architectures of MWP solvers have been developed, including Seq2Seq-based solvers, Seq2Tree-based solvers, and Graph2Tree-based solvers.

Several reviews and surveys have been conducted to examine the progress of research in this field. For example, Mukherjee et al. [ 22 ] made a first attempt to analyze mathematical problems solving systems and approaches according to different disciplines. Zhang et al. [ 1 ] classified and analyzed different representation learning methods according to technical characteristics. Meadows et al. [ 23 ] and Lu et al. [ 24 ] conducted a literature review on the recent deep learning-based models for solving math word problems. Lan et al. [ 10 ] established a unified algorithm test platform and conducted comparative experiments on typical neural solvers. While these reviews provide valuable insights into the field of automatic math word problem solving, little comparative evaluation has been carried out to reveal the performance variations of neural solvers with different architectures in solving various types of MWPs. An initial attempt can be found in [ 10 ] which provides a collection of experimental results of the typical neural solvers on several datasets. However, no other attempts to explore the performance variations of neural solvers with different architectures in solving different types of math word problems.

While significant efforts have been made, there remains a lack of comprehensive technical analysis to compare different network structures and their impacts on final performance. This paper presents a comparative study of typical neural solvers to unveil their technical features and performance variations in solving MWPs with diverse characteristics. We initially identify the architectures of typical neural solvers, rigorously analyzing the framework of each category, notably: Seq2Seq [ 2 , 4 ], Seq2Tree [ 5 , 25 ], Graph2Tree [ 6 , 17 ] and PLM-based models [ 26 , 27 , 28 , 29 , 30 ]. We propose a four-dimensional indicator to categorize the considered datasets for precise evaluation of neural solvers’ performance in solving various characteristics of MWPs. Typical neural solvers are disassembled into highly reusable components, enabling researchers to reconstruct them and develop new solvers by replacing components with proposed ones, which benefits both model evaluation and extension. To assess the considered solvers, we establish a testbed and conduct comprehensive experiments on five popular datasets using eight representative MWP solvers, followed by a comparative analysis of the results achieved. The contributions of our work can be summarized as follows:

We provide a comprehensive and systematic analysis of deep learning-based MWP solvers, ranging from the initial deep neural solver DNS to the latest GPT-4. This is achieved through an in-depth technical analysis of network structures and neural cell types, enabling a deeper understanding of the technological evolution of MWP solvers for the research community.

To enhance the technical analysis, we introduce a unified framework consisting of reusable encoding and decoding modules decoupled from existing MWP solvers. This framework allows for the straightforward reproduction and extension of typical MWP solvers by combining these reusable modules.

We establish a testbed and provide finely regrouped datasets to facilitate objective and fair evaluations of MWP solvers. Through this testbed, we conduct comprehensive testing and report detailed results for eight representative MWP solvers on five finely regrouped datasets, specifically highlighting the performance variations of solvers with different modules in solving different types of MWPs.

We present three key findings from our experiments and discuss the major technical challenges and potential research directions in this field.

The rest of the paper is organized as follows: Sect. “ Related work ” describes related work on math word problem solving. Section “ Architecture and technical feature analysis of neural solvers ” provides a detailed analysis of the framework of typical neural solvers. A characteristic analysis of the considered datasets is presented in Sect. “ Characteristics analysis of benchmark datasets ”, and experiments and a comparative analysis are conducted in Sect. “ Experiment ”. We conclude this paper in Sect. “ Conclusion ”.

Related work

In this section, we will explore various deep learning-based approaches for solving math word problems. We will also provide an introduction to previous surveys in this field.

Deep learning-based approaches for solving MWPs

Solving MWPs has been a longstanding research focus in the field of artificial intelligence since the 1960s, as illustrated in Fig. 1 . The evolution of MWP solvers can be categorized into different stages based on the underlying technologies utilized, including rule-based approaches [ 31 ], semantic parsing-based approaches [ 16 , 32 , 33 , 34 ], etc.. More recently, neural networks inspired by deep learning models for natural language processing [ 11 , 12 ] have been designed to tackle MWPs. For instance, the Deep Neural Solver (DNS) [ 2 ] is the first deep learning algorithm capable of translating problem texts to equations without relying on manually-crafted features. This advantage has motivated extensive research on neural solvers using larger datasets, as evidenced by several studies in the literature.

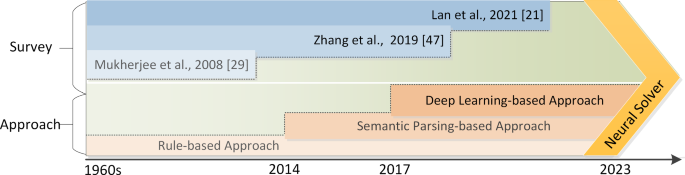
Approach evolution in solving MWPs

A significant challenge in these studies is efficiently capturing the logical relationships between natural language texts and their corresponding equations [ 1 ] which is known as problem text representation and equation representation. Inspired by translation models [ 19 ], MWP solver is typically designed as an Encoder-Decoder framework [ 1 ] as shown in Table 1 . The Encoder is responsible for learning the semantic representation and logic relationships presented explicitly or implicitly of the problem text. Researchers have tried different sequence models, leading to several representative models such as DNS [ 2 ], MathEN [ 4 ]. The Decoder, usually designed as a sequence or tree structural model, treats the math equation as a symbolic sequence consisting of numbers and operators for decoding. Several tree-structured models, such as Tree-Dec [ 25 ], GTS [ 6 ], were designed and then widely accepted for math equation decoding to enhance the math equation generation. Recently, encoder-only pre-trained models like BERT [ 35 ] and GPT [ 28 , 29 ], were included in MWP solvers to effectively represent background knowledge. In the subsequent sections, we will provide a comprehensive review from these three perspectives.

Problem text representation

To avoid sophisticated feature engineering, deep learning technologies were applied for problem text representation. In this field, Wang et al. [ 2 ] have made significant contributions by designing a customized model called Deep Neural Solver (DNS) to automatically solve MWPs. Within the DNS, the problem text and mathematical expressions are represented as sequential data, making them amenable to processing by sequence models commonly used in Natural Language Processing (NLP). Consequently, the task of solving mathematical problems is modeled as a “translation" problem within a Sequence-to-Sequence (Seq2Seq) framework. Following this pioneering work, a number of Seq2Seq models [ 4 , 5 , 13 , 36 , 37 ] for MWPs have been developed. These Seq2Seq models treat the problem text as a sequence of word tokens and utilize Recurrent Neural Networks (RNNs) such as Long-Short Term Memory (LSTM) network [ 3 ], Gated Recurrent Unit (GRU) [ 47 ], and Transformer [ 11 ] for encoding the word sequence.

To enhance the representation of the problem text, numerous optimization strategies and auxiliary techniques have been proposed. For instance, Wang et al. [ 4 ] utilized different deep neural networks for problem encoding and achieved higher accuracy compared to other Seq2Seq models. Shen et al. [ 33 ] employed a multi-head attention mechanism to capture both local and global features of the problem text. Li et al. [ 37 ] developed a group attention mechanism to extract diverse features pertaining to quantities and questions in MWPs. These efforts aim to better capture the contextual information in the problem text, thereby improving the efficiency of expression generation.

In addition to capturing the contextual information from the problem text, researchers have explored graph-based models inspired by the success of previous works [ 20 , 21 ] to capture non-sequential information, such as quantity unit relations, numerical magnitude relations, and syntactic dependency relations. These non-sequential relations are considered helpful in ensuring the logical correctness of expression generations. For instance, quantity unit relationships can help reduce illegal operations between values with different units, and numerical magnitude relationships can help reduce the occurrence of negative results from subtracting a larger number from a smaller number. Based on these assumptions, Zhang et al. propose Graph2Tree [ 6 ], which constructs a quantity cell graph and a quantity comparison graph to represent quantity unit relationships and numerical magnitude relationships, respectively. Similarly, Li et al. [ 17 ] introduce the constituency tree augmented text graph, which incorporates a constructed graph into a graph neural network [ 48 , 49 ] for encoding. The output of these graph models, combined with the output of the sequence model, is used for decoding. Additionally, knowledge-aware models [ 7 , 50 , 51 ] have been designed to improve problem representation.

Recently, Pre-trained Language Models (PLMs), and especially transformer-based language models, have shown to contain commonsense and factual knowledge [ 52 , 53 ]. To enhance the representation of problem texts, PLMs were employed for problem text encoding, aiming to reason through outside knowledge provided by the PLMs. Yu et al. [ 40 ] utilized RoBERTa [ 54 ] to capture implicit knowledge representations in input problem texts. Li et al. [ 41 ] leveraged BERT [ 35 , 55 ] for both understanding semantic patterns and representing linguistic knowledge. Liang et al. [ 26 ] employed BERT and RoBERTa for contextual number representation. These models have yielded significant improvement in terms of answer accuracy. Recently, decode-only PLMs, such GPT [ 28 ], PaLM [ 44 , 45 ] and LLaMA [ 46 ], exhibit strong reasoning abilities and their potential in solving MWPs, especially integrated with technologies of prompt [ 56 ] and chain-of-thought [ 57 ]. For instance, the latest release, GPT4-CSV [ 30 ], achieved an almost 20% increase in answer accuracy on the MATH dataset compared to GPT3.5 [ 28 ]. However, despite these improvements, issues such as actual errors and reasoning errors [ 58 ] by LLMs may lead to wrong answers even with carefully crafted prompt sequences.

Math equation representation

The representation of math equations presents another challenge in the design of MWP solvers. Initially, math equations were commonly modeled as sequences of symbols and operators, known as equation templates [ 2 ]. This allowed for direct processing by sequence models such as LSTM, GRU, etc. However, these sequence models suffer non-deterministic transduction [ 1 , 4 ] as a math word problem can have multiple correct equations. To address this issue, approaches such as MathEN [ 4 ] was proposed to normalize the duplicated equations to ensure that each problem text corresponds to a unique math equation. Chiang et al. [ 13 ] took it further by utilizing the Universal Expression Tree (UET) to represent math equations. However, these methods encode math equations using sequence models, ignoring the hierarchical structure of logical forms within math equations.

To capture the structural information, researchers have proposed tree-structured models (TreeDecoders) [ 5 , 17 , 25 ] for the iterative construction of equation trees. Liu et al. [ 25 ] developed a top-down hierarchical tree-structured decoder (Tree-Dec) inspired by Dong et al. [ 59 ]. The Tree-Dec [ 25 ] enhances a basic sequence-based LSTM decoder by incorporating tree-based information as input. This information consists of three components: parent feeding, sibling feeding, and previous token feeding, which are then processed by a global attention network. Xie et al. [ 5 ] introduced a goal-driven mechanism (GTS) for feeding tree-based information. Li et al. [ 17 ] applied a separate attention mechanism to the node representations corresponding to different node types. Additionally, Zhang et al. [ 27 ] proposed a multi-view reasoning approach that combines the top-down decomposition of TreeDecoder with the bottom-up construction of reductive reasoning [ 9 ]. Due to its exceptional ability in math equations generation, TreeDecoders has been widely adopted by subsequent MWP solvers [ 7 , 38 , 39 , 43 , 60 ]. Furthermore, several extensions of TreeDecoders have been explored, such as the generation of diverse and interpretable solutions [ 7 , 38 , 39 , 60 ].

The previous survey work

Despite the extensive research conducted in the field of MWP solving, there is a lack of comprehensive reviews. Mukherjee et al. [ 22 ] conducted a functional review of various natural language mathematical problem solvers, starting from early systems like STUDENT [ 61 ] to lately developed ROBUST [ 62 ]. The paper provides a systematic review of representative systems in domains such as math problems, physics problems, chemistry problems, and theorem proving. It highlights that these systems are generally useful for typical cases but have limitations in understanding and representing problems of diverse nature [ 22 ]. Additionally, there is a lack of unified benchmark datasets and clear evaluation strategies. However, since the publication date of the paper is early, it does not cover the current mainstream neural network-based methods, which limits its comprehensive assessment of the research field.

With the rise of machine learning-based MWP solving, Zhang et al. [ 1 ] conducted a review of these emerging works from the perspective of representation of problem texts and mathematical expressions. The paper categorizes the development of machine-answering techniques into three stages: rule-based matching, statistical learning and semantic parsing, and deep learning. The authors argue that the primary challenge in machine answering is the existence of a significant semantic gap between human-readable words and machine-understandable logic. They focus on reviewing tree-based methods [ 16 , 63 , 64 , 65 ] and deep learning-based methods [ 32 , 66 , 67 , 68 , 69 ]. The paper also reports the test results of these methods on certain datasets, aiming to provide readers with insights into the technical characteristics and classification of machine answering in the era of machine learning.

In recent literature, Meadows et al. [ 23 ] and Lu et al. [ 24 ] conducted comprehensive surveys on the emerging deep learning-based models developed for solving math word problems. These studies systematically classify and document the network architectures and training techniques utilized by these models. Furthermore, they provide a detailed analysis of the challenges faced in this field as well as the trends observed in the development of such models. Lan et al. [ 10 ] developed MWPToolkit, a unified framework and re-implementation of typical neural solvers [ 2 , 4 , 5 , 6 , 13 , 19 , 33 , 36 , 37 , 38 ]. MWPToolkit provides specified interfaces for running existing models and developing new models. However, there is a lack of technical analysis on the network structures of these neural solvers. Recently, pilot work has been conducted to compare the performance of MWP solvers based on deep learning models. Chen et al. [ 70 ] performed a comparative analysis of six representative MWP solvers to reveal their solving performance differences. Building upon this prior work, He et al. [ 71 ] further investigated the performance comparison of representation learning models in several considered MWP solvers.

This paper conducts an in-depth and comprehensive comparative analysis to reveal the technical features and performance variations of typical neural solvers when solving MWPs with different characteristics. The goal is to assist researchers in selecting more effective network units and structures for tasks with different features.

Architecture and technical feature analysis of neural solvers

The general architecture of neural solvers.

Math word problem solving is a mixed process of reasoning and calculating that can hardly be solved directly by neural networks that are designed for classification or regression tasks. Hence, most of the neural solvers take a two-step solution of expression generation and answer calculation. The former aims to translate the input problem text into a calculable math expression and then be followed by a mathematical solver to calculate the final answer. Therefore, the key challenge of solving a math word problem is to generate the target math expression.

Earlier solvers, such as DNS [ 2 ], tackle this challenge by using a seq2seq model in which math expressions are abstracted into expression templates and each template is treated as a sequence with operators and symbols. Later, to improve the capability of new expression generation, math expressions are modeled as decomposable tree structures instead of fixed structures of sequences. A milestone work of tree-structured decomposing is the Graph2Tree model proposed by Xie et al. [ 5 ] and this model is widely used in the newly developed neural solvers. Under this Graph2Tree model, the math expression generation is further divided into three sub-steps, including problem modeling, problem encoding and expression decoding as shown in Fig. 2 .

The general architecture of a neural solver for solving math word problems

Generally, a neural solver can be summarized as an Encoder-Decoder architecture of

where the problem P is consisted by a word token sequence $V=(v_1, v_2,...,v_n)$ and each $w_i$ denotes the token of word $w_i$ . $F_{encoding}(.)$ and $F_{decoding}(.)$ are networks to obtain the problem text representation and generate math equations accordingly. The goal of building a neural solver is to train an encoding network $F_{encoding}(.)$ for problem feather representation learning, and a decoding network $F_{decoding}(.)$ for predicting math expressions $ME=(e_1,e_2,...,e_m)$ to achieve the final answer. We give a detailed analysis of the architecture of mainstream encoders and decoders below separately.

Problem modeling. Problem modeling defines the pipeline of neural networks. Specifically, it models the data structure of the input and output of the solvers. For input, the problem texts are usually modeled as word sequences followed by a recursive neural network for feature learning. A huge improved work has been made which converts sequential texts into graphs, hence graph neural networks can be used for feature learning.

The output of the solvers is the target math expression which can be modeled as specially designed sequences composed of operators and number tokens. An expression vocabulary is defined which contains operators (e.g., $+,-,\times , \div $ ), constant quantities (e.g., $ 1, \pi $ ) and numbers presented by the problem text. Based on the built vocabulary, a math expression can be abstracted as an expression template in which digits are replaced by number tokens of $n_i$ . In recent works, target expressions are represented as expression trees. A basic expression tree contains three nodes of the root, left child and right child. The child node can be a digit or an operator that owns at most two children. By employing this tree-structured decomposing, nearly all types of expressions, even those that did not exist in the training set, can also be constructed.

Problem encoding. Problem encoding is a representation learning module to learn the features from the input problem text. According to the representation learning methods applied, problem encoding can be divided into sequence-based methods and graph-based methods.

Expression decoding. Expression decoding is to train a decoding network to convert features obtained in problem encoding into expression templates. As discussed in Problem Modeling , the expression templates can be number token sequences or trees. Hence, expression decoding can be accordingly divided into sequence-based decoding methods and tree-structured decoding methods.

Answer calculation. A number mapping operation is implemented in the stage of answer calculation after expression templates are obtained by replacing the number tokens $n_i$ back to digits, followed by a mathematical solver to calculate the final answer.

Currently, neural solvers are designed as an Encoder-Decoder framework to accomplish the tasks of problem encoding and expression decoding. The early encoder-decoder model refers to Seq2Seq [ 2 ], that is, the Encoder takes the input problem text as a sequence, and the output expression predicted by the Decoder is also a sequence [ 65 ]. Later, researchers pointed out that the output expression can be better described as a tree structure, e.g. expression tree [ 72 ], equation tree [ 25 ], so the Seq2Tree model was proposed. The GTS, a typical Seq2Tree-based model, was proposed by Xie et al. [ 5 ], in which the output expressions are transformed as pre-order trees and a goal-driven decomposition method is proposed to generate the expression tree based on the input sequence Furthermore, several works revealed that a math word problem is not only a sequence, but also contains structured information about numeric quantities. To represent the quantity relationships, the graph structure is applied to model the quantities as nodes and relations as edges. By combining with tree-structural decoders, several Graph2Tree-based models are proposed [ 6 , 33 ] recently.

According to the network components applied in problem encoding ( Encoder ) and expression decoding ( Decoder ), neural network-based MWP solvers can be divided into four major categories: Seq2Seq, Seq2Tree, Graph2Tree and PLM-based model as shown in Table 2 .

Seq2Seq is a sequence-to-sequence framework, where both the Encoder and Decoder are sequence-based networks. The Encoder takes the sequence of word tokens as input and outputs the feature vectors, usually an embedding vector and a hidden state vector. The feature vectors are sent to the Decoder to predict the expression templates. The embedding vector is usually used to predict the current character of operators or number tokens and the hidden state vector records the contextual features of the current character. LSTM [ 3 ] and GRU [ 47 ] are two commonly used networks in building Encoders and Decoders [ 2 , 5 , 37 , 38 , 65 ]. For example, MathEN [ 65 ] leverages two LSTM networks as Encoder and Decoder , while DNS [ 2 ] employs an LSTM network and a GRU network as Encoder and Decoder separately.

Seq2Tree is an improved framework based on the Seq2Seq architecture in which the sequence-based Decoder is replaced by a tree-structured network to generate expression trees. As discussed above, the tree-structured network is a compound of prediction networks and feature networks, as well as a decision mechanism. For instance, in GTS [ 5 ], a prediction network and two feature networks are employed to merge the previous state vectors and to calculate the current state vector. In another work [ 17 ], only one feather network is used to accomplish the task of feature merging and calculation.

Graph2Tree combines the advantages of a graph-based encoder and a tree-based decoder in the process of problem encoding and expression decoding. Compared to Seq2Tree, Graph2Tree applies graphs to represent the structural relations among word tokens and digits into a network structure (e.g., graph) to enhance the feature learning during the problem encoding. Various kinds of algorithms have been proposed to construct graphs [ 6 , 7 , 17 , 39 ] by modeling the structural relations on both word token level and sentence level.

PLM-based models leverage pre-trained language models to generate intermediate MWP representation and solution. Depending on the type of PLM [ 58 ], there are two specific implementations of PLM-based models. The first implementation, represented by encoder-only PLMs like BERT [ 26 , 27 ], utilizes the PLM as an encoder to obtain the latent representation of the math word problem. This representation is then fed into a decoder, such as a Tree-based decoder, to generate the final mathematical expression. The second implementation, represented by models like GPT [ 28 , 29 , 30 ], directly employs Transformer networks for mathematical reasoning, producing the desired results without an explicit separation between encoding and decoding stages. This approach streamlines the process and enhances the efficiency of solving math word problems.

As shown in Table 2 , DNS and MahtEN are Seq2Seq models, while GTS is built as a seq2tree structure. The tree-structured decoder designed in GTS is also applied in Graph2Tree $^1$ . Graph2Tree $^1$ and Graph2Tree $^2$ are two graph2tree models but differ in both graph encoding and tree decoding. In the stage of graph encoding, Graph2Tree $^1$ uses Quantity Cell Graph and Quantity Comparison Graph to describe the quantity relationships, while Graph2Tree $^2$ leverages Syntactic Graph to present the word dependency and the phrase structure information. In the decoding stage, a pre-order expression tree is generated in Graph2Tree $^1$ , while Graph2Tree $^2$ employs a hierarchical expression tree to model the output expression.

Problem text encoding

In recent years, a trend in building MWP solvers [ 1 ] is to apply deep neural networks to capture the quantity relationships presented by problem texts explicitly and implicitly. The early MWP solvers [ 2 , 65 ] mainly use sequence-based models, such as LSTM [ 3 ], GRU [ 47 ], etc., to conduct problem representation learning, in which the problem text is regarded as an unstructured sequence. Recently, graph-based representation learning methods [ 5 , 6 , 17 ] are widely employed to enhance both structured and unstructured information learning, which attracts more and more attention of community researchers. On the other hand, several benchmark datasets with diverse characteristics were released for performance evaluation of the proposed solvers [ 10 ]. To reveal the potential effectiveness of presentation learning methods on diverse characteristics of MWPs, a comparative analysis of sequence-based and graph-based representation learning is conducted in this paper.

Sequence-based problem encoding

As a problem is mainly presented by natural language text, the sequence-based recursive neural network (RNN) models [ 3 , 47 ] are naturally taken to problem representation learning. For example, DNS [ 2 ] uses a typical Seq2Seq model for problem representation learning, where words are split into tokens inputted into a GRU module to capture quantity relations. Several follow-up works were proposed by replacing GRU with BiLSTM or BiGRU to enhance the ability of quantity relation learning [ 7 , 14 , 15 ]. To improve the semantic embedding, pre-trained language models, such as GloVe [ 17 ], BERT [ 26 ], Chinese BERT [ 55 ] and GPT [ 28 , 73 ], etc., were used to better understand the input problem texts. Besides, to capture more features between problem sentences and the goal, attention modules are employed in several works to extract local and global information. For instance, Li et al. [ 37 ] introduced a group attention that contains different attention mechanisms which achieved substantially better accuracy than baseline methods.

In a sequence-based representation learning model, every word of the problem text P is first transformed into the context representation. Given an input problem text $P=\{ w_{1},w_{2},...,w_{n} \}$ , each word token $w_{i}$ is vectorized into the word embedding $w_{i}$ through word embedding techniques such as GloVe [ 17 ], BERT[ 26 ], etc. To capture the word dependency and learn the representation of each token, the sequence of word embeddings is input into the RNN whose cells can be LSTM [ 3 ], GRU [ 47 ], etc. Formally, each word embedding $w_{i}$ of the sequence $E=\{ w_{1},w_{2},...,w_{n} \}$ is input into the RNN one by one, and a sequence of hidden states is produced as the output.

For unidirectional encoding, the procedure of problem representation learning can be described as follows:

where ${RNN}(\cdot ,\cdot )$ denotes a recursive neural network, $h_{i-1}^p$ denotes the previous hidden state and $w_{i}$ denotes the current input. Repeat the above calculation from step 1 to n to obtain the final hidden state $h_{n}$ , which is the result of the sequence-based representation learning. In practice, ${RNN}(\cdot ,\cdot )$ is usually specified as a two-layer LSTM or GRU network.

For bi-direction encoding, BiLSTM or BiGRU is applied to obtain the left vector $\overrightarrow{h_i^p}$ and the right vector $\overleftarrow{h_i^p}$ separately. Finally, the output hidden state $h_i^p$ is calculated as follows:

To capture different types of features in hidden state $h_s^p$ , attention mechanisms are employed to enhance the related features. For example, Li et at. [ 37 ] applied a multi-head attention network following a BiLSTM network. The output of the group attention $h_a^p$ is produced by:

where Q , K and V denote the query matrix, key matrix and value matrix separately, which are all initialized as $h_i^p$ .

The above process can be replaced by employing a pre-trained language model. As shown in Eq. 5 , a pre-trained language model PLM (.) is used to directly map the problem text, denoted as X, to a representation matrix H.

Graph-based problem encoding

To improve structural information learning, graph-based encoders were applied to represent relationships among numbers, words and sentences, etc. The structural information includes token-level information and sentence-level information. The former is also considered as local information which is constructed from the number comparison relationship (e.g., bigger, smaller), neighborhood relationship between numbers and the associated word tokens, etc. For example (as shown in Fig. 3 a), Zhang et al. [ 6 ] applied two graphs, including a quantity comparison graph and a quantity cell graph to enrich the information between related quantities. The sentence-level information, in a sense, is the global information that connects local token-level information. A commonly used sentence-level information is the syntactic structure information generated from dependency parsing. As shown in Fig. 3 b, to capture the sentence structure information, the dependency parsing and the constituency analysis [ 17 ] were applied to construct graphs. Furthermore, Wu et al. [ 50 ] proposed a mixed graph, called an edge-labeled graph, to establish the relationship between nodes at both the sentence level and problem level. Once the problem text is represented as a graph, graph networks such as GraphSAGE [ 21 ], GCN [ 74 ], can be used to learn the node embedding. One of the advantages of using graph representation learning is that external knowledge can be easily imported into the graph to improve the accuracy of problem solving [ 50 ].

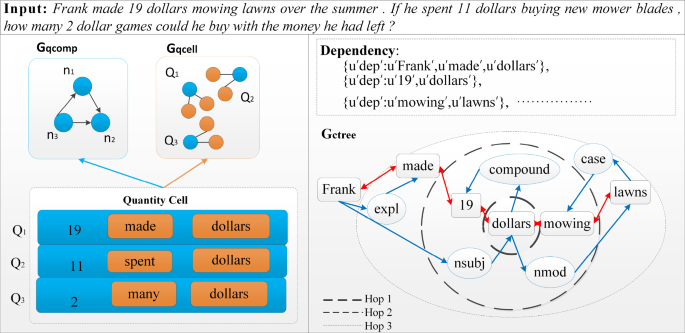
Comparison of graph-based quantity relation representation. a Quantity comparison graph and quantity cell graph designed by Zhang et al. [ 6 ]; b Constituency tree augmented text graph applied by Li et al. [ 17 ]

Different from the sequence-based representation learning methods, the graph-based representation learning methods take important structural information into consideration when encoding. Due to the fact that different researchers construct the graph using different methods, unifying these methods is more complex than unifying the sequence-based representation learning methods. Through the summary and induction of several typical works[ 6 , 7 , 16 , 17 ], we divide the procedure of sequence-based representation learning into three steps: node initialization, graph construction and graph encoding.

Graph Construction. The graph construction is a pre-process before graph encoding, which converts the problem P into a graph $G=(V, E)$ aiming at preserving more structural information hidden in P . To this end, elements such as words and quantities are treated as nodes V , and syntactic relationships such as grammatical dependency and phrase structure are modeled as edges E .

To enrich the information during graph construction, several adjacency modeling approaches are proposed to construct graphs according to the relationships of words and numbers in P . For example, in reference [ 16 ], a Unit Dependency Graph (UDG) is constructed to represent the relationship between the numbers and the question being asked. In work [ 6 ], two graphs, including a quantity comparison graph and a quantity cell graph, are built to model the relationships between the descriptive words associated with a quantity. Syntactic constituency information is used to construct the quantity graph in [ 17 ]. Through the graph construction process, a set of graph $\mathbb {G} =\{ G_1,G_2,...,G_K \}$ is obtained from problem P for graph encoding.

Graph encoding. After initializing the node and constructing the graph, the graph neural network is applied to obtain the output vector. The procedure can be summarized as follows:

where $G\!N\!N(\cdot ,\cdot )$ denotes a graph neural network, such as GCN [ 74 ] or GraphSAGE [ 21 ]. The pair $(E_k,V_k)$ represents the $k_{th}$ graph $G_k$ in $\mathbb {G}$ , with $V_k$ as the node set and $E_k$ as the edge set. Both $V_k$ and $E_k$ are formed during the node initialization stage. $h_k^g$ denotes the hidden state corresponding to the input graph $G_k$ . When more than one graph ( $k>1$ ) is utilized, the output values ${h_k^g}_{k=1}^K$ are concatenated and projected to produce the final value H . Finally, the global graph representation $h^g$ can be obtained:

where $FC(\cdot )$ is a fully connected network and $Pooling(\cdot )$ denotes pooling function.

Math expression decoding

To achieve the final answer, vectors after problem representation learning are decoded as mathematical expressions followed by a math solver to calculate the answer. Early neural solvers, such as DNS [ 2 ], employ a typical Seq2Seq model to predict mathematical expressions. Later, to improve the generation ability of new expressions, tree-based models [ 5 ] are proposed to capture the structure information hidden in expressions.

Expression Decoder decodes the feature vectors obtained by the problem Encoder into expression templates. The decoding process is a step-by-step prediction of number tokens and operators. Therefore, recursive neural networks are naturally chosen for this task. The decoding process can be described as a conditional probability function as follows:

where x denotes vectors of input problems, $y_t$ and $h_t$ is the predicted character and decoder hidden state at step t separately, and $F_{prediction}$ is a non-linear function. The key component of Eq. ( 8 ) is the computation of $h_t$ to ensure the output expressions are mathematically correct. Hence, the default activation functions of the general RNNs need to be redesigned. According to the redesigned activation functions, expression decoding can be divided into two main categories: sequence-based decoding and tree-based decoding.

Sequence model based expression decoding

In sequence-based models, expressions are usually abstracted as a sequence of equation templates with number tokens and operators [ 2 , 37 , 65 ]. For example, the expression $x = 5+2*3$ is described as an equation template $x=n_1+n_3+n_2$ , $n_i$ is the token of the i th number in problem P . In the stage of math expression generation, a decoder is designed to predict an equation template for each input problem and then expressions are generated by mapping the numbers in the input problem to the number tokens in the predicted equation template [ 2 ]. Hence, the math expression generation is transformed into a sequence prediction task and one of the core tasks of math expression generation is to design a decoder to predict the equation templates. Typical sequence models built for NLP tasks can be directly applied for building such decoders [ 47 , 72 ]. Compared to retrieval models [ 32 , 75 ], sequence-based models achieved significant improvement in solving problems requiring new equations that not existed in the training set. However, these models are usually sensitive to the length of the expressions as they generate solution expressions sequentially from left to right.

In sequence-based expression decoding, the activation function is defined according to the basic rules of arithmetic operations. For example in infix expressions, if $y_{t-1}$ is a number, then $y_t$ should be a non-number character. Therefore, the redesigned activation function differs according to the infix and suffix expressions used.

In infix sequence models [ 2 ], predefined rules are used to decide the type of the $t_{th}$ character according to the $(t-1)_{th}$ character. For example, rule “If $y_{t-1}$ in $\{+,-,\times , \div \}$ , then $y_t$ will not in $\{+,-,\times , \div , ),= \}$ ” defines the following character after an operator is predicted. Similar rules are used to determine characters after “(, ), =” and numbers are predicted.

In suffix sequence models [ 36 , 37 ], two numbers will be first accessed by the RNN to determine the operator and generate a new quantity as the parent node. The representation of the parent node $o_c$ can be calculated by a probability function like:

where $h_l, h_r$ are the quantity representations for the previously predicted nodes, and $W_1, W_2$ and b are trainable parameters.

Tree-structured model based expression decoding

To describe the structural relation among operators and digits, expression templates are represented as tree structures and tree-structured networks are proposed to learn the structural features of the expression trees. Compared to left-to-right sequential representation in sequence-based methods, relationships among operators and numbers are represented by tree structures, such as expression tree [ 72 ] or equation tree [ 63 ]. Strictly, the tree-structured network is not a novel network architecture but a compound of networks and a decision mechanism. For example, the previous state when predicting a left child node is the parent node state, but in a right child node prediction, both the parent node state and the left child node state are considered as the previous state [ 5 ]. Hence, a decision mechanism is designed to choose different embedding states when predicting a left and right child node. Besides, various neural cells (e.g., a prediction network and a feature network) are usually employed for current character prediction and current hidden state calculation [ 6 , 17 ].

Therefore, the tree-structured networks are decided by the structure of the expression trees and the tree-based decoding is a decomposing process of an expression tree. According to the decomposing strategy employed, tree-based decoding can be divided into two main categories: depth-first decomposing [ 5 , 6 ] and breadth-first decomposing [ 17 ].

Depth-first decomposing. As shown in Fig. 4 b, the depth-first decomposing starts from the root node and implements a pre-order operation during the prediction. As such, if an operator is predicted, then go to predict the left child until a number node is predicted, then go to predict the right child. To make full of available information, the prediction of the right child takes the information of its left sibling node and the parent information into consideration. Roy et al. [ 72 ] proposed the first approach that leverages expression trees to represent expressions. Xie et al. [ 5 ] proposed a goal-driven tree-structured neural network, which was adopted by a set of latter methods [ 6 , 14 , 15 ], to generate an expression tree.

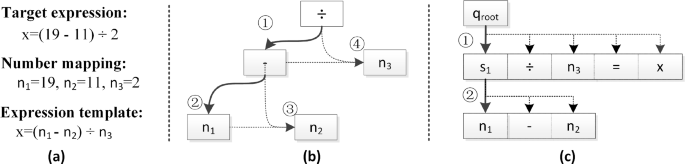
An example of tree-structured decomposing. a Input expression template; b Depth-first decomposing; c Breadth-first decomposing

Breadth-first decomposing. In breadth-first decomposing models, expressions are represented as hierarchically connected coarse equations. A coarse equation is an algebraic expression that contains both numbers and unknown variables. Compared to depth-first decomposing, an essential difference of breadth-first decomposing is that the non-leaf nodes are specified as variables. Therefore, the variable nodes are decomposable nodes that can be replaced by sub-trees. As shown in Fig. 4 (c), an example equation is firstly represented as a 1st-level coarse equation $s_1 \div n_3(2)=x$ containing a non-leaf node $s_1$ and four leaf nodes. Then, the non-leaf node $s_1$ is decomposed into a sub-tree as the 2nd-level coarse equation of $n_1(19)-n_2(11)$ . When all coarse equations are achieved then go to predict the 3rd-level coarse equations if it has, otherwise, the decomposing stops.

To start a tree generation process, the root node vector $q_{root}$ is initialized according to the global problem representation. For each token y in the target word $V^{dec}$ , the representation for a certain token $\textrm{e}(y \mid P)$ , as denoted as $h_t$ in Eq. ( 8 ), is defined as follows:

where $\textrm{e}_{(y, op)}$ , $\textrm{e}_{(y,u)}$ and $\textrm{e}_{(y, con)}$ denotes the representation of operators, unknowns and quantities separately that is obtained from 3 independent embedding matrices $M_{op}$ , $M_{unk}$ and $M_{con}$ . $\bar{h}_{loc(y, P)}^{p}$ is the quantity representation from Eqs. ( 3 ) or ( 4 ). $V^{dec}$ is the target vocabulary which consists of 4 parts: math operators $V_{op}$ , unknowns $V_u$ , constants $V_{con}$ and the numbers $n_p$ .

In order to adapt to the tree-structured expression generation, activation functions are redesigned according to the types of nodes in the expression tree. The nodes are categorized into two types: leaf nodes and non-leaf nodes. When a non-leaf node is predicted, further decomposing is needed to predict the child nodes. Otherwise, stop the current decomposing and go to predict the right child nodes. The non-leaf node differs in different representations of tree-structured expressions. In regular expression trees [ 5 , 6 ], the non-leaf nodes are operators while numbers are treated as leaf nodes. While in a heterogeneous expression tree, the non-leaf nodes are non-target variables that are represented by sub-expressions.

Based on the above discussion, the whole procedure of tree-based expression decoding can be summarized as follows [ 5 , 6 , 7 , 14 ]:

1) Tree initialization: Initialize the root tree node with the global embedding $H_g$ and perform the first level decoding:

where the global embedding $H_g$ is the original output of the problem Encoder .

2) Left sub-node generation: A sub-decoder is applied to derive the left sub-node. The new left child $n_l$ is conditioned on the parent node $n_p$ and the global embedding $H_g$ . The token $\hat{y}_l$ is predicted when generating the new left node:

If the generated $\hat{y}_l \in V_{op}$ or $\hat{y}_l \in V_{u}$ , repeat step 2). If the generated $\hat{y}_l \in V_{con}$ or $\hat{y}_l \in n_p$ , get into step 3).

3) Right-node generation: Different from the left sub-node generation, the right sub-node is conditioned on the left sub-node $n_l$ , the global embedding $H_g$ and a sub-tree embedding $t_l$ . The right sub-node $n_r$ and the corresponding token $\hat{y}_r$ can be obtained as:

where the sub-tree embedding $t_l$ is conditioned on the left sub-node token $\hat{y}_l$ and left sub-node $n_l$ . If the $\hat{y}_r \in V_{op}$ or $\hat{y}_r \in V_{u}$ , repeat step 2). If the generated $\hat{y}_r \in V_{con}$ or $\hat{y}_r \in n_p$ , stop decomposing and backtrack to find a new empty right sub-node position. If no new empty right nodes can be found, the generation is completed. If the empty right node position still exists, go back to step 2).

In other models [ 17 ], step 2) and 3) are combined into a sub-tree generation module in which the token embedding $s_t$ and the corresponding token $\hat{y}_t$ at time t are calculated as follows:

where $st_{parent}$ stands for sub-tree node embedding from the parent layer and $st_{sibling}$ is the sentence embedding of the sibling.

Compared to earlier sequence-based decoders which are usually retrieved models, tree-based decoders are generative models that can generate new expressions not existing in the training set. The generation ability lies in the iterative process of tree-structured decomposing as defined in Eq. 10 and the equation accuracy was greatly improved by using tree-based decoders. Detailed results can be found in Sect. “ Experiment ”.

Characteristics analysis of benchmark datasets

Widely used benchmark datasets.

Problem texts and equations are two essential items for neural solver evaluation. The problem text of each example in the dataset is a natural language stated short text that presents a fact and raises a question and the equation is a math expression(s) (e.g., an arithmetic expression, an equation or equations) that can be used to generate the final answer to the question raised by the problem text. A problem text can be stated in any language but most of the widely used datasets are stated in English [ 32 , 76 , 77 ] until Wang et al. [ 2 ] released a Chinese dataset Math23K in 2017 which contains 23,161 problems with carefully labeled equations and answers. A brief introduction of the widely accepted benchmark datasets is given as follows and the result of a statistical analysis conducted on the considered datasets is shown in Table 3 .

Alg514 is a multiple-equation dataset created by Kushman et al. [ 32 ]. It contains 514 algebra word problems from Algebra.com. In the dataset, each template corresponds to at least 6 problems (T6 setting). It only contains 28 templates in total.

Draw1K is a multiple-equation dataset created by Upadhyay et al. [ 78 ]. It contains 1000 algebra word problems also crawled and filtered from Algebra.com.

Dolphin18K is a multiple-equation dataset created by Huang et al.[ 77 ]. It contains 18,711 math word problems from Yahoo! Answers with 5,738 templates. It has much more and harder problem types than the previous datasets.

MAWPS-s is a single-equation dataset created by Koncel-Kedziorski et al. [ 76 ]. It contains 3320 arithmetic problems of different complexity compiled from different websites.

SVAMP is a single-equation dataset created by Patel et al. [ 79 ]. It contains 1000 problems with grade levels up to 4. Each problem consists of one-unknown arithmetic word problems which can be solved by expressions requiring no more than two operators.

Math23K is a single-equation dataset created by Wang et al. [ 2 ]. It contains 23, 162 Chinese math word problems crawled from the Internet. Each problem is labeled with an arithmetic expression and an answer.

HMWP is a multiple-equation dataset created by Qin et al. [ 38 ]. It contains 5491 Chinese math word problems extracted from a Chinese K12 math word problem bank.

Despite the available large-scale datasets, neural solver evaluation is still a lot trickier for the various types and characteristics of math word problems. As almost all neural solvers predict equation templates directly from the input problem text, the complexity and characteristics of the equations and the input problem texts need further study to make the evaluated results more elaborate.

Characteristics analysis

To evaluate the neural solvers, three widely used benchmark datasets include two English datasets MAWPS-s and SWAMP , and a Chinese dataset Math23k . All the selected datasets are single-equation problems as almost all solvers support the single-equation generation task. Conversely, not all solvers support the multi-equation generation task which may lead to poor comparability.

As discussed in Sect. “ Characteristics analysis of benchmark datasets ”, problem texts and expressions differ greatly in terms of scope and difficulty between different datasets. In order to reveal the performance difference of neural solvers on datasets with different characteristics, the selected benchmark datasets are categorized into several sub-sets based on four-index characteristic factors of L , H , C and S defined as follows:

Expression Length ( L ): denotes the length complexity of the output expression. L can be used as an indicator of the expression generation capability of a neural solver. According to the number of operators involved in the output expression, L is defined as a three-level indicator containing $L_1$ , $L_2$ and $L_3$ . $L_1$ level: $l<T_0$ , $L_2$ level: $T_0<=l<=T_1$ , $L_3$ level: others. Where l represents the number of operators in the output expression. $T_0$ , $T_1$ denote the thresholds of l at different levels of length complexity.

Expression Tree Depth ( H ): denotes the height complexity of the output expression tree. H is another generation capability indicator, especially for tree-structured neural solvers. According to the depth of the expression tree, H is defined as a two-level indicator containing $H_1$ and $H_2$ . $H_2$ level: $h < T_2$ , $H_3$ level: others. Where h refers to the height of the expression tree, $T_2$ is a threshold.

Implicit Condition ( C ): denotes whether implicit expressions needed to solve the problem are embedded in the problem text. $C_{1}$ refers to problems with no implicit expression, while $C_{2}$ refers to problems with one or more implicit expressions. C can be used as an indicator associated with the relevant information understanding of the solver.

Arithmetic Situation ( S ): denotes the situation type that a problem belongs to. The different arithmetic situation indicates different series of arithmetic operations. Based on Mayer’s work, we divide math word problems into five typical types which are Motion ( $S_m$ ), Proportion ( $S_p$ ), Unitary ( $S_u$ ), InterestRate ( $S_{ir}$ ), and Summation ( $S_s$ ). S can be used as an indicator associated with the context understanding of the solver.

Each of the selected benchmark datasets is divided into three sub-sets of train-set (80%), valid-set (10%) and test-set (10%). These sub-sets are further characterized according to the above four indices. Tables 4 and 5 show the percentage of problems of different benchmark datasets on the four indices for training and testing separately. Compared to Math23K, expressions in MAWPS-s and SVAMP are much more simple on both factors of the expression length and expression depth. Hence, we set different thresholds for $T_i$ to generate $L_*$ and $H_*$ subsets. Moreover, implicit expression and problem situation analysis are only implemented on Math23K dataset.

Experimental setup

Selected typical neural solvers: To ensure the fairness of the performance evaluation, two representative solvers were selected from each framework as shown in Table 2 . The selected solvers are listed below:

DNS [ 2 ]: The first Seq2Seq model using a deep neural network to solve math word problems. The model combines the RNN model and the similarity-based retrieval model. If the maximum similarity score returned based on the retrieval model is higher than the specified threshold, the retrieval model is then selected. Otherwise, the Seq2Seq model is selected to solve the problem.

MathEN [ 4 ]: The ensemble model that combines three Seq2Seq models uses the equation normalization method, which normalizes repeated equation templates into expression trees.

GTS [ 5 ]: A tree-structured neural model based on the Seq2Tree framework to generate expression trees in a goal-driven manner.

SAU-Solver [ 38 ]: A semantically aligned universal tree structure solver based on the Seq2Tree framework, and it generates a universal expression tree explicitly by deciding which symbol to generate according to the generated symbols’ semantics.

Graph2Tree [ 6 , 17 ]: Graph2Tree $^1$ and Graph2Tree $^2$ are both deep learning architectures based on the Graph2tree framework, combining the advantages of a graph-based encoder and a tree-based decoder. However, the two differ in graph encoding and tree decoding.

Bert2Tree [ 26 ]: An MWP-specific large language model with 8 pre-training objectives designed to solve the number representation issue in MWP.

GPT-4 [ 30 ]: A decoder-only large language model released by OpenAI in March, 2023.

The above selected typical solvers are evaluated in solving characteristic problems on five benchmark datasets and the detailed results can be found in Sect. “ Performance on solving characteristic problems ”.

Component Decoupling According to the discussion in Sect. “ Architecture and technical feature analysis of neural solvers ”, each solver consists of an encoder which can be decomposed into one or more basic RNN or GNN cells. To identify the contribution of these various cells during the problem solving, we decouple the above considered solvers into individual components. The decoupled components can be integrated into different solvers and can be replaced by other similar components. Components decoupled from encoders are listed as follows.

LSTM Cell : A long-short term memory network derived from sequence-based encoders for non-structural problem text encoding.

GRU Cell : A gated recurrent unit derived from sequence-based encoders for non-structural problem text encoding.

BERT Cell : A pre-trained language model used to directly map the problem text into a representation matrix for generating the solution.

GCN Cell : A graph convolution network derived from graph-based encoders for structural problem text encoding.

biGraphSAGE Cell : A bidirectional graph node embedding module derived from graph-based encoders for structural problem text encoding.

The LSTM cell and GRU cell take text sequence as input and output two text vectors including an embedding vector and a hidden state vector. The GCN cell and biGraphSAGE cell take the adjacency matrix as input and output two graph vectors. Similarly, components decoupled from decoders are listed below.

DT Cell : A depth-first decomposing tree method derived from Graph2Tree $^1$ for math equation decoding. DT cell takes an embedding vector and a hidden vector as input and output a math equation.

BT Cell : A breadth-first decomposing tree method derived from Graph2Tree $^2$ for math equation decoding. The BT cell takes three vectors as input, including one embedding vector and two hidden state vectors.

Hence, a super solver is developed to reproduce the selected typical solvers and design new solvers by redefining the combination of the decoupled components. The performance of newly developed solvers are shown and discussed in Sects. “ Comparative analysis of math expression decoding models ” and “ Comparative analysis of problem encoding models ” separately.

Evaluation Metrics Math word problems used for neural solver evaluation are usually composed of problem texts, equations and answers. Neural solvers take the problem texts as input and output the expression templates which are further mapped to calculable equations [ 1 ]. These generated equations are then compared with the equations labeled in datasets for algorithm performance evaluation. Besides this equation-based evaluation, answer-based evaluation is also used in cases where multiple solutions exist. The answer-based evaluation compares the answers calculated from the generated equations with labeled answers. Several commonly used evaluation metrics are introduced below, including accuracy ( $E_{acc}$ and $A_{acc}$ ), time cost (# Time ) and minimum GPU memory capacity (# $\mathop {G\!\!-\!\!Mem}$ ).

Accuracy. Accuracy includes answer accuracy and equation accuracy. Answer accuracy [ 2 , 5 , 7 ] is perhaps the most common evaluation method. It simply involves calculating the percentage of final answers produced by the model that is correct. This is a good measure of the model’s overall performance, but it can be misleading if the dataset is unbalanced (e.g., if there are more easy problems than difficult ones). Equation accuracy [ 6 , 17 ] is another important measure, which refers to the accuracy of the solution that the model generates. This is typically calculated by comparing the output of the model to the correct solution to the problem, and determining whether they match. Evaluating both the solution accuracy and answer accuracy can give a more complete picture of the model’s performance on MWP solving tasks.

The Equation Accuracy ( $E_{acc}$ ) which is computed by measuring the exact match of predicted equations and ground-truth equations as follows:

Similarly, the Answer Accuracy ( $A_{acc}$ ) is defined as follows:

To remove extraneous parenthesis during equation matching, equations are transformed into equation trees as described in [ 17 ]. By using $E_{acc}$ , outputs with correct answers but incorrect equations are treated as unsolved cases.

Time Cost (# Time ): denotes the time required for model training. Specifically, this article refers to the time needed for the model to complete 80 iterations with a batch size of 64.

Minimum GPU Memory Capacity (# $\mathop {G\!\!-\!\!Mem}$ ): represents the minimum GPU memory capacity required for training the model. This metric is crucial for assessing the hardware requirements of model training, particularly for researchers with limited resources.

Hyper-parameters To improve the comparability of the experimental results, the hyper-parameters of the selected solvers and the decoupled cells are consistent with the original models. For example, the default LSTM and GRU cells are initialized as a two-layer network with 512 hidden units to accommodate the pre-trained word vector which usually has a dimension size of 300. In the biGraphSAGE cell, we set the maximum number of node hops K as $K = 3$ and the pooling aggregator is employed. As to the optimizer, we use Adam with an initial learning rate of 0.001, and the learning rate will be halved every 20 epochs. We set the number of epochs to 80, batch size to 64, and dropout rate to 0.5. At last, we use a beam search with beam size 5 in both the sequence-based cells and tree-based cells. To alleviate the impact of the randomness of the neural network models, we conduct each experiment 5 times with different random seeds and report the average results. All these hyper-parameters have been carefully selected to balance computational efficiency with model performance.

Experimental Environment Our models run on a server with Intel i7 CPU. The GPU card is one NVIDIA GeForceRTX 3090. Codes are implemented in Python and PyTorch 1.4.0 is used for matrix operation. We use stanfordcorenlp to perform dependency parsing and token generation for Chinese datasets.

Performance comparison

Overall performance of considered solvers.

In this section, we initially present the learning curves of all considered models (excluding GPT-4) on two representative datasets (Math23k for Chinese and MAWPS-s for English).

It is evident that overfitting occurs on the MAWPS-s dataset, as shown in Fig. 5 . After 10 iterations, the models exhibit oscillations in terms of accuracy despite having low loss values. This suggests that overfitting has occurred in this case. The limited size of the MAWPS-s dataset, which contains only around 1500 training examples, is likely insufficient for effective training of most deep neural networks. On the other hand, the situation improves on the Math23K dataset. After approximately 30 iterations, both the loss and accuracy stabilize.

We have also examined the training time required for different models. As shown in Table 6 , without considering GPT-4 and fine-tuning of BERT, all models have completed training with a batch size of 64 within 4 min (# Time ), and have reached convergence in less than 80 iterations. Similarly, we have reported the minimum GPU memory capacity (# $\mathop {G\!\!-\!\!Mem}$ ) required for training. This has been highly attractive for individual researchers as it has allowed them to quickly train the desired models locally without incurring high costs. The next step will be to evaluate the solving performance of different models.

Learning curves on different datasets. a Learning curves on MAWPS-s; b Learning curves on Math23K

We provide an overall result of the considered solvers in terms of both single-equation and multi-equation tasks. We evaluate the $E_{acc}$ and $A_{acc}$ separately. Additionally, we report the average training time (#Time(minutes per epoch)) on Math23K.The detailed results are shown in Table 6 .

As shown in Table 6 , PLM-based models exhibit superior performance in terms of $A_{acc}$ compared to other models. Specifically, without any additional prompts, GPT-4 achieves the best results on the MAWPS-s, SVAMP, and Draw1k datasets, with accuracies of 94.0%, 86.0%, and 42.1% respectively. On the other hand, BertTree performs well on the two Chinese datasets, Math23k and HMWP, with accuracies of 84.2% and 48.3% respectively. This demonstrates the significant advantage of PLM-based models, especially large-scale language modes such as GPT-4, in solving math word problems.

However, it is important to note that there is still room for improvement in the performance of all models, particularly in solving more complex math problems such as those in the Math23k, Draw1K, and HMWP datasets. There is still a considerable gap between the current performance levels and practical requirements. Additionally, traditional lightweight models also have their merits. For instance, models utilizing Tree-based decoders achieve leading performance in terms of $E_{acc}$ , with 68.0%, 72.4%, 39.8%, and 39.6% on the SVAMP, Math23K, Draw1K, and HMWP datasets respectively. This highlights the potential advantages of Tree-based decoders in representing mathematical expressions. Furthermore, the resource requirements and response efficiency of large language models like GPT are also important considerations.

Among the lightweight models, Graph2Tree models demonstrate the best results on most selected datasets, particularly for multi-equation tasks on Draw1K and HMWP. This underscores the immense potential of the graph-to-tree framework in solving math word problems. However, we observed that Graph2Tree $^2$ did not perform as well as Graph2Tree $^1$ , underscoring the significance of careful cell selection in both problem encoding and expression decoding steps. Detailed analysis can be found in Sects. “ Comparative analysis of math expression decoding models ” and “ Comparative analysis of problem encoding models ”. Surprisingly, MathEN achieved the best performance on MAWPS-s and also outperformed other solvers in terms of $E_{acc}$ on the Math23K dataset.

Based on the training time required per epoch on Math23K, we found that more complex models resulted in higher computational times, which is consistent with our general understanding. Among them, SAU-Solver and Graph2Tree $^2$ had the longest training times, ranging from 3 to 4 min, while the DNS model, which only involves sequence encoding and decoding, had the shortest training time. Graph2Tree $^1$ and GTS reported similar time costs, indicating that the added CNN unit in Graph2Tree $^1$ has a minor impact on the computation cost of the graph-to-tree framework.

Performance on solving characteristic problems

In the following comparison, we only considered single-equation tasks for performance evaluation. This is because multi-equation tasks can be easily converted into a single-equation task by adding a special token $<bridge>$ to convert the equations into a single tree or equation [ 10 ], without requiring any model modifications. Therefore, the performance of solvers on single-equation tasks is also useful for evaluating the performance of models on multi-equation tasks.

(1) Performance on solving problems indicated by expression length.

Table 7 presents the comparison results of $E_{acc}$ in solving problems with varying equation lengths. Mean Accuracy Difference (MAD), denoted as $d_{i-k}$ , is used to indicate the accuracy difference in solving problems from level $L_{i}$ to $L_{k}$ . Due to the difficulty of obtaining annotated standard arithmetic expressions for GPT models, we utilize the $A_{acc}$ as a reference instead.

As depicted in Table 7 , PLM-based models have demonstrated superior performance compared to other models. Bert2Tree, in particular, has exhibited greater stability when compared to GPT-4. Specifically, its accuracy remains relatively consistent in both $L_1$ and $L_2$ level problems, with only a slight decrease of 17.2% in the $L_3$ task. In contrast, GPT-4 experiences a significant decrease of 54.9% from $L_1$ to $L_3$ .

Graph2Tree models performed the best on SVAMP, achieving an average $E_{acc}$ of 49.0% and 68.0%, respectively. Graph2Tree $^1$ proved better at solving long equation problems. For example, on Math23k, it achieved state-of-the-art performance of 73.8% and 48.0% on solving $L_2$ and $L_3$ level problems, respectively. Similar results were obtained for both SVAMP and MAWPS-s, highlighting the potential of graph-based models in solving problems of varying length complexities.

For Seq2Tree models, GTS and SAU-Solver separately achieved an average improvement of 7.1% and 6.1%, respectively, compared to DNS on MAWPS-s. On Math23k, GTS achieved an average improvement of 7.4% compared to DNS, and SAU-Solver achieved an 8.3% improvement. The considerable improvements by the Seq2Tree models indicate their potential for equation representation learning using tree-structured decoders.

Surprisingly, MathEN achieved the highest problem-solving accuracy on the $L_{1}$ -level task of MAWPS-s and the $L_3$ -level task of Math23K, and also demonstrated a lower MAD value. On the other hand, DNS exhibited lower problem-solving accuracy than MathEN, and had higher MAD values, indicating that DNS is sensitive to the lengths of the expressions.

Among the four categories of solvers considered, PLM-based models demonstrated the best performance on $L_1$ , $L_2$ and $L_3$ level tasks across all datasets. Notably, Graph2Tree exhibited advantages over other lightweight models specifically in handling tasks at $L_2$ and $L_3$ levels. Furthermore, it is worth highlighting that among the lightweight models, MathEN and SAU-Solver obtained the best results for $L_1$ on MAWPS-s and Math23K, respectively. This could be due to the fact that $L_1$ level tasks typically involve very simple syntax and language structure, which can be efficiently modeled by sequence-based encoders. In contrast, $L_2$ and $L_3$ level tasks involve more complex syntax and language structures.

Another interesting finding is that, on MAWPS-s, all models performed better at solving $L_2$ level problems than the shorter $L_1$ level problems except GPT-4. Further analysis showed that the average token length of $L_1$ level problems was 26, which is significantly shorter compared to 31 and 21 on SVAMP and Math23k, respectively. It should be noted that each word is treated as a token for the English dataset MAWPS-s and SVAMP, while for the Chinese dataset Math23k, each token contains one or more words depending on the output of the applied tokenizers.

(2) Performance on solving problems indicated by expression tree height.

Table 8 shows the performances on characteristics of depth complexity. Overall, the accuracy of models decreases as the expression tree depth increases. In particular, GPT-4 achieves accuracies of 97.0% and 74.5% on the $H_1$ and $H_2$ subsets of MAWPS-s respectively. However, there is a significant performance drop of 30% from $H_1$ to $H_2$ . Similar reduction in performance is observed on Math23K. This suggests that GPT-4 is highly sensitive to the depth of the expressions.

For Graph2Tree models, an average accuracy reduction $d_{2-1}$ by 15% and 10% for all models from $H_1$ to $H_2$ level problems on MAWPS-s and Mathe23K separately. $d_{2-1}$ is an indicator of model robustness that the lower of $d_{2-1}$ is, the more robustness of the model is. This suggests that capturing the structure information hidden in problem texts is challenging work for both sequence-based and graph-based methods.

Seq2Tree models have a 7% to 10% improvement on Math23k and MAWPS-s separately compared to DNS. SAU-Solver performs better than MathEN on MAWPS-s but worse on Math23k. Graph2Tree models perform better on Math23k than Seq2Tree models. However, Graph2Tree $^1$ performs equal or better on $H_2$ level problems compared to all other methods, which indicates the latency of problem learning on complexity structures. Unlike Graph2Tree $^1$ and others, Graph2Tree $^2$ is much more insensitive for the task of depth expression prediction. This suggests that the sentence level information might enhance the representation learning of complex expressions.

For Seq2Seq models, MathEN performs better on all datasets compared to DNS, especially on Math23k $H_1$ level dataset which achieves the best result (69.2%). However, the accuracy reduction of MathEN by 15.6% and 12.9 from $H_1$ to $H_2$ level problem on MAWPS-s and Math23k separately show that MathEN is much more sensitive to expression depth than DNS.

(3) Performance on solving problems indicated by implicit condition

Table 9 demonstrates the significant advantages of PLM-based models in solving implicit condition problems. In particular, GPT-4 exhibits a 1% performance improvement on $C_2$ compared to $C_1$ . In terms of lightweight models, MathEN and Graph2Tree $^1$ obtained an outstanding performance of 67.1% and 66.4% separately. For solving implicit relation problems, MathEN achieved 61.5% which is 2.3% higher than the second-highest result obtained by GTS. Meanwhile, it shows that Seq2Tree models and Graph2Tree $^1$ method performed similarly (i.e., 59.2%, 58.6% and 58.0% separately) on solving implicit relation problems. For robustness, MathEN has the lowest $d_{2-1}$ performance among the considered models except for the Graph2Tree $^2$ .

(4) Performance on solving problems indicated by the arithmetic situation.

As depicted in Table 10 , PLM-based models achieve the best results across all four problem types. However, for Summation type problems ( $S_s$ ), MathEN achieves an impressive accuracy rate of 72.2%, which is 30% higher than that of GPT-4. Among all lightweight models, MathEN exhibits outstanding performance. For example, MathEN achieved 72.2% accuracy on solving $S_s$ type problems and GTS got 71.3% on solving Motion type problems ( $S_m$ ). Whereas the Graph2Tree models generally performed poorly on situational problems. Since situational problems contain more complex quantity relations among various math objects. These quantity relations are usually indicated by high-level contexts which are much more challenging to obtain the required quantity relations for most sequence and graph based models. Moreover, performance differs greatly on different types of situation problems even with the same model which indicates that differentiated models are required for solving different types of situational problems.

Conclusively, the experimental results revealed the following: (1) PLM-based models have shown a significant advantage over other models in almost all tasks. However, they also suffer from a rapid decline in performance when the length and depth of expressions increase. (2) Tree-based expression decoders achieved significant improvement compared to sequence-based decoders. This demonstrates the efficiency of generative models in learning the structural information hidden in mathematical expressions, compared to traditional retrieved models. (3) For encoders, graph-based models perform similarly to sequence-based models. There may be two reasons for this observation. First, current sequence and graph-based models may have encountered a technical bottleneck. These models are trained and fine-tuned for general or specific natural language tasks that are not necessarily suitable for learning mathematical relations in sophisticated situations of math word problems containing various common sense knowledge and domain knowledge. (4) Equation normalization and ensemble models (such as MathEN) achieved outstanding performance compared to pure Seq2Seq models. Since a math word problem may have more than one equation, it is necessary to normalize duplicated equations when working with current sequence and graph-based models.

Comparative analysis of math expression decoding models

To investigate the impact of the decoding models integrated with different encoding models, we conduct a confusion test of depth-first tree decoding (DT Cell) [ 6 ] and breadth-first tree decoding (BT Cell) [ 17 ] in this section. For each decoding module, encoding modules of GRU cell [ 2 ], GCN cell [ 6 ], biGraphSAGE cell [ 17 ] and BERT [ 26 ] are connected separately to compose a full pipeline of encoding-decoding network. The test is conducted on Math23k and the corresponding result is shown in Table 11 .

As shown in Table 11 , the DT cell demonstrates significant advantages in terms of accuracy for both expression and answer when combined with any encoding model. Particularly, when using GRU, GRU+GCN, and BERT as encoders, the DT cell outperforms the BT cell by more than 10%. However, when utilizing GRU+biGraphSAGE as the encoder, the DT cell shows lower performance improvements of 6.7% and 6.5% for both $E_{acc}$ and $A_{acc}$ , compared to other encoder combinations. One possible reason is that the GRU+biGraphSAGE encoder incorporates heterogeneous graph information from the problem text, which has relevance to breadth-first decomposing.

Comparative analysis of problem encoding models

Experimental results obtained in Sect. “ Performance on solving characteristic problems ” show the effectiveness of tree-structured models in math expression decoding. However, the performance of models in solving different characteristic problems varies as different neural cells are applied during encoding. In this section, a further experiment is conducted to evaluate the performance of different encoding units in solving different characteristic problems.

In the following experiments, we split the encoding modules into composable neural cells from the baseline methods for problem encoding. From sequence-based encoders, LSTM and GRU cells are obtained and GCN and biGraphSAGE cells are obtained from graph-based encoders. The obtained GRU and LSTM cells are designed with 2 layers. In our experiment, both 2 and 4-layer cells are tested to evaluate the effect of cell depth in problem encoding. The above cells are implemented individually or jointly for problem encoding followed by the tree-based decoding module [ 5 ] to generate math expressions. To combine the outputs of the GCN module and the biGraphSAGE module, a multi-head attention network is used which takes the final hidden vectors of the GCN and biGraphSAGE as input and outputs a new combined hidden vector. The $E_{acc}$ and $A_{acc}$ results are presented in Table 12 .

In Table 12 , $G_{qcell}$ and $G_{qcom}$ denote the quantity cell graph and quantity comparison graph built in [ 6 ] separately as the input of the GCN network. $G_{wcon}$ refers to the constituency graph defined in [ 17 ] and is processed by the biGraphSAGE network.

Obviously, the BERT-DT combination outperforms other combinations in almost all test items. Here, we focus on discussing the performance of lightweight model combinations.

Firstly, when selecting the number of layers for the sequence encoder, there is no significant difference in performance between 4-layer and 2-layer networks. The 2-layer GRU cell obtained the best result among all sequence-based cells. The 2-layer GRU cell performed better than the 4-layer cells and similar results were obtained by LSTM cells. Therefore, we believe that it may be not an efficient way to try to improve the problem encoding by increasing the depth of sequence-based neural networks.

Secondly, when incorporating graph information, the combination of $G_{qcom}$ and $G_{qcell}$ obtained the best performance. For GCN-based modules, the GCN cell with $G_{qcom}$ information obtained outstanding results on all levels of length complexity tasks and the $H_1$ level depth complexity task. The GCN cell performs best on $H_2$ level task when combining the graph information of $G_{qcell}$ and $G_{qcom}$ . A possible reason is that the $G_{qcell}$ is homologous to the basic text sequence while the $G_{qcom}$ contains additional comparison information that plays an important role in guiding the math expression generation. Second, the biGraphSAGE cell with $G_{wcon}$ got lower performance than GCN cells, partly due to the sparsity of the constituency matrix used.

Furthermore, considering the fusion of multiple features, it can be observed from Table 12 that the mixed module by combining GCN ( $G_{qcell}$ ) and biGraphSAGE ( $G_{wcon}$ ) achieved better performance than biGraphSAGE ( $G_{wcon}$ ) but worse than GCN ( $G_{qcell}$ ) individually applied. The performance is slightly improved after the $G_{qcom}$ is added. However, the overall performance of mixed modules is worse than only GCN modules. This leads us to conclude that choosing an appropriate encoder is a key decision in hybrid information encoding.

This paper provides a comprehensive survey and performance analysis of DL-based solvers for Math Word Problems (MWPs). These solvers are categorized into four distinct groups based on their network architecture and neural cell types: Seq2Seq-based models, Seq2Tree-based models, Graph2Tree-based models, and PLM-based models.

During the training phase, it has been observed that most models exhibit overfitting issues on datasets. Figure 5 illustrates the effectiveness of the Math23K training set, which consists of 18k instances, in meeting the training requirements of most deep learning-based models. Conversely, when trained on the MAWPS-s dataset, which contains approximately 1.5 k instances, almost all models show noticeable signs of overfitting. This particular finding serves as a valuable reference point for future endeavors involving dataset construction.

In terms of overall performance, pre-trained language models outperformed other models on both single-equation tasks and multi-equation tasks. As depicted in Table 6 , GPT-4 achieves the best results on the MAWPS-s, SVAMP, and Draw-1k datasets, and the BertTree performs well on the two Chinese datasets, Math23k and HMWP. This demonstrates the significant advantage of PLM-based models, especially large-scale language modes such as GPT-4, in solving math word problems. However, there are variations in the performance of different pre-trained language models on Chinese and English datasets. Consistent findings were also reported in previous research studies [ 26 , 27 ]. For instance, in [ 26 ], it is highlighted that the adoption of the Bert2Tree model yields a 2.1% improvement in answer accuracy compared to the Graph2Tree model on the MAWPS-s dataset, while achieving a 7% improvement on the Math23k dataset. This outcome can be attributed to two factors: (1) The Chinese pre-trained model employed in this study, namely Chinese BERT with whole word masking [ 55 ], differs from the BERT-base model used for English. Thus, it is reasonable to infer that task-specific training or fine-tuning of pre-trained language models is essential to fully leverage their advantages. (2) Pre-trained language models exhibit greater proficiency in handling MWPs with intricate semantics. As evidenced by Table 3 , the average length of question texts in the Math23k and HMWP datasets is 1.5-2 times longer than that of other datasets, suggesting the presence of more complex syntactic and semantic information. Utilizing pre-trained language models allows for improved extraction and utilization of pertinent information necessary for effective problem-solving.

Meanwhile, Tables 7 and 8 show that neural solvers are sensitive to the complexity of equations (e.g., equation length, equation tree height), as well as the length of the original problem text. However, we also found that (1) the MathEN model based on the Seq2Seq framework achieved the best results on some datasets (MAWPS-s), indicating that there is room for further optimization of the Graph2Tree framework. Further work is needed to discover the main factors influencing the performance of Graph2Tree on MAWPS-s and to improve it accordingly. (2) For all solvers on MAWPS-s, the increase in expression length did not result in a decline in solving accuracy, but rather showed varying degrees of improvement, which is completely opposite to what we observed on the other two datasets. Further research is needed to explain this phenomenon.

In terms of decoding performance, models integrated with tree decoders exhibit strong performance in generating math equations. Meanwhile, the DT Cell performed much better than the BT Cell on most datasets, making it widely used. However, we believe that the BT Cell still has its special advantages, as its decoding process is more in line with human thought in arithmetic reasoning, where a task is decomposed into multiple sub-tasks, each corresponding to a certain mathematical operation semantics. Therefore, the output results of this model can be better applied in intelligent education scenario, such as step-by-step intelligent tutoring. This raises new questions for researchers on how to design models with human-like arithmetic reasoning ability and make them run efficiently.

In terms of encoding performance, implicit information representation of problem texts plays a crucial role in enhancing the performance of models. Experimental results have shown that combining structure and non-structure information can effectively enhance solver performance. However, we found that not all structure information is equally effective, and some may be more useful in improving solving performance than others. Therefore, it is necessary to design more effective mechanisms or algorithms to determine which information should be added and how the added information can be fused with current information for maximum utility.

Moreover, the emergence of large language models such as GPT has propelled MWP-solving technology to a new stage. These models can gradually improve the accuracy of MWP solvers and their remarkable reasoning abilities enable them to generate step-by-step solutions based on prompts, which is truly impressive. However, these large language models also face challenges such as large parameter sizes and usage restrictions.

Limitations

The limitations of this study are primarily attributed to the emergence of novel models and their integration with knowledge bases, which present challenges in re-implementing these algorithms. Consequently, performance comparisons with specific papers such as [ 7 , 27 ] have been considered in this study. Additionally, due to hardware constraints, we did not fine-tune the pre-trained language models, therefore, the performance of various fine-tuned models has not been reported.

Furthermore, for PLM-based models like GPT-4 [ 30 ], advanced prompts or interaction strategies were not employed in our experiments, which may result in lower accuracy. Moreover, it is worth noting that PLM-based models have the advantage of generating descriptive solution processes, but their performance evaluation in this aspect has not been conducted in this study.

In this paper, we have aimed to provide a comprehensive and analytical comparative examination of the state-of-the-art neural solvers for math word problem solving. Our objective was to serve as a reference for researchers in the design of future models by offering insights into the structure of neural solvers, their performance, and the pros and cons of the involved neural cells.

We first identify the architectures of typical neural solvers, rigorously analyzing the framework of each category, particularly the four typical categories: Seq2Seq, Seq2Tree, Graph2Tree and PLM-based models. A four-dimensional indicator is proposed to categorize the considered datasets to precisely evaluate the performance of neural solvers in solving different characteristics of MWPs. Typical neural solvers are decomposed into highly reusable components. To evaluate the considered solvers, we have established a testbed and conducted comprehensive experiments on five popular datasets using eight representative MWP solvers, followed by a comparative analysis on the achieved results.

After conducting an in-depth analysis, we found that: (1) PLM-based models consistently demonstrate significant accuracy advantages across almost all datasets, yet there remains room for improvement to meet practical demands. (2) Models integrated with tree decoders exhibit strong performance in generating math equations. The length of expressions and the depth of expression trees are important factors affecting solver performance when solving problems with different expression features. The longer the expression and the deeper the expression tree, the lower the solver performance. (3) Implicit information representation of problem texts plays a crucial role in enhancing the performance of models. While the use of multi-modal feature representation has shown promising improvements in performance, it is crucial to ensure information complementary among modalities.

Based on our findings, we have the following suggestions for future work. Firstly, there is still room to improve the performance of solvers, including problem representation learning, multi-solution generation, etc.

Secondly, to better support the potential real-world applications in education, the output of solvers should be more comprehensive. Solvers are expected to generate decomposable and interpretable solutions, rather than just simple expressions or answers. The emergence of large language models has provided ideas for addressing this issue, but it remains a challenge to ensure the validity and interpretability of the outputs for teaching and tutoring applications.

Finally, to evaluate the neural solvers more comprehensively, it is necessary to develop more diverse metrics and evaluation methods in future research. These metrics and methods should capture the performance of solvers in problem understanding, automatic addition of implicit knowledge, solution reasoning, interpretability of results, and other relevant aspects.

Data Availability

The data used in this study is available from the corresponding author upon reasonable request.

Abbreviations

Math Word Problems

Pre-trained Language Model

Tree-structural Decoder

Deep Learning

Depth-first decomposing Tree

Breadth-first decomposing Tree

Mean accuracy difference

Universal Expression Tree

Unit Dependency Graph

Explanation

Problem text

Word token of the P

Encoding network

Decoding network

The hidden vector state i

the query matrix, key matrix and value matrix separately

A graph with vertex V and edge E

trainable parameters and bias

Expression length

Expression tree depth

Implicit condition

Arithmetic situation

Equation accuracy

Math expressions

Answer accuracy

Zhang D, Wang L, Zhang L, Dai BT, Shen HT (2019) The gap of semantic parsing: a survey on automatic math word problem solvers. IEEE Trans Pattern Anal Mach Intell 42(9):2287–2305

Article Google Scholar

Wang Y, Liu X, Shi S (2017) Deep neural solver for math word problems. In: Proceedings of the 2017 Conference on Empirical Methods in Natural Language Processing, pp. 845–854. Association for Computational Linguistics, Copenhagen, Denmark

Greff K, Srivastava RK, Koutník J, Steunebrink BR, Schmidhuber J (2017) LSTM: a search space odyssey. IEEE Trans Neural Netw Learn Syst 28(10):2222–2232

Article MathSciNet Google Scholar

Wang L, Wang Y, Cai D, Zhang D, Liu X (2018) Translating a math word problem to a expression tree. In: Proceedings of the 2018 Conference on Empirical Methods in Natural Language Processing, pp. 1064–1069. Association for Computational Linguistics, Brussels, Belgium

Xie Z, Sun S (2019) A goal-driven tree-structured neural model for math word problems. In: Proceedings of the Twenty-Eighth International Joint Conference on Artificial Intelligence, pp. 5299–5305. International Joint Conferences on Artificial Intelligence Organization, Macao, China

Zhang J, Wang L, Lee RKW, Bin Y, Wang Y, Shao J, Lim EP (2020) Graph-to-tree learning for solving math word problems. In: Proceedings of the 58th Annual Meeting of the Association for Computational Linguistics, pp. 3928–3937. Association for Computational Linguistics, Seattle, USA

Wu Q, Zhang Q, Wei Z (2021) An edge-enhanced hierarchical graph-to-tree network for math word problem solving. In: Findings of the Association for Computational Linguistics: EMNLP 2021, pp. 1473–1482. Association for Computational Linguistics, Punta Cana, Dominican Republic

Yang Z, Qin J, Chen J, Lin L, Liang X (2022) LogicSolver: Towards interpretable math word problem solving with logical prompt-enhanced learning. In: Findings of the Association for Computational Linguistics: EMNLP 2022, pp. 1–13. Association for Computational Linguistics, Abu Dhabi, United Arab Emirates

Jie Z, Li J, Lu W (2022) Learning to reason deductively: Math word problem solving as complex relation extraction. In: Proceedings of the 60th Annual Meeting of the Association for Computational Linguistics, pp. 5944–5955. Association for Computational Linguistics, Dublin, Ireland

Lan Y, Wang L, Zhang Q, Lan Y, Dai BT, Wang Y, Zhang D, Lim EP (2022) Mwptoolkit: An open-source framework for deep learning-based math word problem solvers. Proceedings of the AAAI Conference on Artificial Intelligence 36:13188–13190

Vaswani A, Shazeer N, Parmar N, Uszkoreit J, Jones L, Gomez AN, Kaiser L, Polosukhin I (2017) Attention is all you need. In: Proceedings of the 31st International Conference on Neural Information Processing Systems, NIPS’17, pp. 6000–6010. Curran Associates Inc., Red Hook, NY, USA

Lin JCW, Shao Y, Djenouri Y, Yun U (2021) ASRNN: a recurrent neural network with an attention model for sequence labeling. Knowl-Based Syst 212:106548

Chiang TR, Chen YN (2019) Semantically-aligned equation generation for solving and reasoning math word problems. In: Proceedings of the 2019 Conference of the North American Chapter of the Association for Computational Linguistics: Human Language Technologie, pp. 2656–2668. Association for Computational Linguistics, Minneapolis, Minnesota

Hong Y, Li Q, Ciao D, Haung S, Zhu SC (2021) Learning by fixing: Solving math word problems with weak supervision. In: Proceedings of the AAAI Conference on Artificial Intelligence, 35:4959–4967

Hong Y, Li Q, Gong R, Ciao D, Huang S, Zhu SC (2021) SMART: a situation model for algebra story problems via attributed grammar. In: Proceedings of the 2021 AAAI Conference on Artificial Intelligence, pp. 13009–13017. Vancouver, Canada

Roy S, Roth D (2017) Unit dependency graph and its application to arithmetic word problem solving. In: Proceedings of the Thirty-First AAAI Conference on Artificial Intelligence, pp. 3082–3088. San Francisco, USA

Li S, Wu L, Feng S, Xu F, Xu F, Zhong S (2020) Graph-to-tree neural networks for learning structured input-output translation with applications to semantic parsing and math word problem. In: Findings of the Association for Computational Linguistics: EMNLP 2020, pp. 2841–2852. Association for Computational Linguistics, Punta Cana, Dominican Republic

Hochreiter S, Schmidhuber J (1997) Long short-term memory. Neural Comput 9(8):1735–1780

Bahdanau D, Cho KH, Bengio Y (2015) Neural machine translation by jointly learning to align and translate. In: 3rd International Conference on Learning Representations. San Diego, California

Cai D, Lam W (2020) Graph transformer for graph-to-sequence learning. Proceedings of the AAAI Conference on Artificial Intelligence 34:7464–7471

Hamilton WL, Ying R, Leskovec J (2017) Inductive representation learning on large graphs. In: Proceedings of the 31st International Conference on Neural Information Processing Systems, pp. 1025–1035. Curran Associates Inc., Red Hook, NY, USA

Mukherjee A, Garain U (2008) A review of methods for automatic understanding of natural language mathematical problems. Artificial Intell Rev 29(2):93–122

Meadows J, Freitas A (2022) A survey in mathematical language processing. arXiv:2205.15231 [cs]

Lu P, Qiu L, Yu W, Welleck S, Chang KW (2023) A survey of deep learning for mathematical reasoning. arXiv:2212.10535 [cs]

Liu Q, Guan W, Li S, Kawahara D (2019) Tree-structured decoding for solving math word problems. In: Proceedings of the 2019 Conference on Empirical Methods in Natural Language Processing and the 9th International Joint Conference on Natural Language Processing (EMNLP-IJCNLP), pp. 2370–2379. Association for Computational Linguistics, Hong Kong, China

Liang Z, Zhang J, Wang L, Qin W, Lan Y, Shao J, Zhang X (2022) MWP-BERT: Numeracy-augmented pre-training for math word problem solving. In: Findings of the Association for Computational Linguistics: NAACL 2022, pp. 997–1009. Association for Computational Linguistics, Seattle, United States

Zhang W, Shen Y, Ma Y, Cheng X, Tan Z, Nong Q, Lu W (2022) Multi-view reasoning: Consistent contrastive learning for math word problem. In: Findings of the Association for Computational Linguistics: EMNLP 2022, pp. 1103–1116. Association for Computational Linguistics, Abu Dhabi, United Arab Emirates

Brown T, Mann B, Ryder N, Subbiah M, Kaplan JD, Dhariwal P, Neelakantan A, Shyam P, Sastry G, Askell A, Agarwal S, Herbert-Voss A, Krueger G, Henighan T, Child R, Ramesh A, Ziegler D, Wu J, Winter C, Hesse C, Chen M, Sigler E, Litwin M, Gray S, Chess B, Clark J, Berner C, McCandlish S, Radford A, Sutskever I, Amodei D (2020) Language models are few-shot learners. In: Advances in Neural Information Processing Systems, 33:1877–1901. Curran Associates, Inc

Radford A, Wu J, Child R, Luan D, Amodei D, Sutskever I (2019) Language models are unsupervised multitask learners. Tech. rep., OpenAI. OpenAI blog

Zhou A, Wang K, Lu Z, Shi W, Luo S, Qin Z, Lu S, Jia A, Song L, Zhan M, Li H (2023) Solving challenging math word problems using GPT-4 code interpreter with code-based self-verification. https://doi.org/10.48550/arXiv.2308.07921 . arXiv:2308.07921 [cs]

Fletcher CR (1985) Understanding and solving arithmetic word problems: a computer simulation. Behav Res Methods Instruments Comput 17(5):565–571

Kushman N, Artzi Y, Zettlemoyer L, Barzilay R (2014) Learning to automatically solve algebra word problems. In: Proceedings of the 52nd Annual Meeting of the Association for Computational Linguistics, pp. 271–281. Association for Computational Linguistics, Baltimore, Maryland

Shen Y, Jin C (2020) Solving math word problems with multi-encoders and multi-decoders. In: Proceedings of the 28th International Conference on Computational Linguistics, pp. 2924–2934. International Committee on Computational Linguistics, Barcelona, Spain

Liang CC, Hsu KY, Huang CT, Li CM, Miao SY, Su KY (2016) A tag-based statistical english math word problem solver with understanding, reasoning and explanation. In: Proceedings of the Twenty-Fifth International Joint Conference on Artificial Intelligence, pp. 4254–4255. San Diego, USA

Devlin J, Chang MW, Lee K, Toutanova K (2019) BERT: Pre-training of deep bidirectional transformers for language understanding. In: Proceedings of the 2019 Conference of the North American Chapter of the Association for Computational Linguistics: Human Language Technologies, Volume 1 (Long and Short Papers), pp. 4171–4186. Association for Computational Linguistics, Minneapolis, Minnesota

Wang L, Zhang D, Zhang J, Xu X, Gao L, Dai BT, Shen HT (2019) Template-based math word problem solvers with recursive neural networks. In: Proceedings of the Thirty-Third AAAI Conference on Artificial Intelligence and Thirty-First Innovative Applications of Artificial Intelligence Conference and Ninth AAAI Symposium on Educational Advances in Artificial Intelligence, pp. 7144–7151. AAAI Press, Hawaii, USA

Li J, Wang L, Zhang J, Wang Y, Dai BT, Zhang D (2019) Modeling intra-relation in math word problems with different functional multi-head attentions. In: Proceedings of the 57th Annual Meeting of the Association for Computational Linguistics, pp. 6162–6167. Association for Computational Linguistics

Qin J, Lin L, Liang X, Zhang R, Lin L (2020) Semantically-aligned universal tree-structured solver for math word problems. In: Proceedings of the 2020 Conference on Empirical Methods in Natural Language Processing (EMNLP), pp. 3780–3789. Association for Computational Linguistics, Punta Cana, Dominican Republic

Wu Q, Zhang Q, Wei Z, Huang X (2021) Math word problem solving with explicit numerical values. In: Proceedings of the 59th Annual Meeting of the Association for Computational Linguistics and the 11th International Joint Conference on Natural Language Processing, pp. 5859–5869. Association for Computational Linguistics, Bangkok, Thailand

Yu W, Wen Y, Zheng F, Xiao N (2021) Improving math word problems with pre-trained knowledge and hierarchical reasoning. In: Proceedings of the 2021 Conference on Empirical Methods in Natural Language Processing, pp. 3384–3394. Association for Computational Linguistics, Online and Punta Cana, Dominican Republic

Li Z, Zhang W, Yan C, Zhou Q, Li C, Liu H, Cao Y (2022) Seeking patterns, not just memorizing procedures: Contrastive learning for solving math word problems. In: Findings of the Association for Computational Linguistics: ACL 2022, pp. 2486–2496. Association for Computational Linguistics, Dublin, Ireland

Shen J, Yin Y, Li L, Shang L, Jiang X, Zhang M, Liu Q (2021) Generate & rank: A multi-task framework for math word problems. In: Findings of the Association for Computational Linguistics: EMNLP 2021, pp. 2269–2279. Association for Computational Linguistics, Punta Cana, Dominican Republic

Shen Y, Liu Q, Mao Z, Cheng F, Kurohashi S (2022) Textual enhanced contrastive learning for solving math word problems. In: Findings of the Association for Computational Linguistics: EMNLP 2022, pp. 4297–4307. Association for Computational Linguistics, Abu Dhabi, United Arab Emirates

Chowdhery A, Narang S, Devlin J, Bosma M, Mishra G, Roberts A, Barham P, Chung HW, Sutton C, Gehrmann S, Schuh P, Shi K, Tsvyashchenko S, Maynez J, Rao A, Barnes P, Tay Y, Shazeer N, Prabhakaran V, Reif E, Du N, Hutchinson B, Pope R, Bradbury J, Austin J, Isard M, Gur-Ari G, Yin P, Duke T, Levskaya A, Ghemawat S, Dev S, Michalewski H, Garcia X, Misra V, Robinson K, Fedus L, Zhou D, Ippolito D, Luan D, Lim H, Zoph B, Spiridonov A, Sepassi R, Dohan D, Agrawal S, Omernick M, Dai AM, Pillai TS, Pellat M, Lewkowycz A, Moreira E, Child R, Polozov O, Lee K, Zhou Z, Wang X, Saeta B, Diaz M, Firat O, Catasta M, Wei J, Meier-Hellstern K, Eck D, Dean J, Petrov S, Fiedel N (2022) PaLM: Scaling language modeling with pathways . arXiv:2204.02311 [cs]

Lewkowycz A, Andreassen A, Dohan D, Dyer E, Michalewski H, Ramasesh V, Slone A, Anil C, Schlag I, Gutman-Solo T, Wu Y, Neyshabur B, Gur-Ari G, Misra V (2022) Solving Quantitative Reasoning Problems with Language Models. In: Advances in Neural Information Processing Systems, vol. 35, pp. 3843–3857. Curran Associates, Inc

Touvron H, Lavril T, Izacard G, Martinet X, Lachaux MA, Lacroix T, Rozière B, Goyal N, Hambro E, Azhar F, Rodriguez A, Joulin A, Grave E, Lample G (2023). LLaMA: Open and efficient foundation language models https://doi.org/10.48550/arXiv.2302.13971 . arXiv:2302.13971 [cs]

Chung J, Gulcehre C, Cho K, Bengio Y (2014) Empirical evaluation of gated recurrent neural networks on sequence modeling. In: NIPS 2014 Workshop on Deep Learning, December 2014. Montreal, Canada

Ghazvini A, Abdullah SNHS, Kamru Hasan M, Bin Kasim DZA (2020) Crime spatiotemporal prediction with fused objective function in time delay neural network. IEEE Access 8:115167–115183

Djenouri Y, Srivastava G, Lin JCW (2021) Fast and accurate convolution neural network for detecting manufacturing data. IEEE Trans Ind Inform 17(4):2947–2955

Wu Q, Zhang Q, Fu J, Huang X (2020) A knowledge-aware sequence-to-tree network for math word problem solving. In: Proceedings of the 2020 Conference on Empirical Methods in Natural Language Processing (EMNLP), pp. 7137–7146. Association for Computational Linguistics, Punta Cana, Dominican Republic

Gupta A, Kumar S, Kumar P S (2023) Solving age-word problems using domain ontology and bert. In: Proceedings of the 6th Joint International Conference on Data Science & Management of Data, pp. 95–103. ACM, New York, NY, USA

Petroni F, Rocktäschel T, Riedel S, Lewis P, Bakhtin A, Wu Y, Miller A (2019) Language models as knowledge bases? In: Proceedings of the 2019 Conference on Empirical Methods in Natural Language Processing and the 9th International Joint Conference on Natural Language Processing (EMNLP-IJCNLP), pp. 2463–2473. Association for Computational Linguistics, Hong Kong, China

Jiang Z, Xu FF, Araki J, Neubig G (2020) How can we know what language models know? Trans Assoc Comput Linguistics 8:423–438 ( Place: Cambridge, MA Publisher: MIT Press )

Liu Z, Lin W, Shi Y, Zhao J (2021) A robustly optimized bert pre-training approach with post-training. In: Proceedings of the 20th Chinese National Conference on Computational Linguistics, pp. 1218–1227. Chinese Information Processing Society of China, Huhhot, China

Cui Y, Che W, Liu T, Qin B, Yang Z, Wang S, Hu G (2019) Pre-training with whole word masking for chinese bert. IEEE/ACM Trans Audio Speech Language Process 29:3504–3514

Chen J, Pan X, Yu D, Song K, Wang X, Yu D, Chen J (2023) Skills-in-context prompting: Unlocking compositionality in large language models. https://doi.org/10.48550/arXiv.2308.00304 . arXiv:2308.00304 [cs]

Wei J, Wang X, Schuurmans D, Bosma M, ichter b, Xia F, Chi E, Le QV, Zhou D (2022) Chain-of-thought prompting elicits reasoning in large language models. In: Advances in Neural Information Processing Systems, vol. 35, pp. 24824–24837. Curran Associates, Inc

Huang X, Ruan W, Huang W, Jin G, Dong Y, Wu C, Bensalem S, Mu R, Qi Y, Zhao X, Cai K, Zhang Y, Wu S, Xu P, Wu D, Freitas A, Mustafa MA (2023) A survey of safety and trustworthiness of large language models through the lens of verification and validation. http://arxiv.org/abs/2305.11391 . arXiv:2305.11391 [cs]

Dong L, Lapata M (2016) Language to logical form with neural attention. In: Proceedings of the 54th Annual Meeting of the Association for Computational Linguistics (Volume 1: Long Papers), pp. 33–43. Association for Computational Linguistics, Berlin, Germany

Zhang J, Lee RKW, Lim EP, Qin W, Wang L, Shao J, Sun Q (2020) Teacher-student networks with multiple decoders for solving math word problem. In: Proceedings of the Twenty-Ninth International Joint Conference on Artificial Intelligence, pp. 4011–4017. International Joint Conferences on Artificial Intelligence Organization, Yokohama, Japan

Bobrow DG (1964) Natural language input for a computer problem solving system. Tech. rep., Massachusetts Institute of Technology, USA

Bakman Y (2007) Robust understanding of word problems with extraneous information. arXiv General Mathematics. https://api.semanticscholar.org/CorpusID:117981901

Koncel-Kedziorski R, Hajishirzi H, Sabharwal A, Etzioni O, Ang SD (2015) Parsing algebraic word problems into equations. Trans Assoc Comput Linguistics 3:585–597 ( Place: Cambridge, MA )

Roy S, Upadhyay S, Roth D (2016) Equation parsing: Mapping sentences to grounded equations. In: Proceedings of the 2016 Conference on Empirical Methods in Natural Language Processing, pp. 1088–1097. Association for Computational Linguistics, Austin, Texas

Wang L, Zhang D, Gao L, Song J, Guo L, Shen HT (2018) MathDQN: Solving arithmetic word problems via deep reinforcement learning. In: Proceedings of the Thirty-Second AAAI Conference on Artificial Intelligence, pp. 5545–5552. AAAI Press, New Orleans, USA

Hosseini MJ, Hajishirzi H, Etzioni O, Kushman N (2014) Learning to solve arithmetic word problems with verb categorization. In: Proceedings of the 2014 Conference on Empirical Methods in Natural Language Processing (EMNLP), pp. 523–533. Association for Computational Linguistics, Doha, Qatar

Shi S, Wang Y, Lin CY, Liu X, Rui Y (2015) Automatically solving number word problems by semantic parsing and reasoning. In: Proceedings of the 2015 Conference on Empirical Methods in Natural Language Processing, pp. 1132–1142. Lisbon, Portugal

Liang CC, Hsu KY, Huang CT, Li CM, Miao SY, Su KY (2016) A tag-based English math word problem solver with understanding, reasoning and explanation. In: Proceedings of the 2016 Conference of the North American Chapter of the Association for Computational Linguistics: Demonstrations, pp. 67–71. Association for Computational Linguistics, San Diego, California

Upadhyay S, Chang MW, Chang KW, Yih Wt (2016) Learning from explicit and implicit supervision jointly for algebra word problems. In: Proceedings of the 2016 Conference on Empirical Methods in Natural Language Processing, pp. 297–306. Association for Computational Linguistics, Austin, Texas

Chen S, Zhou M, He B, Wang P, Wang Z (2022) A comparative analysis of math word problem solving on characterized datasets. In: In Proceedings of the 2022 International Conference on Intelligent Education and Intelligent Research. IEEE, Wuhan, China

He B, Chen S, Miao Z, Liang G, Pan K, Huang L (2022) Comparative analysis of problem representation learning in math word problem solving. In: In Proceedings of the 2022 International Conference on Intelligent Education and Intelligent Research. IEEE, Wuhan, China

Roy S, Roth D (2015) Solving general arithmetic word problems. In: Proceedings of the 2015 Conference on Empirical Methods in Natural Language Processing, pp. 1743–1752. Association for Computational Linguistics, Lisbon, Portugal

Yenduri G, M R, G CS, Y S, Srivastava G, Maddikunta PKR, G DR, Jhaveri RH, B P, Wang W, Vasilakos AV, Gadekallu TR (2023) Generative pre-trained transformer: A comprehensive review on enabling technologies, potential applications, emerging challenges, and future directions. arXiv:2305.10435

Zhang H, Lu G, Zhan M, Zhang B (2021) Semi-supervised classification of graph convolutional networks with laplacian rank constraints. Neural Process Lett 54(4):2645–2656

Zhou L, Dai S, Chen L (2015) Learn to solve algebra word problems using quadratic programming. In: Proceedings of the 2015 Conference on Empirical Methods in Natural Language Processing, pp. 817–822. Association for Computational Linguistics, Lisbon, Portugal

Koncel-Kedziorski R, Roy S, Amini A, Kushman N, Hajishirzi H (2016) MAWPS: A math word problem repository. In: Proceedings of the 2016 Conference of the North American Chapter of the Association for Computational Linguistics: Human Language Technologies, pp. 1152–1157. Association for Computational Linguistics, San Diego, California

Huang D, Shi S, Lin CY, Yin J, Ma WY (2016) How well do computers solve math word problems? Large-scale dataset construction and evaluation. In: Proceedings of the 54th Annual Meeting of the Association for Computational Linguistics, pp. 887–896. Association for Computational Linguistics, Berlin, Germany

Upadhyay S, Chang MW (2017) Annotating derivations: A new evaluation strategy and dataset for algebra word problems. In: Proceedings of the 15th Conference of the European Chapter of the Association for Computational Linguistics, pp. 494–504. Association for Computational Linguistics, Valencia, Spain

Patel A, Bhattamishra S, Goyal N (2021) Are NLP models really able to solve simple math word problems? In: Proceedings of the 2021 Conference of the North American Chapter of the Association for Computational Linguistics: Human Language Technologies, pp. 2080–2094. Association for Computational Linguistics, Bangkok, Thailand

Download references

Acknowledgements

This work is supported by the National Natural Science Foundation of China (No. 62007014) and the Humanities and Social Sciences Youth Fund of the Ministry of Education (No. 20YJC880024).

Author information

Authors and affiliations.

Faculty of Artificial Intelligence in Education, Central China Normal University, Wuhan, China

Bin He, Xinguo Yu, Litian Huang, Hao Meng, Guanghua Liang & Shengnan Chen

You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Xinguo Yu .

Ethics declarations

Conflict of interest.

The authors declare that they have no Conflict of interest.

Additional information

Publisher's note.

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/ .

Reprints and permissions

About this article

He, B., Yu, X., Huang, L. et al. Comparative study of typical neural solvers in solving math word problems. Complex Intell. Syst. (2024). https://doi.org/10.1007/s40747-024-01454-8

Download citation

Received : 27 March 2023

Accepted : 17 April 2024

Published : 22 May 2024

DOI : https://doi.org/10.1007/s40747-024-01454-8

Share this article

Anyone you share the following link with will be able to read this content:

Sorry, a shareable link is not currently available for this article.

Provided by the Springer Nature SharedIt content-sharing initiative

Comparative analysis
Deep learning model
Math word problem solving
Find a journal
Publish with us
Track your research

SUGGESTED TOPICS
The Magazine
Newsletters
Managing Yourself
Managing Teams
Work-life Balance
The Big Idea
Data & Visuals
Reading Lists
Case Selections
HBR Learning
Topic Feeds
Account Settings
Email Preferences

4 Common Types of Team Conflict — and How to Resolve Them

Randall S. Peterson,
Priti Pradhan Shah,
Amanda J. Ferguson,
Stephen L. Jones

Advice backed by three decades of research into thousands of team conflicts around the world.

Managers spend 20% of their time on average managing team conflict. Over the past three decades, the authors have studied thousands of team conflicts around the world and have identified four common patterns of team conflict. The first occurs when conflict revolves around a single member of a team (20-25% of team conflicts). The second is when two members of a team disagree (the most common team conflict at 35%). The third is when two subgroups in a team are at odds (20-25%). The fourth is when all members of a team are disagreeing in a whole-team conflict (less than 15%). The authors suggest strategies to tailor a conflict resolution approach for each type, so that managers can address conflict as close to its origin as possible.

If you have ever managed a team or worked on one, you know that conflict within a team is as inevitable as it is distracting. Many managers avoid dealing with conflict in their team where possible, hoping reasonable people can work it out. Despite this, research shows that managers spend upwards of 20% of their time on average managing conflict.

Randall S. Peterson is the academic director of the Leadership Institute and a professor of organizational behavior at London Business School. He teaches leadership on the School’s Senior Executive and Accelerated Development Program.
PS Priti Pradhan Shah is a professor in the Department of Work and Organization at the Carlson School of Management at the University of Minnesota. She teaches negotiation in the School’s Executive Education and MBA Programs.
AF Amanda J. Ferguson is an associate professor of Management at Northern Illinois University. She teaches Organizational Behavior and Leading Teams in the School’s MBA programs.
SJ Stephen L. Jones is an associate professor of Management at the University of Washington Bothell. He teaches Organizational and Strategic Management at the MBA level.

Partner Center

Facility for Rare Isotope Beams

At michigan state university, international research team uses wavefunction matching to solve quantum many-body problems, new approach makes calculations with realistic interactions possible.

FRIB researchers are part of an international research team solving challenging computational problems in quantum physics using a new method called wavefunction matching. The new approach has applications to fields such as nuclear physics, where it is enabling theoretical calculations of atomic nuclei that were previously not possible. The details are published in Nature (“Wavefunction matching for solving quantum many-body problems”) .

Ab initio methods and their computational challenges

An ab initio method describes a complex system by starting from a description of its elementary components and their interactions. For the case of nuclear physics, the elementary components are protons and neutrons. Some key questions that ab initio calculations can help address are the binding energies and properties of atomic nuclei not yet observed and linking nuclear structure to the underlying interactions among protons and neutrons.

Yet, some ab initio methods struggle to produce reliable calculations for systems with complex interactions. One such method is quantum Monte Carlo simulations. In quantum Monte Carlo simulations, quantities are computed using random or stochastic processes. While quantum Monte Carlo simulations can be efficient and powerful, they have a significant weakness: the sign problem. The sign problem develops when positive and negative weight contributions cancel each other out. This cancellation results in inaccurate final predictions. It is often the case that quantum Monte Carlo simulations can be performed for an approximate or simplified interaction, but the corresponding simulations for realistic interactions produce severe sign problems and are therefore not possible.

Using ‘plastic surgery’ to make calculations possible

The new wavefunction-matching approach is designed to solve such computational problems. The research team—from Gaziantep Islam Science and Technology University in Turkey; University of Bonn, Ruhr University Bochum, and Forschungszentrum Jülich in Germany; Institute for Basic Science in South Korea; South China Normal University, Sun Yat-Sen University, and Graduate School of China Academy of Engineering Physics in China; Tbilisi State University in Georgia; CEA Paris-Saclay and Université Paris-Saclay in France; and Mississippi State University and the Facility for Rare Isotope Beams (FRIB) at Michigan State University (MSU)—includes Dean Lee , professor of physics at FRIB and in MSU’s Department of Physics and Astronomy and head of the Theoretical Nuclear Science department at FRIB, and Yuan-Zhuo Ma , postdoctoral research associate at FRIB.

“We are often faced with the situation that we can perform calculations using a simple approximate interaction, but realistic high-fidelity interactions cause severe computational problems,” said Lee. “Wavefunction matching solves this problem by doing plastic surgery. It removes the short-distance part of the high-fidelity interaction, and replaces it with the short-distance part of an easily computable interaction.”

This transformation is done in a way that preserves all of the important properties of the original realistic interaction. Since the new wavefunctions look similar to that of the easily computable interaction, researchers can now perform calculations using the easily computable interaction and apply a standard procedure for handling small corrections called perturbation theory. A team effort

The research team applied this new method to lattice quantum Monte Carlo simulations for light nuclei, medium-mass nuclei, neutron matter, and nuclear matter. Using precise ab initio calculations, the results closely matched real-world data on nuclear properties such as size, structure, and binding energies. Calculations that were once impossible due to the sign problem can now be performed using wavefunction matching.

“It is a fantastic project and an excellent opportunity to work with the brightest nuclear scientist s in FRIB and around the globe,” said Ma. “As a theorist , I'm also very excited about programming and conducting research on the world's most powerful exascale supercomputers, such as Frontier , which allows us to implement wavefunction matching to explore the mysteries of nuclear physics.”

While the research team focused solely on quantum Monte Carlo simulations, wavefunction matching should be useful for many different ab initio approaches, including both classical and quantum computing calculations. The researchers at FRIB worked with collaborators at institutions in China, France, Germany, South Korea, Turkey, and United States.

“The work is the culmination of effort over many years to handle the computational problems associated with realistic high-fidelity nuclear interactions,” said Lee. “It is very satisfying to see that the computational problems are cleanly resolved with this new approach. We are grateful to all of the collaboration members who contributed to this project, in particular, the lead author, Serdar Elhatisari.”

This material is based upon work supported by the U.S. Department of Energy, the U.S. National Science Foundation, the German Research Foundation, the National Natural Science Foundation of China, the Chinese Academy of Sciences President’s International Fellowship Initiative, Volkswagen Stiftung, the European Research Council, the Scientific and Technological Research Council of Turkey, the National Natural Science Foundation of China, the National Security Academic Fund, the Rare Isotope Science Project of the Institute for Basic Science, the National Research Foundation of Korea, the Institute for Basic Science, and the Espace de Structure et de réactions Nucléaires Théorique.

Michigan State University operates the Facility for Rare Isotope Beams (FRIB) as a user facility for the U.S. Department of Energy Office of Science (DOE-SC), supporting the mission of the DOE-SC Office of Nuclear Physics. Hosting what is designed to be the most powerful heavy-ion accelerator, FRIB enables scientists to make discoveries about the properties of rare isotopes in order to better understand the physics of nuclei, nuclear astrophysics, fundamental interactions, and applications for society, including in medicine, homeland security, and industry.

The U.S. Department of Energy Office of Science is the single largest supporter of basic research in the physical sciences in the United States and is working to address some of today’s most pressing challenges. For more information, visit energy.gov/science.

IMAGES

Problem-Solving Strategies: Definition and 5 Techniques to Try
5 step problem solving method
problem solving guide step
5 step problem solving method
Comparison of Various Problem Solving Methods Explained with Example
5 Problem Solving Strategies to Become a Better Problem Solver

VIDEO

Assignment Problem ( Brute force method) Design and Analysis of Algorithm
September 16, 2021 Assignment problem| Part 2
Assignment problem
ASSIGNMENT PROBLEM: meaning, formulation, Hungarian method
Balanced assignment problem in Operations Research
Solving Assignment Problem with Scipy, NetworkX, and OR-Tools Python API's

COMMENTS

Assignment Problem: Meaning, Methods and Variations
After reading this article you will learn about:- 1. Meaning of Assignment Problem 2. Definition of Assignment Problem 3. Mathematical Formulation 4. Hungarian Method 5. Variations. Meaning of Assignment Problem: An assignment problem is a particular case of transportation problem where the objective is to assign a number of resources to an equal number of activities so as to minimise total ...
Assignment problem
Worked example of assigning tasks to an unequal number of workers using the Hungarian method. The assignment problem is a fundamental combinatorial optimization problem. In its most general form, the problem is as follows: The problem instance has a number of agents and a number of tasks.Any agent can be assigned to perform any task, incurring some cost that may vary depending on the agent ...
How to Solve the Assignment Problem: A Complete Guide
Here, we will focus on the steps involved in solving the assignment problem using the Hungarian method, which is the most commonly used and efficient method. Step 1: Set up the cost matrix. The first step in solving the assignment problem is to set up the cost matrix, which represents the cost of assigning a task to an agent.
PDF Chapter8 ASSIGNMENT PROBLEM
Connection Between Transportation and Assignment Problem An assignment problem is a special case of transportation problem in which m = n, all a i and b j are unity and each is limited to either 0 or 1. Hungarian Method for Solving an Assignment Problem 1. Prepare a square n n matrix. If not, make it square by adding suitable number of dummy ...
Assignment problem
The assignment problem arises when $ m = n $ and all $ a _ {i} $ and $ b _ {j} $ are $ 1 $. If all $ a _ {i} $ and $ b _ {j} $ in the transposed problem are integers, then there is an optimal solution for which all $ x _ {ij } $ are integers (Dantzig's theorem on integral solutions of the transport problem).
Assignment Problem: Meaning, Methods and Variations
After reading this article you will learn about:- 1. Means of Association Problem 2. Definition of Assignment Problem 3. Mathematical Formulation 4. Hungarian Method 5. Variations. Meaning of Assignment Problem: An assignment problem is an particular case of transportation problem where the objective is to assign a number of funds to an equal number of active so because at minimise full cost ...
Chapter 5: Assignment Problem
The assignment problem is one of the special type of transportation problem for which more efficient (less-time consuming) solution method has been devised by KUHN (1956) and FLOOD (1956). The justification of the steps leading to the solution is based on theorems proved by Hungarian mathematicians KONEIG (1950) and EGERVARY (1953), hence the ...
The assignment problem revisited
First, we give a detailed review of two algorithms that solve the minimization case of the assignment problem, the Bertsekas auction algorithm and the Goldberg & Kennedy algorithm. It was previously alluded that both algorithms are equivalent. We give a detailed proof that these algorithms are equivalent. Also, we perform experimental results comparing the performance of three algorithms for ...
Solving an Assignment Problem
Solving an Assignment Problem Stay organized with collections Save and categorize content based on your preferences. This section presents an example that shows how to solve an assignment problem using both the MIP solver and the CP-SAT solver. Example. In the example there are five workers (numbered 0-4) and four tasks (numbered 0-3). ...
Successful Strategies for Solving Problems on Assignments
Analysis Stage. Read the problem carefully at least twice, aloud if possible, then restate the problem in your own words. Write down all the information that you know in the problem and separate, if necessary, the "givens" from the "constraints.". Think about what can be done with the information that is given.
Solution of assignment problems (Hungarian Method)
Step :4 If each row and each column contains exactly one assignment, then the solution is optimal. Example 10.7. Solve the following assignment problem. Cell values represent cost of assigning job A, B, C and D to the machines I, II, III and IV. Solution: Here the number of rows and columns are equal. ∴ The given assignment problem is ...
ES-3: Lesson 9. SOLUTION OF ASSIGNMENT PROBLEM
The assignment problem can be solved by the following four methods: a) Complete enumeration method. b) Simplex Method. c) Transportation method. d) Hungarian method. 9.2.1 Complete enumeration method. In this method, a list of all possible assignments among the given resources and activities is prepared.
PDF THIRTEEN PROBLEM-SOLVING MODELS
The Six-Step method provides a focused procedure for the problem solving (PS) group. It ensures consistency, as everyone understands the approach to be used. By using data, it helps eliminate bias and preconceptions, leading to greater objectivity. It helps to remove divisions and encourages collaborative working.
PDF New Proposed Method for Solving Assignment Problem and Comparative
III. New Approach For Solving Assignment Problem In this section we introduce a new approach for solving Assignment problem with the help of HA-method and MOA-method but different from them. This new method is easy procedure to solve Assignment problem. Also an example is solved by this method and the result is compared to HA-method and MOA-method.
An Efficient Alternative Approach to Solve an Assignment Problem
problem with linear programming is the assignment problem. A new method has been developed in this paper to solve an assignment problem, which shows that this method provides an optimum result as well. The proposed approach has been illustrated with some numerical examples to demonstrate its effectiveness. The programming
An Alternative Approach for Solving Unbalanced Assignment Problems
modified to solve the assignment problem [3],[4],[5]. Also the signature method for the assignment problem was presented by Balinski [6]. Kore [7] proposed a new approach to solve an unbalanced assignment problem without balancing it. Basirzadeh [8] developed a Hungarian-like method,
Assignment Problem, Linear Programming
The assignment problem is a special type of transportation problem, where the objective is to minimize the cost or time of completing a number of jobs by a number of persons. In other words, when the problem involves the allocation of n different facilities to n different tasks, it is often termed as an assignment problem.
Generalized Assignment Problem
The generalized assignment problem (GAP) seeks the minimum cost assignment of n tasks to m agents such that each task is assigned to precisely one agent subject to capacity restrictions on the agents. The formulation of the problem is: where \ ( c_ {ij} \) is the cost of assigning task j to agent i , \ ( a_ {ij} \) is the capacity used when ...
35 problem-solving techniques and methods for solving complex problems
6. Discovery & Action Dialogue (DAD) One of the best approaches is to create a safe space for a group to share and discover practices and behaviors that can help them find their own solutions. With DAD, you can help a group choose which problems they wish to solve and which approaches they will take to do so.
Operations Research with R
The assignment problem represents a special case of linear programming problem used for allocating resources (mostly workforce) in an optimal way; it is a highly useful tool for operation and project managers for optimizing costs. The lpSolve R package allows us to solve LP assignment problems with just very few lines of code.
Unbalanced Assignment Problem: Definition, Formulation, and Solution
The Unbalanced Assignment Problem is an extension of the Assignment Problem in OR, where the number of tasks and workers is not equal. In the UAP, some tasks may remain unassigned, while some workers may not be assigned any task. The objective is still to minimize the total cost or time required to complete the assigned tasks, but the UAP has ...
(PDF) Ones assignment method for solving assignment problems
In this paper, a new and simple metho d was introduced for solving assignment. problem. This method can b e used for all kinds of assignment problems, whether maximize or minimize ob jective ...
Types of Linear Programming Problems
Steps for Solving Linear Programming Problems. Step 1: Identify the decision variables: The first step is to determine which choice factors control the behaviour of the objective function. A function that needs to be optimised is an objective function. Determine the decision variables and designate them with X, Y, and Z symbols.
assignment problem
Solve the assignment problem with ease using the Hungarian method. Our comprehensive guide walks you through the steps to minimize costs and maximize profits. ... Learn about the different types of models used in Operations Research, their advantages and limitations, and how they are applied in real-world scenarios.
Solving Assignment Problems in Operations Research
1/5/2024 Operations Research 4 Simplex Method (ILP Model) Very tedious to solve the problem with many constraints & variables (artificial and decision variables). Transportation Method Severely degenerate (occupied cells < m+n-1). Assignment problem is a variation of transportation problem... 1. Cost matrix is a square matrix 2. Only one assignment in a given row/column Hungarian Assignment ...
Comparative study of typical neural solvers in solving math word problems
In recent years, there has been a significant increase in the design of neural network models for solving math word problems (MWPs). These neural solvers have been designed with various architectures and evaluated on diverse datasets, posing challenges in fair and effective performance evaluation. This paper presents a comparative study of representative neural solvers, aiming to elucidate ...
Data Science skills 101: How to solve any problem
The same but different. Source: author. Creating a separate but related problem can be a very effective technique in problem solving. It is particularly relevant where you have expertise/resources/skills in a particular area and want to exploit this.
4 Common Types of Team Conflict
The first occurs when conflict revolves around a single member of a team (20-25% of team conflicts). The second is when two members of a team disagree (the most common team conflict at 35%). The ...
International research team uses wavefunction matching to solve quantum
New approach makes calculations with realistic interactions possibleFRIB researchers are part of an international research team solving challenging computational problems in quantum physics using a new method called wavefunction matching. The new approach has applications to fields such as nuclear physics, where it is enabling theoretical calculations of atomic nuclei that were previously not ...