what is the statistical problem solving process

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons
• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

4.2: The Statistical Process

• Last updated
• Save as PDF
• Page ID 20849

• Maurice A. Geraghty
• De Anza College

Statistical Inference can be thought of as a process that can be used for testing claims and making estimates. 

Steps of a Statistical Process

Step 1 (Problem) :      Ask a question that can be answered with sample data.

Step 2 (Plan) :            Determine what information is needed.

Step 3 (Data) :            Collect sample data that is representative of the population.

Step 4 (Analysis) :      Summarize, interpret and analyze the sample data.

Step 5 (Conclusion) :  State the results and conclusion of the study.

In Step 3, we introduce the concept of a representative sample. Let’s define it here.

Definition: Representative sample

A representative sample has characteristics, behaviors and attitudes similar to the population from which the sample is selected.  

Definition: Biased sample

A sample that is not representative is a biased sample.

Representative samples are necessary to make valid claims about the population. We will explore methods of obtaining representative samples in a later section.

Example: Online dating trends

In 2015, the Pew Research Center Pew Research Center was investigating trends in online dating; this culminated in a study published in February, 2016. 41     Pew Research wanted to investigate a belief that American’s use of online dating website and mobile applications had increased from an earlier study done in 2013, especially among younger adults. 

A survey was conducted among a national sample of 2,001 adults, 18 years of age or older, living in all 50 U.S. states and the District of Columbia. Fully 701 respondents were interviewed on a landline telephone, and 1,300 were interviewed on a cell phone, including 749 who had no landline telephone. Calls were made using random digit dialing. In addition to questions about online dating, researchers collected demographic data as well (age, gender, ethnicity, etc).

The survey found that in 2015, 15% of American adults have used online dating sites and mobile apps, compared to 11% in 2013. However, for young adults aged 18‐24, the increase was dramatic: from 10% in 2013 to 27% in 2015. All age groups are summarized in the graph.

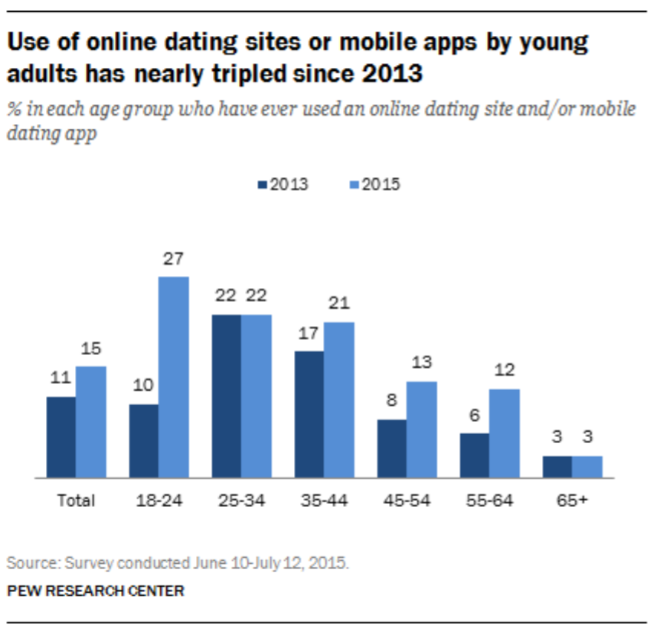
Let’s first identify the population and the sample in this study.

The population is all American adults living in all 50 states and the District of Columbia. The sample is the 2,001 adults surveyed.

In this example we can investigate how Pew Research Center followed the Steps of a Statistical Process in performing this analysis.  

How to Solve Statistical Problems Efficiently [Master Your Data Analysis Skills]

• November 17, 2023

Are you tired of feeling overstimulated by statistical problems? Welcome – you have now found the perfect article.

We understand the frustration that comes with trying to make sense of complex data sets.

Let’s work hand-in-hand to unpack those statistical secrets and find clarity in the numbers.

Do you find yourself stuck, unable to move forward because of statistical roadblocks? We’ve been there too. Our skill in solving statistical problems will help you find the way in through the toughest tough difficulties with confidence. Let’s tackle these problems hand-in-hand and pave the way to success.

As experts in the field, we know what it takes to conquer statistical problems effectively. This article is adjusted to meet your needs and provide you with the solutions you’ve been searching for. Join us on this voyage towards mastering statistics and unpack a world of possibilities.

Key Takeaways

• Data collection is the foundation of statistical analysis and must be accurate.
• Understanding descriptive and inferential statistics is critical for looking at and interpreting data effectively.
• Probability quantifies uncertainty and helps in making smart decisionss during statistical analysis.
• Identifying common statistical roadblocks like misinterpreting data or selecting inappropriate tests is important for effective problem-solving.
• Strategies like understanding the problem, choosing the right tools, and practicing regularly are key to tackling statistical tough difficulties.
• Using tools such as statistical software, graphing calculators, and online resources can aid in solving statistical problems efficiently.

Understanding Statistical Problems

When exploring the world of statistics, it’s critical to assimilate the nature of statistical problems. These problems often involve interpreting data, looking at patterns, and drawing meaningful endings. Here are some key points to consider:

• Data Collection: The foundation of statistical analysis lies in accurate data collection. Whether it’s surveys, experiments, or observational studies, gathering relevant data is important.
• Descriptive Statistics: Understanding descriptive statistics helps in summarizing and interpreting data effectively. Measures such as mean, median, and standard deviation provide useful ideas.
• Inferential Statistics: This branch of statistics involves making predictions or inferences about a population based on sample data. It helps us understand patterns and trends past the observed data.
• Probability: Probability is huge in statistical analysis by quantifying uncertainty. It helps us assess the likelihood of events and make smart decisionss.

To solve statistical problems proficiently, one must have a solid grasp of these key concepts.

By honing our statistical literacy and analytical skills, we can find the way in through complex data sets with confidence.

Let’s investigate more into the area of statistics and unpack its secrets.

Identifying Common Statistical Roadblocks

When tackling statistical problems, identifying common roadblocks is important to effectively find the way in the problem-solving process.

Let’s investigate some key problems individuals often encounter:

• Misinterpretation of Data: One of the primary tough difficulties is misinterpreting the data, leading to erroneous endings and flawed analysis.
• Selection of Appropriate Statistical Tests: Choosing the right statistical test can be perplexing, impacting the accuracy of results. It’s critical to have a solid understanding of when to apply each test.
• Assumptions Violation: Many statistical methods are based on certain assumptions. Violating these assumptions can skew results and mislead interpretations.

To overcome these roadblocks, it’s necessary to acquire a solid foundation in statistical principles and methodologies.

By honing our analytical skills and continuously improving our statistical literacy, we can adeptly address these tough difficulties and excel in statistical problem-solving.

For more ideas on tackling statistical problems, refer to this full guide on Common Statistical Errors .

Strategies for Tackling Statistical Tough difficulties

When facing statistical tough difficulties, it’s critical to employ effective strategies to find the way in through complex data analysis.

Here are some key approaches to tackle statistical problems:

• Understand the Problem: Before exploring analysis, ensure a clear comprehension of the statistical problem at hand.
• Choose the Right Tools: Selecting appropriate statistical tests is important for accurate results.
• Check Assumptions: Verify that the data meets the assumptions of the chosen statistical method to avoid skewed outcomes.
• Consult Resources: Refer to reputable sources like textbooks or online statistical guides for assistance.
• Practice Regularly: Improve statistical skills through consistent practice and application in various scenarios.
• Seek Guidance: When in doubt, seek advice from experienced statisticians or mentors.

By adopting these strategies, individuals can improve their problem-solving abilities and overcome statistical problems with confidence.

For further ideas on statistical problem-solving, refer to a full guide on Common Statistical Errors .

Tools for Solving Statistical Problems

When it comes to tackling statistical tough difficulties effectively, having the right tools at our disposal is important.

Here are some key tools that can aid us in solving statistical problems:

• Statistical Software: Using software like R or Python can simplify complex calculations and streamline data analysis processes.
• Graphing Calculators: These tools are handy for visualizing data and identifying trends or patterns.
• Online Resources: Websites like Kaggle or Stack Overflow offer useful ideas, tutorials, and communities for statistical problem-solving.
• Textbooks and Guides: Referencing textbooks such as “Introduction to Statistical Learning” or online guides can provide in-depth explanations and step-by-step solutions.

By using these tools effectively, we can improve our problem-solving capabilities and approach statistical tough difficulties with confidence.

For further ideas on common statistical errors to avoid, we recommend checking out the full guide on Common Statistical Errors For useful tips and strategies.

Putting in place Effective Solutions

When approaching statistical problems, it’s critical to have a strategic plan in place.

Here are some key steps to consider for putting in place effective solutions:

• Define the Problem: Clearly outline the statistical problem at hand to understand its scope and requirements fully.
• Collect Data: Gather relevant data sets from credible sources or conduct surveys to acquire the necessary information for analysis.
• Choose the Right Model: Select the appropriate statistical model based on the nature of the data and the specific question being addressed.
• Use Advanced Tools: Use statistical software such as R or Python to perform complex analyses and generate accurate results.
• Validate Results: Verify the accuracy of the findings through strict testing and validation procedures to ensure the reliability of the endings.

By following these steps, we can streamline the statistical problem-solving process and arrive at well-informed and data-driven decisions.

For further ideas and strategies on tackling statistical tough difficulties, we recommend exploring resources such as DataCamp That offer interactive learning experiences and tutorials on statistical analysis.

• Recent Posts

• How to Make a Relational Database [Boost Your Database Performance Now] - April 10, 2024
• How to Get a Job in Data Analysis [Expert Tips Inside] - April 10, 2024
• Do You Need Software to Use Xbox Controller on PC? [Discover the Best Method] - April 10, 2024

Trending now

Statistical Thinking for Industrial Problem Solving

A free online statistics course.

Back to Course Overview

Statistical Thinking and Problem Solving

Statistical thinking is vital for solving real-world problems. At the heart of statistical thinking is making decisions based on data. This requires disciplined approaches to identifying problems and the ability to quantify and interpret the variation that you observe in your data.

In this module, you will learn how to clearly define your problem and gain an understanding of the underlying processes that you will improve. You will learn techniques for identifying potential root causes of the problem. Finally, you will learn about different types of data and different approaches to data collection.

Estimated time to complete this module: 2 to 3 hours

Statistical Thinking and Problem Solving Overview (0:36)

Specific topics covered in this module include:

Statistical thinking.

• What is Statistical Thinking

Problem Solving

• Overview of Problem Solving
• Statistical Problem Solving
• Types of Problems
• Defining the Problem
• Goals and Key Performance Indicators
• The White Polymer Case Study

Defining the Process

• What is a Process?
• Developing a SIPOC Map
• Developing an Input/Output Process Map
• Top-Down and Deployment Flowcharts

Identifying Potential Root Causes

• Tools for Identifying Potential Causes
• Brainstorming
• Multi-voting
• Using Affinity Diagrams
• Cause-and-Effect Diagrams
• The Five Whys
• Cause-and-Effect Matrices

Compiling and Collecting Data

• Data Collection for Problem Solving
• Types of Data
• Operational Definitions
• Data Collection Strategies
• Importing Data for Analysis

ORIGINAL RESEARCH article

Statistical analysis of complex problem-solving process data: an event history analysis approach.

• 1 Department of Statistics, London School of Economics and Political Science, London, United Kingdom
• 2 School of Statistics, University of Minnesota, Minneapolis, MN, United States
• 3 Department of Statistics, Columbia University, New York, NY, United States

Complex problem-solving (CPS) ability has been recognized as a central 21st century skill. Individuals' processes of solving crucial complex problems may contain substantial information about their CPS ability. In this paper, we consider the prediction of duration and final outcome (i.e., success/failure) of solving a complex problem during task completion process, by making use of process data recorded in computer log files. Solving this problem may help answer questions like “how much information about an individual's CPS ability is contained in the process data?,” “what CPS patterns will yield a higher chance of success?,” and “what CPS patterns predict the remaining time for task completion?” We propose an event history analysis model for this prediction problem. The trained prediction model may provide us a better understanding of individuals' problem-solving patterns, which may eventually lead to a good design of automated interventions (e.g., providing hints) for the training of CPS ability. A real data example from the 2012 Programme for International Student Assessment (PISA) is provided for illustration.

1. Introduction

Complex problem-solving (CPS) ability has been recognized as a central 21st century skill of high importance for several outcomes including academic achievement ( Wüstenberg et al., 2012 ) and workplace performance ( Danner et al., 2011 ). It encompasses a set of higher-order thinking skills that require strategic planning, carrying out multi-step sequences of actions, reacting to a dynamically changing system, testing hypotheses, and, if necessary, adaptively coming up with new hypotheses. Thus, there is almost no doubt that an individual's problem-solving process data contain substantial amount of information about his/her CPS ability and thus are worth analyzing. Meaningful information extracted from CPS process data may lead to better understanding, measurement, and even training of individuals' CPS ability.

Problem-solving process data typically have a more complex structure than that of panel data which are traditionally more commonly encountered in statistics. Specifically, individuals may take different strategies toward solving the same problem. Even for individuals who take the same strategy, their actions and time-stamps of the actions may be very different. Due to such heterogeneity and complexity, classical regression and multivariate data analysis methods cannot be straightforwardly applied to CPS process data.

Possibly due to the lack of suitable analytic tools, research on CPS process data is limited. Among the existing works, none took a prediction perspective. Specifically, Greiff et al. (2015) presented a case study, showcasing the strong association between a specific strategic behavior (identified by expert knowledge) in a CPS task from the 2012 Programme for International Student Assessment (PISA) and performance both in this specific task and in the overall PISA problem-solving score. He and von Davier (2015 , 2016) proposed an N-gram method from natural language processing for analyzing problem-solving items in technology-rich environments, focusing on identifying feature sequences that are important to task completion. Vista et al. (2017) developed methods for the visualization and exploratory analysis of students' behavioral pathways, aiming to detect action sequences that are potentially relevant for establishing particular paths as meaningful markers of complex behaviors. Halpin and De Boeck (2013) and Halpin et al. (2017) adopted a Hawkes process approach to analyzing collaborative problem-solving items, focusing on the psychological measurement of collaboration. Xu et al. (2018) proposed a latent class model that analyzes CPS patterns by classifying individuals into latent classes based on their problem-solving processes.

In this paper, we propose to analyze CPS process data from a prediction perspective. As suggested in Yarkoni and Westfall (2017) , an increased focus on prediction can ultimately lead us to greater understanding of human behavior. Specifically, we consider the simultaneous prediction of the duration and the final outcome (i.e., success/failure) of solving a complex problem based on CPS process data. Instead of a single prediction, we hope to predict at any time during the problem-solving process. Such a data-driven prediction model may bring us insights about individuals' CPS behavioral patterns. First, features that contribute most to the prediction may correspond to important strategic behaviors that are key to succeeding in a task. In this sense, the proposed method can be used as an exploratory data analysis tool for extracting important features from process data. Second, the prediction accuracy may also serve as a measure of the strength of the signal contained in process data that reflects one's CPS ability, which reflects the reliability of CPS tasks from a prediction perspective. Third, for low stake assessments, the predicted chance of success may be used to give partial credits when scoring task takers. Fourth, speed is another important dimension of complex problem solving that is closely associated with the final outcome of task completion ( MacKay, 1982 ). The prediction of the duration throughout the problem-solving process may provide us insights on the relationship between the CPS behavioral patterns and the CPS speed. Finally, the prediction model also enables us to design suitable interventions during their problem-solving processes. For example, a hint may be provided when a student is predicted having a high chance to fail after sufficient efforts.

More precisely, we model the conditional distribution of duration time and final outcome given the event history up to any time point. This model can be viewed as a special event history analysis model, a general statistical framework for analyzing the expected duration of time until one or more events happen (see e.g., Allison, 2014 ). The proposed model can be regarded as an extension to the classical regression approach. The major difference is that the current model is specified over a continuous-time domain. It consists of a family of conditional models indexed by time, while the classical regression approach does not deal with continuous-time information. As a result, the proposed model supports prediction at any time during one's problem-solving process, while the classical regression approach does not. The proposed model is also related to, but substantially different from response time models (e.g., van der Linden, 2007 ) which have received much attention in psychometrics in recent years. Specifically, response time models model the joint distribution of response time and responses to test items, while the proposed model focuses on the conditional distribution of CPS duration and final outcome given the event history.

Although the proposed method learns regression-type models from data, it is worth emphasizing that we do not try to make statistical inference, such as testing whether a specific regression coefficient is significantly different from zero. Rather, the selection and interpretation of the model are mainly justified from a prediction perspective. This is because statistical inference tends to draw strong conclusions based on strong assumptions on the data generation mechanism. Due to the complexity of CPS process data, a statistical model may be severely misspecified, making valid statistical inference a big challenge. On the other hand, the prediction framework requires less assumptions and thus is more suitable for exploratory analysis. More precisely, the prediction framework admits the discrepancy between the underlying complex data generation mechanism and the prediction model ( Yarkoni and Westfall, 2017 ). A prediction model aims at achieving a balance between the bias due to this discrepancy and the variance due to a limited sample size. As a price, findings from the predictive framework are preliminary and only suggest hypotheses for future confirmatory studies.

The rest of the paper is organized as follows. In Section 2, we describe the structure of complex problem-solving process data and then motivate our research questions, using a CPS item from PISA 2012 as an example. In Section 3, we formulate the research questions under a statistical framework, propose a model, and then provide details of estimation and prediction. The introduced model is illustrated through an application to an example item from PISA 2012 in Section 4. We discuss limitations and future directions in Section 5.

2. Complex Problem-Solving Process Data

2.1. a motivating example.

We use a specific CPS item, CLIMATE CONTROL (CC) 1 , to demonstrate the data structure and to motivate our research questions. It is part of a CPS unit in PISA 2012 that was designed under the “MicroDYN” framework ( Greiff et al., 2012 ; Wüstenberg et al., 2012 ), a framework for the development of small dynamic systems of causal relationships for assessing CPS.

In this item, students are instructed to manipulate the panel (i.e., to move the top, central, and bottom control sliders; left side of Figure 1A ) and to answer how the input variables (control sliders) are related to the output variables (temperature and humidity). Specifically, the initial position of each control slider is indicated by a triangle “▴.” The students can change the top, central and bottom controls on the left of Figure 1 by using the sliders. By clicking “APPLY,” they will see the corresponding changes in temperature and humidity. After exploration, the students are asked to draw lines in a diagram ( Figure 1B ) to answer what each slider controls. The item is considered correctly answered if the diagram is correctly completed. The problem-solving process for this item is that the students must experiment to determine which controls have an impact on temperature and which on humidity, and then represent the causal relations by drawing arrows between the three inputs (top, central, and bottom control sliders) and the two outputs (temperature and humidity).

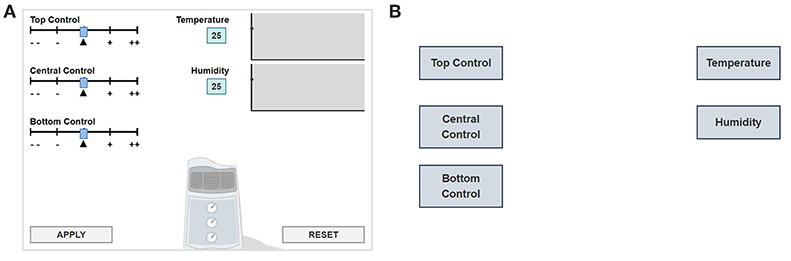
Figure 1. (A) Simulation environment of CC item. (B) Answer diagram of CC item.

PISA 2012 collected students' problem-solving process data in computer log files, in the form of a sequence of time-stamped events. We illustrate the structure of data in Table 1 and Figure 2 , where Table 1 tabulates a sequence of time-stamped events from a student and Figure 2 visualizes the corresponding event time points on a time line. According to the data, 14 events were recorded between time 0 (start) and 61.5 s (success). The first event happened at 29.5 s that was clicking “APPLY” after the top, central, and bottom controls were set at 2, 0, and 0, respectively. A sequence of actions followed the first event and finally at 58, 59.1, and 59.6 s, a final answer was correctly given using the diagram. It is worth clarifying that this log file does not collect all the interactions between a student and the simulated system. That is, the status of the control sliders is only recorded in the log file, when the “APPLY” button is clicked.

Table 1 . An example of computer log file data from CC item in PISA 2012.

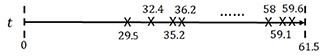
Figure 2 . Visualization of the structure of process data from CC item in PISA 2012.

The process data for solving a CPS item typically have two components, knowledge acquisition and knowledge application, respectively. This CC item mainly focuses the former, which includes learning the causal relationships between the inputs and the outputs and representing such relationships by drawing the diagram. Since data on representing the causal relationship is relatively straightforward, in the rest of the paper, we focus on the process data related to knowledge acquisition and only refer a student's problem-solving process to his/her process of exploring the air conditioner, excluding the actions involving the answer diagram.

Intuitively, students' problem-solving processes contain information about their complex problem-solving ability, whether in the context of the CC item or in a more general sense of dealing with complex tasks in practice. However, it remains a challenge to extract meaningful information from their process data, due to the complex data structure. In particular, the occurrences of events are heterogeneous (i.e., different people can have very different event histories) and unstructured (i.e., there is little restriction on the order and time of the occurrences). Different students tend to have different problem-solving trajectories, with different actions taken at different time points. Consequently, time series models, which are standard statistical tools for analyzing dynamic systems, are not suitable here.

2.2. Research Questions

We focus on two specific research questions. Consider an individual solving a complex problem. Given that the individual has spent t units of time and has not yet completed the task, we would like to ask the following two questions based on the information at time t : How much additional time does the individual need? And will the individual succeed or fail upon the time of task completion?

Suppose we index the individual by i and let T i be the total time of task completion and Y i be the final outcome. Moreover, we denote H i ( t ) = ( h i 1 ( t ) , ... , h i p ( t ) ) ⊤ as a p -vector function of time t , summarizing the event history of individual i from the beginning of task to time t . Each component of H i ( t ) is a feature constructed from the event history up to time t . Taking the above CC item as an example, components of H i ( t ) may be, the number of actions a student has taken, whether all three control sliders have been explored, the frequency of using the reset button, etc., up to time t . We refer to H i ( t ) as the event history process of individual i . The dimension p may be high, depending on the complexity of the log file.

With the above notation, the two questions become to simultaneously predict T i and Y i based on H i ( t ). Throughout this paper, we focus on the analysis of data from a single CPS item. Extensions of the current framework to multiple-item analysis are discussed in Section 5.

3. Proposed Method

3.1. a regression model.

We now propose a regression model to answer the two questions raised in Section 2.2. We specify the marginal conditional models of Y i and T i given H i ( t ) and T i > t , respectively. Specifically, we assume

where Φ is the cumulative distribution function of a standard normal distribution. That is, Y i is assumed to marginally follow a probit regression model. In addition, only the conditional mean and variance are assumed for log( T i − t ). Our model parameters include the regression coefficients B = ( b jk )2 × p and conditional variance σ 2 . Based on the above model specification, a pseudo-likelihood function will be devived in Section 3.3 for parameter estimation.

Although only marginal models are specified, we point out that the model specifications (1) through (3) impose quite strong assumptions. As a result, the model may not most closely approximate the data-generating process and thus a bias is likely to exist. On the other hand, however, it is a working model that leads to reasonable prediction and can be used as a benchmark model for this prediction problem in future investigations.

We further remark that the conditional variance of log( T i − t ) is time-invariant under the current specification, which can be further relaxed to be time-dependent. In addition, the regression model for response time is closely related to the log-normal model for response time analysis in psychometrics (e.g., van der Linden, 2007 ). The major difference is that the proposed model is not a measurement model disentangling item and person effects on T i and Y i .

3.2. Prediction

Under the model in Section 3.1, given the event history, we predict the final outcome based on the success probability Φ( b 11 h i 1 ( t ) + ⋯ + b 1 p h ip ( t )). In addition, based on the conditional mean of log( T i − t ), we predict the total time at time t by t + exp( b 21 h i 1 ( t ) + ⋯ + b 2 p h ip ( t )). Given estimates of B from training data, we can predict the problem-solving duration and final outcome at any t for an individual in the testing sample, throughout his/her entire problem-solving process.

3.3. Parameter Estimation

It remains to estimate the model parameters based on a training dataset. Let our data be (τ i , y i ) and { H i ( t ): t ≥ 0}, i = 1, …, N , where τ i and y i are realizations of T i and Y i , and { H i ( t ): t ≥ 0} is the entire event history.

We develop estimating equations based on a pseudo likelihood function. Specifically, the conditional distribution of Y i given H i ( t ) and T i > t can be written as

where b 2 = ( b 11 , ... , b 1 p ) ⊤ . In addition, using the log-normal model as a working model for T i − t , the corresponding conditional distribution of T i can be written as

where b 2 = ( b 21 , ... , b 2 p ) ⊤ . The pseudo-likelihood is then written as

where t 1 , …, t J are J pre-specified grid points that spread out over the entire time spectrum. The choice of the grid points will be discussed in the sequel. By specifying the pseudo-likelihood based on the sequence of time points, the prediction at different time is taken into accounting in the estimation. We estimate the model parameters by maximizing the pseudo-likelihood function L ( B , σ).

In fact, (5) can be factorized into

Therefore, b 1 is estimated by maximizing L 1 ( b 1 ), which takes the form of a likelihood function for probit regression. Similarly, b 2 and σ are estimated by maximizing L 2 ( b 2 , σ), which is equivalent to solving the following estimation equations,

The estimating equations (8) and (9) can also be derived directly based on the conditional mean and variance specification of log( T i − t ). Solving these equations is equivalent to solving a linear regression problem, and thus is computationally easy.

3.4. Some Remarks

We provide a few remarks. First, choosing suitable features into H i ( t ) is important. The inclusion of suitable features not only improves the prediction accuracy, but also facilitates the exploratory analysis and interpretation of how behavioral patterns affect CPS result. If substantive knowledge about a CPS task is available from cognition theory, one may choose features that indicate different strategies toward solving the task. Otherwise, a data-driven approach may be taken. That is, one may select a model from a candidate list based on certain cross-validation criteria, where, if possible, all reasonable features should be consider as candidates. Even when a set of features has been suggested by cognition theory, one can still take the data-driven approach to find additional features, which may lead to new findings.

Second, one possible extension of the proposed model is to allow the regression coefficients to be a function of time t , whereas they are independent of time under the current model. In that case, the regression coefficients become functions of time, b jk ( t ). The current model can be regarded as a special case of this more general model. In particular, if b jk ( t ) has high variation along time in the best predictive model, then simply applying the current model may yield a high bias. Specifically, in the current estimation procedure, a larger grid point tends to have a smaller sample size and thus contributes less to the pseudo-likelihood function. As a result, a larger bias may occur in the prediction at a larger time point. However, the estimation of the time-dependent coefficient is non-trivial. In particular, constraints should be imposed on the functional form of b jk ( t ) to ensure a certain level of smoothness over time. As a result, b jk ( t ) can be accurately estimated using information from a finite number of time points. Otherwise, without any smoothness assumptions, to predict at any time during one's problem-solving process, there are an infinite number of parameters to estimate. Moreover, when a regression coefficient is time-dependent, its interpretation becomes more difficult, especially if the sign changes over time.

Third, we remark on the selection of grid points in the estimation procedure. Our model is specified in a continuous time domain that supports prediction at any time point in a continuum during an individual's problem-solving process. The use of discretized grid points is a way to approximate the continuous-time system, so that estimation equations can be written down. In practice, we suggest to place the grid points based on the quantiles of the empirical distribution of duration based on the training set. See the analysis in Section 4 for an illustration. The number of grid points may be further selected by cross validation. We also point out that prediction can be made at any time point on the continuum, not limited to the grid points for parameter estimation.

4. An Example from PISA 2012

4.1. background.

In what follows, we illustrate the proposed method via an application to the above CC item 2 . This item was also analyzed in Greiff et al. (2015) and Xu et al. (2018) . The dataset was cleaned from the entire released dataset of PISA 2012. It contains 16,872 15-year-old students' problem-solving processes, where the students were from 42 countries and economies. Among these students, 54.5% answered correctly. On average, each student took 129.9 s and 17 actions solving the problem. Histograms of the students' problem-solving duration and number of actions are presented in Figure 3 .

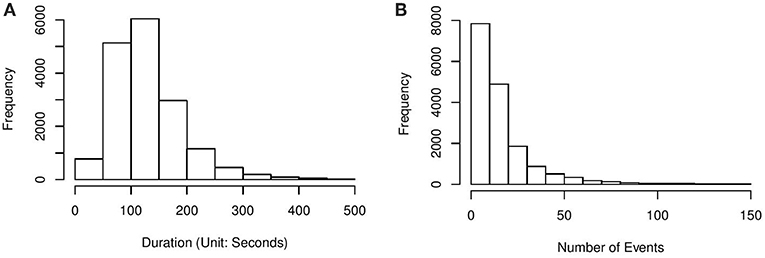
Figure 3. (A) Histogram of problem-solving duration of the CC item. (B) Histogram of the number of actions for solving the CC item.

4.2. Analyses

The entire dataset was randomly split into training and testing sets, where the training set contains data from 13,498 students and the testing set contains data from 3,374 students. A predictive model was built solely based on the training set and then its performance was evaluated based on the testing set. We used J = 9 grid points for the parameter estimation, with t 1 through t 9 specified to be 64, 81, 94, 106, 118, 132, 149, 170, and 208 s, respectively, which are the 10% through 90% quantiles of the empirical distribution of duration. As discussed earlier, the number of grid points and their locations may be further engineered by cross validation.

4.2.1. Model Selection

We first build a model based on the training data, using a data-driven stepwise forward selection procedure. In each step, we add one feature into H i ( t ) that leads to maximum increase in a cross-validated log-pseudo-likelihood, which is calculated based on a five-fold cross validation. We stop adding features into H i ( t ) when the cross-validated log-pseudo-likelihood stops increasing. The order in which the features are added may serve as a measure of their contribution to predicting the CPS duration and final outcome.

The candidate features being considered for model selection are listed in Table 2 . These candidate features were chosen to reflect students' CPS behavioral patterns from different aspects. In what follows, we discuss some of them. For example, the feature I i ( t ) indicates whether or not all three control sliders have been explored by simple actions (i.e., moving one control slider at a time) up to time t . That is, I i ( t ) = 1 means that the vary-one-thing-at-a-time (VOTAT) strategy ( Greiff et al., 2015 ) has been taken. According to the design of the CC item, the VOTAT strategy is expected to be a strong predictor of task success. In addition, the feature N i ( t )/ t records a student's average number of actions per unit time. It may serve as a measure of the student's speed of taking actions. In experimental psychology, response time or equivalently speed has been a central source for inferences about the organization and structure of cognitive processes (e.g., Luce, 1986 ), and in educational psychology, joint analysis of speed and accuracy of item response has also received much attention in recent years (e.g., van der Linden, 2007 ; Klein Entink et al., 2009 ). However, little is known about the role of speed in CPS tasks. The current analysis may provide some initial result on the relation between a student's speed and his/her CPS performance. Moreover, the features defined by the repeating of previously taken actions may reflect students' need of verifying the derived hypothesis on the relation based on the previous action or may be related to students' attention if the same actions are repeated many times. We also include 1, t, t 2 , and t 3 in H i ( t ) as the initial set of features to capture the time effect. For simplicity, country information is not taken into account in the current analysis.

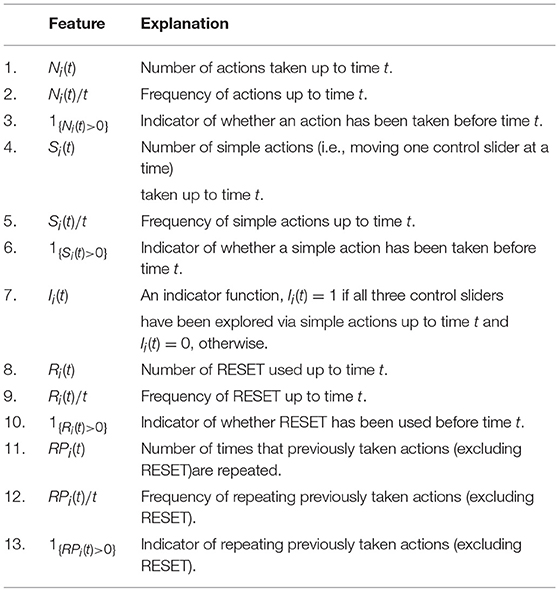
Table 2 . The list of candidate features to be incorporated into the model.

Our results on model selection are summarized in Figure 4 and Table 3 . The pseudo-likelihood stopped increasing after 11 steps, resulting a final model with 15 components in H i ( t ). As we can see from Figure 4 , the increase in the cross-validated log-pseudo-likelihood is mainly contributed by the inclusion of features in the first six steps, after which the increment is quite marginal. As we can see, the first, second, and sixth features entering into the model are all related to taking simple actions, a strategy known to be important to this task (e.g., Greiff et al., 2015 ). In particular, the first feature being selected is I i ( t ), which confirms the strong effect of the VOTAT strategy. In addition, the third and fourth features are both based on N i ( t ), the number of actions taken before time t . Roughly, the feature 1 { N i ( t )>0} reflects the initial planning behavior ( Eichmann et al., 2019 ). Thus, this feature tends to measure students' speed of reading the instruction of the item. As discussed earlier, the feature N i ( t )/ t measures students' speed of taking actions. Finally, the fifth feature is related to the use of the RESET button.

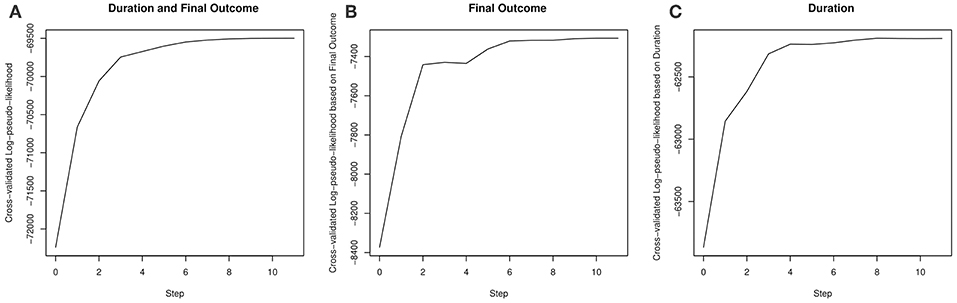
Figure 4 . The increase in the cross-validated log-pseudo-likelihood based on a stepwise forward selection procedure. (A–C) plot the cross-validated log-pseudo-likelihood, corresponding to L ( B , σ), L 1 ( b 1 ), L 2 ( b 2 , σ), respectively.

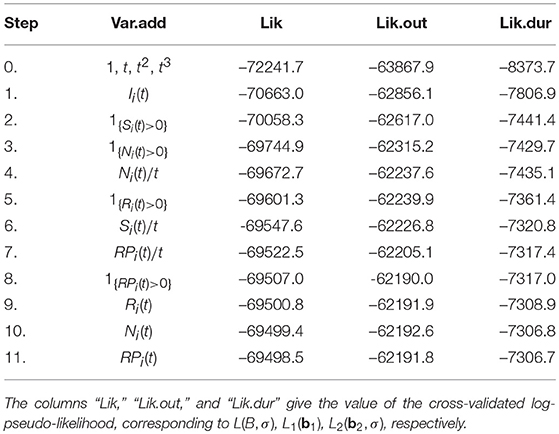
Table 3 . Results on model selection based on a stepwise forward selection procedure.

4.2.2. Prediction Performance on Testing Set

We now look at the prediction performance of the above model on the testing set. The prediction performance was evaluated at a larger set of time points from 19 to 281 s. Instead of reporting based on the pseudo-likelihood function, we adopted two measures that are more straightforward. Specifically, we measured the prediction of final outcome by the Area Under the Curve (AUC) of the predicted Receiver Operating Characteristic (ROC) curve. The value of AUC is between 0 and 1. A larger AUC value indicates better prediction of the binary final outcome, with AUC = 1 indicating perfect prediction. In addition, at each time point t , we measured the prediction of duration based on the root mean squared error (RMSE), defined as

where τ i , i = N + 1, …, N + n , denotes the duration of students in the testing set, and τ ^ i ( t ) denotes the prediction based on information up to time t according to the trained model.

Results are presented in Figure 5 , where the testing AUC and RMSE for the final outcome and duration are presented. In particular, results based on the model selected by cross validation ( p = 15) and the initial model ( p = 4, containing the initial covariates 1, t , t 2 , and t 3 ) are compared. First, based on the selected model, the AUC is never above 0.8 and the RMSE is between 53 and 64 s, indicating a low signal-to-noise ratio. Second, the students' event history does improve the prediction of final outcome and duration upon the initial model. Specifically, since the initial model does not take into account the event history, it predicts the students with duration longer than t to have the same success probability. Consequently, the test AUC is 0.5 at each value of t , which is always worse than the performance of the selected model. Moreover, the selected model always outperforms the initial model in terms of the prediction of duration. Third, the AUC for the prediction of the final outcome is low when t is small. It keeps increasing as time goes on and fluctuates around 0.72 after about 120 s.

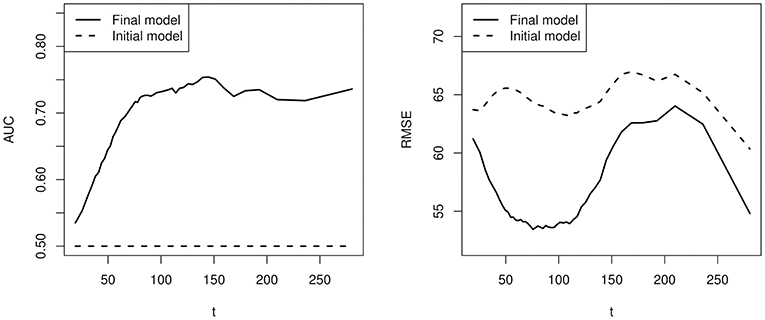
Figure 5 . A comparison of prediction accuracy between the model selected by cross validation and a baseline model without using individual specific event history.

4.2.3. Interpretation of Parameter Estimates

To gain more insights into how the event history affects the final outcome and duration, we further look at the results of parameter estimation. We focus on a model whose event history H i ( t ) includes the initial features and the top six features selected by cross validation. This model has similar prediction accuracy as the selected model according to the cross-validation result in Figure 4 , but contains less features in the event history and thus is easier to interpret. Moreover, the parameter estimates under this model are close to those under the cross-validation selected model, and the signs of the regression coefficients remain the same.

The estimated regression coefficients are presented in Table 4 . First, the first selected feature I i ( t ), which indicates whether all three control sliders have been explored via simple actions, has a positive regression coefficient on final outcome and a negative coefficient on duration. It means that, controlling the rest of the parameters, a student who has taken the VOTAT strategy tends to be more likely to give a correct answer and to complete in a shorter period of time. This confirms the strong effect of VOTAT strategy in solving the current task.

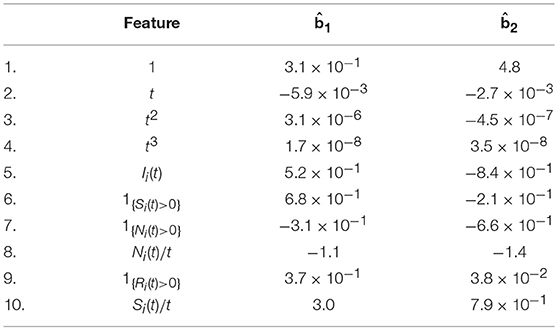
Table 4 . Estimated regression coefficients for a model for which the event history process contains the initial features based on polynomials of t and the top six features selected by cross validation.

Second, besides I i ( t ), there are two features related to taking simple actions, 1 { S i ( t )>0} and S i ( t )/ t , which are the indicator of taking at least one simple action and the frequency of taking simple actions. Both features have positive regression coefficients on the final outcome, implying larger values of both features lead to a higher success rate. In addition, 1 { S i ( t )>0} has a negative coefficient on duration and S i ( t )/ t has a positive one. Under this estimated model, the overall simple action effect on duration is b ^ 25 I i ( t ) + b ^ 26 1 { S i ( t ) > 0 } + b ^ 2 , 10 S i ( t ) / t , which is negative for most students. It implies that, overall, taking simple actions leads to a shorter predicted duration. However, once all three types of simple actions have been taken, a higher frequency of taking simple actions leads to a weaker but sill negative simple action effect on the duration.

Third, as discussed earlier, 1 { N i ( t )>0} tends to measure the student's speed of reading the instruction of the task and N i ( t )/ t can be regarded as a measure of students' speed of taking actions. According to the estimated regression coefficients, the data suggest that a student who reads and acts faster tends to complete the task in a shorter period of time with a lower accuracy. Similar results have been seen in the literature of response time analysis in educational psychology (e.g., Klein Entink et al., 2009 ; Fox and Marianti, 2016 ; Zhan et al., 2018 ), where speed of item response was found to negatively correlated with accuracy. In particular, Zhan et al. (2018) found a moderate negative correlation between students' general mathematics ability and speed under a psychometric model for PISA 2012 computer-based mathematics data.

Finally, 1 { R i ( t )>0} , the use of the RESET button, has positive regression coefficients on both final outcome and duration. It implies that the use of RESET button leads to a higher predicted success probability and a longer duration time, given the other features controlled. The connection between the use of the RESET button and the underlying cognitive process of complex problem solving, if it exists, still remains to be investigated.

5. Discussions

5.1. summary.

As an early step toward understanding individuals' complex problem-solving processes, we proposed an event history analysis method for the prediction of the duration and the final outcome of solving a complex problem based on process data. This approach is able to predict at any time t during an individual's problem-solving process, which may be useful in dynamic assessment/learning systems (e.g., in a game-based assessment system). An illustrative example is provided that is based on a CPS item from PISA 2012.

5.2. Inference, Prediction, and Interpretability

As articulated previously, this paper focuses on a prediction problem, rather than a statistical inference problem. Comparing with a prediction framework, statistical inference tends to draw stronger conclusions under stronger assumptions on the data generation mechanism. Unfortunately, due to the complexity of CPS process data, such assumptions are not only hardly satisfied, but also difficult to verify. On the other hand, a prediction framework requires less assumptions and thus is more suitable for exploratory analysis. As a price, the findings from the predictive framework are preliminary and can only be used to generate hypotheses for future studies.

It may be useful to provide uncertainty measures for the prediction performance and for the parameter estimates, where the former indicates the replicability of the prediction performance and the later reflects the stability of the prediction model. In particular, patterns from a prediction model with low replicability and low stability should not be overly interpreted. Such uncertainty measures may be obtained from cross validation and bootstrapping (see Chapter 7, Friedman et al., 2001 ).

It is also worth distinguishing prediction methods based on a simple model like the one proposed above and those based on black-box machine learning algorithms (e.g., random forest). Decisions based on black-box algorithms can be very difficult to understood by human and thus do not provide us insights about the data, even though they may have a high prediction accuracy. On the other hand, a simple model can be regarded as a data dimension reduction tool that extracts interpretable information from data, which may facilitate our understanding of complex problem solving.

5.3. Extending the Current Model

The proposed model can be extended along multiple directions. First, as discussed earlier, we may extend the model by allowing the regression coefficients b jk to be time-dependent. In that case, nonparametric estimation methods (e.g., splines) need to be developed for parameter estimation. In fact, the idea of time-varying coefficients has been intensively investigated in the event history analysis literature (e.g., Fan et al., 1997 ). This extension will be useful if the effects of the features in H i ( t ) change substantially over time.

Second, when the dimension p of H i ( t ) is high, better interpretability and higher prediction power may be achieved by using Lasso-type sparse estimators (see e.g., Chapter 3 Friedman et al., 2001 ). These estimators perform simultaneous feature selection and regularization in order to enhance the prediction accuracy and interpretability.

Finally, outliers are likely to occur in the data due to the abnormal behavioral patterns of a small proportion of people. A better treatment of outliers will lead to better prediction performance. Thus, a more robust objective function will be developed for parameter estimation, by borrowing ideas from the literature of robust statistics (see e.g., Huber and Ronchetti, 2009 ).

5.4. Multiple-Task Analysis

The current analysis focuses on analyzing data from a single task. To study individuals' CPS ability, it may be of more interest to analyze multiple CPS tasks simultaneously and to investigate how an individual's process data from one or multiple tasks predict his/her performance on the other tasks. Generally speaking, one's CPS ability may be better measured by the information in the process data that is generalizable across a representative set of CPS tasks than only his/her final outcomes on these tasks. In this sense, this cross-task prediction problem is closely related to the measurement of CPS ability. This problem is also worth future investigation.

Author Contributions

All authors listed have made a substantial, direct and intellectual contribution to the work, and approved it for publication.

This research was funded by NAEd/Spencer postdoctoral fellowship, NSF grant DMS-1712657, NSF grant SES-1826540, NSF grant IIS-1633360, and NIH grant R01GM047845.

Conflict of Interest Statement

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

1. ^ The item can be found on the OECD website ( http://www.oecd.org/pisa/test-2012/testquestions/question3/ )

2. ^ The log file data and code book for the CC item can be found online: http://www.oecd.org/pisa/pisaproducts/database-cbapisa2012.htm .

Allison, P. D. (2014). Event history analysis: Regression for longitudinal event data . London: Sage.

Google Scholar

Danner, D., Hagemann, D., Schankin, A., Hager, M., and Funke, J. (2011). Beyond IQ: a latent state-trait analysis of general intelligence, dynamic decision making, and implicit learning. Intelligence 39, 323–334. doi: 10.1016/j.intell.2011.06.004

CrossRef Full Text | Google Scholar

Eichmann, B., Goldhammer, F., Greiff, S., Pucite, L., and Naumann, J. (2019). The role of planning in complex problem solving. Comput. Educ . 128, 1–12. doi: 10.1016/j.compedu.2018.08.004

Fan, J., Gijbels, I., and King, M. (1997). Local likelihood and local partial likelihood in hazard regression. Anna. Statist . 25, 1661–1690. doi: 10.1214/aos/1031594736

Fox, J.-P., and Marianti, S. (2016). Joint modeling of ability and differential speed using responses and response times. Multivar. Behav. Res . 51, 540–553. doi: 10.1080/00273171.2016.1171128

PubMed Abstract | CrossRef Full Text | Google Scholar

Friedman, J., Hastie, T., and Tibshirani, R. (2001). The Elements of Statistical Learning . New York, NY: Springer.

Greiff, S., Wüstenberg, S., and Avvisati, F. (2015). Computer-generated log-file analyses as a window into students' minds? A showcase study based on the PISA 2012 assessment of problem solving. Comput. Educ . 91, 92–105. doi: 10.1016/j.compedu.2015.10.018

Greiff, S., Wüstenberg, S., and Funke, J. (2012). Dynamic problem solving: a new assessment perspective. Appl. Psychol. Measur . 36, 189–213. doi: 10.1177/0146621612439620

Halpin, P. F., and De Boeck, P. (2013). Modelling dyadic interaction with Hawkes processes. Psychometrika 78, 793–814. doi: 10.1007/s11336-013-9329-1

Halpin, P. F., von Davier, A. A., Hao, J., and Liu, L. (2017). Measuring student engagement during collaboration. J. Educ. Measur . 54, 70–84. doi: 10.1111/jedm.12133

He, Q., and von Davier, M. (2015). “Identifying feature sequences from process data in problem-solving items with N-grams,” in Quantitative Psychology Research , eds L. van der Ark, D. Bolt, W. Wang, J. Douglas, and M. Wiberg, (New York, NY: Springer), 173–190.

He, Q., and von Davier, M. (2016). “Analyzing process data from problem-solving items with n-grams: insights from a computer-based large-scale assessment,” in Handbook of Research on Technology Tools for Real-World Skill Development , eds Y. Rosen, S. Ferrara, and M. Mosharraf (Hershey, PA: IGI Global), 750–777.

Huber, P. J., and Ronchetti, E. (2009). Robust Statistics . Hoboken, NJ: John Wiley & Sons.

Klein Entink, R. H., Kuhn, J.-T., Hornke, L. F., and Fox, J.-P. (2009). Evaluating cognitive theory: A joint modeling approach using responses and response times. Psychol. Methods 14, 54–75. doi: 10.1037/a0014877

Luce, R. D. (1986). Response Times: Their Role in Inferring Elementary Mental Organization . New York, NY: Oxford University Press.

MacKay, D. G. (1982). The problems of flexibility, fluency, and speed–accuracy trade-off in skilled behavior. Psychol. Rev . 89, 483–506. doi: 10.1037/0033-295X.89.5.483

van der Linden, W. J. (2007). A hierarchical framework for modeling speed and accuracy on test items. Psychometrika 72, 287–308. doi: 10.1007/s11336-006-1478-z

Vista, A., Care, E., and Awwal, N. (2017). Visualising and examining sequential actions as behavioural paths that can be interpreted as markers of complex behaviours. Comput. Hum. Behav . 76, 656–671. doi: 10.1016/j.chb.2017.01.027

Wüstenberg, S., Greiff, S., and Funke, J. (2012). Complex problem solving–More than reasoning? Intelligence 40, 1–14. doi: 10.1016/j.intell.2011.11.003

Xu, H., Fang, G., Chen, Y., Liu, J., and Ying, Z. (2018). Latent class analysis of recurrent events in problem-solving items. Appl. Psychol. Measur . 42, 478–498. doi: 10.1177/0146621617748325

Yarkoni, T., and Westfall, J. (2017). Choosing prediction over explanation in psychology: lessons from machine learning. Perspect. Psychol. Sci . 12, 1100–1122. doi: 10.1177/1745691617693393

Zhan, P., Jiao, H., and Liao, D. (2018). Cognitive diagnosis modelling incorporating item response times. Br. J. Math. Statist. Psychol . 71, 262–286. doi: 10.1111/bmsp.12114

Keywords: process data, complex problem solving, PISA data, response time, event history analysis

Citation: Chen Y, Li X, Liu J and Ying Z (2019) Statistical Analysis of Complex Problem-Solving Process Data: An Event History Analysis Approach. Front. Psychol . 10:486. doi: 10.3389/fpsyg.2019.00486

Received: 31 August 2018; Accepted: 19 February 2019; Published: 18 March 2019.

Reviewed by:

Copyright © 2019 Chen, Li, Liu and Ying. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY) . The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.

*Correspondence: Yunxiao Chen, [email protected]

Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.

Have questions? Contact us at (770) 518-9967 or [email protected]

Statistical Problem Solving (SPS)

• Statistical Problem Solving

Problem solving in any organization is a problem. Nobody wants to own the responsibility for a problem and that is the reason, when a problem shows up fingers may be pointing at others rather than self.

This is a natural human instinctive defense mechanism and hence cannot hold it against any one. However, it is to be realized the problems in industry are real and cannot be wished away, solution must be sought either by hunch or by scientific methods. Only a systematic disciplined approach for defining and solving problems consistently and effectively reveal the real nature of a problem and the best possible solutions .

A Chinese proverb says, “ it is cheap to do guesswork for solution, but a wrong guess can be very expensive”. This is to emphasize that although occasional success is possible trough hunches gained through long years of experience in doing the same job, but a lasting solution is possible only through scientific methods.

One of the major scientific method for problem solving is through Statistical Problem Solving (SPS) this method is aimed at not only solving problems but may be used for improvement on existing situation. It involves a team armed with process and product knowledge, having willingness to work together as a team, can undertake selection of some statistical methods, have willingness to adhere to principles of economy and willingness to learn along the way.

Statistical Problem Solving (SPS) could be used for process control or product control. In many situations, the product would be customer dictated, tried, tested and standardized in the facility may involve testing at both internal to facility or external to facility may be complex and may require customer approval for changes which could be time consuming and complex. But if the problem warrants then this should be taken up. 

Process controls are lot simpler than product control where SPS may be used effectively for improving profitability of the industry, by reducing costs and possibly eliminating all 7 types of waste through use of Kaizen and lean management techniques.

The following could be used as 7 steps for Statistical Problem Solving (SPS)

• Defining the problem
• Listing variables
• Prioritizing variables
• Evaluating top few variables
• Optimizing variable settings
• Monitor and Measure results
• Reward/Recognize Team members

Defining the problem: Source for defining the problem could be from customer complaints, in-house rejections, observations by team lead or supervisor or QC personnel, levels of waste generated or such similar factors.

Listing and prioritizing variables involves all features associated with the processes. Example temperature, feed and speed of the machine, environmental factors, operator skills etc. It may be difficult to try and find solution for all variables together. Hence most probable variables are to be selected based on collective wisdom and experience of the team attempting to solve the problem.

Collection of data: Most common method in collecting data is the X bar and R charts.  Time is used as the variable in most cases and plotted on X axis, and other variables such as dimensions etc. are plotted graphically as shown in example below.

Once data is collected based on probable list of variables, then the data is brought to the attention of the team for brainstorming on what variables are to be controlled and how solution could be obtained. In other words , optimizing variables settings . Based on the brainstorming session process control variables are evaluated using popular techniques like “5 why”, “8D”, “Pareto Analysis”, “Ishikawa diagram”, “Histogram” etc. The techniques are used to limit variables and design the experiments and collect data again. Values of variables are identified from data which shows improvement. This would lead to narrowing down the variables and modify the processes, to achieve improvement continually. The solutions suggested are to be implemented and results are to be recorded. This data is to be measured at varying intervals to see the status of implementation and the progress of improvement is to be monitored till the suggested improvements become normal routine. When results indicate resolution of problem and the rsults are consistent then Team memebres are to be rewarded and recognized to keep up their morale for future projects.

Who Should Pursue SPS

• Statistical Problem Solving can be pursued by a senior leadership group for example group of quality executives meeting weekly to review quality issues, identify opportunities for costs saving and generate ideas for working smarter across the divisions
• Statistical Problem solving can equally be pursued by a staff work group within an institution that possesses a diversity of experience that can gather data on various product features and tabulate them statistically for drawing conclusions
• The staff work group proposes methods for rethinking and reworking models of collaboration and consultation at the facility
• The senior leadership group and staff work group work in partnership with university faculty and staff to identify research communications and solve problems across the organization

Benefits of Statistical Problem Solving

• Long term commitment to organizations and companies to work smarter.
• Reduces costs, enhances services and increases revenues.
• Mitigating the impact of budget reductions while at the same time reducing operational costs.
• Improving operations and processes, resulting in a more efficient, less redundant organization.
• Promotion of entrepreneurship intelligence, risk taking corporations and engagement across interactions with business and community partners.
• A culture change in a way a business or organization collaborates both internally and externally.
• Identification and solving of problems.
• Helps to repetition of problems
• Meets the mandatory requirement for using scientific methods for problem solving
• Savings in revenue by reducing quality costs
• Ultimate improvement in Bottom -Line
• Improvement in teamwork and morale in working
• Improvement in overall problem solving instead of harping on accountability

Business Impact

• Scientific data backed up problem solving techniques puts the business at higher pedestal in the eyes of the customer.
• Eradication of over consulting within businesses and organizations which may become a pitfall especially where it affects speed of information.
• Eradication of blame game

QSE’s Approach to Statistical Problem Solving

By leveraging vast experience, it has, QSE organizes the entire implementation process for Statistical Problem Solving in to Seven simple steps

• Define the Problem
• List Suspect Variables
• Prioritize Selected Variables
• Evaluate Critical Variables
• Optimize Critical Variables
• Monitor and Measure Results
• Reward/Recognize Team Members
• Define the Problem (Vital Few -Trivial Many):

List All the problems which may be hindering Operational Excellence . Place them in a Histogram under as many categories as required.

Select Problems based on a simple principle of Vital Few that is select few problems which contribute to most deficiencies within the facility

QSE advises on how to Use X and R Charts to gather process data.

• List Suspect Variables:

QSE Advises on how to gather data for the suspect variables involving cross functional teams and available past data

• Prioritize Selected Variables Using Cause and Effect Analysis:

QSE helps organizations to come up prioritization of select variables that are creating the problem and the effect that are caused by them. The details of this exercise are to be represented in the Fishbone Diagram or Ishikawa Diagram

• Evaluate Critical Variables:

Use Brain Storming method to use critical variables for collecting process data and Incremental Improvement for each selected critical variable

QSE with its vast experiences guides and conducts brain storming sessions in the facility to identify KAIZEN (Small Incremental projects) to bring in improvements. Create a bench mark to be achieved through the suggested improvement projects

• Optimize Critical Variable Through Implementing the Incremental Improvements:

QSE helps facilities to implement incremental improvements and gather data to see the results of the efforts in improvements

• Monitor and Measure to Collect Data on Consolidated incremental achievements :

Consolidate and make the major change incorporating all incremental improvements and then gather data again to see if the benchmarks have been reached

QSE educates and assists the teams on how these can be done in a scientific manner using lean and six sigma techniques

QSE organizes verification of Data to compare the results from the original results at the start of the projects. Verify if the suggestions incorporated are repeatable for same or better results as planned

              Validate the improvement project by multiple repetitions

• Reward and Recognize Team Members:

QSE will provide all kinds of support in identifying the great contributors to the success of the projects and make recommendation to the Management to recognize the efforts in a manner which befits the organization to keep up the morale of the contributors.

Need Certification?

Quality System Enhancement has been a leader in global certification services for the past 30 years . With more than 800 companies successfully certified, our proprietary 10-Step Approach™ to certification offers an unmatched 100% success rate for our clients.

Recent Posts

Cdfa proposition 12 – farm animal confinement.

ISO 27001 Flyer

ISO 27701 Flyer

Have a question, sign up for our newsletter.

Hear about the latest industry trends from the QSE team of experts. Receive special offers for training services and invitations to free webinars.

ISO Standards

• ISO 9001:2015
• ISO 10993-1:2018
• ISO 13485:2016
• ISO 14001:2015
• ISO 15189:2018
• ISO 15190:2020
• ISO 15378:2017
• ISO/IEC 17020:2012
• ISO/IEC 17025:2017
• ISO 20000-1:2018
• ISO 22000:2018
• ISO 22301:2019
• ISO 27001:2015
• ISO 27701:2019
• ISO 28001:2007
• ISO 37001:2016
• ISO 45001:2018
• ISO 50001:2018
• ISO 55001:2014

Telecommunication Standards

• TL 9000 Version 6.1

Automotive Standards

• IATF 16949:2016
• ISO/SAE 21434:2021

Aerospace Standards

Forestry standards.

• FSC - Forest Stewardship Council
• PEFC - Program for the Endorsement of Forest Certification
• SFI - Sustainable Forest Initiative

Steel Construction Standards

Food safety standards.

• FDA Gluten Free Labeling & Certification
• Hygeine Excellence & Sanitation Excellence

GFSI Recognized Standards

• BRC Version 9
• FSSC 22000:2019
• Hygeine Excellent & Sanitation Excellence
• IFS Version 7
• SQF Edition 9
• All GFSI Recognized Standards for Packaging Industries

Problem Solving Tools

• Corrective & Preventative Actions
• Root Cause Analysis
• Supplier Development

Excellence Tools

• Bottom Line Improvement
• Customer Satisfaction Measurement
• Document Simplification
• Hygiene Excellence & Sanitation
• Lean & Six Sigma
• Malcom Baldridge National Quality Award
• Operational Excellence
• Safety (including STOP and OHSAS 45001)
• Sustainability (Reduce, Reuse, & Recycle)
• Total Productive Maintenance

Other Standards

• California Transparency Act
• Global Organic Textile Standard (GOTS)
• Hemp & Cannabis Management Systems
• Recycling & Re-Using Electronics
• ESG - Environmental, Social & Governance
• CDFA Proposition 12 Animal Welfare

Simplification Delivered™

QSE has helped over 800 companies across North America achieve certification utilizing our unique 10-Step Approach ™ to management system consulting. Schedule a consultation and learn how we can help you achieve your goals as quickly, simply and easily as possible.

Using Statistics to Improve Problem Solving Skills

Problem-solving is an essential skill that everyone must possess, and statistics is a powerful tool that can be used to help solve problems. Statistics uses probability theory as its base and has a rich assortment of submethods, such as probability theory, correlation analysis, estimation theory, sampling theory, hypothesis testing, least squares fitting, chi-square testing, and specific distributions.

Each of these submethods has its unique set of advantages and disadvantages, so it is essential to understand the strengths and weaknesses of each method when attempting to solve a problem.

Introduction

Overview of Problem-Solving

Role of statistics in problem-solving, probability theory, correlation analysis.

Introduction: Problem-solving is a fundamental part of life and an essential skill everyone must possess. It is an integral part of the learning process and is used in various situations. When faced with a problem, it is essential to have the necessary tools and knowledge to identify and solve it. Statistics is one such tool that can be used to help solve problems.

Problem-solving is the process of identifying and finding solutions to a problem. It involves understanding the problem, analyzing the available information, and coming up with a practical and effective solution. Problem-solving is used in various fields, including business, engineering, science, and mathematics.

Statistics is a powerful tool that can be used to help solve problems. Statistics uses probability theory as its base, so when your problem can be stated as a probability, you can reliably go to statistics as an approach. Statistics, as a discipline, has a rich assortment of submethods, such as probability theory, correlation analysis, estimation theory, sampling theory, hypothesis testing, least squares fitting, chi-square testing, and specific distributions (e.g., Poisson, Binomial, etc.).

Probability theory is the mathematical study of chance. It is used to analyze the likelihood of an event occurring. Probability theory is used to determine the likelihood of an event, such as the probability of a coin landing heads up or a certain number being drawn in a lottery. Probability theory is used in various fields, including finance, economics, and engineering.

Correlation analysis is used to determine the relationship between two variables. It is used to identify the strength of the relationship between two variables, such as the correlation between the temperature and the amount of rainfall. Correlation analysis is used in various fields, including economics, finance, and psychology.

Estimation Theory

Estimation theory is used to estimate the value of a variable based on a set of data. It is used to estimate the value of a variable, such as a city's population, based on a sample of the population. Estimation theory is used in various fields, including economics, finance, and engineering.

Conclusion: Statistics is a powerful tool that can be used to help solve problems. Statistics uses probability theory as its base, so when your problem can be stated as a probability, you can reliably go to statistics as an approach. Statistics, as a discipline, has a rich assortment of submethods, such as probability theory, correlation analysis, estimation theory, sampling theory, hypothesis testing, least squares fitting, chi-square testing, and specific distributions (e.g., Poisson, Binomial, etc.). Each submethod has unique advantages and disadvantages, so it is essential to select the one that best suits your problem. With the right approach and tools, statistics can be a powerful tool in problem-solving.

Statistics are the key to unlocking better problem-solving skills - the more you know, the more you can do. IIENSTITU

What role does probability theory play in using statistics to improve problem solving skills?

Probability theory and statistics are both essential tools for problem-solving, and the two disciplines share an interdependent solid relationship. This article will discuss the role that probability theory plays in using statistics to improve problem-solving skills.

Probability theory provides a framework for understanding the behavior of random variables and their associated distributions. We can use statistics to make better predictions and decisions by understanding and applying probability theory. For example, when calculating the probability of a desired outcome, we can use statistical methods to determine the likelihood of that outcome occurring. This can be used to inform decisions and help us optimize our strategies.

Statistics also provide us with powerful tools for understanding the relationship between variables. By analyzing the correlation between two or more variables, we can gain valuable insights into the underlying causes and effects of a problem. For example, by studying a correlation between two variables, we can determine which variable is more likely to cause a particular outcome. This can help us to design more effective solutions to problems.

By combining probability theory and statistics, we can develop powerful strategies for problem-solving. Probability theory helps us understand a problem's underlying structure, while statistics provide us with the tools to analyze the data and make better predictions. By understanding how to use these two disciplines together, we can develop more effective solutions to difficult problems.

In conclusion, probability theory and statistics are both essential for problem-solving. Probability theory provides a framework for understanding the behavior of random variables, while statistics provide powerful tools for understanding the relationships between variables. By combining the two disciplines, we can develop more effective strategies for solving complex problems.

How can correlation analysis be used to identify relationships between variables when solving problems?

Correlation analysis is a powerful tool for identifying relationships between variables when solving problems. It is a statistical approach that measures how two variables are related. By analyzing the correlation between two variables, researchers can identify the strength and direction of their relationship. For example, a correlation analysis can determine if a change in one variable is associated with a change in the other.

When conducting correlation analysis, researchers often use Pearson’s correlation coefficient (r) to measure the strength of the association between two variables. This coefficient ranges from -1 to +1, where -1 indicates a perfect negative correlation, 0 indicates no correlation, and +1 indicates a perfect positive correlation. A perfect positive correlation indicates that when one variable increases, the other variable also increases, and a perfect negative correlation indicates that when one variable increases, the other variable decreases.

Correlation analysis helps identify relationships between variables when solving problems. For example, in a study of the relationship between dietary habits and body weight, a researcher may use correlation analysis to determine if there is a relationship between the two variables. Suppose the researcher finds a significant correlation between dietary habits and body weight. In that case, this can provide insight into the studied problem and help inform solutions.

Correlation analysis can also be used to identify causal relationships between variables. By examining the relationship between two variables over time, researchers can determine if a change in one variable is associated with a change in the other. For example, a researcher may use correlation analysis to determine if temperature changes are associated with changes in air quality. If a significant correlation is found, then the researcher can conclude that temperature changes are likely causing changes in air quality.

Overall, correlation analysis is a powerful tool for identifying relationships between variables when solving problems. By examining the strength and direction of the relationship between two variables, researchers can gain insight into the problem being studied and inform potential solutions.

What are the benefits of using estimation theory when attempting to solve complex problems?

Estimation theory is a powerful tool when attempting to solve complex problems. This theory involves making educated guesses or estimations about the value of a quantity that is difficult or impossible to measure directly. By utilizing estimation theory, one can reduce uncertainty and make decisions more confidently.

The main benefit of using estimation theory is that it allows for the quantification of uncertainty. By estimating, one can determine the range of possible outcomes and make decisions based on the likelihood of each outcome. This helps to reduce the risks associated with making decisions as it allows one to make better decisions based on the available data.

Another benefit of using estimation theory is that it can be applied to many problems. Estimation theory can be used to solve problems in fields such as engineering, finance, and economics. It can also be used to estimate a stock's value, the project's cost, or the probability of a certain event. Estimation theory is also useful in predicting the behavior of a system over time.

Estimation theory can also be used to make decisions in cases where the data is limited. By estimating, one can reduce the amount of data needed to make a decision and make more informed decisions. Furthermore, estimation theory can be used to make decisions even when the data is incomplete or inaccurate. This is especially useful when making decisions in situations where the data is uncertain or incomplete.

In conclusion, estimation theory is a powerful tool for solving complex problems. It can be used to reduce uncertainty, make decisions in cases where data is limited or incomplete, and make predictions about the behavior of a system over time. By utilizing estimation theory, one can make more informed decisions and reduce the risks associated.

How does the application of statistical methods contribute to effective problem-solving in various fields?

**Statistical Methods in Problem-solving** Statistical methods play a crucial role in effective problem-solving across various fields, including natural and social sciences, economics, and engineering. One primary contribution lies in the quantification and analysis of data. **Data Quantification and Analysis** Through descriptive statistics, researchers can summarize, organize, and simplify large data sets, enabling them to extract essential features and identify patterns. In turn, this fosters a deeper understanding of complex issues and aids in data-driven decision-making. **Prediction and Forecasting** Statistical methods can help predict future trends and potential outcomes with a certain level of confidence by extrapolating obtained data. Such prediction models are invaluable in fields as diverse as finance, healthcare, and environmental science, enabling key stakeholders to take proactive measures. **Hypothesis Testing** In the scientific process, hypothesis testing enables practitioners to make inferences about populations based on sample data. By adopting rigorous statistical methods, researchers can determine the likelihood of observed results occurring randomly or due to a specific relationship, thus validating or refuting hypotheses. **Quality Control and Improvement** In industries and manufacturing, statistical methods are applied in quality control measures to ensure that products and services meet established standards consistently. By identifying variations, trends, and deficiencies within production processes, statistical techniques guide improvement efforts. **Design of Experiments** Statistical methods are vital in the design of experiments, ensuring that the collected data is representative, reliable, and unbiased. By utilizing techniques such as random sampling and random assignment, researchers can mitigate confounding variables, increase generalizability, and establish causal relationships. In conclusion, the application of statistical methods contributes to effective problem-solving across various fields by enabling data quantification, analysis, and prediction. Additionally, these methods facilitate hypothesis testing, quality control, and the design of experiments, fostering confidence in decision-making and enhancing outcomes.

In what ways can statistical analysis enhance the decision-making process when facing complex challenges?

Statistical analysis in decision-making Statistical analysis plays a crucial role in the decision-making process when facing complex challenges by enabling evidence-based decisions. It provides a systematic approach to accurately interpret data and transform it into meaningful and actionable insights. In turn, these insights enhance decision-making by reducing uncertainty, minimizing risks, and increasing confidence in the chosen strategy. Quantitative approach By adopting a quantitative approach, decision-makers can objectively evaluate various options using statistical techniques, such as regression analysis or hypothesis testing. This process facilitates the identification of patterns and relationships within the data, highlighting crucial factors that can significantly impact desired outcomes. Consequently, leaders can make informed decisions that optimize available resources and maximize benefits, ultimately increasing the overall success rate of implemented strategies. Addressing biases Statistical analysis helps to address cognitive biases that may otherwise cloud judgment and impede the decision-making process. These biases could include confirmation bias, anchoring bias, and availability heuristic, among others. Employing quantitative methods illuminates the influence these biases may have on subjective interpretations and assists decision-makers in mitigating potential negative impacts. Risk analysis In the context of complex challenges, risk analysis plays an essential role in decision-making. By employing statistical models, decision-makers can quantify risk, estimate probabilities of potential outcomes, and determine the optimal balance between risk and reward. This information can be invaluable for organizations when allocating resources, prioritizing projects, and managing uncertainty in dynamic environments. Data-driven forecasts Statistical analysis enables decision-makers to create accurate forecasts by extrapolating historical data and incorporating current trends. These forecasts can inform strategic planning, budget allocations, and resource management, reducing the likelihood of unforeseen obstacles and ensuring long-term success. In addition to providing a strong basis for future planning, these data-driven predictions also enable organizations to quickly adapt and respond to emerging trends and challenges. In conclusion, statistical analysis is an invaluable tool for enhancing the decision-making process when facing complex challenges. By adopting a quantitative approach, addressing cognitive biases, conducting risk analysis, and producing data-driven forecasts, decision-makers can make informed choices that optimize outcomes and minimize potential risks.

How can concepts like statistical hypothesis testing and regression analysis be applied to solve real-world problems and make informed decisions?

Applications of Hypothesis Testing Statistical hypothesis testing can be a vital tool in decision-making processes, particularly when it comes to addressing real-world problems. In business, for example, managers may use hypothesis testing to determine whether a new product or strategy will lead to higher revenues or customer satisfaction. This can then inform their decisions on whether to invest in the product or strategy or explore other options. In medicine, researchers can use hypothesis testing to compare the effectiveness of a new treatment or intervention compared to standard care, which can provide valuable evidence to guide clinical practice. Regression Analysis to Guide Decisions Similarly, regression analysis is a powerful statistical technique used to understand relationships between variables and predict future outcomes. By modeling the connections between different factors, businesses can make data-driven decisions and develop strategies based on relationships found in historical data. For instance, companies can use regression analysis to forecast future sales, evaluate the return on investment for marketing campaigns, or identify factors that contribute to customer churn. In fields like public health, policymakers can use regression analysis to identify the effects of various interventions on health outcomes, leading to more effective resource allocation and targeting of mass media campaigns. Assessing Real-World Solutions The implementation of statistical hypothesis testing and regression analysis enables stakeholders across diverse disciplines to evaluate and prioritize potential solutions to complex problems. By identifying significant relationships between variables and outcomes, practitioners can develop evidence-based approaches to improve decision-making processes. These methods can be applied to problems in various fields, such as healthcare, public policy, economics, and environmental management, ultimately providing benefits for both individuals and society. Ensuring Informed Decisions In conclusion, both statistical hypothesis testing and regression analysis have a vital role in solving real-world problems and informing decisions. These techniques provide decision-makers with the necessary evidence to evaluate different options, strategies, or interventions to make the most appropriate choices. By incorporating these statistical methods into the decision-making process, stakeholders can increase confidence in their conclusions and improve the overall effectiveness of their actions, leading to better outcomes in various fields.

How does the use of descriptive and inferential statistics improve our understanding of complex problems and inform decision-making?

The Importance of Descriptive and Inferential Statistics in Problem Solving Descriptive statistics provide essential context Descriptive statistics summarize, organize, and simplify data, offering a comprehensive snapshot of a data set. By presenting data in a meaningful and easily interpretable manner, descriptive statistics enable researchers to understand and describe the key characteristics of a data set. This initial step in any data analysis is crucial for establishing context, identifying patterns, and generating hypotheses that contribute to a better understanding of complex problems. Inferential statistics as a tool for decision-making Inferential statistics, on the other hand, involve drawing conclusions and making generalizations about a larger population based on the analysis of a sample. Through hypothesis testing, confidence intervals, and regression analysis, researchers can determine relationships among variables, identify trends, and predict outcomes. By offering insights that go beyond the data at hand, inferential statistics enable researchers to make informed decisions and create strategies for tackling complex problems. The synergy of descriptive and inferential statistics In combination, both descriptive and inferential statistics enhance the understanding and decision-making process in various fields. Descriptive statistics provide a solid foundation by organizing and summarizing data, while inferential statistics enable researchers to delve deeper, uncovering relationships and trends that facilitate evidence-based decision-making. This combination empowers researchers to identify solutions and make more informed decisions when tackling complex problems.

What is the role of experimental design and sampling techniques in ensuring reliable and accurate conclusions when utilizing statistical analysis for problem-solving?

Role of Experimental Design Experimental design plays a pivotal role in ensuring reliable and accurate conclusions in statistical analysis when solving problems. A well-defined experimental design outlines a systematic approach to conducting research, including the selection of participants, allocation of resources, and timing of interventions. It helps control potential confounding factors and biases, allowing researchers to attribute the study results to the intended interventions accurately. Moreover, experimental design enables researchers to quantify uncertainty in their findings through hypothesis testing, thereby establishing the statistical significance of their conclusions. Sampling Techniques Sampling techniques are another essential component in achieving valid and reliable results in statistical analysis. They ensure that the data collected from a population is representative of the whole, thus allowing for accurate generalizations. Proper sampling techniques, such as random sampling or stratified sampling, minimize the prevalence of sampling bias, which may otherwise lead to false or skewed conclusions. Additionally, determining the appropriate sample size—large enough to maintain statistical accuracy and minimize type I and type II errors—is crucial in enhancing the reliability and precision of study results. Achieving Accurate Conclusions To draw accurate conclusions in statistical analysis, researchers must ensure that their experimental design and sampling techniques are carefully planned and executed. This involves selecting the most appropriate methods in accordance with study goals and population demographics. Furthermore, vigilance regarding potential confounders and biases, and continuous monitoring of data quality, contribute to the validity and reliability of statistical findings for problem-solving. Overall, a skillful combination of experimental design and sampling techniques is imperative for researchers to derive reliable and accurate conclusions from statistical analysis. By addressing potential pitfalls and adhering to best practices, this potent mix of methodologies allows for efficient problem-solving and robust insights into diverse research questions.

How do visualization techniques and exploratory data analysis contribute to a more effective interpretation of statistical findings in the context of real-world issues?

Enhancing Interpretation through Visualization Techniques Visualization techniques play a significant role in interpreting statistical findings related to real-world issues. By converting complex data into visually appealing and easy-to-understand formats, these techniques allow decision-makers to quickly grasp the underlying patterns and trends. Graphs, plots, and charts are some common visualization tools that make data more accessible, aiding in the identification of outliers and hidden relationships among variables. Exploratory Data Analysis: A Key Step Exploratory data analysis (EDA) is critical for effective interpretation of statistical findings. This approach involves an initial assessment of the data's characteristics, emphasizing summarizing and visualizing key aspects. Employing EDA allows researchers to identify errors, missing values, and inconsistencies in the data, which is instrumental when addressing real-world issues. By obtaining insights into the dataset's structure and potential biases, analysts can formulate appropriate statistical models and ensure more accurate predictions and inferences. Complementarity for Improved Data Interpretation Combining visualization techniques and EDA contributes to a more effective interpretation of statistical findings by offering a complementary approach. Visualization supports the exploration of data, enabling pattern and relationship identification, while EDA provides a deeper insight into data quality and potential limitations. Together, these methods facilitate a comprehensive understanding of the data, allowing for a more informed decision-making process when addressing real-world issues. In conclusion, visualization techniques and exploratory data analysis are essential tools for effectively interpreting statistical findings. By offering complementary benefits, they enhance decision-making processes and increase the likelihood of informed choices when examining real-world issues. As our world continues to produce vast amounts of data, these methods will remain critical to ensuring that statistical findings are accurate, relevant, and useful in solving pressing problems.

How does statistics help in problem-solving?

Role of Statistics in Problem-solving Understanding the Problem Statistics play a significant role in problem-solving by providing accurate data and quantitative evidence to better understand complex issues. The collection, analysis, and interpretation of numerical data enable decision-makers to observe trends, patterns, and relationships within the data, thus facilitating informed decision-making. To effectively solve problems, it is crucial to have a thorough understanding of the issue at hand, and statistics provide the necessary tools to explore and interpret the relevant data. Identifying Patterns and Trends Statistics help in identifying underlying patterns and trends within a dataset, which aids in understanding the problem's nature and behavior. By employing graphical and numerical techniques, statisticians can visualize relationships, fluctuations, and distributions within the data. Identifying these patterns can lead to the generation of hypotheses, proposing possible solutions, and implementing interventions to address the issues. Evaluating Solutions Once potential solutions are identified, statistics can be used to objectively evaluate their effectiveness by comparing the outcomes of different scenarios or interventions. Experimental designs such as controlled trials, surveys, and longitudinal studies are powerful tools for assessing the impact of problem-solving strategies. Furthermore, statistical significance testing allows decision-makers to determine the likelihood of results occurring by chance, providing more confidence in the selected solutions. Making Informed Decisions Through the use of statistical methods, decision-makers can be guided towards making more informed, evidence-based choices when solving problems. By basing decisions on empirical data, rather than relying on anecdotal evidence, intuition, or assumptions, organizations and policymakers can significantly improve the likelihood of producing successful outcomes. Statistical analysis enables the ranking of possible solutions according to their efficacy, which is crucial for resource allocation and prioritization within any setting. In conclusion, statistics play a crucial role in problem-solving by providing a systematic and rigorous approach to understanding complex issues, identifying patterns and trends, evaluating potential solutions, and guiding informed decision-making. The use of quantitative data and statistical methods allows for greater objectivity, accuracy, and confidence in the process of solving problems and ultimately leads to more effective and efficient solutions.

What are the five statistical processes in solving a problem?

Statistical Processes Overview The process of solving a problem using statistical methods involves five key steps. These steps enable researchers to analyze data and make inferences based on the results. 1. Defining the Problem The first step in any statistical problem-solving process is to clearly define the problem. This involves identifying the research question, objective, or hypothesis that needs to be tested. The problem should be specific and clearly stated to guide the subsequent steps in the process. 2. Data Collection Once the problem is defined, the next step is to collect data that will be used for analysis. Data can be collected through various methods, such as surveys, experiments, or secondary sources. The choice of data collection method should be based on the nature of the problem and the type of data required. It is important to collect data accurately and consistently to ensure the validity of the analysis. 3. Data Organization and Summarization After collecting the data, it needs to be organized and summarized in a way that makes it easy to analyze. This may involve using tables, graphs, or charts to display the data. Descriptive statistics, such as measures of central tendency (mean, median, mode) and measures of dispersion (range, variance, standard deviation), can be used to summarize the data. 4. Analysis and Interpretation At this stage, the data is analyzed using various statistical techniques to answer the research question or test the hypothesis. Inferential statistics, such as correlation analysis or hypothesis testing, can be employed to make inferences about the underlying population based on the sample data. It is crucial to choose the appropriate statistical method for the analysis, keeping in mind the research question and the nature of the data. 5. Drawing Conclusions and Recommendations The final step in the statistical process is to draw conclusions from the analysis and provide recommendations based on the findings. This involves interpreting the results of the analysis in the context of the research question and making generalizations or predictions about the population. The conclusions and recommendations should be communicated effectively, ensuring that they are relevant and useful for decision-making or further research. In conclusion, the five statistical processes in solving a problem are defining the problem, data collection, data organization and summarization, analysis and interpretation, and drawing conclusions and recommendations. These steps allow researchers to effectively analyze data and make informed decisions and predictions based on the results.

How can you use statistics effectively to resolve problems in everyday life?

Understanding the Basics of Statistics Statistics provides a systematic method for individuals to collect, analyze and interpret data. Through this approach, one can efficiently utilize these results to tackle issues they may encounter daily. In the ensuing discussion, we will delve into the process of incorporating statistics to address these everyday concerns effectively. Identifying the Problem Firstly, it is essential to accurately outline the issue at hand. This preliminary stage entails formulating definitive questions, which will guide the data gathering process. Such specificity ensures the assembled information directly pertains to the focal problem and eliminates the possibility of superfluous distractions. Collecting Relevant Data Next, amassing reliable and diverse information allows for well-informed interpretations. To successfully achieve this, it is crucial to identify suitable sources that offer the pertinent data required for a comprehensive analysis. Moreover, obtaining data from diverse sources helps mitigate the potential for biased or skewed outcomes. Implementing Appropriate Statistical Techniques Upon compiling a robust dataset, the implementation of applicable statistical methods becomes crucial. Techniques such as descriptive statistics (e.g., mean, median, mode) or inferential statistics (e.g., regression, ANOVA) empower individuals to systematically extract informative conclusions. Ultimately, this data-driven process leads to a deeper understanding of the issue at hand and facilitates informed decision-making. Interpreting Results and Drawing Conclusions The final step involves rigorously assessing the conclusions derived from statistical analyses. This careful evaluation demands a thorough examination of any potential limitations or biases. Additionally, acknowledging alternative interpretations strengthens the overall argument by mitigating the risk of oversimplifying complex matters. Incorporating Feedback and Adjustments A critical aspect of effectively applying statistics revolves around the willingness to reevaluate one's approach. Engaging in an iterative process and incorporating feedback helps refine the problem-solving strategy, ultimately leading to more accurate and reliable solutions. In summary, the proper use of statistics has the potential to greatly enhance individuals' ability to resolve problems in everyday life. By employing a methodical approach that involves identifying the issue, collecting relevant data, utilizing suitable techniques and critically evaluating conclusions, one can swiftly address concerns and make informed decisions.

How can statistical inference be utilized to draw conclusions about a population when only a sample is available for analysis?

Statistical Inference and Population Analysis Statistical inference is an essential tool in understanding populations. It allows scientists to analyze a small, representative subset or sample of a larger population. This way, we can extract conclusions about an entire population from the analysis of a sample. Use of Sample Analysis In sample analysis, researchers collect data from a smaller subset instead of assessing the entire population. It significantly reduces the required resources and time. Nevertheless, a sample must adequately represent the characteristics of the population for valid inferences. Role of Probability Probability plays a pivotal role in statistical inference. The application of probability theories provides information about the likelihood of particular results. The conclusions drawn about the population feature a degree of certainty conveyed by probability. Statistical Tests Stepping further, statistical tests employed in the process illuminate the differences between groups within the sample. They provide guidelines for finding if observed differences occurred due to chance. By employing these tests, we can generalize findings from a sample to the entire population. Importance of Confidence Intervals Confidence intervals are another critical component of statistical inference. They present the range of values within which we expect the population value to fall a certain percent of the time, say 95%. Confidence intervals reveal more about the population parameter than a single point estimate. Conclusion and Future Predictions Between sample analysis, probability, statistical tests, and confidence intervals, statistical inference enables efficient, accurate conclusions about large population groups. Its effective use facilitates not only a comprehensive understanding of the present population status but also assists in predicting future trends. In a nutshell, statistical inference acts as a bridge connecting sample data to meaningful conclusions about the broader population. By analyzing a sample, predicting probabilities, applying statistical tests, and measuring confidence intervals, we can glean holistic insights about the entire population.

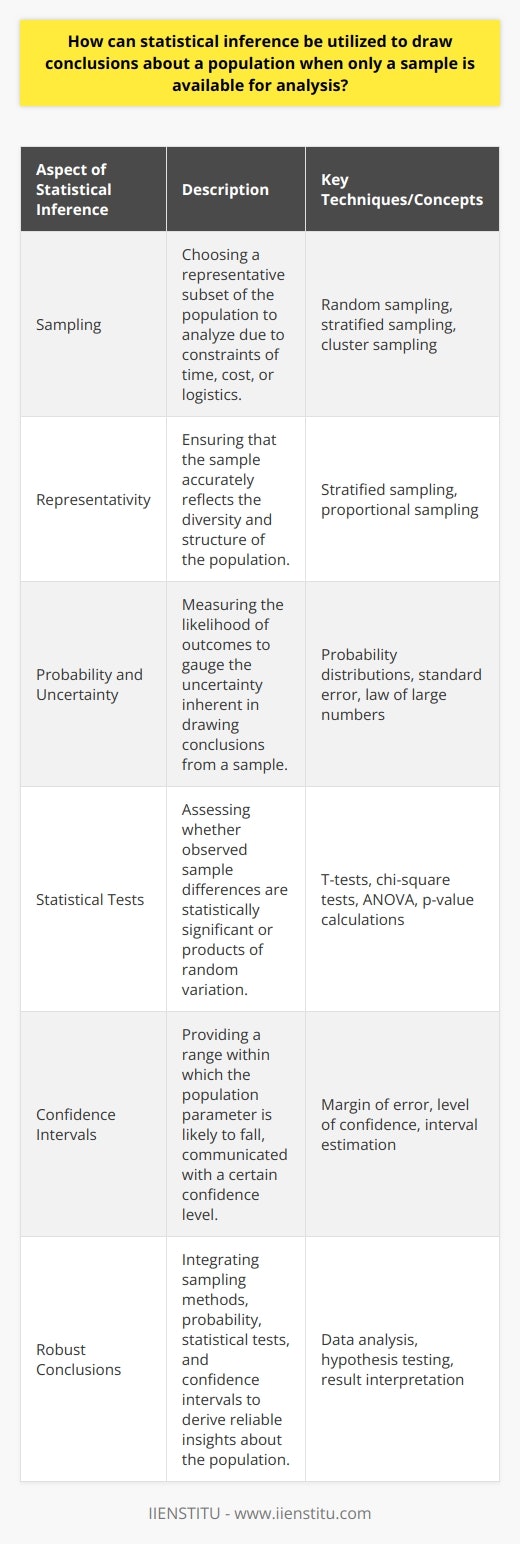
What are the key principles of robust statistical modeling, and how can these principles be applied to enhance the effectiveness of problem-solving efforts?

Understanding Robust Statistical Modeling Principles Robust statistical modeling works on three key principles. They are the use of robust measures, an effective model selection strategy, and consideration of outliers. These principles play a crucial role to ensure the robustness of statistical results. Applying Robust Measures The first principle revolves around applying robust measures. These measures are resistant to the outliers in the data set. They work by minimizing the effect of extreme values. By using these robust measures, researchers can increase the accuracy of their statistical models. Model Selection Strategy Next comes the strategy for selecting the model. It involves choosing an appropriate statistical model that aligns well with the provided data set. In this case, the most reliable models are ones that demonstrate significant results and fit the data well. Selecting an efficient model, hence, can lead to more accurate predictions or inferences. Addressing Outliers Finally, a detailed consideration of outliers is vital. Outliers can skew the results of a model significantly. They need careful handling to prevent any bias in the final results. Recognizing and appropriately managing these outliers aids in maintaining the integrity of statistical findings. Enhancing Problem-Solving Efforts These principles, when applied effectively, can significantly enhance problem-solving efforts. By using robust measures, researchers can achieve more accurate results, increasing the credibility of their findings. A well-chosen model can enhance the interpretability and usefulness of the results. Furthermore, careful handling of outliers can prevent skewed results, ensuring more reliable conclusions. In essence, by embracing these principles, one can substantially elevate their problem-solving capabilities, making the process more efficient and effective. Thus, robust statistical modeling acts as a powerful tool in addressing various research questions and solving complex problems.

How can the utilizations of time series analysis in statistics support trend identification and forecasting in the context of complex/problem-solving situations?

Identifying Trends with Time Series Analysis: A crucial aspect of time series analysis in statistics is trend identification. Time series analysis allows statisticians to discern patterns in data collected over time. These trends indicate changes in variables, creating a historical line that tracks these alterations across a span of time. Support for Complex Problem Solving: In complex problem-solving situations, time series analysis can provide valuable support. Specifically, it can facilitate independent, variable-dependent trend analysis and insights into relationships within data sequences. This is vital for complex situations requiring deeper analysis. Time Series Analysis for Forecasting: Another primary use of time series analysis is for forecast predictions in future scenarios. By analyzing the trends identified, predictions can suggest plausible future scenarios. This forecasting capability can be critical in planning and preparation for potential future events based on the observed trends. Predictive Modeling: Predictive modeling can be improved with time series analysis. It helps understand population trends or related metrics. By revealing underlying patterns, time series analysis supports data-driven decision making in complex situations. In summary, time series analysis plays an instrumental role in statistics. Through trend identification and forecasting, it provides invaluable support for complex problem-solving situations. This statistical tool is essential for those working in an environment that requires a clear, predictive understanding of data over time.

How can statistics help with problem solving?

Effective Use of Statistics Statistics offers efficient problem-solving tools. They provide the ability to measure, forecast, and make informed decisions. When faced with a problem, statistics help in gathering relevant data. Understanding the Problem Statistics helps to describe the problem objectively. Before proceeding with problem solving, a clear definition of the problem is necessary. Statistics describe problems quantitatively, bringing precision in problem definition. Identifying Solutions Statistics aids in identifying potential solutions. By using predictive analytics, statistics can forecast the outcomes of various solutions. Thus, it assists in the selection of most efficient solution based on the forecasted results. Evaluating Results Once a solution is implemented, statistics help in evaluation. They measure the effectiveness of the solution by comparing the outcomes with the predicted results. Promoting Continuous Improvement Statistics guide continuous improvement. They pinpoint deviations, enabling identification of areas of improvement. This leads to enhanced effectiveness in problem solving. Statistics has a pivotal role in problem solving. The data-driven approach enhances the credibility of the problem-solving process and the ultimate solutions. The various statistical tools improve both the efficiency and effectiveness, leading to better solutions.

Why is data analysis important in problem solving?

Data Analysis and Problem-Solving: A Crucial Connection Data analysis stands as a critical tool in problem solving in the contemporary business environment. Essentially, it offers insightful measurements of challenges. By examining data, we uncover patterns and trends to identify problems. Identification of Issues The initial step in problem-solving involves the recognition of a problem. It is here that data analysis proves vital. It grants a robust basis for this recognition, presenting objective rather than subjective identifiers. Understanding the Nature of Problems Once we identify a problem, we must understand its nature. In-depth data analysis can provide a detailed insight into why problems arise. It examines multiple variable relationships, often revealing root causes. Generating Solutions Data analysis aids in creating suitable solutions. By understanding the problem from a data perspective, we can draw up potential fixes. These solutions are often grounded on empirical evidence, hence sound and reliable. Evaluating Outcomes After solution implementation, evaluation follows closely. Analyzing data post-implementation helps measure the effectiveness of the solution. It provides a measure on the success of the problem-solving process. In conclusion, data analysis is a strong ally in problem-solving. It facilitates issue identification, enhances understanding, helps to generate solutions, and evaluates outcomes. By utilizing this tool, we can significantly improve our problem-solving efforts, leading to more effective and measurable results.

How does statistics make you a better thinker?

Enhancing Reasoning and Decision Making Skills Statistics equips one with necessary tools to question and interpret data intelligently. It sharpens critical reasoning abilities by offering ways to identify patterns or anomalies, thus improving decision-making efficiency. Understanding Probabilities and Predictions Statistics introduces individuals to the concept of probability, enabling them to weigh the likelihood of different scenarios accurately. Consequently, it allows them to make precise and informed predictions, honing their thinking and analytical skills. Building Quantitative Literacy Statistics promotes quantitative literacy, a vital skill in a data-driven world. Understanding numerical information helps individuals decipher complex data and convert it into actionable insights. This heightens critical thinking abilities and enables better understanding of the world. Critiquing Data Effectively Statistics improves a person's ability to critically analyze presented data. Using statistical tools, one can identify manipulation or misinterpretation in data, preventing them from taking misleading information at face value. Developing Logical Reasoning Statistics fosters effective problem-solving skills by inciting logical reasoning. It drives individuals to meticulously analyze data, look for patterns and draw logical conclusions, thus streamlining strategic decision-making processes. In conclusion, mastering the use of statistics can effectively enhance a person's thinking capacity. It works on multiple fronts ranging from decision-making to quantitative literacy to critiquing data, making one a more discerning and astute individual. Statistics, therefore, plays a pivotal role in developing vital cognitive abilities.

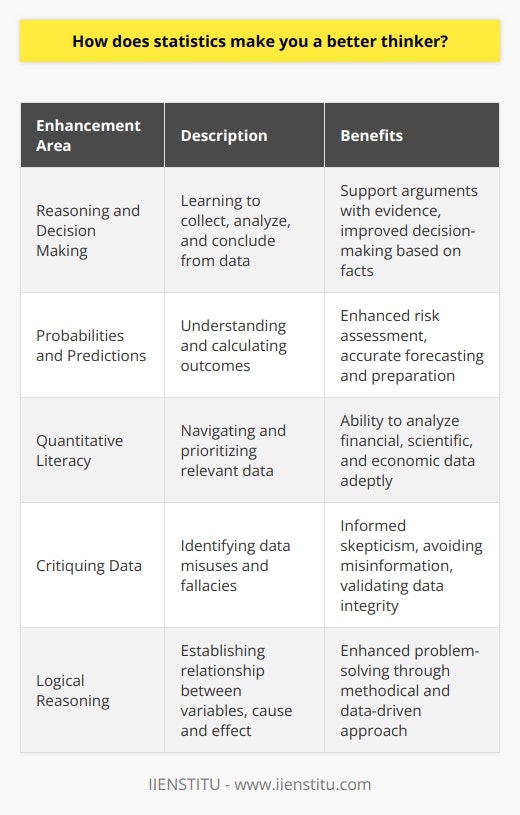
Yu Payne is an American professional who believes in personal growth. After studying The Art & Science of Transformational from Erickson College, she continuously seeks out new trainings to improve herself. She has been producing content for the IIENSTITU Blog since 2021. Her work has been featured on various platforms, including but not limited to: ThriveGlobal, TinyBuddha, and Addicted2Success. Yu aspires to help others reach their full potential and live their best lives.

What are Problem Solving Skills?

3 Apps To Help Improve Problem Solving Skills

How To Improve Your Problem-Solving Skills

How To Become a Great Problem Solver?

An official website of the United States government

The .gov means it’s official. Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you’re on a federal government site.

The site is secure. The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.

• Publications
• Account settings

Preview improvements coming to the PMC website in October 2024. Learn More or Try it out now .

• Advanced Search
• Journal List
• Front Psychol

Statistical Analysis of Complex Problem-Solving Process Data: An Event History Analysis Approach

Yunxiao chen.

1 Department of Statistics, London School of Economics and Political Science, London, United Kingdom

2 School of Statistics, University of Minnesota, Minneapolis, MN, United States

Jingchen Liu

3 Department of Statistics, Columbia University, New York, NY, United States

Zhiliang Ying

Complex problem-solving (CPS) ability has been recognized as a central 21st century skill. Individuals' processes of solving crucial complex problems may contain substantial information about their CPS ability. In this paper, we consider the prediction of duration and final outcome (i.e., success/failure) of solving a complex problem during task completion process, by making use of process data recorded in computer log files. Solving this problem may help answer questions like “how much information about an individual's CPS ability is contained in the process data?,” “what CPS patterns will yield a higher chance of success?,” and “what CPS patterns predict the remaining time for task completion?” We propose an event history analysis model for this prediction problem. The trained prediction model may provide us a better understanding of individuals' problem-solving patterns, which may eventually lead to a good design of automated interventions (e.g., providing hints) for the training of CPS ability. A real data example from the 2012 Programme for International Student Assessment (PISA) is provided for illustration.

1. Introduction

Complex problem-solving (CPS) ability has been recognized as a central 21st century skill of high importance for several outcomes including academic achievement (Wüstenberg et al., 2012 ) and workplace performance (Danner et al., 2011 ). It encompasses a set of higher-order thinking skills that require strategic planning, carrying out multi-step sequences of actions, reacting to a dynamically changing system, testing hypotheses, and, if necessary, adaptively coming up with new hypotheses. Thus, there is almost no doubt that an individual's problem-solving process data contain substantial amount of information about his/her CPS ability and thus are worth analyzing. Meaningful information extracted from CPS process data may lead to better understanding, measurement, and even training of individuals' CPS ability.

Problem-solving process data typically have a more complex structure than that of panel data which are traditionally more commonly encountered in statistics. Specifically, individuals may take different strategies toward solving the same problem. Even for individuals who take the same strategy, their actions and time-stamps of the actions may be very different. Due to such heterogeneity and complexity, classical regression and multivariate data analysis methods cannot be straightforwardly applied to CPS process data.

Possibly due to the lack of suitable analytic tools, research on CPS process data is limited. Among the existing works, none took a prediction perspective. Specifically, Greiff et al. ( 2015 ) presented a case study, showcasing the strong association between a specific strategic behavior (identified by expert knowledge) in a CPS task from the 2012 Programme for International Student Assessment (PISA) and performance both in this specific task and in the overall PISA problem-solving score. He and von Davier ( 2015 , 2016 ) proposed an N-gram method from natural language processing for analyzing problem-solving items in technology-rich environments, focusing on identifying feature sequences that are important to task completion. Vista et al. ( 2017 ) developed methods for the visualization and exploratory analysis of students' behavioral pathways, aiming to detect action sequences that are potentially relevant for establishing particular paths as meaningful markers of complex behaviors. Halpin and De Boeck ( 2013 ) and Halpin et al. ( 2017 ) adopted a Hawkes process approach to analyzing collaborative problem-solving items, focusing on the psychological measurement of collaboration. Xu et al. ( 2018 ) proposed a latent class model that analyzes CPS patterns by classifying individuals into latent classes based on their problem-solving processes.

In this paper, we propose to analyze CPS process data from a prediction perspective. As suggested in Yarkoni and Westfall ( 2017 ), an increased focus on prediction can ultimately lead us to greater understanding of human behavior. Specifically, we consider the simultaneous prediction of the duration and the final outcome (i.e., success/failure) of solving a complex problem based on CPS process data. Instead of a single prediction, we hope to predict at any time during the problem-solving process. Such a data-driven prediction model may bring us insights about individuals' CPS behavioral patterns. First, features that contribute most to the prediction may correspond to important strategic behaviors that are key to succeeding in a task. In this sense, the proposed method can be used as an exploratory data analysis tool for extracting important features from process data. Second, the prediction accuracy may also serve as a measure of the strength of the signal contained in process data that reflects one's CPS ability, which reflects the reliability of CPS tasks from a prediction perspective. Third, for low stake assessments, the predicted chance of success may be used to give partial credits when scoring task takers. Fourth, speed is another important dimension of complex problem solving that is closely associated with the final outcome of task completion (MacKay, 1982 ). The prediction of the duration throughout the problem-solving process may provide us insights on the relationship between the CPS behavioral patterns and the CPS speed. Finally, the prediction model also enables us to design suitable interventions during their problem-solving processes. For example, a hint may be provided when a student is predicted having a high chance to fail after sufficient efforts.

More precisely, we model the conditional distribution of duration time and final outcome given the event history up to any time point. This model can be viewed as a special event history analysis model, a general statistical framework for analyzing the expected duration of time until one or more events happen (see e.g., Allison, 2014 ). The proposed model can be regarded as an extension to the classical regression approach. The major difference is that the current model is specified over a continuous-time domain. It consists of a family of conditional models indexed by time, while the classical regression approach does not deal with continuous-time information. As a result, the proposed model supports prediction at any time during one's problem-solving process, while the classical regression approach does not. The proposed model is also related to, but substantially different from response time models (e.g., van der Linden, 2007 ) which have received much attention in psychometrics in recent years. Specifically, response time models model the joint distribution of response time and responses to test items, while the proposed model focuses on the conditional distribution of CPS duration and final outcome given the event history.

Although the proposed method learns regression-type models from data, it is worth emphasizing that we do not try to make statistical inference, such as testing whether a specific regression coefficient is significantly different from zero. Rather, the selection and interpretation of the model are mainly justified from a prediction perspective. This is because statistical inference tends to draw strong conclusions based on strong assumptions on the data generation mechanism. Due to the complexity of CPS process data, a statistical model may be severely misspecified, making valid statistical inference a big challenge. On the other hand, the prediction framework requires less assumptions and thus is more suitable for exploratory analysis. More precisely, the prediction framework admits the discrepancy between the underlying complex data generation mechanism and the prediction model (Yarkoni and Westfall, 2017 ). A prediction model aims at achieving a balance between the bias due to this discrepancy and the variance due to a limited sample size. As a price, findings from the predictive framework are preliminary and only suggest hypotheses for future confirmatory studies.

The rest of the paper is organized as follows. In Section 2, we describe the structure of complex problem-solving process data and then motivate our research questions, using a CPS item from PISA 2012 as an example. In Section 3, we formulate the research questions under a statistical framework, propose a model, and then provide details of estimation and prediction. The introduced model is illustrated through an application to an example item from PISA 2012 in Section 4. We discuss limitations and future directions in Section 5.

2. Complex Problem-Solving Process Data

2.1. a motivating example.

We use a specific CPS item, CLIMATE CONTROL (CC) 1 , to demonstrate the data structure and to motivate our research questions. It is part of a CPS unit in PISA 2012 that was designed under the “MicroDYN” framework (Greiff et al., 2012 ; Wüstenberg et al., 2012 ), a framework for the development of small dynamic systems of causal relationships for assessing CPS.

In this item, students are instructed to manipulate the panel (i.e., to move the top, central, and bottom control sliders; left side of Figure 1A ) and to answer how the input variables (control sliders) are related to the output variables (temperature and humidity). Specifically, the initial position of each control slider is indicated by a triangle “▴.” The students can change the top, central and bottom controls on the left of Figure 1 by using the sliders. By clicking “APPLY,” they will see the corresponding changes in temperature and humidity. After exploration, the students are asked to draw lines in a diagram ( Figure 1B ) to answer what each slider controls. The item is considered correctly answered if the diagram is correctly completed. The problem-solving process for this item is that the students must experiment to determine which controls have an impact on temperature and which on humidity, and then represent the causal relations by drawing arrows between the three inputs (top, central, and bottom control sliders) and the two outputs (temperature and humidity).

(A) Simulation environment of CC item. (B) Answer diagram of CC item.

PISA 2012 collected students' problem-solving process data in computer log files, in the form of a sequence of time-stamped events. We illustrate the structure of data in Table 1 and Figure 2 , where Table 1 tabulates a sequence of time-stamped events from a student and Figure 2 visualizes the corresponding event time points on a time line. According to the data, 14 events were recorded between time 0 (start) and 61.5 s (success). The first event happened at 29.5 s that was clicking “APPLY” after the top, central, and bottom controls were set at 2, 0, and 0, respectively. A sequence of actions followed the first event and finally at 58, 59.1, and 59.6 s, a final answer was correctly given using the diagram. It is worth clarifying that this log file does not collect all the interactions between a student and the simulated system. That is, the status of the control sliders is only recorded in the log file, when the “APPLY” button is clicked.

An example of computer log file data from CC item in PISA 2012.

Visualization of the structure of process data from CC item in PISA 2012.

The process data for solving a CPS item typically have two components, knowledge acquisition and knowledge application, respectively. This CC item mainly focuses the former, which includes learning the causal relationships between the inputs and the outputs and representing such relationships by drawing the diagram. Since data on representing the causal relationship is relatively straightforward, in the rest of the paper, we focus on the process data related to knowledge acquisition and only refer a student's problem-solving process to his/her process of exploring the air conditioner, excluding the actions involving the answer diagram.

Intuitively, students' problem-solving processes contain information about their complex problem-solving ability, whether in the context of the CC item or in a more general sense of dealing with complex tasks in practice. However, it remains a challenge to extract meaningful information from their process data, due to the complex data structure. In particular, the occurrences of events are heterogeneous (i.e., different people can have very different event histories) and unstructured (i.e., there is little restriction on the order and time of the occurrences). Different students tend to have different problem-solving trajectories, with different actions taken at different time points. Consequently, time series models, which are standard statistical tools for analyzing dynamic systems, are not suitable here.

2.2. Research Questions

We focus on two specific research questions. Consider an individual solving a complex problem. Given that the individual has spent t units of time and has not yet completed the task, we would like to ask the following two questions based on the information at time t : How much additional time does the individual need? And will the individual succeed or fail upon the time of task completion?

Suppose we index the individual by i and let T i be the total time of task completion and Y i be the final outcome. Moreover, we denote H i ( t ) = ( h i 1 ( t ) , ... , h i p ( t ) ) ⊤ as a p -vector function of time t , summarizing the event history of individual i from the beginning of task to time t . Each component of H i ( t ) is a feature constructed from the event history up to time t . Taking the above CC item as an example, components of H i ( t ) may be, the number of actions a student has taken, whether all three control sliders have been explored, the frequency of using the reset button, etc., up to time t . We refer to H i ( t ) as the event history process of individual i . The dimension p may be high, depending on the complexity of the log file.

With the above notation, the two questions become to simultaneously predict T i and Y i based on H i ( t ). Throughout this paper, we focus on the analysis of data from a single CPS item. Extensions of the current framework to multiple-item analysis are discussed in Section 5.

3. Proposed Method

3.1. a regression model.

We now propose a regression model to answer the two questions raised in Section 2.2. We specify the marginal conditional models of Y i and T i given H i ( t ) and T i > t , respectively. Specifically, we assume

where Φ is the cumulative distribution function of a standard normal distribution. That is, Y i is assumed to marginally follow a probit regression model. In addition, only the conditional mean and variance are assumed for log( T i − t ). Our model parameters include the regression coefficients B = ( b jk )2 × p and conditional variance σ 2 . Based on the above model specification, a pseudo-likelihood function will be devived in Section 3.3 for parameter estimation.

Although only marginal models are specified, we point out that the model specifications (1) through (3) impose quite strong assumptions. As a result, the model may not most closely approximate the data-generating process and thus a bias is likely to exist. On the other hand, however, it is a working model that leads to reasonable prediction and can be used as a benchmark model for this prediction problem in future investigations.

We further remark that the conditional variance of log( T i − t ) is time-invariant under the current specification, which can be further relaxed to be time-dependent. In addition, the regression model for response time is closely related to the log-normal model for response time analysis in psychometrics (e.g., van der Linden, 2007 ). The major difference is that the proposed model is not a measurement model disentangling item and person effects on T i and Y i .

3.2. Prediction

Under the model in Section 3.1, given the event history, we predict the final outcome based on the success probability Φ( b 11 h i 1 ( t ) + ⋯ + b 1 p h ip ( t )). In addition, based on the conditional mean of log( T i − t ), we predict the total time at time t by t + exp( b 21 h i 1 ( t ) + ⋯ + b 2 p h ip ( t )). Given estimates of B from training data, we can predict the problem-solving duration and final outcome at any t for an individual in the testing sample, throughout his/her entire problem-solving process.

3.3. Parameter Estimation

It remains to estimate the model parameters based on a training dataset. Let our data be (τ i , y i ) and { H i ( t ): t ≥ 0}, i = 1, …, N , where τ i and y i are realizations of T i and Y i , and { H i ( t ): t ≥ 0} is the entire event history.

We develop estimating equations based on a pseudo likelihood function. Specifically, the conditional distribution of Y i given H i ( t ) and T i > t can be written as

where b 2 = ( b 11 , ... , b 1 p ) ⊤ . In addition, using the log-normal model as a working model for T i − t , the corresponding conditional distribution of T i can be written as

where b 2 = ( b 21 , ... , b 2 p ) ⊤ . The pseudo-likelihood is then written as

where t 1 , …, t J are J pre-specified grid points that spread out over the entire time spectrum. The choice of the grid points will be discussed in the sequel. By specifying the pseudo-likelihood based on the sequence of time points, the prediction at different time is taken into accounting in the estimation. We estimate the model parameters by maximizing the pseudo-likelihood function L ( B , σ).

In fact, (5) can be factorized into

Therefore, b 1 is estimated by maximizing L 1 ( b 1 ), which takes the form of a likelihood function for probit regression. Similarly, b 2 and σ are estimated by maximizing L 2 ( b 2 , σ), which is equivalent to solving the following estimation equations,

The estimating equations (8) and (9) can also be derived directly based on the conditional mean and variance specification of log( T i − t ). Solving these equations is equivalent to solving a linear regression problem, and thus is computationally easy.

3.4. Some Remarks

We provide a few remarks. First, choosing suitable features into H i ( t ) is important. The inclusion of suitable features not only improves the prediction accuracy, but also facilitates the exploratory analysis and interpretation of how behavioral patterns affect CPS result. If substantive knowledge about a CPS task is available from cognition theory, one may choose features that indicate different strategies toward solving the task. Otherwise, a data-driven approach may be taken. That is, one may select a model from a candidate list based on certain cross-validation criteria, where, if possible, all reasonable features should be consider as candidates. Even when a set of features has been suggested by cognition theory, one can still take the data-driven approach to find additional features, which may lead to new findings.

Second, one possible extension of the proposed model is to allow the regression coefficients to be a function of time t , whereas they are independent of time under the current model. In that case, the regression coefficients become functions of time, b jk ( t ). The current model can be regarded as a special case of this more general model. In particular, if b jk ( t ) has high variation along time in the best predictive model, then simply applying the current model may yield a high bias. Specifically, in the current estimation procedure, a larger grid point tends to have a smaller sample size and thus contributes less to the pseudo-likelihood function. As a result, a larger bias may occur in the prediction at a larger time point. However, the estimation of the time-dependent coefficient is non-trivial. In particular, constraints should be imposed on the functional form of b jk ( t ) to ensure a certain level of smoothness over time. As a result, b jk ( t ) can be accurately estimated using information from a finite number of time points. Otherwise, without any smoothness assumptions, to predict at any time during one's problem-solving process, there are an infinite number of parameters to estimate. Moreover, when a regression coefficient is time-dependent, its interpretation becomes more difficult, especially if the sign changes over time.

Third, we remark on the selection of grid points in the estimation procedure. Our model is specified in a continuous time domain that supports prediction at any time point in a continuum during an individual's problem-solving process. The use of discretized grid points is a way to approximate the continuous-time system, so that estimation equations can be written down. In practice, we suggest to place the grid points based on the quantiles of the empirical distribution of duration based on the training set. See the analysis in Section 4 for an illustration. The number of grid points may be further selected by cross validation. We also point out that prediction can be made at any time point on the continuum, not limited to the grid points for parameter estimation.

4. An Example from PISA 2012

4.1. background.

In what follows, we illustrate the proposed method via an application to the above CC item 2 . This item was also analyzed in Greiff et al. ( 2015 ) and Xu et al. ( 2018 ). The dataset was cleaned from the entire released dataset of PISA 2012. It contains 16,872 15-year-old students' problem-solving processes, where the students were from 42 countries and economies. Among these students, 54.5% answered correctly. On average, each student took 129.9 s and 17 actions solving the problem. Histograms of the students' problem-solving duration and number of actions are presented in Figure 3 .

(A) Histogram of problem-solving duration of the CC item. (B) Histogram of the number of actions for solving the CC item.

4.2. Analyses

The entire dataset was randomly split into training and testing sets, where the training set contains data from 13,498 students and the testing set contains data from 3,374 students. A predictive model was built solely based on the training set and then its performance was evaluated based on the testing set. We used J = 9 grid points for the parameter estimation, with t 1 through t 9 specified to be 64, 81, 94, 106, 118, 132, 149, 170, and 208 s, respectively, which are the 10% through 90% quantiles of the empirical distribution of duration. As discussed earlier, the number of grid points and their locations may be further engineered by cross validation.

4.2.1. Model Selection

We first build a model based on the training data, using a data-driven stepwise forward selection procedure. In each step, we add one feature into H i ( t ) that leads to maximum increase in a cross-validated log-pseudo-likelihood, which is calculated based on a five-fold cross validation. We stop adding features into H i ( t ) when the cross-validated log-pseudo-likelihood stops increasing. The order in which the features are added may serve as a measure of their contribution to predicting the CPS duration and final outcome.

The candidate features being considered for model selection are listed in Table 2 . These candidate features were chosen to reflect students' CPS behavioral patterns from different aspects. In what follows, we discuss some of them. For example, the feature I i ( t ) indicates whether or not all three control sliders have been explored by simple actions (i.e., moving one control slider at a time) up to time t . That is, I i ( t ) = 1 means that the vary-one-thing-at-a-time (VOTAT) strategy (Greiff et al., 2015 ) has been taken. According to the design of the CC item, the VOTAT strategy is expected to be a strong predictor of task success. In addition, the feature N i ( t )/ t records a student's average number of actions per unit time. It may serve as a measure of the student's speed of taking actions. In experimental psychology, response time or equivalently speed has been a central source for inferences about the organization and structure of cognitive processes (e.g., Luce, 1986 ), and in educational psychology, joint analysis of speed and accuracy of item response has also received much attention in recent years (e.g., van der Linden, 2007 ; Klein Entink et al., 2009 ). However, little is known about the role of speed in CPS tasks. The current analysis may provide some initial result on the relation between a student's speed and his/her CPS performance. Moreover, the features defined by the repeating of previously taken actions may reflect students' need of verifying the derived hypothesis on the relation based on the previous action or may be related to students' attention if the same actions are repeated many times. We also include 1, t, t 2 , and t 3 in H i ( t ) as the initial set of features to capture the time effect. For simplicity, country information is not taken into account in the current analysis.

The list of candidate features to be incorporated into the model.

Our results on model selection are summarized in Figure 4 and Table 3 . The pseudo-likelihood stopped increasing after 11 steps, resulting a final model with 15 components in H i ( t ). As we can see from Figure 4 , the increase in the cross-validated log-pseudo-likelihood is mainly contributed by the inclusion of features in the first six steps, after which the increment is quite marginal. As we can see, the first, second, and sixth features entering into the model are all related to taking simple actions, a strategy known to be important to this task (e.g., Greiff et al., 2015 ). In particular, the first feature being selected is I i ( t ), which confirms the strong effect of the VOTAT strategy. In addition, the third and fourth features are both based on N i ( t ), the number of actions taken before time t . Roughly, the feature 1 { N i ( t )>0} reflects the initial planning behavior (Eichmann et al., 2019 ). Thus, this feature tends to measure students' speed of reading the instruction of the item. As discussed earlier, the feature N i ( t )/ t measures students' speed of taking actions. Finally, the fifth feature is related to the use of the RESET button.

The increase in the cross-validated log-pseudo-likelihood based on a stepwise forward selection procedure. (A–C) plot the cross-validated log-pseudo-likelihood, corresponding to L ( B , σ), L 1 ( b 1 ), L 2 ( b 2 , σ), respectively.

Results on model selection based on a stepwise forward selection procedure.

The columns “Lik,” “Lik.out,” and “Lik.dur” give the value of the cross-validated log-pseudo-likelihood, corresponding to L(B, σ), L 1 ( b 1 ), L 2 ( b 2 , σ), respectively .

4.2.2. Prediction Performance on Testing Set

We now look at the prediction performance of the above model on the testing set. The prediction performance was evaluated at a larger set of time points from 19 to 281 s. Instead of reporting based on the pseudo-likelihood function, we adopted two measures that are more straightforward. Specifically, we measured the prediction of final outcome by the Area Under the Curve (AUC) of the predicted Receiver Operating Characteristic (ROC) curve. The value of AUC is between 0 and 1. A larger AUC value indicates better prediction of the binary final outcome, with AUC = 1 indicating perfect prediction. In addition, at each time point t , we measured the prediction of duration based on the root mean squared error (RMSE), defined as

where τ i , i = N + 1, …, N + n , denotes the duration of students in the testing set, and τ ^ i ( t ) denotes the prediction based on information up to time t according to the trained model.

Results are presented in Figure 5 , where the testing AUC and RMSE for the final outcome and duration are presented. In particular, results based on the model selected by cross validation ( p = 15) and the initial model ( p = 4, containing the initial covariates 1, t , t 2 , and t 3 ) are compared. First, based on the selected model, the AUC is never above 0.8 and the RMSE is between 53 and 64 s, indicating a low signal-to-noise ratio. Second, the students' event history does improve the prediction of final outcome and duration upon the initial model. Specifically, since the initial model does not take into account the event history, it predicts the students with duration longer than t to have the same success probability. Consequently, the test AUC is 0.5 at each value of t , which is always worse than the performance of the selected model. Moreover, the selected model always outperforms the initial model in terms of the prediction of duration. Third, the AUC for the prediction of the final outcome is low when t is small. It keeps increasing as time goes on and fluctuates around 0.72 after about 120 s.

A comparison of prediction accuracy between the model selected by cross validation and a baseline model without using individual specific event history.

4.2.3. Interpretation of Parameter Estimates

To gain more insights into how the event history affects the final outcome and duration, we further look at the results of parameter estimation. We focus on a model whose event history H i ( t ) includes the initial features and the top six features selected by cross validation. This model has similar prediction accuracy as the selected model according to the cross-validation result in Figure 4 , but contains less features in the event history and thus is easier to interpret. Moreover, the parameter estimates under this model are close to those under the cross-validation selected model, and the signs of the regression coefficients remain the same.

The estimated regression coefficients are presented in Table 4 . First, the first selected feature I i ( t ), which indicates whether all three control sliders have been explored via simple actions, has a positive regression coefficient on final outcome and a negative coefficient on duration. It means that, controlling the rest of the parameters, a student who has taken the VOTAT strategy tends to be more likely to give a correct answer and to complete in a shorter period of time. This confirms the strong effect of VOTAT strategy in solving the current task.

Estimated regression coefficients for a model for which the event history process contains the initial features based on polynomials of t and the top six features selected by cross validation.

Second, besides I i ( t ), there are two features related to taking simple actions, 1 { S i ( t )>0} and S i ( t )/ t , which are the indicator of taking at least one simple action and the frequency of taking simple actions. Both features have positive regression coefficients on the final outcome, implying larger values of both features lead to a higher success rate. In addition, 1 { S i ( t )>0} has a negative coefficient on duration and S i ( t )/ t has a positive one. Under this estimated model, the overall simple action effect on duration is b ^ 25 I i ( t ) + b ^ 26 1 { S i ( t ) > 0 } + b ^ 2 , 10 S i ( t ) / t , which is negative for most students. It implies that, overall, taking simple actions leads to a shorter predicted duration. However, once all three types of simple actions have been taken, a higher frequency of taking simple actions leads to a weaker but sill negative simple action effect on the duration.

Third, as discussed earlier, 1 { N i ( t )>0} tends to measure the student's speed of reading the instruction of the task and N i ( t )/ t can be regarded as a measure of students' speed of taking actions. According to the estimated regression coefficients, the data suggest that a student who reads and acts faster tends to complete the task in a shorter period of time with a lower accuracy. Similar results have been seen in the literature of response time analysis in educational psychology (e.g., Klein Entink et al., 2009 ; Fox and Marianti, 2016 ; Zhan et al., 2018 ), where speed of item response was found to negatively correlated with accuracy. In particular, Zhan et al. ( 2018 ) found a moderate negative correlation between students' general mathematics ability and speed under a psychometric model for PISA 2012 computer-based mathematics data.

Finally, 1 { R i ( t )>0} , the use of the RESET button, has positive regression coefficients on both final outcome and duration. It implies that the use of RESET button leads to a higher predicted success probability and a longer duration time, given the other features controlled. The connection between the use of the RESET button and the underlying cognitive process of complex problem solving, if it exists, still remains to be investigated.

5. Discussions

5.1. summary.

As an early step toward understanding individuals' complex problem-solving processes, we proposed an event history analysis method for the prediction of the duration and the final outcome of solving a complex problem based on process data. This approach is able to predict at any time t during an individual's problem-solving process, which may be useful in dynamic assessment/learning systems (e.g., in a game-based assessment system). An illustrative example is provided that is based on a CPS item from PISA 2012.

5.2. Inference, Prediction, and Interpretability

As articulated previously, this paper focuses on a prediction problem, rather than a statistical inference problem. Comparing with a prediction framework, statistical inference tends to draw stronger conclusions under stronger assumptions on the data generation mechanism. Unfortunately, due to the complexity of CPS process data, such assumptions are not only hardly satisfied, but also difficult to verify. On the other hand, a prediction framework requires less assumptions and thus is more suitable for exploratory analysis. As a price, the findings from the predictive framework are preliminary and can only be used to generate hypotheses for future studies.

It may be useful to provide uncertainty measures for the prediction performance and for the parameter estimates, where the former indicates the replicability of the prediction performance and the later reflects the stability of the prediction model. In particular, patterns from a prediction model with low replicability and low stability should not be overly interpreted. Such uncertainty measures may be obtained from cross validation and bootstrapping (see Chapter 7, Friedman et al., 2001 ).

It is also worth distinguishing prediction methods based on a simple model like the one proposed above and those based on black-box machine learning algorithms (e.g., random forest). Decisions based on black-box algorithms can be very difficult to understood by human and thus do not provide us insights about the data, even though they may have a high prediction accuracy. On the other hand, a simple model can be regarded as a data dimension reduction tool that extracts interpretable information from data, which may facilitate our understanding of complex problem solving.

5.3. Extending the Current Model

The proposed model can be extended along multiple directions. First, as discussed earlier, we may extend the model by allowing the regression coefficients b jk to be time-dependent. In that case, nonparametric estimation methods (e.g., splines) need to be developed for parameter estimation. In fact, the idea of time-varying coefficients has been intensively investigated in the event history analysis literature (e.g., Fan et al., 1997 ). This extension will be useful if the effects of the features in H i ( t ) change substantially over time.

Second, when the dimension p of H i ( t ) is high, better interpretability and higher prediction power may be achieved by using Lasso-type sparse estimators (see e.g., Chapter 3 Friedman et al., 2001 ). These estimators perform simultaneous feature selection and regularization in order to enhance the prediction accuracy and interpretability.

Finally, outliers are likely to occur in the data due to the abnormal behavioral patterns of a small proportion of people. A better treatment of outliers will lead to better prediction performance. Thus, a more robust objective function will be developed for parameter estimation, by borrowing ideas from the literature of robust statistics (see e.g., Huber and Ronchetti, 2009 ).

5.4. Multiple-Task Analysis

The current analysis focuses on analyzing data from a single task. To study individuals' CPS ability, it may be of more interest to analyze multiple CPS tasks simultaneously and to investigate how an individual's process data from one or multiple tasks predict his/her performance on the other tasks. Generally speaking, one's CPS ability may be better measured by the information in the process data that is generalizable across a representative set of CPS tasks than only his/her final outcomes on these tasks. In this sense, this cross-task prediction problem is closely related to the measurement of CPS ability. This problem is also worth future investigation.

Author Contributions

All authors listed have made a substantial, direct and intellectual contribution to the work, and approved it for publication.

Conflict of Interest Statement

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

1 The item can be found on the OECD website ( http://www.oecd.org/pisa/test-2012/testquestions/question3/ )

2 The log file data and code book for the CC item can be found online: http://www.oecd.org/pisa/pisaproducts/database-cbapisa2012.htm .

Funding. This research was funded by NAEd/Spencer postdoctoral fellowship, NSF grant DMS-1712657, NSF grant SES-1826540, NSF grant IIS-1633360, and NIH grant R01GM047845.

• Allison P. D. (2014). Event history analysis: Regression for longitudinal event data . London: Sage. [ Google Scholar ]
• Danner D., Hagemann D., Schankin A., Hager M., Funke J. (2011). Beyond IQ: a latent state-trait analysis of general intelligence, dynamic decision making, and implicit learning . Intelligence 39 , 323–334. 10.1016/j.intell.2011.06.004 [ CrossRef ] [ Google Scholar ]
• Eichmann B., Goldhammer F., Greiff S., Pucite L., Naumann J. (2019). The role of planning in complex problem solving . Comput. Educ . 128 , 1–12. 10.1016/j.compedu.2018.08.004 [ CrossRef ] [ Google Scholar ]
• Fan J., Gijbels I., King M. (1997). Local likelihood and local partial likelihood in hazard regression . Anna. Statist . 25 , 1661–1690. 10.1214/aos/1031594736 [ CrossRef ] [ Google Scholar ]
• Fox J.-P., Marianti S. (2016). Joint modeling of ability and differential speed using responses and response times . Multivar. Behav. Res . 51 , 540–553. 10.1080/00273171.2016.1171128 [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Friedman J., Hastie T., Tibshirani R. (2001). The Elements of Statistical Learning . New York, NY: Springer. [ Google Scholar ]
• Greiff S., Wüstenberg S., Avvisati F. (2015). Computer-generated log-file analyses as a window into students' minds? A showcase study based on the PISA 2012 assessment of problem solving . Comput. Educ . 91 , 92–105. 10.1016/j.compedu.2015.10.018 [ CrossRef ] [ Google Scholar ]
• Greiff S., Wüstenberg S., Funke J. (2012). Dynamic problem solving: a new assessment perspective . Appl. Psychol. Measur . 36 , 189–213. 10.1177/0146621612439620 [ CrossRef ] [ Google Scholar ]
• Halpin P. F., De Boeck P. (2013). Modelling dyadic interaction with Hawkes processes . Psychometrika 78 , 793–814. 10.1007/s11336-013-9329-1 [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Halpin P. F., von Davier A. A., Hao J., Liu L. (2017). Measuring student engagement during collaboration . J. Educ. Measur . 54 , 70–84. 10.1111/jedm.12133 [ CrossRef ] [ Google Scholar ]
• He Q., von Davier M. (2015). Identifying feature sequences from process data in problem-solving items with N-grams , in Quantitative Psychology Research , eds van der Ark L., Bolt D., Wang W., Douglas J., Wiberg M. (New York, NY: Springer; ), 173–190. [ Google Scholar ]
• He Q., von Davier M. (2016). Analyzing process data from problem-solving items with n-grams: insights from a computer-based large-scale assessment , in Handbook of Research on Technology Tools for Real-World Skill Development , eds Rosen Y., Ferrara S., Mosharraf M. (Hershey, PA: IGI Global; ), 750–777. [ Google Scholar ]
• Huber P. J., Ronchetti E. (2009). Robust Statistics . Hoboken, NJ: John Wiley & Sons. [ Google Scholar ]
• Klein Entink R. H., Kuhn J.-T., Hornke L. F., Fox J.-P. (2009). Evaluating cognitive theory: A joint modeling approach using responses and response times . Psychol. Methods 14 , 54–75. 10.1037/a0014877 [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Luce R. D. (1986). Response Times: Their Role in Inferring Elementary Mental Organization . New York, NY: Oxford University Press. [ Google Scholar ]
• MacKay D. G. (1982). The problems of flexibility, fluency, and speed–accuracy trade-off in skilled behavior . Psychol. Rev . 89 , 483–506. 10.1037/0033-295X.89.5.483 [ CrossRef ] [ Google Scholar ]
• van der Linden W. J. (2007). A hierarchical framework for modeling speed and accuracy on test items . Psychometrika 72 , 287–308. 10.1007/s11336-006-1478-z [ CrossRef ] [ Google Scholar ]
• Vista A., Care E., Awwal N. (2017). Visualising and examining sequential actions as behavioural paths that can be interpreted as markers of complex behaviours . Comput. Hum. Behav . 76 , 656–671. 10.1016/j.chb.2017.01.027 [ CrossRef ] [ Google Scholar ]
• Wüstenberg S., Greiff S., Funke J. (2012). Complex problem solving–More than reasoning? Intelligence 40 , 1–14. 10.1016/j.intell.2011.11.003 [ CrossRef ] [ Google Scholar ]
• Xu H., Fang G., Chen Y., Liu J., Ying Z. (2018). Latent class analysis of recurrent events in problem-solving items . Appl. Psychol. Measur . 42 , 478–498. 10.1177/0146621617748325 [ PMC free article ] [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Yarkoni T., Westfall J. (2017). Choosing prediction over explanation in psychology: lessons from machine learning . Perspect. Psychol. Sci . 12 , 1100–1122. 10.1177/1745691617693393 [ PMC free article ] [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Zhan P., Jiao H., Liao D. (2018). Cognitive diagnosis modelling incorporating item response times . Br. J. Math. Statist. Psychol . 71 , 262–286. 10.1111/bmsp.12114 [ PubMed ] [ CrossRef ] [ Google Scholar ]