Hungarian Method

The Hungarian method is a computational optimization technique that addresses the assignment problem in polynomial time and foreshadows following primal-dual alternatives. In 1955, Harold Kuhn used the term “Hungarian method” to honour two Hungarian mathematicians, Dénes Kőnig and Jenő Egerváry. Let’s go through the steps of the Hungarian method with the help of a solved example.

Hungarian Method to Solve Assignment Problems
The Hungarian method is a simple way to solve assignment problems. Let us first discuss the assignment problems before moving on to learning the Hungarian method.
What is an Assignment Problem?
A transportation problem is a type of assignment problem. The goal is to allocate an equal amount of resources to the same number of activities. As a result, the overall cost of allocation is minimised or the total profit is maximised.
Because available resources such as workers, machines, and other resources have varying degrees of efficiency for executing different activities, and hence the cost, profit, or loss of conducting such activities varies.
Assume we have ‘n’ jobs to do on ‘m’ machines (i.e., one job to one machine). Our goal is to assign jobs to machines for the least amount of money possible (or maximum profit). Based on the notion that each machine can accomplish each task, but at variable levels of efficiency.
Hungarian Method Steps
Check to see if the number of rows and columns are equal; if they are, the assignment problem is considered to be balanced. Then go to step 1. If it is not balanced, it should be balanced before the algorithm is applied.
Step 1 – In the given cost matrix, subtract the least cost element of each row from all the entries in that row. Make sure that each row has at least one zero.
Step 2 – In the resultant cost matrix produced in step 1, subtract the least cost element in each column from all the components in that column, ensuring that each column contains at least one zero.
Step 3 – Assign zeros
- Analyse the rows one by one until you find a row with precisely one unmarked zero. Encircle this lonely unmarked zero and assign it a task. All other zeros in the column of this circular zero should be crossed out because they will not be used in any future assignments. Continue in this manner until you’ve gone through all of the rows.
- Examine the columns one by one until you find one with precisely one unmarked zero. Encircle this single unmarked zero and cross any other zero in its row to make an assignment to it. Continue until you’ve gone through all of the columns.
Step 4 – Perform the Optimal Test
- The present assignment is optimal if each row and column has exactly one encircled zero.
- The present assignment is not optimal if at least one row or column is missing an assignment (i.e., if at least one row or column is missing one encircled zero). Continue to step 5. Subtract the least cost element from all the entries in each column of the final cost matrix created in step 1 and ensure that each column has at least one zero.
Step 5 – Draw the least number of straight lines to cover all of the zeros as follows:
(a) Highlight the rows that aren’t assigned.
(b) Label the columns with zeros in marked rows (if they haven’t already been marked).
(c) Highlight the rows that have assignments in indicated columns (if they haven’t previously been marked).
(d) Continue with (b) and (c) until no further marking is needed.
(f) Simply draw the lines through all rows and columns that are not marked. If the number of these lines equals the order of the matrix, then the solution is optimal; otherwise, it is not.
Step 6 – Find the lowest cost factor that is not covered by the straight lines. Subtract this least-cost component from all the uncovered elements and add it to all the elements that are at the intersection of these straight lines, but leave the rest of the elements alone.
Step 7 – Continue with steps 1 – 6 until you’ve found the highest suitable assignment.
|
|
|---|
Hungarian Method Example
Use the Hungarian method to solve the given assignment problem stated in the table. The entries in the matrix represent each man’s processing time in hours.
\(\begin{array}{l}\begin{bmatrix} & I & II & III & IV & V \\1 & 20 & 15 & 18 & 20 & 25 \\2 & 18 & 20 & 12 & 14 & 15 \\3 & 21 & 23 & 25 & 27 & 25 \\4 & 17 & 18 & 21 & 23 & 20 \\5 & 18 & 18 & 16 & 19 & 20 \\\end{bmatrix}\end{array} \)
With 5 jobs and 5 men, the stated problem is balanced.
\(\begin{array}{l}A = \begin{bmatrix}20 & 15 & 18 & 20 & 25 \\18 & 20 & 12 & 14 & 15 \\21 & 23 & 25 & 27 & 25 \\17 & 18 & 21 & 23 & 20 \\18 & 18 & 16 & 19 & 20 \\\end{bmatrix}\end{array} \)
Subtract the lowest cost element in each row from all of the elements in the given cost matrix’s row. Make sure that each row has at least one zero.
\(\begin{array}{l}A = \begin{bmatrix}5 & 0 & 3 & 5 & 10 \\6 & 8 & 0 & 2 & 3 \\0 & 2 & 4 & 6 & 4 \\0 & 1 & 4 & 6 & 3 \\2 & 2 & 0 & 3 & 4 \\\end{bmatrix}\end{array} \)
Subtract the least cost element in each Column from all of the components in the given cost matrix’s Column. Check to see if each column has at least one zero.
\(\begin{array}{l}A = \begin{bmatrix}5 & 0 & 3 & 3 & 7 \\6 & 8 & 0 & 0 & 0 \\0 & 2 & 4 & 4 & 1 \\0 & 1 & 4 & 4 & 0 \\2 & 2 & 0 & 1 & 1 \\\end{bmatrix}\end{array} \)
When the zeros are assigned, we get the following:
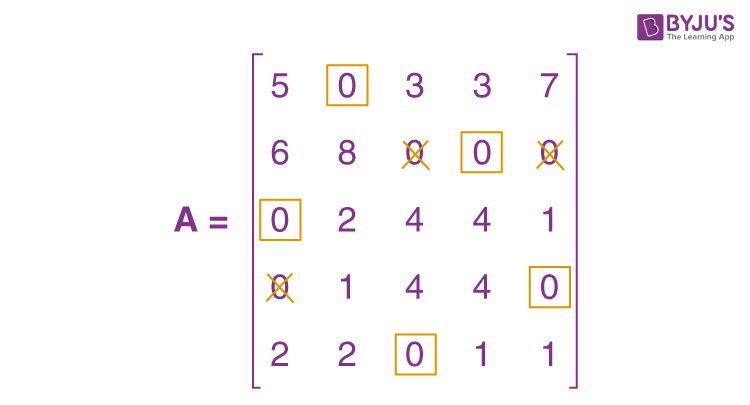
The present assignment is optimal because each row and column contain precisely one encircled zero.
Where 1 to II, 2 to IV, 3 to I, 4 to V, and 5 to III are the best assignments.
Hence, z = 15 + 14 + 21 + 20 + 16 = 86 hours is the optimal time.
Practice Question on Hungarian Method
Use the Hungarian method to solve the following assignment problem shown in table. The matrix entries represent the time it takes for each job to be processed by each machine in hours.
\(\begin{array}{l}\begin{bmatrix}J/M & I & II & III & IV & V \\1 & 9 & 22 & 58 & 11 & 19 \\2 & 43 & 78 & 72 & 50 & 63 \\3 & 41 & 28 & 91 & 37 & 45 \\4 & 74 & 42 & 27 & 49 & 39 \\5 & 36 & 11 & 57 & 22 & 25 \\\end{bmatrix}\end{array} \)
Stay tuned to BYJU’S – The Learning App and download the app to explore all Maths-related topics.
Frequently Asked Questions on Hungarian Method
What is hungarian method.
The Hungarian method is defined as a combinatorial optimization technique that solves the assignment problems in polynomial time and foreshadowed subsequent primal–dual approaches.
What are the steps involved in Hungarian method?
The following is a quick overview of the Hungarian method: Step 1: Subtract the row minima. Step 2: Subtract the column minimums. Step 3: Use a limited number of lines to cover all zeros. Step 4: Add some more zeros to the equation.
What is the purpose of the Hungarian method?
When workers are assigned to certain activities based on cost, the Hungarian method is beneficial for identifying minimum costs.
| MATHS Related Links | |
Leave a Comment Cancel reply
Your Mobile number and Email id will not be published. Required fields are marked *
Request OTP on Voice Call
Post My Comment
Register with BYJU'S & Download Free PDFs
Register with byju's & watch live videos.

How to Solve the Assignment Problem: A Complete Guide
Table of Contents
Assignment problem is a special type of linear programming problem that deals with assigning a number of resources to an equal number of tasks in the most efficient way. The goal is to minimize the total cost of assignments while ensuring that each task is assigned to only one resource and each resource is assigned to only one task. In this blog, we will discuss the solution of the assignment problem using the Hungarian method, which is a popular algorithm for solving the problem.
Understanding the Assignment Problem
Before we dive into the solution, it is important to understand the problem itself. In the assignment problem, we have a matrix of costs, where each row represents a resource and each column represents a task. The objective is to assign each resource to a task in such a way that the total cost of assignments is minimized. However, there are certain constraints that need to be satisfied – each resource can be assigned to only one task and each task can be assigned to only one resource.
Solving the Assignment Problem
There are various methods for solving the assignment problem, including the Hungarian method, the brute force method, and the auction algorithm. Here, we will focus on the steps involved in solving the assignment problem using the Hungarian method, which is the most commonly used and efficient method.
Step 1: Set up the cost matrix
The first step in solving the assignment problem is to set up the cost matrix, which represents the cost of assigning a task to an agent. The matrix should be square and have the same number of rows and columns as the number of tasks and agents, respectively.
Step 2: Subtract the smallest element from each row and column
To simplify the calculations, we need to reduce the size of the cost matrix by subtracting the smallest element from each row and column. This step is called matrix reduction.
Step 3: Cover all zeros with the minimum number of lines
The next step is to cover all zeros in the matrix with the minimum number of horizontal and vertical lines. This step is called matrix covering.
Step 4: Test for optimality and adjust the matrix
To test for optimality, we need to calculate the minimum number of lines required to cover all zeros in the matrix. If the number of lines equals the number of rows or columns, the solution is optimal. If not, we need to adjust the matrix and repeat steps 3 and 4 until we get an optimal solution.
Step 5: Assign the tasks to the agents
The final step is to assign the tasks to the agents based on the optimal solution obtained in step 4. This will give us the most cost-effective or profit-maximizing assignment.
Solution of the Assignment Problem using the Hungarian Method
The Hungarian method is an algorithm that uses a step-by-step approach to find the optimal assignment. The algorithm consists of the following steps:
- Subtract the smallest entry in each row from all the entries of the row.
- Subtract the smallest entry in each column from all the entries of the column.
- Draw the minimum number of lines to cover all zeros in the matrix. If the number of lines drawn is equal to the number of rows, we have an optimal solution. If not, go to step 4.
- Determine the smallest entry not covered by any line. Subtract it from all uncovered entries and add it to all entries covered by two lines. Go to step 3.
The above steps are repeated until an optimal solution is obtained. The optimal solution will have all zeros covered by the minimum number of lines. The assignments can be made by selecting the rows and columns with a single zero in the final matrix.
Applications of the Assignment Problem
The assignment problem has various applications in different fields, including computer science, economics, logistics, and management. In this section, we will provide some examples of how the assignment problem is used in real-life situations.
Applications in Computer Science
The assignment problem can be used in computer science to allocate resources to different tasks, such as allocating memory to processes or assigning threads to processors.
Applications in Economics
The assignment problem can be used in economics to allocate resources to different agents, such as allocating workers to jobs or assigning projects to contractors.
Applications in Logistics
The assignment problem can be used in logistics to allocate resources to different activities, such as allocating vehicles to routes or assigning warehouses to customers.
Applications in Management
The assignment problem can be used in management to allocate resources to different projects, such as allocating employees to tasks or assigning budgets to departments.
Let’s consider the following scenario: a manager needs to assign three employees to three different tasks. Each employee has different skills, and each task requires specific skills. The manager wants to minimize the total time it takes to complete all the tasks. The skills and the time required for each task are given in the table below:
| Task 1 | Task 2 | Task 3 | |
|---|---|---|---|
| Emp 1 | 5 | 7 | 6 |
| Emp 2 | 6 | 4 | 5 |
| Emp 3 | 8 | 5 | 3 |
The assignment problem is to determine which employee should be assigned to which task to minimize the total time required. To solve this problem, we can use the Hungarian method, which we discussed in the previous blog.
Using the Hungarian method, we first subtract the smallest entry in each row from all the entries of the row:
| Task 1 | Task 2 | Task 3 | |
|---|---|---|---|
| Emp 1 | 0 | 2 | 1 |
| Emp 2 | 2 | 0 | 1 |
| Emp 3 | 5 | 2 | 0 |
Next, we subtract the smallest entry in each column from all the entries of the column:
| Task 1 | Task 2 | Task 3 | |
|---|---|---|---|
| Emp 1 | 0 | 2 | 1 |
| Emp 2 | 2 | 0 | 1 |
| Emp 3 | 5 | 2 | 0 |
| 0 | 0 | 0 |
We draw the minimum number of lines to cover all the zeros in the matrix, which in this case is three:
Since the number of lines is equal to the number of rows, we have an optimal solution. The assignments can be made by selecting the rows and columns with a single zero in the final matrix. In this case, the optimal assignments are:
- Emp 1 to Task 3
- Emp 2 to Task 2
- Emp 3 to Task 1
This assignment results in a total time of 9 units.
I hope this example helps you better understand the assignment problem and how to solve it using the Hungarian method.
Solving the assignment problem may seem daunting, but with the right approach, it can be a straightforward process. By following the steps outlined in this guide, you can confidently tackle any assignment problem that comes your way.
How useful was this post?
Click on a star to rate it!
Average rating 0 / 5. Vote count: 0
No votes so far! Be the first to rate this post.
We are sorry that this post was not useful for you! 😔
Let us improve this post!
Tell us how we can improve this post?
Operations Research
1 Operations Research-An Overview
- History of O.R.
- Approach, Techniques and Tools
- Phases and Processes of O.R. Study
- Typical Applications of O.R
- Limitations of Operations Research
- Models in Operations Research
- O.R. in real world
2 Linear Programming: Formulation and Graphical Method
- General formulation of Linear Programming Problem
- Optimisation Models
- Basics of Graphic Method
- Important steps to draw graph
- Multiple, Unbounded Solution and Infeasible Problems
- Solving Linear Programming Graphically Using Computer
- Application of Linear Programming in Business and Industry
3 Linear Programming-Simplex Method
- Principle of Simplex Method
- Computational aspect of Simplex Method
- Simplex Method with several Decision Variables
- Two Phase and M-method
- Multiple Solution, Unbounded Solution and Infeasible Problem
- Sensitivity Analysis
- Dual Linear Programming Problem
4 Transportation Problem
- Basic Feasible Solution of a Transportation Problem
- Modified Distribution Method
- Stepping Stone Method
- Unbalanced Transportation Problem
- Degenerate Transportation Problem
- Transhipment Problem
- Maximisation in a Transportation Problem
5 Assignment Problem
- Solution of the Assignment Problem
- Unbalanced Assignment Problem
- Problem with some Infeasible Assignments
- Maximisation in an Assignment Problem
- Crew Assignment Problem
6 Application of Excel Solver to Solve LPP
- Building Excel model for solving LP: An Illustrative Example
7 Goal Programming
- Concepts of goal programming
- Goal programming model formulation
- Graphical method of goal programming
- The simplex method of goal programming
- Using Excel Solver to Solve Goal Programming Models
- Application areas of goal programming
8 Integer Programming
- Some Integer Programming Formulation Techniques
- Binary Representation of General Integer Variables
- Unimodularity
- Cutting Plane Method
- Branch and Bound Method
- Solver Solution
9 Dynamic Programming
- Dynamic Programming Methodology: An Example
- Definitions and Notations
- Dynamic Programming Applications
10 Non-Linear Programming
- Solution of a Non-linear Programming Problem
- Convex and Concave Functions
- Kuhn-Tucker Conditions for Constrained Optimisation
- Quadratic Programming
- Separable Programming
- NLP Models with Solver
11 Introduction to game theory and its Applications
- Important terms in Game Theory
- Saddle points
- Mixed strategies: Games without saddle points
- 2 x n games
- Exploiting an opponent’s mistakes
12 Monte Carlo Simulation
- Reasons for using simulation
- Monte Carlo simulation
- Limitations of simulation
- Steps in the simulation process
- Some practical applications of simulation
- Two typical examples of hand-computed simulation
- Computer simulation
13 Queueing Models
- Characteristics of a queueing model
- Notations and Symbols
- Statistical methods in queueing
- The M/M/I System
- The M/M/C System
- The M/Ek/I System
- Decision problems in queueing
Assignment Problem: Meaning, Methods and Variations | Operations Research
After reading this article you will learn about:- 1. Meaning of Assignment Problem 2. Definition of Assignment Problem 3. Mathematical Formulation 4. Hungarian Method 5. Variations.
Meaning of Assignment Problem:
An assignment problem is a particular case of transportation problem where the objective is to assign a number of resources to an equal number of activities so as to minimise total cost or maximize total profit of allocation.
The problem of assignment arises because available resources such as men, machines etc. have varying degrees of efficiency for performing different activities, therefore, cost, profit or loss of performing the different activities is different.
Thus, the problem is “How should the assignments be made so as to optimize the given objective”. Some of the problem where the assignment technique may be useful are assignment of workers to machines, salesman to different sales areas.
Definition of Assignment Problem:
ADVERTISEMENTS:
Suppose there are n jobs to be performed and n persons are available for doing these jobs. Assume that each person can do each job at a term, though with varying degree of efficiency, let c ij be the cost if the i-th person is assigned to the j-th job. The problem is to find an assignment (which job should be assigned to which person one on-one basis) So that the total cost of performing all jobs is minimum, problem of this kind are known as assignment problem.
The assignment problem can be stated in the form of n x n cost matrix C real members as given in the following table:
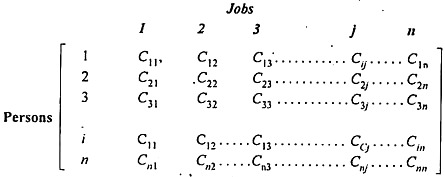
On small screens, scroll horizontally to view full calculation
| Job | ||||
|---|---|---|---|---|
| Person | 1 | 2 | 3 | 4 |
| A | 0 | 5 | 2 | 8 |
| B | 0 | 3 | 8 | 2 |
| C | 2 | 0 | 4 | 7 |
| D | 2 | 0 | 1 | 1 |
Identify the minimum element in each column and subtract it from every element of that column.
| Job | ||||
|---|---|---|---|---|
| Person | 1 | 2 | 3 | 4 |
| A | 0 | 5 | 1 | 7 |
| B | 0 | 3 | 7 | 1 |
| C | 2 | 0 | 3 | 6 |
| D | 2 | 0 | 0 | 0 |
Make the assignments for the reduced matrix obtained from steps 1 and 2 in the following way:
- For every zero that becomes assigned, cross out (X) all other zeros in the same row and the same column.
- If for a row and a column, there are two or more zeros and one cannot be chosen by inspection, choose the cell arbitrarily for assignment.
An optimal assignment is found, if the number of assigned cells equals the number of rows (and columns). In case you have chosen a zero cell arbitrarily, there may be alternate optimal solutions. If no optimal solution is found, go to step 5.
Use Horizontal Scrollbar to View Full Table Calculation
| Job | ||||
|---|---|---|---|---|
| Person | 1 | 2 | 3 | 4 |
| A | 5 | 1 | 7 | |
| B | 3 | 7 | 1 | |
| C | 2 | 3 | 6 | |
| D | 2 | |||
Draw the minimum number of vertical and horizontal lines necessary to cover all the zeros in the reduced matrix obtained from step 3 by adopting the following procedure:
- Mark all the rows that do not have assignments.
- Mark all the columns (not already marked) which have zeros in the marked rows.
- Mark all the rows (not already marked) that have assignments in marked columns.
- Repeat steps 5 (ii) and (iii) until no more rows or columns can be marked.
- Draw straight lines through all unmarked rows and marked columns.
You can also draw the minimum number of lines by inspection.
Select the smallest element (i.e., 1) from all the uncovered elements. Subtract this smallest element from all the uncovered elements and add it to the elements, which lie at the intersection of two lines. Thus, we obtain another reduced matrix for fresh assignment.
| Job | ||||
|---|---|---|---|---|
| Person | 1 | 2 | 3 | 4 |
| A | 0 | 4 | 0 | 6 |
| B | 0 | 2 | 6 | 0 |
| C | 3 | 0 | 3 | 6 |
| D | 3 | 0 | 0 | 0 |
Now again make the assignments for the reduced matrix.
Final Table: Hungarian Method
| Job | ||||
|---|---|---|---|---|
| Person | 1 | 2 | 3 | 4 |
| A | 4 | 6 | ||
| B | 2 | 6 | ||
| C | 3 | 3 | 6 | |
| D | 3 | |||
Since the number of assignments is equal to the number of rows (& columns), this is the optimal solution.
The total cost of assignment = A1 + B4 + C2 + D3
Substituting values from original table: 20 + 17 + 17 + 24 = Rs. 78.
Share This Article
Operations Research Simplified Back Next
Goal programming Linear programming Simplex Method Transportation Problem
Operations Research by P. Mariappan
Get full access to Operations Research and 60K+ other titles, with a free 10-day trial of O'Reilly.
There are also live events, courses curated by job role, and more.
Assignment Problem
5.1 introduction.
The assignment problem is one of the special type of transportation problem for which more efficient (less-time consuming) solution method has been devised by KUHN (1956) and FLOOD (1956). The justification of the steps leading to the solution is based on theorems proved by Hungarian mathematicians KONEIG (1950) and EGERVARY (1953), hence the method is named Hungarian.
5.2 GENERAL MODEL OF THE ASSIGNMENT PROBLEM
Consider n jobs and n persons. Assume that each job can be done only by one person and the time a person required for completing the i th job (i = 1,2,...n) by the j th person (j = 1,2,...n) is denoted by a real number C ij . On the whole this model deals with the assignment of n candidates to n jobs ...
Get Operations Research now with the O’Reilly learning platform.
O’Reilly members experience books, live events, courses curated by job role, and more from O’Reilly and nearly 200 top publishers.
Don’t leave empty-handed
Get Mark Richards’s Software Architecture Patterns ebook to better understand how to design components—and how they should interact.
It’s yours, free.

Check it out now on O’Reilly
Dive in for free with a 10-day trial of the O’Reilly learning platform—then explore all the other resources our members count on to build skills and solve problems every day.

Algorithms: The Assignment Problem
One of the interesting things about studying optimization is that the techniques show up in a lot of different areas. The “assignment problem” is one that can be solved using simple techniques, at least for small problem sizes, and is easy to see how it could be applied to the real world.
Assignment Problem
Pretend for a moment that you are writing software for a famous ride sharing application. In a crowded environment, you might have multiple prospective customers that are requesting service at the same time, and nearby you have multiple drivers that can take them where they need to go. You want to assign the drivers to the customers in a way that minimizes customer wait time (so you keep the customers happy) and driver empty time (so you keep the drivers happy).
The assignment problem is designed for exactly this purpose. We start with m agents and n tasks. We make the rule that every agent has to be assigned to a task. For each agent-task pair, we figure out a cost associated to have that agent perform that task. We then figure out which assignment of agents to tasks minimizes the total cost.
Of course, it may be true that m != n , but that’s OK. If there are too many tasks, we can make up a “dummy” agent that is more expensive than any of the others. This will ensure that the least desirable task will be left to the dummy agent, and we can remove that from the solution. Or, if there are too many agents, we can make up a “dummy” task that is free for any agent. This will ensure that the agent with the highest true cost will get the dummy task, and will be idle.
If that last paragraph was a little dense, don’t worry; there’s an example coming that will help show how it works.
There are special algorithms for solving assignment problems, but one thing that’s nice about them is that a general-purpose solver can handle them too. Below is an example, but first it will help to cover a few concepts that we’ll be using.
Optimization Problems
Up above, we talked about making “rules” and minimizing costs. The usual name for this is optimization. An optimization problem is one where we have an “objective function” (which tells us what our goals are) and one or more “constraint functions” (which tell us what the rules are). The classic example is a factory that can make both “widgets” and “gadgets”. Each “widget” and “gadget” earns a certain amount of profit, but it also uses up raw material and time on the factory’s machines. The optimization problem is to determine exactly how many “widgets” and how many “gadgets” to make to maximize profit (the objective) while fitting within the material and time available (the constraints).
If we were to write this simple optimization problem out, it might look like this:
In this case, we have two variables: g for the number of gadgets we make and w for the number of widgets we make. We also have three constraints that we have to meet. Note that they are inequalities; we might not use all the available material or time in our optimal solution.
Just to unpack this a little: in English, the above is saying that we make 45 dollars / euros / quatloos per gadget we make. However, to make a gadget needs 120 lbs of raw material 1, 80 lbs of raw material 2, and 3.8 hours of machine time. So there is a limit on how many gadgets we can make, and it might be a better use of resources to balance gadgets with widgets.
Of course, real optimization problems have many more than two variables and many constraint functions, making them much harder to solve. The easiest kind of optimization problem to solve is linear, and fortunately, the assignment problem is linear.
Linear Programming
A linear program is a kind of optimization problem where both the objective function and the constraint functions are linear. (OK, that definition was a little self-referential.) We can have as many variables as we want, and as many constraint functions as we want, but none of the variables can have exponents in any of the functions. This limitation allows us to apply very efficient mathematical approaches to solve the problem, even for very large problems.
We can state the assignment problem as a linear programming problem. First, we choose to make “i” represent each of our agents (drivers) and “j” to represent each of our tasks (customers). Now, to write a problem like this, we need variables. The best approach is to use “indicator” variables, where xij = 1 means “driver i picks up customer j” and xij = 0 means “driver i does not pick up customer j”.
We wind up with:
This is a compact mathematical way to describe the problem, so again let me put it in English.
First, we need to figure out the cost of having each driver pick up each customer. Then, we can calculate the total cost for any scenario by just adding up the costs for the assignments we pick. For any assignment we don’t pick, xij will equal zero, so that term will just drop out of the sum.
Of course, the way we set up the objective function, the cheapest solution is for no drivers to pick up any customers. That’s not a very good business model. So we need a constraint to show that we want to have a driver assigned to every customer. At the same time, we can’t have a driver assigned to mutiple customers. So we need a constraint for that too. That leads us to the two constraints in the problem. The first just says, if you add up all the assignments for a given driver, you want the total number of assignments for that driver to be exactly one. The second constraint says, if you add up all the assignments to a given customer, you want the total number of drivers assigned to the customer to be one. If you have both of these, then each driver is assigned to exactly one customer, and the customers and drivers are happy. If you do it in a way that minimizes costs, then the business is happy too.
Solving with Octave and GLPK
The GNU Linear Programming Kit is a library that solves exactly these kinds of problems. It’s easy to set up the objective and constraints using GNU Octave and pass these over to GLPK for a solution.
Given some made-up sample data, the program looks like this:
Start with the definition of “c”, the cost information. For this example, I chose to have four drivers and three customers. There are sixteen numbers there; the first four are the cost of each driver to get the first customer, the next four are for the second customer, and the next four are for the third customer. Because we have an extra driver, we add a “dummy” customer at the end that is zero cost. This represents one of the drivers being idle.
The next definition is “b”, the right-hand side of our constraints. There are eight constraints, one for each of the drivers, and one for each of the customers (including the dummy). For each constraint, the right-hand side is 1.
The big block in the middle defines our constraint matrix “a”. This is the most challenging part of taking the mathematical definition and putting it into a form that is usable by GLPK; we have to expand out each constraint. Fortunately, in these kinds of cases, we tend to get pretty patterns that help us know we’re on the right track.
The first line in “a” says that the first customer needs a driver. To see why, remember that in our cost information, the first four numbers are the cost for each driver to get the first customer. With this constraint, we are requiring that one of those four costs be included and therefore that a driver is “selected” for the first customer. The other lines in “a” work similarly; the last four ensure that each driver has an assignment.
Note that the number of rows in “a” matches the number of items in “b”, and the number of columns in “a” matches the number of items in “c”. This is important; GLPK won’t run if this is not true (and our problem isn’t stated right in any case).
Compared to the above, the last few lines are easy.
- “lb” gives the lower bound for each variable.
- “ub” gives the upper bound.
- “ctype” tells GLPK that each constraint is an equality (“strict” as opposed to providing a lower or upper bound).
- “vartype” tells GLPK that these variables are all integers (can’t have half a driver showing up).
- “s” tells GLPK that we want to minimize our costs, not maximize them.
We push all that through a function call to GLPK, and what comes back are two values (along with some other stuff I’ll exclude for clarity):
The first item tells us that our best solution takes 27 minutes, or dollars, or whatever unit we used for cost. The second item tells us the assignments we got. (Note for pedants: I transposed this output to save space.)
This output tells us that customer 1 gets driver 2, customer 2 gets driver 3, customer 3 gets driver 4, and driver 1 is idle. If you look back at the cost data, you can see this makes sense, because driver 1 had some of the most expensive times to the three customers. You can also see that it managed to pick the least expensive pairing for each customer. (Of course, if I had done a better job making up cost data, it might not have picked the least expensive pairing in all cases, because a suboptimal individual pairing might still lead to an overall optimal solution. But this is a toy example.)
Of course, for a real application, we would have to take into consideration many other factors, such as the passage of time. Rather than knowing all of our customers and drivers up front, we would have customers and drivers continually showing up and being assigned. But I hope this simple example has revealed some of the concepts behind optimization and linear programming and the kinds of real-world problems that can be solved.
Assignment problem: Hungarian method 3

Assignment problem: Hungarian Method Nui Ruppert (Mtk_Nr.: 373224) David Lenh (Mtk_Nr.: 368343) Amir Farshchi Tabrizi (Mtk-Nr.: 372894)
In this OR-Wiki entry we're going to explain the Hungarian method with 3 examples. In the first example you'll find the optimal solution after a few steps with the help of the reduced matrix. The second example illustrates a complex case where you need to proceed all the steps of the algorithm to get to an optimal solution. Finally in the third example we will show how to solve a maximization problem with the Hungarian method.
Inhaltsverzeichnis
- 1 Introduction
- 2 Example 1 – Minimization problem
- 3 Example 2 – Minimazation problem
- 4 Example 3 – Maximization problem
- 6 References
Introduction
The Hungarian method is a combinatorial optimization algorithm which was developed and published by Harold Kuhn in 1955. This method was originally invented for the best assignment of a set of persons to a set of jobs. It is a special case of the transportation problem. The algorithm finds an optimal assignment for a given “n x n” cost matrix. “Assignment problems deal with the question how to assign n items (e.g. jobs) to n machines (or workers) in the best possible way. […] Mathematically an assignment is nothing else than a bijective mapping of a finite set into itself […]” [1]
The assignment constraints are mathematically defined as:
To make clear how to solve an assignment problem with the Hungarian algorithm we will show you the different cases with several examples which can occur .
Example 1 – Minimization problem
In this example we have to assign 4 workers to 4 machines. Each worker causes different costs for the machines. Your goal is to minimize the total cost to the condition that each machine goes to exactly 1 person and each person works at exactly 1 machine. For comprehension: Worker 1 causes a cost of 6 for machine 1 and so on …
To solve the problem we have to perform the following steps:
Step 1 – Subtract the row minimum from each row.
Step 2 – Subtract the column minimum from each column from the reduced matrix.
The idea behind these 2 steps is to simplify the matrix since the solution of the reduced matrix will be exactly the same as of the original matrix.
Step 3 – Assign one “0” to each row & column.
Now that we have simplified the matrix we can assign each worker with the minimal cost to each machine which is represented by a “0”.
- In the first row we have one assignable “0” therefore we assign it to worker 3 .
- In the second row we also only have one assignable “0” therefore we assign it to worker 4 .
- In the third row we have two assignable “0”. We leave it as it is for now.
- In the fourth row we have one assignable “0” therefore we assign it. Consider that we can only assign each worker to each machine hence we can’t allocate any other “0” in the first column.
- Now we go back to the third row which now only has one assignable “0” for worker 2 .
As soon as we can assign each worker to one machine, we have the optimal solution . In this case there is no need to proceed any further steps. Remember also, if we decide on an arbitrary order in which we start allocating the “0”s then we may get into a situation where we have 3 assignments as against the possible 4. If we assign a “0” in the third row to worker 1 we wouldn’t be able to allocate any “0”s in column one and row two.
The rule to assign the “0”:
- If there is an assignable “0”, only 1 assignable “0” in any row or any column, assign it.
- If there are more than 1, leave it and proceed.
This rule would try to give us as many assignments as possible.
Now there are also cases where you won’t get an optimal solution for a reduced matrix after one iteration. The following example will explain it.
Example 2 – Minimazation problem
In this example we have the fastest taxi company that has to assign each taxi to each passenger as fast as possible. The numbers in the matrix represent the time to reach the passenger.
We proceed as in the first example.
Iteration 1:
Now we have to assign the “0”s for every row respectively to the rule that we described earlier in example 1.
- In the first row we have one assignable “0” therefore we assign it and no other allocation in column 2 is possible.
- In the second row we have one assignable “0” therefore we assign it.
- In the third row we have several assignable “0”s. We leave it as it is for now and proceed.
- In the fourth and fifth row we have no assignable “0”s.
Now we proceed with the allocations of the “0”s for each column .
- In the first column we have one assignable “0” therefore we assign it. No other “0”s in row 3 are assignable anymore.
Now we are unable to proceed because all the “0”s either been assigned or crossed. The crosses indicate that they are not fit for assignments because assignments are already made.
We realize that we have 3 assignments for this 5x5 matrix. In the earlier example we were able to get 4 assignments for a 4x4 matrix. Now we have to follow another procedure to get the remaining 2 assignments (“0”).
Step 4 – Tick all unassigned rows.
Step 5 – If a row is ticked and has a “0”, then tick the corresponding column (if the column is not yet ticked).
Step 6 – If a column is ticked and has an assignment, then tick the corresponding row (if the row is not yet ticked).
Step 7 - Repeat step 5 and 6 till no more ticking is possible.
In this case there is no more ticking possible and we proceed with the next step.
Step 8 – Draw lines through unticked rows and ticked columns. The number of lines represents the maximum number of assignments possible.
Step 9 – Find out the smallest number which does not have any line passing through it. We call it Theta. Subtract theta from all the numbers that do not have any lines passing through them and add theta to all those numbers that have two lines passing through them. Keep the rest of them the same.
(With this step we create a new “0”)
With the new assignment matrix we start to assign the “0”s after the explained rules. Nevertheless we have 4 assignments against the required 5 for an optimal solution. Therefore we have to repeat step 4 – 9.
Iteration 2:
Step 4 – Tick all unassigned row.
Note: The indices of the ticks show you the order we added them.
Iteration 3:
Iteration 4:
After the fourth iteration we assign the “0”s again and now we have an optimal solution with 5 assignments.
The solution:
- Taxi1 => Passenger1 - duration 12
- Taxi2 => Passenger4 - duration 11
- Taxi3 => Passenger2 - duration 8
- Taxi4 => Passenger3 - duration 14
- Taxi5 => Passenger5 - duration 11
If we define the needed duration as costs, the minimal cost for this problem is 56.
Example 3 – Maximization problem
Furthermore the Hungarian algorithm can also be used for a maximization problem in which case we first have to transform the matrix. For example a company wants to assign different workers to different machines. Each worker is more or less efficient with each machine. The efficiency can be defined as profit. The higher the number, the higher the profit.
As you can see, the maximal profit of the matrix is 13. The simple twist that we do is rather than try to maximize the profit, we’re going to try to minimize the profit that you don’t get. If every value is taken away from 13, then we can minimize the amount of profit lost. We receive the following matrix:
From now on we proceed as usual with the steps to get to an optimal solution.
With the determined optimal solution we can compute the maximal profit:
- Worker1 => Machine2 - 9
- Worker2 => Machine4 - 11
- Worker3 => Machine3 - 13
- Worker4 => Machine1 - 7
Maximal profit is 40.
The optimal solution is found if there is one assigned “0” for each row and each column.
[1] Linear Assignment Problems and Extensions, Rainer E. Burkard, Eranda Cela
[2] Operations Research Skript TU Kaiserslautern, Prof. Dr. Oliver Wendt
[3] The Hungarian method for the assignment problem, H. W. Kuhn, Bryn Mawr College
Fundamental of Operations Research, Lec. 16, Prof. G. Srinivasan

Navigationsmenü
- Quelltext anzeigen
- Versionsgeschichte
Meine Werkzeuge
- Gemeinschaftsportal
- Operations Research
- Studentenbeiträge zum Thema Operations Research
- Wirtschaftsinformatik
- Aktuelle Ereignisse
- Letzte Änderungen
- Zufällige Seite
- Links auf diese Seite
- Änderungen an verlinkten Seiten
- Spezialseiten
- Druckversion
- Permanenter Link
- Seiteninformationen
- Diese Seite wurde zuletzt am 1. Juli 2013 um 11:03 Uhr geändert.
- Datenschutz
- Über Operations-Research-Wiki

In order to continue enjoying our site, we ask that you confirm your identity as a human. Thank you very much for your cooperation.

- Google OR-Tools
- Español – América Latina
- Português – Brasil
- Tiếng Việt
Solving an Assignment Problem
This section presents an example that shows how to solve an assignment problem using both the MIP solver and the CP-SAT solver.
In the example there are five workers (numbered 0-4) and four tasks (numbered 0-3). Note that there is one more worker than in the example in the Overview .
The costs of assigning workers to tasks are shown in the following table.
| Worker | Task 0 | Task 1 | Task 2 | Task 3 |
|---|---|---|---|---|
| 90 | 80 | 75 | 70 | |
| 35 | 85 | 55 | 65 | |
| 125 | 95 | 90 | 95 | |
| 45 | 110 | 95 | 115 | |
| 50 | 100 | 90 | 100 |
The problem is to assign each worker to at most one task, with no two workers performing the same task, while minimizing the total cost. Since there are more workers than tasks, one worker will not be assigned a task.
MIP solution
The following sections describe how to solve the problem using the MPSolver wrapper .
Import the libraries
The following code imports the required libraries.
Create the data
The following code creates the data for the problem.
The costs array corresponds to the table of costs for assigning workers to tasks, shown above.
Declare the MIP solver
The following code declares the MIP solver.
Create the variables
The following code creates binary integer variables for the problem.
Create the constraints
Create the objective function.
The following code creates the objective function for the problem.
The value of the objective function is the total cost over all variables that are assigned the value 1 by the solver.
Invoke the solver
The following code invokes the solver.
Print the solution
The following code prints the solution to the problem.
Here is the output of the program.
Complete programs
Here are the complete programs for the MIP solution.
CP SAT solution
The following sections describe how to solve the problem using the CP-SAT solver.
Declare the model
The following code declares the CP-SAT model.
The following code sets up the data for the problem.
The following code creates the constraints for the problem.
Here are the complete programs for the CP-SAT solution.
Except as otherwise noted, the content of this page is licensed under the Creative Commons Attribution 4.0 License , and code samples are licensed under the Apache 2.0 License . For details, see the Google Developers Site Policies . Java is a registered trademark of Oracle and/or its affiliates.
Last updated 2023-01-02 UTC.
Index Assignment problem Hungarian algorithm Solve online
The Hungarian algorithm
The Hungarian algorithm consists of the four steps below. The first two steps are executed once, while Steps 3 and 4 are repeated until an optimal assignment is found. The input of the algorithm is an n by n square matrix with only nonnegative elements.
Step 1: Subtract row minima
For each row, find the lowest element and subtract it from each element in that row.
Step 2: Subtract column minima
Similarly, for each column, find the lowest element and subtract it from each element in that column.
Step 3: Cover all zeros with a minimum number of lines
Cover all zeros in the resulting matrix using a minimum number of horizontal and vertical lines. If n lines are required, an optimal assignment exists among the zeros. The algorithm stops.
If less than n lines are required, continue with Step 4.
Step 4: Create additional zeros
Find the smallest element (call it k ) that is not covered by a line in Step 3. Subtract k from all uncovered elements, and add k to all elements that are covered twice.
Continue with:
The Hungarian algorithm explained based on an example.
The Hungarian algorithm explained based on a self chosen or on a random cost matrix.
HungarianAlgorithm.com © 2013-2024
- Data Structures
- Linked List
- Binary Tree
- Binary Search Tree
- Segment Tree
- Disjoint Set Union
- Fenwick Tree
- Red-Black Tree
- Advanced Data Structures
Hungarian Algorithm for Assignment Problem | Set 2 (Implementation)
Given a 2D array , arr of size N*N where arr[i][j] denotes the cost to complete the j th job by the i th worker. Any worker can be assigned to perform any job. The task is to assign the jobs such that exactly one worker can perform exactly one job in such a way that the total cost of the assignment is minimized.
Input: arr[][] = {{3, 5}, {10, 1}} Output: 4 Explanation: The optimal assignment is to assign job 1 to the 1st worker, job 2 to the 2nd worker. Hence, the optimal cost is 3 + 1 = 4. Input: arr[][] = {{2500, 4000, 3500}, {4000, 6000, 3500}, {2000, 4000, 2500}} Output: 4 Explanation: The optimal assignment is to assign job 2 to the 1st worker, job 3 to the 2nd worker and job 1 to the 3rd worker. Hence, the optimal cost is 4000 + 3500 + 2000 = 9500.
Different approaches to solve this problem are discussed in this article .
Approach: The idea is to use the Hungarian Algorithm to solve this problem. The algorithm is as follows:
- For each row of the matrix, find the smallest element and subtract it from every element in its row.
- Repeat the step 1 for all columns.
- Cover all zeros in the matrix using the minimum number of horizontal and vertical lines.
- Test for Optimality : If the minimum number of covering lines is N , an optimal assignment is possible. Else if lines are lesser than N , an optimal assignment is not found and must proceed to step 5.
- Determine the smallest entry not covered by any line. Subtract this entry from each uncovered row, and then add it to each covered column. Return to step 3.
Consider an example to understand the approach:
Let the 2D array be: 2500 4000 3500 4000 6000 3500 2000 4000 2500 Step 1: Subtract minimum of every row. 2500, 3500 and 2000 are subtracted from rows 1, 2 and 3 respectively. 0 1500 1000 500 2500 0 0 2000 500 Step 2: Subtract minimum of every column. 0, 1500 and 0 are subtracted from columns 1, 2 and 3 respectively. 0 0 1000 500 1000 0 0 500 500 Step 3: Cover all zeroes with minimum number of horizontal and vertical lines. Step 4: Since we need 3 lines to cover all zeroes, the optimal assignment is found. 2500 4000 3500 4000 6000 3500 2000 4000 2500 So the optimal cost is 4000 + 3500 + 2000 = 9500
For implementing the above algorithm, the idea is to use the max_cost_assignment() function defined in the dlib library . This function is an implementation of the Hungarian algorithm (also known as the Kuhn-Munkres algorithm) which runs in O(N 3 ) time. It solves the optimal assignment problem.
Below is the implementation of the above approach:
Time Complexity: O(N 3 ) Auxiliary Space: O(N 2 )
Please Login to comment...
Similar reads.
- Mathematical
Improve your Coding Skills with Practice
What kind of Experience do you want to share?
Procedure, Example Solved Problem | Operations Research - Solution of assignment problems (Hungarian Method) | 12th Business Maths and Statistics : Chapter 10 : Operations Research
Chapter: 12th business maths and statistics : chapter 10 : operations research.
Solution of assignment problems (Hungarian Method)
First check whether the number of rows is equal to the numbers of columns, if it is so, the assignment problem is said to be balanced.
Step :1 Choose the least element in each row and subtract it from all the elements of that row.
Step :2 Choose the least element in each column and subtract it from all the elements of that column. Step 2 has to be performed from the table obtained in step 1.
Step:3 Check whether there is atleast one zero in each row and each column and make an assignment as follows.
Step :4 If each row and each column contains exactly one assignment, then the solution is optimal.
Example 10.7
Solve the following assignment problem. Cell values represent cost of assigning job A, B, C and D to the machines I, II, III and IV.

Here the number of rows and columns are equal.
∴ The given assignment problem is balanced. Now let us find the solution.
Step 1: Select a smallest element in each row and subtract this from all the elements in its row.
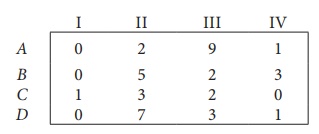
Look for atleast one zero in each row and each column.Otherwise go to step 2.
Step 2: Select the smallest element in each column and subtract this from all the elements in its column.

Since each row and column contains atleast one zero, assignments can be made.
Step 3 (Assignment):
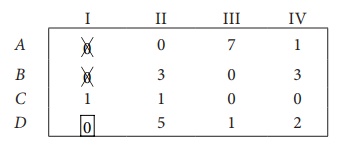
Thus all the four assignments have been made. The optimal assignment schedule and total cost is
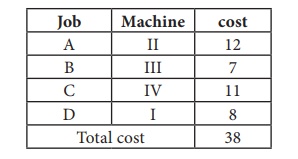
The optimal assignment (minimum) cost
Example 10.8
Consider the problem of assigning five jobs to five persons. The assignment costs are given as follows. Determine the optimum assignment schedule.
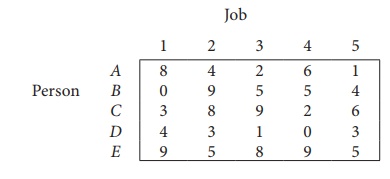
∴ The given assignment problem is balanced.
Now let us find the solution.
The cost matrix of the given assignment problem is
Column 3 contains no zero. Go to Step 2.

Thus all the five assignments have been made. The Optimal assignment schedule and total cost is
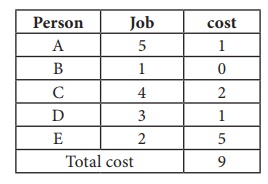
The optimal assignment (minimum) cost = ` 9
Example 10.9
Solve the following assignment problem.
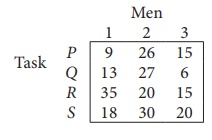
Since the number of columns is less than the number of rows, given assignment problem is unbalanced one. To balance it , introduce a dummy column with all the entries zero. The revised assignment problem is
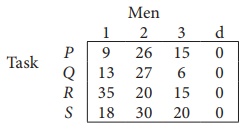
Here only 3 tasks can be assigned to 3 men.
Step 1: is not necessary, since each row contains zero entry. Go to Step 2.
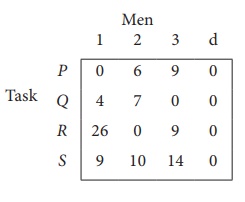
Step 3 (Assignment) :
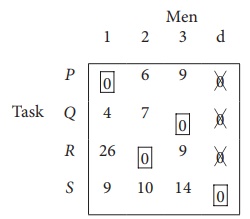
Since each row and each columncontains exactly one assignment,all the three men have been assigned a task. But task S is not assigned to any Man. The optimal assignment schedule and total cost is
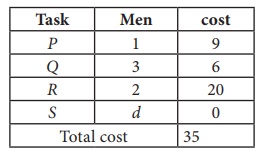
The optimal assignment (minimum) cost = ₹ 35
Related Topics
Privacy Policy , Terms and Conditions , DMCA Policy and Compliant
Copyright © 2018-2023 BrainKart.com; All Rights Reserved. Developed by Therithal info, Chennai.
Principedia

Successful Strategies for Solving Problems on Assignments
Solving complex problems is a challenging task and warrants ongoing effort throughout your career. A number of approaches that expert problem-solvers find useful are summarized below, and you may find these strategies helpful in your own work. Any quantitative problem, whether in economics, science, or engineering, requires a two-step approach: analyze, then compute. Jumping directly to “number-crunching” without thinking through the logic of the problem is counter-productive. Conversely, analyzing a problem and then computing carelessly will not result in the right answer either. So, think first, calculate, and always check your results. And remember, attitude matters. Approach solving a problem as something that you know you can do, rather than something you think that you can’t do. Very few of us can see the answer to a problem without working through various approaches first.
Analysis Stage
- Read the problem carefully at least twice, aloud if possible, then restate the problem in your own words.
- Write down all the information that you know in the problem and separate, if necessary, the “givens” from the “constraints.”
- Think about what can be done with the information that is given. What are some relationships within the information given? What does this particular problem have in common conceptually with course material or other questions that you have solved?
- Draw pictures or graphs to help you sort through what’s really going on in the problem. These will help you recall related course material that will help you solve the problem. However, be sure to check that the assumptions underlying the picture or graph you have drawn are the same as the assumptions made in the problem. If they are not, you will need to take this into consideration when setting up your approach.
Computing Stage
- If the actual numbers involved in the problem are too large, small, or abstract and seem to be getting in the way of your thinking, substitute simple numbers and plan your approach. Then, once you get an understanding of the concepts in the problem, you can go back to the numbers given.
- Once you have a plan, do the necessary calculations. If you think of a simpler or more elegant approach, you can try it afterwards and use it as a check of your logic. Be careful about changing your approach in the middle of a problem. You can inadvertently include some incorrect or inapplicable assumptions from the prior plan.
- Throughout the computing stage, pause periodically to be sure that you understand the intuition behind each concept in the problem. Doing this will not only strengthen your understanding of the material, but it will also help you in solving other problems that also focus on those concepts.
- Resist the temptation to consult the answer key before you have finished the problem. Problems often look logical when someone else does them; that recognition does not require the same knowledge as solving the problem yourself. Likewise, when soliciting help from the AI or course head, ask for direction or a helpful tip only—avoid having them work the problem for you. This approach will help ensure that you really understand the problem—an essential prerequisite for successfully solving problems on exams and quizzes where no outside help is available.
- Check your results. Does the answer make sense given the information you have and the concepts involved? Does the answer make sense in the real world? Are the units reasonable? Are the units the ones specified in the problem? If you substitute your answer for the unknown in the problem, does it fit the criteria given? Does your answer fit within the range of an estimate that you made prior to calculating the result? One especially effective way to check your results is to work with a study partner or group. Discussing various options for a problem can help you uncover both computational errors and errors in your thinking about the problem. Before doing this, of course, make sure that working with someone else is acceptable to your course instructor.
- Ask yourself why this question is important. Lectures, precepts, problem sets, and exams are all intended to increase your knowledge of the subject. Thinking about the connection between a problem and the rest of the course material will strengthen your overall understanding.
If you get stuck, take a break. Research has shown that the brain works very productively on problems while we sleep—so plan your problem-solving sessions in such a way that you do a “first pass.” Then, get a night’s rest, return to the problem set the next day, and think about approaching the problem in an entirely different way.
References and Further Reading:
Adapted in part from Walter Pauk. How to Study in College , 7th edition, Houghton Mifflin Co., 2001
- ← Questions to Ask Yourself When Problem Solving
- Breaking Down Large Projects Into Manageable Pieces →
7 Most Effective Ways For How To Solve Assignment Problems

Here in this blog, CodeAvail experts will explain to you 7 most effective ways for how to solve assignment problems step by step in detail.
How To Solve Assignment Problems
Table of Contents
The most common question asked by many students is how to solve assignment problems. There are many students who are having a hard time with their assignments thats why they are looking for proper guidelines to solve those problems. The assignment is one of the most critical parts of the students’ academic journey, and one always states that I have a lot of assignments to do. Besides this, there is not a single student in the world who has never done any assignment in their academic life. But the students always want to find the best and most effective ways for how to solve assignment problems . In this blog, we have given all the necessary information to help you solve your assignment problems.
How To Solve Assignment Problems-Stepwise Guide
To solve assignment problems, you need to understand the question carefully first. Because if you don’t understand the question, you will not know the information you need to complete your assignments. Follow these steps to know How To Solve assignment Problems :
1) Proper Planning Is Required
This is the first step when you start solving your assignment, you’ll most likely jump directly into the main thing. The primary thing you will do is pull out of your beg, at that point work your way through the remainder of your assignment. There’s a superior way. Know how much time you need to do an assignment. At that point list down all the various chores that you need to do. Check to what extent it will take you to finish every task to check whether you have to permit yourself additional time. Be practical. When your note down everything then the next step is to find the best place for work.
2) Collect All the required Data Before You Start
This is the biggest problem of many students, they don’t really follow this step. Make sure you have all the required information to solve assignment problems. Don’t start your assignment without the proper information. Because after starting your assignment when you come back it may be hard to get once again and write with the same flow. It will just destroy your assignment writing flow. If you have planned efficiently, you should know what exactly you want to complete your assignment and set up everything in your study table you’ll require.
3) Set A Timetable For Certain Assignment
Set a proper timetable to achieve each part of your assignment based on how long you think each part of your assignment will take and how much time you have. Give yourself enough time to complete each part and do other nightly routines. Set a proper time and be honest with it. The less time you waste on checking your laptop or mobile, the more quickly you can complete your assignment. If you believe you can complete everything in a half-hour, set a timer and work honestly to complete it.
4) Stay Away From Distractions
You need a quiet place when you are working on your assignment problems. Problems like Maths assignment problems, Computer science problems needs a quiet place to complete. Keep your telephone away from you, stay away from your PC, and make your surroundings as peaceful as possible. Because to solve assignment problems it requires a lot of focus. Giving work your full focus will really make it simpler, in light of the fact that your brain won’t balance various tasks simultaneously.
Usually, students will attempt to perform multiple tasks, sitting in front of the TV or tuning in to the radio or proceeding to visit on Facebook or Instagram while additionally attempting to do assignments. It will be a lot more enjoyable to do those things after you are done completing your assignment.
5) Taking Breaks is Necessary
If your professor assigns you a lot of assignments to complete, then You want to work straight through hours and hours of assignment if you have a lot to do. But it would probably end up slowing you down and prolonging the whole session.
Get the work done in short periods. Go hard on an assignment, then take a short break to stretch and walk. To keep going, it will re-energize your mind and your body. This strategy will help you solve your assignment problems quickly and help you maintain your assignment’s quality. Try to do your assignment for 1 hour and then take a 10 minutes break.
6) Isolate Yourself
It is one of the best ways to do assignment problems. Because when we isolate ourselves from the outside world, we can do a better concentration on our assignment. The reason is, many outside elements distract our mind from our assignment. When we are going to do our assignment, we should isolate ourselves from our family, social media, and other social activities.
7) Take Help From Online Service Providers
There are many Excel problems that are hard to solve at that time you can take help from online service providers. The reason for taking help from these online service providers because they have years of experience in their respective field. Plus if you need any help you can contact them because they are always available to deal with your problems. They are well aware of the guidelines provided by universities and colleges and know how to solve assignment problems .
Follow all the steps we mentioned above will help in solving your assignment problems. In this article, we have given all the required information that will help you find the answer on how to solve assignment problems . The assignment problems like Maths and Computer science required a lot of focus and proper time management. Time is everything if you manage your time effectively then you will not find any problem solving your assignment problems before the allotted time. Just put away the thing which you think can distract your mind. And give yourself a break after you complete every task because if you give your rain rest then it will be helpful for you to focus on your next task.
If you are facing a problem with completing your assignment or any other assignment, you can take help from us. Our Assignment providers have helped students across the world in completing their assignments on time, get good grades, and at the same time. There’s no doubt that many teachers are handing out assignments that are hard to complete on time. Some assignments can be about an unknown subject. But the truth is, often, the students need assignment help. It is your best decision when you have a lot of tasks to complete but still want to have free time.
As a result, Our computer science assignment help and programming assignment help experts are available for you to 24*7.
Related Posts

How to Hire someone to do my Statistics Homework for Me?
Students ask to do my statistics homework for me. Although there are many online tutors or statistics homework service providing websites available to help you…

How to Get Good Grades in Exams Tips by Experts
Here in this blog, Codeavail professional experts will help you to understand how to get good grades in Exams. Notice that not all the material…
- MATLAB Assignments in Aerodynamics
How to Successfully Handle MATLAB Assignments in Aerodynamics

MATLAB assignments, especially those related to aerodynamics, can seem daunting at first. However, with a structured approach, you can tackle aerodynamics assignment effectively. This blog will help you understand the general steps to solve MATLAB assignments related to aerodynamics, such as the one described above. The focus will be on key concepts, strategies, and MATLAB functions that are commonly used in these types of assignments.
Understanding the Assignment
The first step in solving any MATLAB assignment is to thoroughly understand the problem statement. In the example provided, the goal is to compute the pressure distribution about a symmetric airfoil using a series of sources and sinks. Here's a breakdown of the key tasks involved:
- Generalize the velocity distribution for n sources/sinks.
- Transform the coordinates to place the airfoil in the standard position.
- Compute the pressure coefficient (Cp).
- Generate streamlines and solve for source/sink strengths.
- Compute and analyze the RMS error between the predicted and published pressure distribution.
- Document your results and MATLAB code in a report.

Step-by-Step Approach
1. generalize the velocity distribution.
The velocity distribution for a flow over n sources/sinks is given by:
Here, (xi,yi)(x_i, y_i)(xi,yi) are the locations of the sources/sinks and sis_isi are the source/sink strengths. Implementing this in MATLAB involves creating functions that compute these velocities.
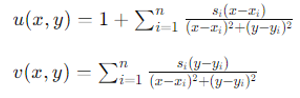
MATLAB Implementation:
2. Transform the Coordinates
To place the airfoil in the standard position, you need to transform the coordinates such that the leading edge is at x=0x = 0x=0 and the trailing edge at x=1x = 1x=1. This is done by placing the sources/sinks as:
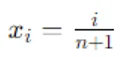
3. Compute the Pressure Coefficient
The pressure coefficient is defined as:
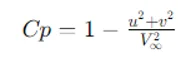
4. Generate Streamlines and Solve for Source/Sink Strengths
Using the stream function ψ(x,y)\psi(x, y)ψ(x,y) and ensuring all airfoil points are on the same streamline (i.e., ψ(Xj,Yj)=0\psi(X_j, Y_j) = 0ψ(Xj,Yj)=0), you can solve for the source/sink strengths.
5. Compute and Analyze the RMS Error
The RMS error helps you compare the predicted and actual pressure distribution:
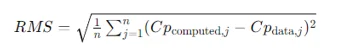
6. Document Your Results
Create a comprehensive report that includes:
- A short introduction
- Plots of the source/sink distribution and pressure coefficients
- Field plots with streamlines, singularity locations, and airfoil points
- RMS error analysis for different numbers of sources
- Your MATLAB code with explanations
Detailed Guide to Solving the Assignment
Let's delve into each step in more detail, focusing on the concepts and practical steps involved.
Generalizing the Velocity Distribution
In aerodynamics, the velocity field around an airfoil can be modeled using a combination of sources and sinks. The goal is to create a mathematical representation that captures the flow characteristics accurately. The equations provided describe the velocity components u(x,y)u(x, y)u(x,y) and v(x,y)v(x, y)v(x,y) in the x and y directions, respectively.
To implement these equations in MATLAB, you need to create a function that computes the velocity at any point (x, y) given the positions and strengths of the sources and sinks. The function iterates through each source/sink, adding their contributions to the overall velocity field.
MATLAB Code Example:
This function initializes the velocity components uuu and vvv, then iteratively updates them based on the contributions from each source/sink.
Transforming the Coordinates
To align the airfoil in the standard position, the sources and sinks need to be placed at specific x-coordinates, defined by xi=in+1x_i = \frac{i}{n + 1}xi=n+1i. This transformation ensures that the leading edge of the airfoil is at x=0x = 0x=0 and the trailing edge is at x=1x = 1x=1.
Computing the Pressure Coefficient
The pressure coefficient CpCpCp is a crucial parameter in aerodynamics, representing the pressure distribution over the airfoil. It is computed using the local velocity components uuu and vvv:
Cp=1−u2+v2V∞2Cp = 1 - \frac{u^2 + v^2}{V_\infty^2}Cp=1−V∞2u2+v2
This equation indicates that CpCpCp is inversely related to the square of the local velocity magnitude. In MATLAB, you can create a function to compute CpCpCp at each point on the airfoil.
Generating Streamlines and Solving for Source/Sink Strengths
Streamlines represent the paths followed by fluid particles in the flow field. In MATLAB, you can use the stream function ψ(x,y)\psi(x, y)ψ(x,y) to generate streamlines. The stream function is related to the velocity components by:
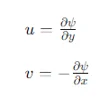
To ensure that all airfoil points lie on the same streamline, you set ψ(Xj,Yj)=0\psi(X_j, Y_j) = 0ψ(Xj,Yj)=0. This creates a system of equations that can be solved for the source/sink strengths sis_isi.
In the solve_source_strengths function, you construct the matrix MMM and the vector RRR to solve for sss.
Computing and Analyzing the RMS Error
The Root Mean Square (RMS) error measures the difference between the computed pressure coefficients and the actual data. This helps evaluate the accuracy of your model.
This function takes the computed and actual CpCpCp values and calculates the RMS error, providing a quantitative measure of the model's accuracy.
Documenting Your Results
A well-documented report is essential for presenting your findings clearly. Your report should include:
- Introduction: Briefly describe the problem and objectives.
- Source/Sink Distribution: Plot and analyze the distribution of sources/sinks.
- Pressure Coefficient: Compare the predicted and actual CpCpCp values.
- Field Plots: Include streamlines, singularity locations, and airfoil points.
- RMS Error Analysis: Present the RMS error for different numbers of sources.
- MATLAB Code: Provide your code with explanations.
Tips for Success
- Understand the Theory: Before diving into MATLAB, make sure you understand the aerodynamic theory and mathematical equations involved.
- Break Down the Problem: Divide the assignment into smaller tasks and tackle them one by one.
- Validate Your Results: Continuously check your results against known solutions or data to ensure accuracy.
- Use Built-In Functions: MATLAB has powerful built-in functions like interp1 for interpolation and ode45 for solving differential equations. Utilize them to simplify your code.
- Document Your Code: Comment your MATLAB code extensively to explain what each part does.
Solving MATLAB assignments in aerodynamics involves a combination of theoretical knowledge and practical programming skills. By following a structured approach and leveraging MATLAB's capabilities, you can efficiently tackle assignments like computing the pressure distribution around an airfoil. Remember, practice and continuous learning are key to solving these assignments effectively.
Post a comment...
Matlab assignments in aerodynamics submit your assignment, attached files.
| File | Actions |
|---|

IMAGES
VIDEO
COMMENTS
The Hungarian method is a computational optimization technique that addresses the assignment problem in polynomial time and foreshadows following primal-dual alternatives. In 1955, Harold Kuhn used the term "Hungarian method" to honour two Hungarian mathematicians, Dénes Kőnig and Jenő Egerváry. Let's go through the steps of the Hungarian method with the help of a solved example.
Solve the assignment problem with ease using the Hungarian method. Our comprehensive guide walks you through the steps to minimize costs and maximize profits.
After reading this article you will learn about:- 1. Meaning of Assignment Problem 2. Definition of Assignment Problem 3. Mathematical Formulation 4. Hungarian Method 5. Variations. Meaning of Assignment Problem: An assignment problem is a particular case of transportation problem where the objective is to assign a number of resources to an equal number of activities so as to minimise total ...
Hungarian algorithm. The Hungarian method is a combinatorial optimization algorithm that solves the assignment problem in polynomial time and which anticipated later primal-dual methods.
The Hungarian algorithm, aka Munkres assignment algorithm, utilizes the following theorem for polynomial runtime complexity ( worst case O (n3)) and guaranteed optimality: If a number is added to or subtracted from all of the entries of any one row or column of a cost matrix, then an optimal assignment for the resulting cost matrix is also an ...
The assignment problem is a fundamental combinatorial optimization problem. In its most general form, the problem is as follows: The problem instance has a number of agents and a number of tasks. Any agent can be assigned to perform any task, incurring some cost that may vary depending on the agent-task assignment.
This problem is known as the assignment problem. The assignment problem is a special case of the transportation problem, which in turn is a special case of the min-cost flow problem, so it can be solved using algorithms that solve the more general cases.
Now we will examine a few highly simplified illustrations of Hungarian Method for solving an assignment problem. Later in the chapter, you will find more practical versions of assignment models like Crew assignment problem, Travelling salesman problem, etc.
Section 7.5: The Assignment ProblemIn this section, we investigate the assignment problem- That is, given n jobs and n people, ssign every job to a unique person. Typically, there are either costs or time involved, and we would want to make the assignments in such. a way as to minimize this quantity.Let's be more speci c with the example from ...
The Hungarian method, also known as the Kuhn-Munkres algorithm, is a computational technique used to solve the assignment problem in polynomial time. It's a precursor to many primal-dual methods used today. The method was named in honor of Hungarian mathematicians Dénes Kőnig and Jenő Egerváry by Harold Kuhn in 1955. Let's delve into the Hungarian method, its steps, and a solved example ...
The assignment problem is one of the special type of transportation problem for which more efficient (less-time consuming) solution method has been devised by KUHN (1956) and FLOOD (1956). The justification of the steps leading to the solution is based on theorems proved by Hungarian mathematicians KONEIG (1950) and EGERVARY (1953), hence the method is named Hungarian.
9. Form a new matrix and repeat step 4 until all assignments have been made. Hungarian method provides a convenient method of solving assignment problems comparative to other available methods. Solution of assignment problems can be classified in five types as shown below.
Of course, real optimization problems have many more than two variables and many constraint functions, making them much harder to solve. The easiest kind of optimization problem to solve is linear, and fortunately, the assignment problem is linear.
The assignment constraints are mathematically defined as: Fehler beim Erstellen des Vorschaubildes: Die Miniaturansicht konnte nicht am vorgesehenen Ort gespeichert werden To make clear how to solve an assignment problem with the Hungarian algorithm we will show you the different cases with several examples which can occur .
The Hungarian algorithm is useful to identify minimum costs when people are assigned to specific activities based on cost. Practice using this algorithm in example equations of real-world scenarios.
This section presents an example that shows how to solve an assignment problem using both the MIP solver and the CP-SAT solver.
The Hungarian algorithm consists of the four steps below. The first two steps are executed once, while Steps 3 and 4 are repeated until an optimal assignment is found. The input of the algorithm is an n by n square matrix with only nonnegative elements.
Step 2: Subtract minimum of every column. 0, 1500 and 0 are subtracted from columns 1, 2 and 3 respectively. 0 0 1000. 500 1000 0. 0 500 500. Step 3: Cover all zeroes with minimum number of horizontal and vertical lines. Step 4: Since we need 3 lines to cover all zeroes, the optimal assignment is found. 2500 4000 3500.
Solve the following assignment problem. Cell values represent cost of assigning job A, B, C and D to the machines I, II, III and IV.
Solving complex problems is a challenging task and warrants ongoing effort throughout your career. A number of approaches that expert problem-solvers find useful are summarized below, and you may find these strategies helpful in your own work. Any quantitative problem, whether in economics, science, or engineering, requires a two-step approach: analyze, then compute. Jumping directly to ...
The assignment problem is particularly interesting because many seemingly different problems may be solved as assignment problems. Moreover, it is an important example of a combinatorial optimization problem; that is, a problem that seeks the best possible arrangement of objects among a specified set of many possible arrangements.
Abstract: Assignment problem is an important problem in mathematics and is also discuss in real physical world. In this paper we attempt to introduce a new proposed approach for solving assignment problem with algorithm and solution steps. We examine a numerical example by using new method and compute by existing two methods.
Students always find the most effective ways for how to solve assignment problems. In this blog, know all the necessary information that you can follow.
The first step in solving any MATLAB assignment is to thoroughly understand the problem statement. In the example provided, the goal is to compute the pressure distribution about a symmetric airfoil using a series of sources and sinks. ... Briefly describe the problem and objectives. ... Break Down the Problem: Divide the assignment into ...
The problem with this neat-sounding conclusion is that it ignores two centuries of well-established practice to the contrary. When a lawsuit involves the protection of rights of the public ...