word problem solving involving quadratic equation

• Pre-Algebra Topics
• Algebra Topics
• Algebra Calculator
• Algebra Cheat Sheet
• Algebra Practice Test
• Algebra Readiness Test
• Algebra Formulas
• Want to Build Your Own Website?

Sign In / Register

Need Help Solving Those Dreaded Word Problems Involving Quadratic Equations?

Yes, I know it's tough. You've finally mastered factoring and using the quadratic formula and now you are asked to solve more problems!

Except these are even more tough. Now you have to figure out what the problem even means before trying to solve it. I completely understand and here's where I am going to try to help!

There are many types of problems that can easily be solved using your knowledge of quadratic equations. You may come across problems that deal with money and predicted incomes (financial) or problems that deal with physics such as projectiles. You may also come across construction type problems that deal with area or geometry problems that deal with right triangles.

Lucky for you, you can solve the quadratic equations, now you just have to learn how to apply this useful skill.

On this particular page, we are going to take a look at a physics "projectile problem".

Projectiles - Example 1

A ball is shot from a cannon into the air with an upward velocity of 40 ft/sec. The equation that gives the height (h) of the ball at any time (t) is: h(t)= -16t 2 + 40ft + 1.5. Find the maximum height attained by the ball.

Let's first take a minute to understand this problem and what it means. We know that a ball is being shot from a cannon. So, in your mind, imagine a cannon firing a ball. We know that the ball is going to shoot from the cannon, go into the air, and then fall to the ground.

So, here's a mathematical picture that I see in my head.

Now let's talk about what each part of this problem means. In our equation that we are given we must be given the value for the force of gravity (coefficient of t 2 ). We must also use our upward velocity (coefficient of t) and our original height of the cannon/ball (the constant or 1.5). Take a look...

Now that you have a mental picture of what's happening and you understand the formula given, we can go ahead and solve the problem.

• First, ask yourself, "What am I solving for?" "What do I need to find?" You are asked to find the maximum height (go back and take a look at the diagram). What part of the parabola is this? Yes, it's the vertex! We will need to use the vertex formula and I will need to know the y coordinate of the vertex because it's asking for the height.
• Next Step: Solve! Now that I know that I need to use the vertex formula, I can get to work.

Just as simple as that, this problem is solved.

Let's not stop here. Let's take this same problem and put a twist on it. There are many other things that we could find out about this ball!

Projectiles - Example 2

Same problem - different question. Take a look...

A ball is shot from a cannon into the air with an upward velocity of 40 ft/sec. The equation that gives the height (h) of the ball at any time (t) is: h(t)= -16t 2 + 40ft + 1.5. How long did it take for the ball to reach the ground?

Now, we've changed the question and we want to know how long did it take the ball to reach the ground.

What ground, you may ask. The problem didn't mention anything about a ground. Let's take a look at the picture "in our mind" again.

Do you see where the ball must fall to the ground. The x-axis is our "ground" in this problem. What do we know about points on the x-axis when we are dealing with quadratic equations and parabolas?

Yes, the points on the x-axis are our "zeros" or x-intercepts. This means that we must solve the quadratic equation in order to find the x-intercept.

Let's do it! Let's solve this equation. I'm thinking that this may not be a factorable equation. Do you agree? So, what's our solution?

Hopefully, you agree that we can use the quadratic formula to solve this equation.

The first time doesn't make sense because it's negative. This is the calculation for when the ball was on the ground initially before it was shot.

This actually never really occurred because the ball was shot from the cannon and was never shot from the ground. Therefore, we will disregard this answer.

The other answer was 2.54 seconds which is when the ball reached the ground (x-axis) after it was shot. Therefore, this is the only correct answer to this problem.

Ok, one more spin on this problem. What would you do in this case?

Projectiles - Example 3

A ball is shot from a cannon into the air with an upward velocity of 40 ft/sec. The equation that gives the height (h) of the ball at any time (t) is: h(t)= -16t 2 + 40ft + 1.5. How long does it take the ball to reach a height of 20 feet?

Yes, this problem is a little trickier because the question is not asking for the maximum height (vertex) or the time it takes to reach the ground (zeros), instead it it asking for the time it takes to reach a height of 20 feet.

Since the ball reaches a maximum height of 26.5 ft, we know that it will reach a height of 20 feet on the way up and on the way down.

Let's just estimate on our graph and also make sure that we get this visual in our head.

From looking at this graph, I would estimate the times to be about 0.7 sec and 1.9 sec. Do you see how the ball will reach 20 feet on the way up and on the way down?

Now, let's find the actual values. Where will we substitute 20 feet?

Yes, we must substitute 20 feet for h(t) because this is the given height. We will now be solving for t using the quadratic formula. Take a look.

Our actual times were pretty close to our estimates. Just don't forget that when you solve a quadratic equation, you must have the equation set equal to 0. Therefore, we had to subtract 20 from both sides in order to have the equation set to 0.

You've now seen it all when it comes to projectiles!

Great Job! Hopefully you've been able to understand how to solve problems involving quadratic equations. I also hope that you better understand these common velocity equations and how to think about what this problem looks like graphically in order to help you to understand which process or formula to use in order to solve the problem.

• Quadratic Equations
• Projectile Problems

Need More Help With Your Algebra Studies?

Get access to hundreds of video examples and practice problems with your subscription! 

Click here for more information on our affordable subscription options.

Not ready to subscribe?  Register for our FREE Pre-Algebra Refresher course.

ALGEBRA CLASS E-COURSE MEMBERS

Click here for more information on our Algebra Class e-courses.

Need Help? Try This Online Calculator!

Affiliate Products...

On this site, I recommend only one product that I use and love and that is Mathway   If you make a purchase on this site, I may receive a small commission at no cost to you. 

Privacy Policy

Let Us Know How we are doing!

  send us a message to give us more detail!

Would you prefer to share this page with others by linking to it?

• Click on the HTML link code below.
• Copy and paste it, adding a note of your own, into your blog, a Web page, forums, a blog comment, your Facebook account, or anywhere that someone would find this page valuable.

Copyright © 2009-2020   |   Karin Hutchinson   |   ALL RIGHTS RESERVED.

Quadratic Equations Word Problems

These lessons, with videos, examples, and step-by-step solutions, help Algebra 1 students learn to solve geometry word problems using quadratic equations.

Related Pages Solving Quadratic Equations by Factoring Solving Quadratic Equations by Completing the Square More Lessons for Grade 9 Math Worksheets

Quadratic equations - Solving word problems using factoring of trinomials Question 1a: Find two consecutive integers that have a product of 42

Quadratic equations - Solving word problems using factoring of trinomials Question 1b: There are three consecutive integers. The product of the two larger integers is 30. Find the three integers.

Quadratic Equations - Solving Word problems by Factoring Question 1c: A rectangular building is to be placed on a lot that measures 30 m by 40 m. The building must be placed in the lot so that the width of the lawn is the same on all four sides of the building. Local restrictions state that the building cannot occupy any more than 50% of the property. What are the dimensions of the largest building that can be built on the property?

More Word Problems Using Quadratic Equations Example 1 Suppose the area of a rectangle is 114.4 m 2 and the length is 14 m longer than the width. Find the length and width of the rectangle.

More Word Problems Using Quadratic Equations Example 2 A manufacturer develops a formula to determine the demand for its product depending on the price in dollars. The formula is D = 2,000 + 100P - 6P 2 where P is the price per unit, and D is the number of units in demand. At what price will the demand drop to 1000 units?

More Word Problems Using Quadratic Equations Example 3 The length of a car’s skid mark in feet as a function of the car’s speed in miles per hour is given by l(s) = .046s 2 - .199s + 0.264 If the length of skid mark is 220 ft, find the speed in miles per hour the car was traveling.

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.

• Parallelogram
• Quadrilateral
• Parallelepiped
• Tetrahedron
• Dodecahedron
• Fraction Calculator
• Mixed Fraction Calculator
• Greatest Common Factor Calulator
• Decimal to Fraction Calculator
• Whole Numbers
• Rational Numbers
• Place Value
• Irrational Numbers
• Natural Numbers
• Binary Operation
• Numerator and Denominator
• Order of Operations (PEMDAS)
• Scientific Notation

Last modified on August 3rd, 2023

Quadratic Equation Word Problems

Here, we will solve different types of quadratic equation-based word problems. Use the appropriate method to solve them:

• By Completing the Square
• By Factoring
• By Quadratic Formula
• By graphing

For each process, follow the following typical steps:

• Make the equation
• Solve for the unknown variable using the appropriate method
• Interpret the result

The product of two consecutive integers is 462. Find the numbers?

Let the numbers be x and x + 1 According to the problem, x(x + 1) = 483 => x 2 + x – 483 = 0 => x 2 + 22x – 21x – 483 = 0 => x(x + 22) – 21(x + 22) = 0 => (x + 22)(x – 21) = 0 => x + 22 = 0 or x – 21 = 0 => x = {-22, 21} Thus, the two consecutive numbers are 21 and 22.

The product of two consecutive positive odd integers is 1 less than four times their sum. What are the two positive integers.

Let the numbers be n and n + 2 According to the problem, => n(n + 2) = 4[n + (n + 2)] – 1 => n 2 + 2n = 4[2n + 2] – 1 => n 2 + 2n = 8n + 7 => n 2 – 6n – 7 = 0 => n 2 -7n + n – 7 = 0 => n(n – 7) + 1(n – 7) = 0 => (n – 7) (n – 1) = 0 => n – 7 = 0 or n – 1 = 0 => n = {7, 1} If n = 7, then n + 2 = 9 If n = 1, then n + 1 = 2 Since 1 and 2 are not possible. The two numbers are 7 and 9

A projectile is launched vertically upwards with an initial velocity of 64 ft/s from a height of 96 feet tower. If height after t seconds is reprented by h(t) = -16t 2 + 64t + 96. Find the maximum height the projectile reaches. Also, find the time it takes to reach the highest point.

Since the graph of the given function is a parabola, it opens downward because the leading coefficient is negative. Thus, to get the maximum height, we have to find the vertex of this parabola. Given the function is in the standard form h(t) = a 2 x + bx + c, the formula to calculate the vertex is: Vertex (h, k) = ${\left\{ \left( \dfrac{-b}{2a}\right) ,h\left( -\dfrac{b}{2a}\right) \right\}}$ => ${\dfrac{-b}{2a}=\dfrac{-64}{2\times \left( -16\right) }}$ = 2 seconds Thus, the time the projectile takes to reach the highest point is 2 seconds ${h\left( \dfrac{-b}{2a}\right)}$ = h(2) = -16(2) 2 – 64(2) + 80 = 144 feet Thus, the maximum height the projectile reaches is 144 feet

The difference between the squares of two consecutive even integers is 68. Find the numbers.

Let the numbers be x and x + 2 According to the problem, (x + 2) 2 – x 2 = 68 => x 2 + 4x + 4 – x 2 = 68 => 4x + 4 = 68 => 4x = 68 – 4 => 4x = 64 => x = 16 Thus the two numbers are 16 and 18

The length of a rectangle is 5 units more than twice the number. The width is 4 unit less than the same number. Given the area of the rectangle is 15 sq. units, find the length and breadth of the rectangle.

Let the number be x Thus, Length = 2x + 5 Breadth = x – 4 According to the problem, (2x + 5)(x – 4) = 15 => 2x 2 – 8x + 5x – 20 – 15 = 0 => 2x 2 – 3x – 35 = 0 => 2x 2 – 10x + 7x – 35 = 0 => 2x(x – 5) + 7(x – 5) = 0 => (x – 5)(2x + 7) = 0 => x – 5 = 0 or 2x + 7 = 0 => x = {5, -7/2} Since we cannot have a negative measurement in mensuration, the number is 5 inches. Now, Length = 2x + 5 = 2(5) + 5 = 15 inches Breadth = x – 4 = 15 – 4 = 11 inches

A rectangular garden is 50 cm long and 34 cm wide, surrounded by a uniform boundary. Find the width of the boundary if the total area is 540 cm².

Given, Length of the garden = 50 cm Width of the garden = 34 cm Let the uniform width of the boundary be = x cm According to the problem, (50 + 2x)(34 + 2x) – 50 × 34 = 540 => 4x 2 + 168x – 540 = 0 => x 2 + 42x – 135 = 0 Since, this quadratic equation is in the standard form ax 2 + bx + c, we will use the quadratic formula, here a = 1, b = 42, c = -135 x = ${x=\dfrac{-b\pm \sqrt{b^{2}-4ac}}{2a}}$ => ${\dfrac{-42\pm \sqrt{\left( 42\right) ^{2}-4\times 1\times \left( -135\right) }}{2\times 1}}$ => ${\dfrac{-42\pm \sqrt{1764+540}}{2}}$ => ${\dfrac{-42\pm \sqrt{2304}}{2}}$ => ${\dfrac{-42\pm 48}{2}}$ => ${\dfrac{-42+48}{2}}$ and ${\dfrac{-42-48}{2}}$ => x = {-45, 3} Since we cannot have a negative measurement in mensuration the width of the boundary is 3 cm

The hypotenuse of a right-angled triangle is 20 cm. The difference between its other two sides is 4 cm. Find the length of the sides.

Let the length of the other two sides be x and x + 4 According to the problem, (x + 4) 2 + x 2 = 20 2 => x 2 + 8x + 16 + x 2 = 400 => 2x 2 + 8x + 16 = 400 => 2x 2 + 8x – 384 = 0 => x 2 + 4x – 192 = 0 => x 2 + 16x – 12x – 192 = 0 => x(x + 16) – 12(x + 16) = 0 => (x + 16)(x – 12) = 0 => x + 16 = 0 and x – 12 = 0 => x = {-16, 12} Since we cannot have a negative measurement in mensuration, the lengths of the sides are 12 and 16

Jennifer jumped off a cliff into the swimming pool. The function h can express her height as a function of time (t) = -16t 2 +16t + 480, where t is the time in seconds and h is the height in feet. a) How long did it take for Jennifer to attain a maximum length. b) What was the highest point that Jennifer reached. c) Calculate the time when Jennifer hit the water?

Comparing the given function with the given function f(x) = ax 2 + bx + c, here a = -16, b = 16, c = 480 a) Finding the vertex will give us the time taken by Jennifer to reach her maximum height  x = ${-\dfrac{b}{2a}}$ = ${\dfrac{-16}{2\left( -16\right) }}$ = 0.5 seconds Thus Jennifer took 0.5 seconds to reach her maximum height b) Putting the value of the vertex by substitution in the function, we get ${h\left( \dfrac{1}{2}\right) =-16\left( \dfrac{1}{2}\right) ^{2}+16\left( \dfrac{1}{2}\right) +480}$ => ${-16\left( \dfrac{1}{4}\right) +8+480}$ => 484 feet Thus the highest point that Jennifer reached was 484 feet c) When Jennifer hit the water, her height was 0 Thus, by substituting the value of the height in the function, we get -16t 2 +16t + 480 = 0 => -16(t 2 + t – 30) = 0 => t 2 + t – 30 = 0 => t 2 + 6t – 5t – 30 = 0 => t(t + 6) – 5(t + 6) = 0 => (t + 6)(t – 5) = 0 => t + 6 = 0 or t – 5 = 0 => x = {-6, 5} Since time cannot have any negative value, the time taken by Jennifer to hit the water is 5 seconds.

Leave a Reply Cancel reply

Your email address will not be published. Required fields are marked *

Save my name, email, and website in this browser for the next time I comment.

About us Contact us

• Trigonometry

Join Our Newsletter

© 2024 Mathmonks.com . All rights reserved. Reproduction in whole or in part without permission is prohibited.

Quadradic Equation Word Problems - Examples & Practice - Expii

Quadradic equation word problems - examples & practice, explanations (3), quadratic word problems.

Let's look at 2 pretty common types of word problems that use quadratic functions. Recall that quadratic expressions follow this general form: y=ax2+bx+c In a quadratic expression, a and b are coefficients (numbers in front of the variable x), and c is constant (a number by itself). It's important to remember that a≠0 . It's possible for b=0 and/or c=0, but they don't have to.

Example 1: Word problems involving area

Many quadratic word problems use the area of a rectangle. Here is a graphic to get you started

Image source: By Caroline Kulczycky

Here is another example.

Singh knows the total area of his garden is 50 m2, but he doesn't know the length or width. Use the diagram below to find the length and width in meters (m).

Recall that the formula for area of a rectangle is length⋅width. So, let's plug the values from Singh's garden into that formula, and set it equal to 50 (the area). area=length⋅width50=x⋅(x−5)

Now, let's multiply out this equation and get it in the standard quadratic form (written at the top of this explanation):

Once we multiply the equation out and rearrange it, what does it look like (in quadratic form)?

−x2−5x−50=0

−x2−5x+50=0

Related Lessons

(videos) solving geometry word problems using quadratic equations.

by PatrickJMT

This video by Patrick JMT covers a quadratic word problem based on area of a rectangle.

Patrick walks us through how to solve the following quadratic geometry problem:

“A picture inside a frame is 2 inches longer than it is wide. The picture is in a frame that has width 3 inches on each side of the picture. If the area of the pic, including the frame is 195 in.2, find the dimensions of the frame.”

He goes on to explain how we get the equations for the sides of the frame, so the whole problem looks like:

We know the area of the picture frame, 195 in2. We can set the two sides of the frame equal to that and find a value for x.

(x+6)(x+8)=195

Using the FOIL method , we get an equation that looks like

x2+14x+48=195

We want the left side to equal 0, so subtracting 195 from both sides will give us

x2+14x–147=0

This looks pretty hard to factor. Let’s use our handy dandy quadratic formula .

Our values are going to be a=1,b=14, and c=−147

x=−b±√b2−4ac2ax=−14±√142–4(1)(−147)2(1)x=−14±√196+5882x=−14±√7842x=−14±282x=−7±14

*Note: be careful with the square root!

This leaves us two values for x, x=7 or x=−21. We cannot have a negative measurement, so our final answer is x=7.

(Videos) Solve Projectile Problems Using Quadratics

This video by Patrick JMT works through a word problem based on projectile motion .

Solving a Projectile Problem Using Quadratics

Patrick uses the following problem as an example of projectile motion:

“Larry throws a rock in the air. The height, h, in feet above the ground of the rock is given by: h=−16t2+123t+40. How long is the rock in the air?”

From this equation, at time t=0, we gather that h=40. This means Larry is on a cliff with height 40. We want to know the time at which the rock reaches a height of 0. So, plugging in 0 for h, we get an equation:

0=−16t2+123t+40

This is now a quadratic equation, which we can solve for using the quadratic formula! We have values of a=16,b=123, and c=40. We can plug these into the quadratic formula: t=−b±√b2−4ac2at=−123±√(123)2−4(−16)(40)2(−16)t=−123±√17689−32t=123±√1768932t=123±13332t=8,−516

We get two solutions: 8 and −516. t is time, which can't be negative, so our answer is t=8.

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons
• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

9.6: Solve Applications of Quadratic Equations

• Last updated
• Save as PDF
• Page ID 5177

Learning Objectives

By the end of this section, you will be able to:

• Solve applications modeled by quadratic equations

Before you get started, take this readiness quiz.

• The sum of two consecutive odd numbers is \(−100\). Find the numbers. If you missed this problem, review Example 2.18.
• Solve: \(\frac{2}{x+1}+\frac{1}{x-1}=\frac{1}{x^{2}-1}\). If you missed this problem, review Example 7.35.
• Find the length of the hypotenuse of a right triangle with legs \(5\) inches and \(12\) inches. If you missed this problem, review Example 2.34.

Solve Applications Modeled by Quadratic Equations

We solved some applications that are modeled by quadratic equations earlier, when the only method we had to solve them was factoring. Now that we have more methods to solve quadratic equations, we will take another look at applications.

Let’s first summarize the methods we now have to solve quadratic equations.

Methods to Solve Quadratic Equations

• Square Root Property
• Completing the Square
• Quadratic Formula

As you solve each equation, choose the method that is most convenient for you to work the problem. As a reminder, we will copy our usual Problem-Solving Strategy here so we can follow the steps.

Use a Problem-Solving Strategy

• Read the problem. Make sure all the words and ideas are understood.
• Identify what we are looking for.
• Name what we are looking for. Choose a variable to represent that quantity.
• Translate into an equation. It may be helpful to restate the problem in one sentence with all the important information. Then, translate the English sentence into an algebraic equation.
• Solve the equation using algebra techniques.
• Check the answer in the problem and make sure it makes sense.
• Answer the question with a complete sentence.

We have solved number applications that involved consecutive even and odd integers, by modeling the situation with linear equations. Remember, we noticed each even integer is \(2\) more than the number preceding it. If we call the first one \(n\), then the next one is \(n+2\). The next one would be \(n+2+2\) or \(n+4\). This is also true when we use odd integers. One set of even integers and one set of odd integers are shown below.

\(\begin{array}{cl}{}&{\text{Consecutive even integers}}\\{}& {64,66,68}\\ {n} & {1^{\text { st }} \text { even integer }} \\ {n+2} & {2^{\text { nd }} \text { consecutive even integer }} \\ {n+4} & {3^{\text { rd }} \text { consecutive even integer }}\end{array}\)

\(\begin{array}{cl}{}&{\text{Consecutive odd integers}}\\{}& {77,79,81}\\ {n} & {1^{\text { st }} \text { odd integer }} \\ {n+2} & {2^{\text { nd }} \text { consecutive odd integer }} \\ {n+4} & {3^{\text { rd }} \text { consecutive odd integer }}\end{array}\)

Some applications of odd or even consecutive integers are modeled by quadratic equations. The notation above will be helpful as you name the variables.

Example \(\PageIndex{1}\)

The product of two consecutive odd integers is \(195\). Find the integers.

Step 1 : Read the problem

Step 2 : Identify what we are looking for.

We are looking for two consecutive odd integers.

Step 3 : Name what we are looking for.

Let \(n=\) the first odd integer.

\(n+2=\) the next odd integer.

Step 4 : Translate into an equation. State the problem in one sentence.

“The product of two consecutive odd integers is \(195\).” The product of the first odd integer and the second odd integer is \(195\).

Translate into an equation.

\(n(n+2)=195\)

Step 5 : Solve the equation. Distribute.

\(n^{2}+2 n=195\)

Write the equation in standard form.

\(n^{2}+2 n-195=0\)

\((n+15)(n-13)=0\)

Use the Zero Product Property.

\(n+15=0 \quad n-13=0\)

Solve each equation.

\(n=-15, \quad n=13\)

There are two values of \(n\) that are solutions. This will give us two pairs of consecutive odd integers for our solution.

\(\begin{array}{cc}{\text { First odd integer } n=13} & {\text { First odd integer } n=-15} \\ {\text { next odd integer } n+2} & {\text { next odd integer } n+2} \\ {13+2} & {-15+2} \\ {15} & {-13}\end{array}\)

Step 6 : Check the answer.

Do these pairs work? Are they consecutive odd integers?

\(\begin{aligned} 13,15 & \text { yes } \\-13,-15 & \text { yes } \end{aligned}\)

Is their product \(195\)?

\(\begin{aligned} 13 \cdot 15 &=195 &\text{yes} \\-13(-15) &=195 & \text { yes } \end{aligned}\)

Step 7 : Answer the question.

Two consecutive odd integers whose product is \(195\) are \(13,15\) and \(-13,-15\).

Exercise \(\PageIndex{1}\)

The product of two consecutive odd integers is \(99\). Find the integers.

The two consecutive odd integers whose product is \(99\) are \(9, 11\), and \(−9, −11\).

Exercise \(\PageIndex{2}\)

The product of two consecutive even integers is \(168\). Find the integers.

The two consecutive even integers whose product is \(128\) are \(12, 14\) and \(−12, −14\).

We will use the formula for the area of a triangle to solve the next example.

Definition \(\PageIndex{1}\)

Area of a Triangle

For a triangle with base, \(b\), and height, \(h\), the area, \(A\), is given by the formula \(A=\frac{1}{2} b h\).

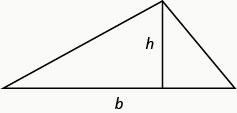
Recall that when we solve geometric applications, it is helpful to draw the figure.

Example \(\PageIndex{2}\)

An architect is designing the entryway of a restaurant. She wants to put a triangular window above the doorway. Due to energy restrictions, the window can only have an area of \(120\) square feet and the architect wants the base to be \(4\) feet more than twice the height. Find the base and height of the window.

Exercise \(\PageIndex{3}\)

Find the base and height of a triangle whose base is four inches more than six times its height and has an area of \(456\) square inches.

The height of the triangle is \(12\) inches and the base is \(76\) inches.

Exercise \(\PageIndex{4}\)

If a triangle that has an area of \(110\) square feet has a base that is two feet less than twice the height, what is the length of its base and height?

The height of the triangle is \(11\) feet and the base is \(20\) feet.

In the two preceding examples, the number in the radical in the Quadratic Formula was a perfect square and so the solutions were rational numbers. If we get an irrational number as a solution to an application problem, we will use a calculator to get an approximate value.

We will use the formula for the area of a rectangle to solve the next example.

Definition \(\PageIndex{2}\)

Area of a Rectangle

For a rectangle with length, \(L\), and width, \(W\), the area, \(A\), is given by the formula \(A=LW\).

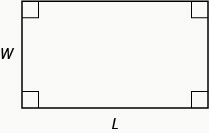
Example \(\PageIndex{3}\)

Mike wants to put \(150\) square feet of artificial turf in his front yard. This is the maximum area of artificial turf allowed by his homeowners association. He wants to have a rectangular area of turf with length one foot less than \(3\) times the width. Find the length and width. Round to the nearest tenth of a foot.

Exercise \(\PageIndex{5}\)

The length of a \(200\) square foot rectangular vegetable garden is four feet less than twice the width. Find the length and width of the garden, to the nearest tenth of a foot.

The length of the garden is approximately \(18\) feet and the width \(11\) feet.

Exercise \(\PageIndex{6}\)

A rectangular tablecloth has an area of \(80\) square feet. The width is \(5\) feet shorter than the length.What are the length and width of the tablecloth to the nearest tenth of a foot?

The length of the tablecloth is approximately \(11.8\) feet and the width \(6.8\) feet.

The Pythagorean Theorem gives the relation between the legs and hypotenuse of a right triangle. We will use the Pythagorean Theorem to solve the next example.

Definition \(\PageIndex{3}\)

Pythagorean Theorem

• In any right triangle, where \(a\) and \(b\) are the lengths of the legs, and \(c\) is the length of the hypotenuse, \(a^{2}+b^{2}=c^{2}\).

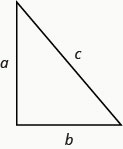
Example \(\PageIndex{4}\)

Rene is setting up a holiday light display. He wants to make a ‘tree’ in the shape of two right triangles, as shown below, and has two \(10\)-foot strings of lights to use for the sides. He will attach the lights to the top of a pole and to two stakes on the ground. He wants the height of the pole to be the same as the distance from the base of the pole to each stake. How tall should the pole be?

Exercise \(\PageIndex{7}\)

The sun casts a shadow from a flag pole. The height of the flag pole is three times the length of its shadow. The distance between the end of the shadow and the top of the flag pole is \(20\) feet. Find the length of the shadow and the length of the flag pole. Round to the nearest tenth.

The length of the flag pole’s shadow is approximately \(6.3\) feet and the height of the flag pole is \(18.9\) feet.

Exercise \(\PageIndex{8}\)

The distance between opposite corners of a rectangular field is four more than the width of the field. The length of the field is twice its width. Find the distance between the opposite corners. Round to the nearest tenth.

The distance between the opposite corners is approximately \(7.2\) feet.

The height of a projectile shot upward from the ground is modeled by a quadratic equation. The initial velocity, \(v_{0}\), propels the object up until gravity causes the object to fall back down.

Definition \(\PageIndex{4}\)

The height in feet, \(h\), of an object shot upwards into the air with initial velocity, \(v_{0}\), after \(t\) seconds is given by the formula

\(h=-16 t^{2}+v_{0} t\)

We can use this formula to find how many seconds it will take for a firework to reach a specific height.

Example \(\PageIndex{5}\)

A firework is shot upwards with initial velocity \(130\) feet per second. How many seconds will it take to reach a height of \(260\) feet? Round to the nearest tenth of a second.

Exercise \(\PageIndex{9}\)

An arrow is shot from the ground into the air at an initial speed of \(108\) ft/s. Use the formula \(h=-16 t^{2}+v_{0} t\) to determine when the arrow will be \(180\) feet from the ground. Round the nearest tenth.

The arrow will reach \(180\) feet on its way up after \(3\) seconds and again on its way down after approximately \(3.8\) seconds.

Exercise \(\PageIndex{10}\)

A man throws a ball into the air with a velocity of \(96\) ft/s. Use the formula \(h=-16 t^{2}+v_{0} t\) to determine when the height of the ball will be \(48\) feet. Round to the nearest tenth.

The ball will reach \(48\) feet on its way up after approximately \(.6\) second and again on its way down after approximately \(5.4\) seconds.

We have solved uniform motion problems using the formula \(D=rt\) in previous chapters. We used a table like the one below to organize the information and lead us to the equation.

The formula \(D=rt\) assumes we know \(r\) and \(t\) and use them to find \(D\). If we know \(D\) and \(r\) and need to find \(t\), we would solve the equation for \(t\) and get the formula \(t=\frac{D}{r}\).

Some uniform motion problems are also modeled by quadratic equations.

Example \(\PageIndex{6}\)

Professor Smith just returned from a conference that was \(2,000\) miles east of his home. His total time in the airplane for the round trip was \(9\) hours. If the plane was flying at a rate of \(450\) miles per hour, what was the speed of the jet stream?

This is a uniform motion situation. A diagram will help us visualize the situation.

We fill in the chart to organize the information.

We are looking for the speed of the jet stream. Let \(r=\) the speed of the jet stream.

When the plane flies with the wind, the wind increases its speed and so the rate is \(450 + r\).

When the plane flies against the wind, the wind decreases its speed and the rate is \(450 − r\).

The speed of the jet stream was \(50\) mph.

Exercise \(\PageIndex{11}\)

MaryAnne just returned from a visit with her grandchildren back east. The trip was \(2400\) miles from her home and her total time in the airplane for the round trip was \(10\) hours. If the plane was flying at a rate of \(500\) miles per hour, what was the speed of the jet stream?

The speed of the jet stream was \(100\) mph.

Exercise \(\PageIndex{12}\)

Gerry just returned from a cross country trip. The trip was \(3000\) miles from his home and his total time in the airplane for the round trip was \(11\) hours. If the plane was flying at a rate of \(550\) miles per hour, what was the speed of the jet stream?

Work applications can also be modeled by quadratic equations. We will set them up using the same methods we used when we solved them with rational equations.We’ll use a similar scenario now.

Example \(\PageIndex{7}\)

The weekly gossip magazine has a big story about the presidential election and the editor wants the magazine to be printed as soon as possible. She has asked the printer to run an extra printing press to get the printing done more quickly. Press #1 takes \(12\) hours more than Press #2 to do the job and when both presses are running they can print the job in \(8\) hours. How long does it take for each press to print the job alone?

This is a work problem. A chart will help us organize the information.

We are looking for how many hours it would take each press separately to complete the job.

Exercise \(\PageIndex{13}\)

The weekly news magazine has a big story naming the Person of the Year and the editor wants the magazine to be printed as soon as possible. She has asked the printer to run an extra printing press to get the printing done more quickly. Press #1 takes \(6\) hours more than Press #2 to do the job and when both presses are running they can print the job in \(4\) hours. How long does it take for each press to print the job alone?

Press #1 would take \(12\) hours, and Press #2 would take \(6\) hours to do the job alone.

Exercise \(\PageIndex{14}\)

Erlinda is having a party and wants to fill her hot tub. If she only uses the red hose it takes \(3\) hours more than if she only uses the green hose. If she uses both hoses together, the hot tub fills in \(2\) hours. How long does it take for each hose to fill the hot tub?

The red hose take \(6\) hours and the green hose take \(3\) hours alone.

Access these online resources for additional instruction and practice with solving applications modeled by quadratic equations.

• Word Problems Involving Quadratic Equations
• Quadratic Equation Word Problems
• Applying the Quadratic Formula

Key Concepts

• Translate into an equation. It may be helpful to restate the problem in one sentence with all the important information. Then, translate the English sentence into an algebra equation.
• Solve the equation using good algebra techniques.
• For a triangle with base, \(b\), and height, \(h\), the area, \(A\), is given by the formula \(A=\frac{1}{2}bh\).

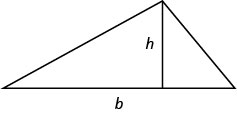
• For a rectangle with length,\(L\), and width, \(W\), the area, \(A\), is given by the formula \(A=LW\).

• The height in feet, \(h\), of an object shot upwards into the air with initial velocity, \(v_{0}\), after \(t\) seconds is given by the formula \(h=-16 t^{2}+v_{0} t\).

Want to create or adapt books like this? Learn more about how Pressbooks supports open publishing practices.

Chapter 10: Quadratics

10.7 Quadratic Word Problems: Age and Numbers

Quadratic-based word problems are the third type of word problems covered in MATQ 1099, with the first being linear equations of one variable and the second linear equations of two or more variables. Quadratic equations can be used in the same types of word problems as you encountered before, except that, in working through the given data, you will end up constructing a quadratic equation. To find the solution, you will be required to either factor the quadratic equation or use substitution.

Example 10.7.1

The sum of two numbers is 18, and the product of these two numbers is 56. What are the numbers?

First, we know two things:

[latex]\begin{array}{l} \text{smaller }(S)+\text{larger }(L)=18\Rightarrow L=18-S \\ \\ S\times L=56 \end{array}[/latex]

Substituting [latex]18-S[/latex] for [latex]L[/latex] in the second equation gives:

[latex]S(18-S)=56[/latex]

Multiplying this out gives:

[latex]18S-S^2=56[/latex]

Which rearranges to:

[latex]S^2-18S+56=0[/latex]

Second, factor this quadratic to get our solution:

[latex]\begin{array}{rrrrrrl} S^2&-&18S&+&56&=&0 \\ (S&-&4)(S&-&14)&=&0 \\ \\ &&&&S&=&4, 14 \end{array}[/latex]

[latex]\begin{array}{l} S=4, L=18-4=14 \\ \\ S=14, L=18-14=4 \text{ (this solution is rejected)} \end{array}[/latex]

Example 10.7.2

The difference of the squares of two consecutive even integers is 68. What are these numbers?

The variables used for two consecutive integers (either odd or even) is [latex]x[/latex] and [latex]x + 2[/latex]. The equation to use for this problem is [latex](x + 2)^2 - (x)^2 = 68[/latex]. Simplifying this yields:

[latex]\begin{array}{rrrrrrrrr} &&(x&+&2)^2&-&(x)^2&=&68 \\ x^2&+&4x&+&4&-&x^2&=&68 \\ &&&&4x&+&4&=&68 \\ &&&&&-&4&&-4 \\ \hline &&&&&&\dfrac{4x}{4}&=&\dfrac{64}{4} \\ \\ &&&&&&x&=&16 \end{array}[/latex]

This means that the two integers are 16 and 18.

Example 10.7.3

The product of the ages of Sally and Joey now is 175 more than the product of their ages 5 years prior. If Sally is 20 years older than Joey, what are their current ages?

The equations are:

[latex]\begin{array}{rrl} (S)(J)&=&175+(S-5)(J-5) \\ S&=&J+20 \end{array}[/latex]

Substituting for S gives us:

[latex]\begin{array}{rrrrrrrrcrr} (J&+&20)(J)&=&175&+&(J&+&20-5)(J&-&5) \\ J^2&+&20J&=&175&+&(J&+&15)(J&-&5) \\ J^2&+&20J&=&175&+&J^2&+&10J&-&75 \\ -J^2&-&10J&&&-&J^2&-&10J&& \\ \hline &&\dfrac{10J}{10}&=&\dfrac{100}{10} &&&&&& \\ \\ &&J&=&10 &&&&&& \end{array}[/latex]

This means that Joey is 10 years old and Sally is 30 years old.

For Questions 1 to 12, write and solve the equation describing the relationship.

• The sum of two numbers is 22, and the product of these two numbers is 120. What are the numbers?
• The difference of two numbers is 4, and the product of these two numbers is 140. What are the numbers?
• The difference of two numbers is 8, and the sum of the squares of these two numbers are 320. What are the numbers?
• The sum of the squares of two consecutive even integers is 244. What are these numbers?
• The difference of the squares of two consecutive even integers is 60. What are these numbers?
• The sum of the squares of two consecutive even integers is 452. What are these numbers?
• Find three consecutive even integers such that the product of the first two is 38 more than the third integer.
• Find three consecutive odd integers such that the product of the first two is 52 more than the third integer.
• The product of the ages of Alan and Terry is 80 more than the product of their ages 4 years prior. If Alan is 4 years older than Terry, what are their current ages?
• The product of the ages of Cally and Katy is 130 less than the product of their ages in 5 years. If Cally is 3 years older than Katy, what are their current ages?
• The product of the ages of James and Susan in 5 years is 230 more than the product of their ages today. What are their ages if James is one year older than Susan?
• The product of the ages (in days) of two newborn babies Simran and Jessie in two days will be 48 more than the product of their ages today. How old are the babies if Jessie is 2 days older than Simran?

Example 10.7.4

Doug went to a conference in a city 120 km away. On the way back, due to road construction, he had to drive 10 km/h slower, which resulted in the return trip taking 2 hours longer. How fast did he drive on the way to the conference?

The first equation is [latex]r(t) = 120[/latex], which means that [latex]r = \dfrac{120}{t}[/latex] or [latex]t = \dfrac{120}{r}[/latex].

For the second equation, [latex]r[/latex] is 10 km/h slower and [latex]t[/latex] is 2 hours longer. This means the second equation is [latex](r - 10)(t + 2) = 120[/latex].

We will eliminate the variable [latex]t[/latex] in the second equation by substitution:

[latex](r-10)(\dfrac{120}{r}+2)=120[/latex]

Multiply both sides by [latex]r[/latex] to eliminate the fraction, which leaves us with:

[latex](r-10)(120+2r)=120r[/latex]

Multiplying everything out gives us:

[latex]\begin{array}{rrrrrrrrr} 120r&+&2r^2&-&1200&-&20r&=&120r \\ &&2r^2&+&100r&-&1200&=&120r \\ &&&-&120r&&&&-120r \\ \hline &&2r^2&-&20r&-&1200&=&0 \end{array}[/latex]

This equation can be reduced by a common factor of 2, which leaves us with:

[latex]\begin{array}{rrl} r^2-10r-600&=&0 \\ (r-30)(r+20)&=&0 \\ r&=&30\text{ km/h or }-20\text{ km/h (reject)} \end{array}[/latex]

Example 10.7.5

Mark rows downstream for 30 km, then turns around and returns to his original location. The total trip took 8 hr. If the current flows at 2 km/h, how fast would Mark row in still water?

If we let [latex]t =[/latex] the time to row downstream, then the time to return is [latex]8\text{ h}- t[/latex].

The first equation is [latex](r + 2)t = 30[/latex]. The stream speeds up the boat, which means [latex]t = \dfrac{30}{(r + 2)}[/latex], and the second equation is [latex](r - 2)(8 - t) = 30[/latex] when the stream slows down the boat.

We will eliminate the variable [latex]t[/latex] in the second equation by substituting [latex]t=\dfrac{30}{(r+2)}[/latex]:

[latex](r-2)\left(8-\dfrac{30}{(r+2)}\right)=30[/latex]

Multiply both sides by [latex](r + 2)[/latex] to eliminate the fraction, which leaves us with:

[latex](r-2)(8(r+2)-30)=30(r+2)[/latex]

[latex]\begin{array}{rrrrrrrrrrr} (r&-&2)(8r&+&16&-&30)&=&30r&+&60 \\ &&(r&-&2)(8r&+&(-14))&=&30r&+&60 \\ 8r^2&-&14r&-&16r&+&28&=&30r&+&60 \\ &&8r^2&-&30r&+&28&=&30r&+&60 \\ &&&-&30r&-&60&&-30r&-&60 \\ \hline &&8r^2&-&60r&-&32&=&0&& \end{array}[/latex]

This equation can be reduced by a common factor of 4, which will leave us:

[latex]\begin{array}{rll} 2r^2-15r-8&=&0 \\ (2r+1)(r-8)&=&0 \\ r&=&-\dfrac{1}{2}\text{ km/h (reject) or }r=8\text{ km/h} \end{array}[/latex]

For Questions 13 to 20, write and solve the equation describing the relationship.

• A train travelled 240 km at a certain speed. When the engine was replaced by an improved model, the speed was increased by 20 km/hr and the travel time for the trip was decreased by 1 hr. What was the rate of each engine?
• Mr. Jones visits his grandmother, who lives 100 km away, on a regular basis. Recently, a new freeway has opened up, and although the freeway route is 120 km, he can drive 20 km/h faster on average and takes 30 minutes less time to make the trip. What is Mr. Jones’s rate on both the old route and on the freeway?
• If a cyclist had travelled 5 km/h faster, she would have needed 1.5 hr less time to travel 150 km. Find the speed of the cyclist.
• By going 15 km per hr faster, a transit bus would have required 1 hr less to travel 180 km. What was the average speed of this bus?
• A cyclist rides to a cabin 72 km away up the valley and then returns in 9 hr. His speed returning is 12 km/h faster than his speed in going. Find his speed both going and returning.
• A cyclist made a trip of 120 km and then returned in 7 hr. Returning, the rate increased 10 km/h. Find the speed of this cyclist travelling each way.
• The distance between two bus stations is 240 km. If the speed of a bus increases by 36 km/h, the trip would take 1.5 hour less. What is the usual speed of the bus?
• A pilot flew at a constant speed for 600 km. Returning the next day, the pilot flew against a headwind of 50 km/h to return to his starting point. If the plane was in the air for a total of 7 hours, what was the average speed of this plane?

Example 10.7.6

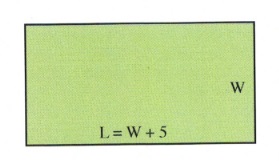
Find the length and width of a rectangle whose length is 5 cm longer than its width and whose area is 50 cm 2 .

First, the area of this rectangle is given by [latex]L\times W[/latex], meaning that, for this rectangle, [latex]L\times W=50[/latex], or [latex](W+5)W=50[/latex].

Multiplying this out gives us:

[latex]W^2+5W=50[/latex]

[latex]W^2+5W-50=0[/latex]

Second, we factor this quadratic to get our solution:

[latex]\begin{array}{rrrrrrl} W^2&+&5W&-&50&=&0 \\ (W&-&5)(W&+&10)&=&0 \\ &&&&W&=&5, -10 \\ \end{array}[/latex]

We reject the solution [latex]W = -10[/latex].

This means that [latex]L = W + 5 = 5+5= 10[/latex].

Example 10.7.7

If the length of each side of a square is increased by 6, the area is multiplied by 16. Find the length of one side of the original square.

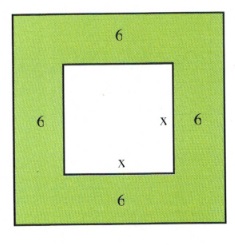
The relationship between these two is:

[latex]\begin{array}{rrl} \text{larger area}&=&16\text{ times the smaller area} \\ (x+12)^2&=&16(x)^2 \end{array}[/latex]

Simplifying this yields:

[latex]\begin{array}{rrrrrrr} x^2&+&24x&+&144&=&16x^2 \\ -16x^2&&&&&&-16x^2 \\ \hline -15x^2&+&24x&+&144&=&0 \end{array}[/latex]

Since this is a problem that requires factoring, it is easiest to use the quadratic equation:

[latex]x=\dfrac{-b\pm \sqrt{b^2-4ac}}{2a},\hspace{0.25in}\text{ where }a=-15, b=24\text{ and }c=144[/latex]

Substituting these values in yields [latex]x = 4[/latex] or [latex]x=-2.4[/latex] (reject).

Example 10.7.8

Nick and Chloe want to surround their 60 by 80 cm wedding photo with matting of equal width. The resulting photo and matting is to be covered by a 1 m 2 sheet of expensive archival glass. Find the width of the matting.

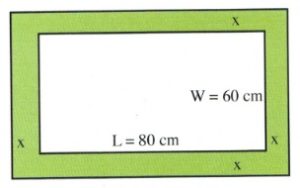
[latex](L+2x)(W+2x)=1\text{ m}^2[/latex]

[latex](80\text{ cm }+2x)(60\text{ cm }+2x)=10,000\text{ cm}^2[/latex]

[latex]4800+280x+4x^2=10,000[/latex]

[latex]4x^2+280x-5200=0[/latex]

Which reduces to:

[latex]x^2 + 70x - 1300 = 0[/latex]

Second, we factor this quadratic to get our solution.

It is easiest to use the quadratic equation to find our solutions.

[latex]x=\dfrac{-b\pm \sqrt{b^2-4ac}}{2a},\hspace{0.25in}\text{ where }a=1, b=70\text{ and }c=-1300[/latex]

Substituting the values in yields:

[latex]x=\dfrac{-70\pm \sqrt{70^2-4(1)(-1300)}}{2(1)}\hspace{0.5in}x=\dfrac{-70\pm 10\sqrt{101}}{2}[/latex]

[latex]x=-35+5\sqrt{101}\hspace{0.75in} x=-35-5\sqrt{101}\text{ (rejected)}[/latex]

For Questions 21 to 28, write and solve the equation describing the relationship.

• Find the length and width of a rectangle whose length is 4 cm longer than its width and whose area is 60 cm 2 .
• Find the length and width of a rectangle whose width is 10 cm shorter than its length and whose area is 200 cm 2 .
• A large rectangular garden in a park is 120 m wide and 150 m long. A contractor is called in to add a brick walkway to surround this garden. If the area of the walkway is 2800 m 2 , how wide is the walkway?
• A park swimming pool is 10 m wide and 25 m long. A pool cover is purchased to cover the pool, overlapping all 4 sides by the same width. If the covered area outside the pool is 74 m 2 , how wide is the overlap area?
• In a landscape plan, a rectangular flowerbed is designed to be 4 m longer than it is wide. If 60 m 2 are needed for the plants in the bed, what should the dimensions of the rectangular bed be?
• If the side of a square is increased by 5 units, the area is increased by 4 square units. Find the length of the sides of the original square.
• A rectangular lot is 20 m longer than it is wide and its area is 2400 m 2 . Find the dimensions of the lot.
• The length of a room is 8 m greater than its width. If both the length and the width are increased by 2 m, the area increases by 60 m 2 . Find the dimensions of the room.

Answer Key 10.7

Intermediate Algebra Copyright © 2020 by Terrance Berg is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License , except where otherwise noted.

Share This Book

• EXPLORE Random Article

How to Solve Word Problems Requiring Quadratic Equations

Last Updated: December 27, 2020

wikiHow is a “wiki,” similar to Wikipedia, which means that many of our articles are co-written by multiple authors. To create this article, volunteer authors worked to edit and improve it over time. This article has been viewed 14,258 times.

Some word problems require quadratic equations in order to be solved. In this article, you will learn how to solve those types of problems. Once you get the hang of it, it will be very easy.

Quadratic Equations

• For the real life scenarios, factoring method is better.
• In geometric problems, it is good to use the quadratic formula.

Real Life Scenario

• In this problem, it asks for Kenny's birthday.

• Since negative month does not exist, 3 is the only one that makes sense.
• Because the problem asks for both the month and the date, the answer would be March 18th. (Use the value for the other variable that you found in step 3.)

Geometric Problems

• In the problem above, it asks you only for the height of the triangle.

Expert Q&A

You might also like.

About this article

Did this article help you.

• About wikiHow
• Terms of Use
• Privacy Policy
• Do Not Sell or Share My Info
• Not Selling Info

To make full use of our website, Switch or update for free to one of the following current browsers:

Firefox , Google Chrome oder Internet Explorer 8 and above

To make full use of our website, enable JavaScript in your browser.

Our tutorial videos allow students to learn at their own pace without any pressure or stress. They can watch, pause or rewind the videos as often as they need until they understand the content.

Our interactive exercises come in a variety of formats so students can practice in a playful way. They get feedback and hints while solving the exercises. As a result, they learn and grow from their mistakes instead of feeling frustrated.

Children in elementary school can use Sofahero to review independently and stay motivated. They master topics while going on exciting adventures, without the help of adults.

Students can use the worksheets to prepare themselves for mock tests: Simply print them out, fill them out, and check the answers using the answer key.

Real teachers provide students with fast, personalized support. They can help walk students through homework problems, review lessons, and answer questions in an easy-to-understand way.

With interactive e-books children can playfully train their active listening and comprehension skills.

Cancel at any time

Discover why over 1.6 MILLION students choose sofatutor!

• Quadratic Equations / Functions

Word Problems with Quadratic Equations

Watch videos

Start exercises

Show worksheets

Unlock this video in just a few steps, and benefit from all sofatutor content

Videos for all grades and subjects that explain school material in a short and concise way.

Boost your confidence in class by studying before tests and mock tests with our fun exercises.

Learn on the go with worksheets to print out – combined with the accompanying videos, these worksheets create a complete learning unit.

24-hour help provided by teachers who are always there to assist when you need it.

You must be logged in to be able to give a rating.

Wow, thank you! Please rate us on Google too! We look forward to it!

Basics on the topic Word Problems with Quadratic Equations

There are many ways to solve quadratic equations. You can factor them, complete the square, graph them, and use the quadratic formula, for instance.

At least one of these methods can be used to solve any problem involving a quadratic equation, and which method you choose depends on the kind of problem you are presented with.

If the quadratic equation can be represented by mapping or a table, then graphing can do the trick. If the quadratic equation is factorable, then factoring, of course, and completing the square are good choices. When the quadratic equation has coefficients that are real numbers, like decimals, fractions, or maybe even radicals, then using the quadratic formula is highly recommended.

One must note though that these problems often look for concrete answers, like units of measurement or quantity. A negative root, though a valid solution to a quadratic equation, may not be the answer that a word problem is looking for. A positive root, or possibly roots, then is the more appropriate final answer.

Analyze Functions Using Different Representations.

CCSS.MATH.CONTENT.HSF.IF.C.8.A

Transcript Word Problems with Quadratic Equations

The mighty King Wallace sits on his throne and rules his kingdom every day of the year, except for his birthday. Every year, to celebrate his birthday he takes a trip to visit various scenic outlooks and famous locations within his kingdom. For this year’s birthday celebration, the decision is difficult, there're so many destinations to choose from.But finally, the mighty king decides to visit one of the more beautiful castles in his kingdom for the umteenth time. To prepare for the king's visit, the servants must cover the ground around the castle with carpet, so the King’s shoes won’t get dirty. How much carpet do they need?

Setting up the quadratic equation

To figure this out, we can use a quadratic equation . Take a look at the diagram of the castle. The length of the area that needs carpet is equal to an unknown length, 'x', plus 9, the width is 'x' + 3, and the total area is 72 square wallacesons. You might be wondering, what’s a wallaceson? King Wallace devised his very own system of weights and measures. I know! What a narcissist but whatever, right?! Okay back to the problem. To help the servants figure out the amount of carpet they need, we can set up an equation and solve for 'x' . First use FOIL : first, outer, inner, last. You know the drill.

Factoring the quadratic equation

Next, you'll need to factor the quadratic equation. Using the standard form of the quadratic equation as your guide, set the equation equal to zero . Then find the product of ac that sums to 'b'. That's negative 3 and 15. Now set each of the two binomials factors equal to 0. You're not done yet; you still have to solve for 'x'. Use opposite operations to solve each mini equation. X has two possible solutions, 3 and negative 15.

Completing the square

But factoring’s not the only game in town. We can also solve for 'x' by completing the square . FOIL first , so it's easier to work with. To complete the square, follow these steps: Move the constant to the other side of the equal sign . Then take the 'b' value , divide it by 2, and square it, and then add this number to both sides of the equation. Factor the left side of the equal sign and finally, solve for 'x' , by taking the square root of each side of the equal sign and finish it off with PEMDAS . X is equal to 3 and -15, just like before.

Let’s plug in the values for 'x' into the equation, so the servants can order the carpet. Plug in 'x' is equal to 3. The measurements are 12 wallacesons by 6 wallacesons! That’s a big carpet! Now for the second value, 'x' = -15. The measurements of the carpet are equal to -6 and -12. You can’t have a negative measure of carpet so although 'x' = -15 works as a solution for the quadratic equation. It’s not a valid solution for this situation. So the correct solution is 'x' is equal to 3.

Indecisive as always, the king changes his mind at the very last minute and decides he wants to visit a place he’s never been to before. He'll go to a village near the border of his kingdom. He’s been curious about this village because he heard they have some unusual customs. When the King gets to the village, the villagers seem normal enough. The villagers stand with baskets of apples patiently waiting for his speech to begin. Luckily for the king, his squire knows all about the village's unusual customs, the villagers always give an enthusiastic welcome to visitors. By throwing apples at them! To keep the king safe, the squire will have to control the crowd, but how can he do that?

Graphing the parabola

The king will give his speech while standing on a tower 5 wallace yards high, at the point on the graph (0, 5). The trajectory of the apples can be described by the function of 'x' = -0.25x² + 2x + 5, since it's a quadratic equation, we know the shape of the graph is a parabola . So, where does the crowd need to stand to so they won't be able to hit the king with apples? This whole situation sounds a little crazy, right? What can you do? You have to respect peoples' customs, right?

Let’s solve this problem by graphing . Plug in a few points for 'x' and determine the corresponding 'y' values . Plot the points and then draw in the parabola . Where the graph touches the x-axis is a possible solution set for this quadratic equation, at 'x' = 10 and -2. The king will be safe as long as the crowd is placed more than 10 feet in front of the podium or 2 feet behind.

Quadratic formula

We can also calculate the solution by using the quadratic formula. Use the standard quadratic equation as your guide to determine the values for a, b, and c, but first manipulate the equation so the 'a' value is equal to positive 1. You could skip this step, but it makes the numbers easier to work with. Now substitute the 'a', 'b' and 'c' values into the quadratic formula, and then do the math. The answer is the same as before, 'x' is equal to 10 and -2. Just as the squire expected, the crowd welcomed the king by throwing lots of apples but thanks to the quadratic equation, the king gave his speech without a single apple finding its mark.

Word Problems with Quadratic Equations exercise

Explain how to solve a quadratic equation by factoring..

• multiply the F irst $x^2$
• multiply the O uter $9x$
• multiply the I nner $3x$
• multiply the L asr $27$

Here is an example for solving an equation; subtraction is the opposite operation of addition.

Use the zero factor property: if a product is equal to zero then one of its factors must also be equal to zero.

The servants have to calculate the total length of the carpet.

To do this they first use the FOIL method for multiplying the two binomials:

$(x+9)(x+3)=x^2+9x+3x+27=x^2+12x+27$.

This quadratic term is equal to the given total area. So we get

$x^2+12x+27=72$,

which is equivalent to

$\begin{array}{rcl} x^2+12x+27&=&~72\\ \color{#669900}{-72} & &\color{#669900}{-72}\\ x^2+12x-45&=&~0. \end{array}$

• $1\times(-45)=-45$ but $1-45=-44$
• $3\times (-15)=-45$ but $3-15=-12$
• $-3\times 15=-45$ and $-3+15=12$ $~~~~~$✓

To get the solutions we use opposite operations twice:

$\begin{array}{rcl} x-3&=&~0\\ \color{#669900}{+3} & &\color{#669900}{+3}\\ x&=&~3 \end{array}$

$\begin{array}{rcl} x+15&=&~0\\ \color{#669900}{-15} & &\color{#669900}{-15}\\ x&=&~-15 \end{array}$

For $x=3$ we get that the length is $3+9=12$ and the width is $3+3=6$. And for $x=-15$, the length is $-15+9=-6$ ... so we can stop because there don't exist any negative lengths.

This means that both $x=3$ as well as $x=-15$ are solutions to the quadratic equation, but only $x=3$ is a possible solution in our given situation.

Determine how to solve quadratic equations graphically.

The function above is a quadratic function.

Any linear function is given by $f(x)=mx+b$, where $m$ is the slope and $b$ the $y$-intercept. The graph of such a function is a line.

The graph of a quadratic function is a parabola. Each parabola has at most two $x$-intercepts.

There exist different ways to solve quadratic equations like $ax^2+bx+c=0$.

For example, lets draw the parabola in a coordinate plane which corresponds to the graph of

• Plug in a few values for $x$ and calculate the corresponding $y$-values.
• Plot the resulting ordered pairs $(x,y)$ in a coordinate plane.
• Connect those pairs to get the corresponding parabola.

Determine how to solve quadratic equations by completing the square.

• multiply the O uter $-3x$
• multiply the I nner $2x$
• multiply the L asr $-6$

To complete a quadratic term $x^2+bx$ add $\left(\frac b2\right)^2$.

Here is an example for solving an equation by taking a square root.

Don't forget the $\pm$ sign in your calculation!

Check the solutions. Do they makes sense when trying to determine the positive length and width of the moat?

First we use the FOIL method for multiplying the two binomials

$(x+2)(x-3)=x^2-3x+2x-6=x^2-x-6$.

This must be equal to the given total area. So we get $x^2-x-6=50$, which is equivalent to

$\begin{array}{rcl} x^2-x-6&=&~50\\ \color{#669900}{+6} & &\color{#669900}{+6}\\ x^2-x&=&~56 \end{array}$

Now we complete the quadratic term on the left-hand side to a square. For this we add $(\frac12)^2$:

$\begin{array}{rcl} x^2-x&=&~56\\ \color{#669900}{+\left(\frac12\right)^2} & &\color{#669900}{+\left(\frac12\right)^2}\\ x^2-x+\left(\frac12\right)^2&=&~56+\left(\frac12\right)^2\\ \left(x-\frac12\right)^2&=&~56.25 \end{array}$

Next we take the square root of both sides to get

$x-\frac12=\pm7.5$.

Lastly we add $\frac12=0.5$, which leads to the desired solutions

$x=0.5+7.5=8$ or $x=0.5-7.5=-7$.

Let's check if both solutions work with the problem at hand, keeping in mind that we are trying to find the length and width of a moat.

For $x=8$ we get the length $8+2=10$ and the width $8-3=5$. Both are positive, so this solution works.

For $x=-7$ we get the length $-7+2=-5$ and the width $-7-3=-10$. A negative length and width doesn't make any sense, so this solution can't work in our given situation.

Calculate where the castle ditches have to be built by using the quadratic formula.

You can also multiply the equation $-0.5x^2-1.5x+5=0$ by $-2$ to get $x^2+3x-10=0$.

Both solutions are whole numbers. One is negative and the other one is positive.

You can solve each quadratic equation $ax^2+bx+c=0$ by using the quadratic formula,

$x=\frac{-b \pm\sqrt{b^2-4ac}}{2a}$.

First determine $a$, $b$ and $c$ in the equation and then plug those values into the quadratic formula.

For $-0.5x^2-1.5x+5=0$, we have that $a=-0.5$, $b=-1.5$, and $c=5$.

So we calculate

$\begin{array}{rcl} x&=&\frac{1.5\pm\sqrt{(-1.5)^2-4(-0.5)(5)}}{2(-0.5)}\\ &=&~\frac{1.5\pm\sqrt{2.25+10}}{-1}\\ &=&~-1.5\pm\sqrt{12.25}\\ x_1&=&~-1.5+3.5=2\\ x_2&=&~-1.5-3.5=-5 \end{array}$

The desired solutions are then $x=2$ or $x=-5$.

Perhaps you'd like to multiply the quadratic equation $-0.5x^2-1.5x+5=0$ with $-2$ to get $x^2+3x-10=0$. You don't have to do it but it makes the calculations a little bit less complicated.

Name the methods for solving quadratic equations.

The solutions of the corresponding quadratic equation are $x=10$ and $x=90$.

This is the quadratic formula.

The zero factor property states that if a product is equal to zero then one of its factors must also equal zero.

It doesn't matter at all which method you choose to find the solutions. If the solutions exist, then they are always the same.

• You could factor the left-hand side of the equation $x^2+bx+c=0$ to $(x+d)(x+e)=0$ and get the solutions $x=-d$ and $x=-e$.
• You can complete the square to get $(x+e)^2=d$. You can solve this equation by taking the square root of both sides.
• You can use the quadratic formula for solving $ax^2+bx+c=0$.
• You also could draw the parabola corresponding to $f(x)=ax^2+bx+c$. The $x$-intercepts of this parabola are the desired solutions.

Solve the following quadratic equations.

Decide which method you you like to use. No matter which method you choose, your results will always be the same.

Here you see the quadratic formula for solving quadratic equations like $ax^2+bx+c=0$.

For solving a quadratic equation $x^2+bx+c=0$ by factoring, find the factors of $c$ which sum to $b$.

Here is an example of complete the square of a quadratic equation.

Let's solve the various quadratic equations using the different methods we learned:

• Look for the factors of $8$ which sum to $-2$, namely $2\times (-4)=-8$ and $2-4=-2$ $~~~~~$✓.
• Thus we get the equivalent equation $(x+2)(x-4)=0$ which we solve by using opposite operations:

$\begin{array}{rcl} x+2&=&~0\\ \color{#669900}{-2} & &\color{#669900}{-2}\\ x&=&~-2 \end{array}$

$\begin{array}{rcl} x-4&=&~0\\ \color{#669900}{+4} & &\color{#669900}{+4}\\ x&=&~4 \end{array}$

This method (better!) works for whole solutions.

• Subtract $7$ from both sides to get $x^2-8x=-7$.
• Adding $4^2$ on both sides leads to $x^2-8x+4^2=-7+4^2$.
• $(x-4)^2=9$ is the resulting equation.
• Take the square root on both sides and don't forget the $\pm$ sign: $x-4=\pm3$.
• Almost done: add $4$ to get $x=4+3=7$ or $x=4-3=1$.

You can also use the quadratic formula , which we will use to solve $2x^2+4x-6=0$. Nothing that $a=2$, $b=4$, and $c=-6$, we have that

$\begin{array}{rcl} x&=&~\frac{-4\pm\sqrt{(-4)^2-4(2)(-6)}}{2(2)}\\ &=&~\frac{-4\pm\sqrt{16+48}}{4}\\ &=&~\frac{-4\pm\sqrt{64}}{4}\\ x_1&=&~\frac{-4+8}{4}=1\\ x_2&=&~\frac{-4-8}{4}=-3 \end{array}$

For $0.2x^2+1.2x+1=0$, first multiply both sides of the equation by $5$ to get $x^2+6x+5=0$, and thus $a=1$, $b=6$ and $c=5$. This simplifies the following calculation:

$\begin{array}{rcl} x&=&~\frac{-6\pm\sqrt{6^2-4(1)(5)}}{2(1)}\\ &=&~\frac{-6\pm\sqrt{36-20}}{2}\\ &=&~\frac{-6\pm\sqrt{16}}{2}\\ x_1&=&~\frac{-6+4}{2}=-1\\ x_2&=&~\frac{-6-4}{2}=-5 \end{array}$

What are Quadratic Functions?

Graphing Quadratic Functions

FOILing and Explanation for FOIL

Solving Quadratic Equations by Taking Square Roots

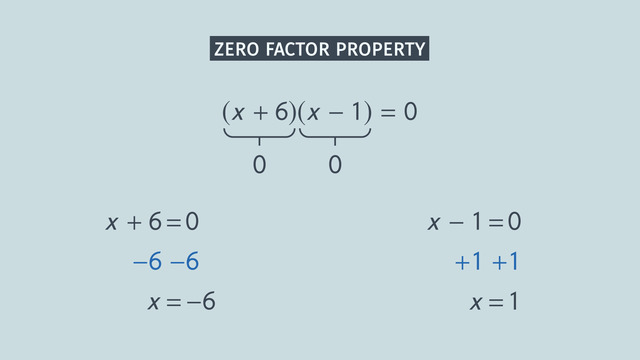
Solving Quadratic Equations by Factoring

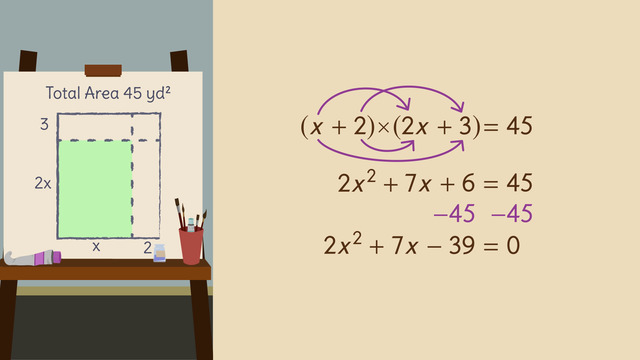
Factoring with Grouping

Solving Quadratic Equations Using the Quadratic Formula

Solving Quadratic Equations by Completing the Square

Finding the Value that Completes the Square

Using and Understanding the Discriminant

• Proven learning success
• Gamification
• Tutorial Videos
• Interactive books
• Give Us Feedback
• Terms & Conditions
• Privacy Policy
• Do Not Sell My Personal Information

We are using cookies and various third-party services to optimize our platform for you, to continually improve our content and offerings for you and to measure and manage our advertising. You can find detailed information in our privacy policy .

You can accept all cookies and embedded services or choose in the setting, which cookies you want to accept.

Cookies that are necessary for delivering our services or for using our website can’t be rejected.

To provide additional functionality on our platform and to continually optimize our website, we are using our own cookies and third-party services, for example Olark, Hotjar, Userlane and Amplitude.

For the analysis and optimization of our platform, our content and our offerings, we are using our own cookies as well as various third-party services, for example Google Analytics.

For measuring and controlling our marketing and managing our advertising, we are using our own cookies as well as various third-party services, for example Google Adwords/Doubleclick, Bing, Youtube, Facebook, TikTok, Pinterest, LinkedIn, Taboola and Outbrain.

HOW TO SOLVE WORD PROBLEMS IN QUADRATIC EQUATIONS

We can follow the steps given below to solve word problems using quadratic equations.

Understanding the question is more important than any other thing. That is, always it is very important to understand the information given in the question rather than solving.

If it is possible, we have to split the given information. Because, when we split the given information in to parts, we can understand them easily.

Once we understand the given information clearly, solving the word problem in quadratic equation would not be a challenging work. 

When we try to solve the word problems in quadratic equations, we have to introduce "x" or some other alphabet for unknown value (=answer for our question) and form a quadratic equation with this "x". Finally we have to get value for the alphabet which was introduced for the unknown value.

If it is required, we have to draw picture for the given information. Drawing picture for the given information will give us a clear understanding about the question.

Using the alphabet introduced for unknown value, we have to translate the English statement (information) given in the question as quadratic equation equation.

In translation, we have to translate  the following English words as the corresponding mathematical symbols.

of -----> x (multiplication)

am, is, are, was, were, will be, would be --------> = (equal)

Once we have translated the English Statement (information) given in the question as quadratic equation correctly, 90% of the work will be over. The remaining 10% is just getting the answer. That is solving for the unknown. 

These are the steps most commonly involved in solving word problems in quadratic equations.

Let us see how the above explained steps work in solving word problems using quadratic equations. 

A piece of iron rod cost $ 60. If the rod was 2 meter shorter and each meter costs $ 1 more and the total cost  would remain unchanged. What is the length of the rod?  

Let us understand the given information. There are three information given in the question. 

1.  A piece of iron rod costs $ 60.

2.  If the rod was 2 meter shorter and each meter costs $ 1 more

3.  Total cost  would remain unchanged.

Target of the question : What is the length of the rod?

Step 3 :

Let "x" be the length of the rod.

Clearly, we have to find the value of "x" 

If the rod is 2 meter shorter, length of the rod is

=  (x-2)

From the third information, we have the following statements.

Total cost of rod having length x meters is $ 60.

Total cost of rod having length (x-2) meters is $ 60.

Cost of 1 meter of rod having length x meters is

=  60 / x  -----(1)

Cost of 1 meter of rod having length (x-2) meters is

=  60 / (x - 2) -----(2)

From the second information, we can consider the following example. 

That is, if the cost of 1 meter of rod x is $10, then the cost of 1 meter of rod (x-2) will be $11.  

$10 &  $11 can be balanced as shown below.

10 + 1  =  11

(This is just for en example)

If we apply the same logic for (1) & (2), we get 

(60 / x) + 1  =  60 / (x - 2)

(60 + x) / x  =  60 / (x - 2)

(x + 60)(x - 2)  =  60x

x 2  + 58x - 120  =  60x

x 2  - 2x - 120  =  0

(x - 12)(x + 10)  =  0 

x - 12  =  0     or     x + 10  =  0

x  =  12     or     x  =  -10

Because length can never be a negative value, we can ignore x  =  -10. 

x  =  12

So, the length of the rod is 12 meter. 

Would you like to practice more word problems in quadratic equations ? 

Please click here

Kindly mail your feedback to   [email protected]

We always appreciate your feedback.

© All rights reserved. onlinemath4all.com

• Sat Math Practice
• SAT Math Worksheets
• PEMDAS Rule
• BODMAS rule
• GEMDAS Order of Operations
• Math Calculators
• Transformations of Functions
• Order of rotational symmetry
• Lines of symmetry
• Compound Angles
• Quantitative Aptitude Tricks
• Trigonometric ratio table
• Word Problems
• Times Table Shortcuts
• 10th CBSE solution
• PSAT Math Preparation
• Privacy Policy
• Laws of Exponents

Recent Articles

Honors Algebra 2 Problems on Solving Exponential Equations

Mar 30, 24 11:45 PM

Properties of Parallelograms Worksheet

Mar 30, 24 09:11 PM

Division by Zero

Mar 30, 24 08:11 AM

Word Problems on Quadratic Equations by Factoring

We will learn how to solve Word Problems on quadratic equations by factoring.

1.  The product of two numbers is 12. If their sum added to the sum of their squares is 32, find the numbers.

Let the numbers be x and y.

As their product is 12, we get xy = 12 ..................... (i)

According to the question, x + y + x\(^{2}\) + y\(^{2}\) = 32 ..................... (ii)

From (i), y = \(\frac{12}{x}\)

Putting y = \(\frac{12}{x}\) in (ii), we get

x + \(\frac{12}{x}\) + x\(^{2}\) + (\(\frac{12}{x}\))\(^{2}\) = 32

⟹ (x + \(\frac{12}{x}\)) + (x + \(\frac{12}{x}\))\(^{2}\) - 2 x ∙ \(\frac{12}{x}\) = 32

⟹ (x + \(\frac{12}{x}\))\(^{2}\) + (x + \(\frac{12}{x}\)) - 56 = 0

Putting x + \(\frac{12}{x}\) = t,

t\(^{2}\) + t - 56 = 0

⟹ t\(^{2}\) + 8t – 7t – 56 = 0

⟹ t(t + 8) - 7(t + 8) = 0

⟹ (t + 8)(t - 7) = 0

⟹ t + 8 = 0 or, t – 7 = 0

⟹ t = -8 or, t = 7

When t = -8,

x + \(\frac{12}{x}\) = t = -8

⟹ x\(^{2}\) + 8x + 12 = 0

⟹ x\(^{2}\) + 6x + 2x + 12 = 0

⟹ x(x + 6) + 2(x + 6) = 0

⟹ (x + 6)(x + 2) = 0

⟹ x + 6 = 0 or, x + 2 = 0

⟹ x = -6 or, x = -2

x + \(\frac{12}{x}\) = t = 7

⟹ x\(^{2}\) - 7x + 12 = 0

⟹ x\(^{2}\) - 4x - 3x + 12 = 0

⟹ x(x – 4) - 3(x – 4) = 0

⟹ (x - 4)(x - 3) = 0

⟹ x - 4 = 0 or, x - 3 = 0

⟹ x = 4 or 3

Thus, x = -6, -2, 4, 3

Then, the other number y = \(\frac{12}{x}\) = \(\frac{12}{-6}\) , \(\frac{12}{-2}\), \(\frac{12}{4}\), \(\frac{12}{3}\) = -2, -6, 3, 4.

Thus, the two numbers x, y are -6, -2, or -2, -6, or 4, 3 or 3, 4.

Therefore, the required two numbers are -6, -2 or 4, 3.

2. An association has a fund of $195. In addition that, each member of the association contributes the number of dollars equal to the number of members. The total money is divided equally among the members. If each of the members gets $ 28, find the number of members in the association.

Let the number of members be x.

Total contributions from them = $ x\(^{2}\) and the association has a fund of $ 195.

According to the problem,

x\(^{2}\)  + 195 = 28x

⟹ x\(^{2}\)  - 28x + 195 = 0

⟹ x\(^{2}\) - 15x - 13x + 195 = 0

⟹ x(x - 15) - 13(x - 15) = 0

⟹ (x - 15)(x - 13) = 0

Therefore, x = 15 or 13

There are 15 or 13 members in the association.

Note: Two answers are acceptable in this case.

Quadratic Equation

Introduction to Quadratic Equation

Formation of Quadratic Equation in One Variable

Solving Quadratic Equations

General Properties of Quadratic Equation

Methods of Solving Quadratic Equations

Roots of a Quadratic Equation

Examine the Roots of a Quadratic Equation

Problems on Quadratic Equations

Quadratic Equations by Factoring

Word Problems Using Quadratic Formula

Examples on Quadratic Equations 

Worksheet on Formation of Quadratic Equation in One Variable

Worksheet on Quadratic Formula

Worksheet on Nature of the Roots of a Quadratic Equation

Worksheet on Word Problems on Quadratic Equations by Factoring

• 9th Grade Math

From Word Problems on Quadratic Equations by Factoring to HOME PAGE

New! Comments

Didn't find what you were looking for? Or want to know more information about Math Only Math . Use this Google Search to find what you need.

• Preschool Activities
• Kindergarten Math
• 1st Grade Math
• 2nd Grade Math
• 3rd Grade Math
• 4th Grade Math
• 5th Grade Math
• 6th Grade Math
• 7th Grade Math
• 8th Grade Math
• 10th Grade Math
• 11 & 12 Grade Math
• Concepts of Sets
• Probability
• Boolean Algebra
• Math Coloring Pages
• Multiplication Table
• Cool Maths Games
• Math Flash Cards
• Online Math Quiz
• Math Puzzles
• Binary System
• Math Dictionary
• Conversion Chart
• Homework Sheets
• Math Problem Ans
• Free Math Answers
• Printable Math Sheet
• Funny Math Answers
• Employment Test
• Math Patterns
• Link Partners
• Privacy Policy

Recent Articles

Word Problems on Multiplication |Multiplication Word Problem Worksheet

Mar 31, 24 11:21 AM

Multiplication by Ten, Hundred and Thousand |Multiply by 10, 100 &1000

Mar 31, 24 10:09 AM

Properties of Multiplication | Multiplicative Identity | Whole Numbers

Mar 29, 24 05:08 PM

Multiplication of a Number by a 3-Digit Number |3-Digit Multiplication

Mar 28, 24 06:33 PM

Solver Title

Generating PDF...

• Pre Algebra Order of Operations Factors & Primes Fractions Long Arithmetic Decimals Exponents & Radicals Ratios & Proportions Percent Modulo Number Line Mean, Median & Mode
• Algebra Equations Inequalities System of Equations System of Inequalities Basic Operations Algebraic Properties Partial Fractions Polynomials Rational Expressions Sequences Power Sums Interval Notation Pi (Product) Notation Induction Logical Sets Word Problems
• Pre Calculus Equations Inequalities Scientific Calculator Scientific Notation Arithmetics Complex Numbers Polar/Cartesian Simultaneous Equations System of Inequalities Polynomials Rationales Functions Arithmetic & Comp. Coordinate Geometry Plane Geometry Solid Geometry Conic Sections Trigonometry
• Calculus Derivatives Derivative Applications Limits Integrals Integral Applications Integral Approximation Series ODE Multivariable Calculus Laplace Transform Taylor/Maclaurin Series Fourier Series Fourier Transform
• Functions Line Equations Functions Arithmetic & Comp. Conic Sections Transformation
• Linear Algebra Matrices Vectors
• Trigonometry Identities Proving Identities Trig Equations Trig Inequalities Evaluate Functions Simplify
• Statistics Mean Geometric Mean Quadratic Mean Average Median Mode Order Minimum Maximum Probability Mid-Range Range Standard Deviation Variance Lower Quartile Upper Quartile Interquartile Range Midhinge Standard Normal Distribution
• Physics Mechanics
• Chemistry Chemical Reactions Chemical Properties
• Finance Simple Interest Compound Interest Present Value Future Value
• Economics Point of Diminishing Return
• Conversions Roman Numerals Radical to Exponent Exponent to Radical To Fraction To Decimal To Mixed Number To Improper Fraction Radians to Degrees Degrees to Radians Hexadecimal Scientific Notation Distance Weight Time Volume
• Pre Algebra
• One-Step Addition
• One-Step Subtraction
• One-Step Multiplication
• One-Step Division
• One-Step Decimals
• Two-Step Integers
• Two-Step Add/Subtract
• Two-Step Multiply/Divide
• Two-Step Fractions
• Two-Step Decimals
• Multi-Step Integers
• Multi-Step with Parentheses
• Multi-Step Rational
• Multi-Step Fractions
• Multi-Step Decimals
• Solve by Factoring
• Completing the Square
• Quadratic Formula
• Biquadratic
• Logarithmic
• Exponential
• Rational Roots
• Floor/Ceiling
• Equation Given Roots
• Newton Raphson
• Substitution
• Elimination
• Cramer's Rule
• Gaussian Elimination
• System of Inequalities
• Perfect Squares
• Difference of Squares
• Difference of Cubes
• Sum of Cubes
• Polynomials
• Distributive Property
• FOIL method
• Perfect Cubes
• Binomial Expansion
• Negative Rule
• Product Rule
• Quotient Rule
• Expand Power Rule
• Fraction Exponent
• Exponent Rules
• Exponential Form
• Logarithmic Form
• Absolute Value
• Rational Number
• Powers of i
• Partial Fractions
• Is Polynomial
• Leading Coefficient
• Leading Term
• Standard Form
• Complete the Square
• Synthetic Division
• Linear Factors
• Rationalize Denominator
• Rationalize Numerator
• Identify Type
• Convergence
• Interval Notation
• Pi (Product) Notation
• Boolean Algebra
• Truth Table
• Mutual Exclusive
• Cardinality
• Caretesian Product
• Age Problems
• Distance Problems
• Cost Problems
• Investment Problems
• Number Problems
• Percent Problems
• Addition/Subtraction
• Multiplication/Division
• Dice Problems
• Coin Problems
• Card Problems
• Pre Calculus
• Linear Algebra
• Trigonometry
• Conversions

Most Used Actions

Number line.

• \mathrm{Lauren's\:age\:is\:half\:of\:Joe's\:age.\:Emma\:is\:four\:years\:older\:than\:Joe.\:The\:sum\:of\:Lauren,\:Emma,\:and\:Joe's\:age\:is\:54.\:How\:old\:is\:Joe?}
• \mathrm{Kira\:went\:for\:a\:drive\:in\:her\:new\:car.\:She\:drove\:for\:142.5\:miles\:at\:a\:speed\:of\:57\:mph.\:For\:how\:many\:hours\:did\:she\:drive?}
• \mathrm{The\:sum\:of\:two\:numbers\:is\:249\:.\:Twice\:the\:larger\:number\:plus\:three\:times\:the\:smaller\:number\:is\:591\:.\:Find\:the\:numbers.}
• \mathrm{If\:2\:tacos\:and\:3\:drinks\:cost\:12\:and\:3\:tacos\:and\:2\:drinks\:cost\:13\:how\:much\:does\:a\:taco\:cost?}
• \mathrm{You\:deposit\:3000\:in\:an\:account\:earning\:2\%\:interest\:compounded\:monthly.\:How\:much\:will\:you\:have\:in\:the\:account\:in\:15\:years?}
• How do you solve word problems?
• To solve word problems start by reading the problem carefully and understanding what it's asking. Try underlining or highlighting key information, such as numbers and key words that indicate what operation is needed to perform. Translate the problem into mathematical expressions or equations, and use the information and equations generated to solve for the answer.
• How do you identify word problems in math?
• Word problems in math can be identified by the use of language that describes a situation or scenario. Word problems often use words and phrases which indicate that performing calculations is needed to find a solution. Additionally, word problems will often include specific information such as numbers, measurements, and units that needed to be used to solve the problem.
• Is there a calculator that can solve word problems?
• Symbolab is the best calculator for solving a wide range of word problems, including age problems, distance problems, cost problems, investments problems, number problems, and percent problems.
• What is an age problem?
• An age problem is a type of word problem in math that involves calculating the age of one or more people at a specific point in time. These problems often use phrases such as 'x years ago,' 'in y years,' or 'y years later,' which indicate that the problem is related to time and age.

word-problems-calculator

• Middle School Math Solutions – Equation Calculator Welcome to our new "Getting Started" math solutions series. Over the next few weeks, we'll be showing how Symbolab...

Please add a message.

Message received. Thanks for the feedback.

If you're seeing this message, it means we're having trouble loading external resources on our website.

If you're behind a web filter, please make sure that the domains *.kastatic.org and *.kasandbox.org are unblocked.

To log in and use all the features of Khan Academy, please enable JavaScript in your browser.

Class 10 (Old)

Course: class 10 (old)   >   unit 4.

• Quadratic equations word problem: triangle dimensions
• Quadratic equations word problem: box dimensions
• Quadratic word problem: ball
• Word problems: Writing quadratic equations
• Word problems: Solving quadratic equations
• Quadratic equations word problems (basic)
• Quadratic equations word problems (intermediate)

Quadratic equations word problems (advanced)